关于一般q-李代数的普遍包络代数U(Lq)的研究

刘孝磊，李 沫，刘晓燕，马翠玲

（海军航空工程学院基础部，山东 烟台 264001）

随着在物理领域对李代数应用的深入，人们对这种代数结构的研究越来越广泛。随之出现了一些广义李代数如李超代数、τ -李代数、ε -李代数等，并在量子物理等很多领域得到了重要应用。

本文在李代数进行的另外一种拓展——q-李代数的基础上，对q-李代数所蕴含的深层的代数性质进行剖析，研究了一般q-李代数的普遍包络代数U(Lq)及其重要的代数性质，证明了普遍包络代数U(Lq)的PBW定理，并给出了 U(Lq)的一组基。

1 预备知识

首先引入普遍意义上的张量代数。

取定数域K 上的一个向量空间V，T0V=K，个)，定义：并且我们引入一个结合乘积：

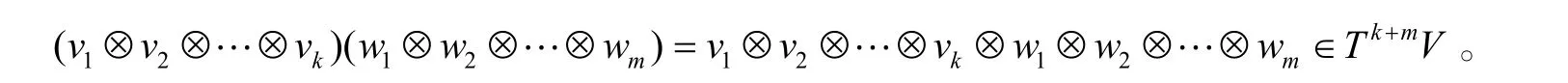
定义在T (V)的齐次生成元上，这使 T (V)成为一个含幺的结合阶化代数，它由1以及V的任意一组基所生成，我们称之为V 上的张量代数。

有了张量代数的定义后，再加上q-李代数Lq的定义，就可以把q-李代数Lq看成向量空间，从而对Lq也就有了它的张量代数T (Lq)。另外，我们还给出 Lq的一个双边理想 Jq，它是由元素：生成的，从而就可以定义商代数为q-李代数Lq的普遍包络代数，记为U(Lq)。

因为有嵌入映射 i∶Lq→T (Lq)以及典范映射π∶T (Lq) → T (Lq) Jq=U(Lq)，我们就可以把这两个映射合成起来，记为σ=π· i：Lq→U(Lq)，称σ为从q-李代数Lq到普遍包络代数U(Lq)的典范映射。

另外，

2 U(Lq)的泛性质及其PBW定理

首先给出 U(Lq)的泛性质。

定理假设σ为从q-李代数qL到普遍包络代数U(Lq)的典范映射，A为一个含幺的代数。进一步假设ϕ是一个从qL到A的线性映射，满足

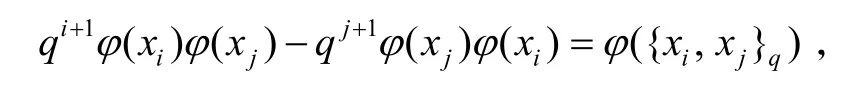
∀xi∈ Li，则存在惟一一个从 U(Lq)到A的同态ϕ/′，满足 ϕ/′(1)=1且ϕ ′·σ=ϕ。

证明：由定义知普遍包络代数U(Lq)能由1以及 σ(Lq)生成，从而得到ϕ/′是惟一的。

另一方面，由张量代数T (Lq)的泛性质，我们知道存在惟一的一个从 T (Lq)到A的同态，设为φ，它是ϕ的扩展，且φ (1)=1，对于 ∀xi∈ Li，有

因此 φ(Jq)=0，而通过作商的过程，φ就定义了一个从U(Lq)到A的同 态ϕ/′，满足 ϕ/′ (1)=1且ϕ ′·σ=ϕ.

注在U(Lq)中，李括积的双线性，可以这样来理解：

接下来我们寻找 U(Lq)的一组基。

首先固定qL的一组有序齐次基：满足 xik∈ Ln，其中n ∈ N。用{Lq}来表示包络代数T (Lq)中单项式的集合，并定义单项式 xj1⊗ xj2⊗ …⊗ xjn的一个(正)排序：当jl＜jk时，有 xjl＜xjk。我们给出{Lq}中2个多项式集合的一个偏序：B＜C是指B中的单项式长度比C 中的更短些，或者B中的单项式是C 中单项式的置换排序，但是要满足给出的正排序。显然，若B＜B′，则有 A⊗B⊗C＜A⊗B′⊗C，其中A,B,B ′,C∈{Lq}。

引理J (xi,xj,xk)∈。

证明：注意到在J (xi,xj,xk)表达式中的每一个单项式都＜xk⊗ xj⊗ xi。下面证明 J (xi,xj,xk) ∈ Jq。

由于

从而

故

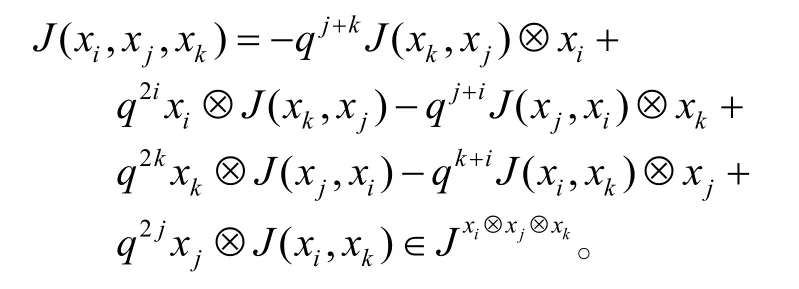
另外，对每个ς∈ S，我们用ϕς来表示 U(Lq)上的一个映射A ⊗ Wς⊗ C → A ⊗ fς⊗ C，在此映射中，不包含Wς的那些多项式不变。记 ϕS={ϕς|ς ∈ S}。

定理(q-PBW)

证明：令

因为{,}q是反对称的，并且是双线性的，所以由 Wςxy−fςxy生成的理想恰好是前面定义的

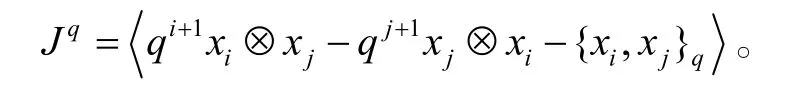
又由于每个 ϕς把A ⊗ Wς⊗ C 映成A ⊗ fς⊗ C。所以在ϕς的作用下，对某个固定的单项式在U(Lq)中的像也恰好是所对应的基。

当给出 xi,xj,xk满足 xi＜xj＜xk时，利用上面所定义的映射去作用之后，将最终落在下面我们来计算

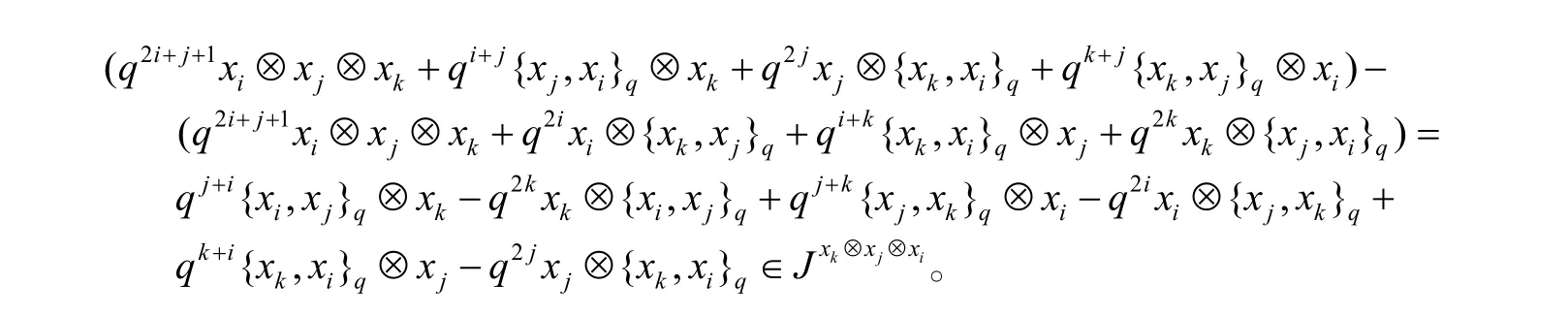
推论σ 从q -李代数qL到普遍包络代数的典范映射σ是单射。

3 结论

本文中我们给出了一般q-李代数的普遍包络代数U(Lq)，对 U(Lq)的相关性质进行了讨论，证明了 U(Lq)对应的q-PBW定理，并给出了它的一组基。至此，对一般q-李代数的研究就较为完善了，在此基础上，我们就可以仿照研究一般意义下量子群的方法，来进一步地研究由一般q-李代数所引入的量子群理论。

[1]KASSEL C.Quantum Groups[M].北京∶世界图书出版公司北京公司,2000∶23-38.

[2]SCHEUNERT M.Generalized Lie algebras[J].J Math Phys.,1979,20(4)∶712-720.

[3]LIU XIAOLEI.Construction of a q-Lie algebra[C]//The Second International Conference on Game Theory and Applications.England,UK∶World Academic Union,2007∶121-122.

[4]JAMES E HUMPHREYS.Introduction to Lie Algebras and Representation Theory[M].New York∶Springer-Verlag,1972∶153-161.

[5]李晓沛,杨必中,徐沈新.一类广义李代数[J].湖南师范大学自然科学学报,2003,26(3)∶23-26.

[6]李晓沛,徐沈新.τ-李代数的普遍包络代数及其PBW定理[J].湖南大学学报,2003,30(6)∶6-9.

[7]陈育明.q-类似virasoro代数的自同构[J].泉州师范大学学报,2008,26(2)∶39-43.

[8]顾兴民,张娟娟,王宪栋.由结合代数构造q-李代数及低维q-李代数的分类[J].青岛大学学报,2009,22(1)∶15-17.

[9]汪明义.Hopf代数、Yang-Baxter 方程与量子群[J].西南交通大学学报,2008,35(4)∶425-429.

[10]孟道骥.复半单李代数引论[M].北京∶北京大学出版社,1999∶120-132.

[11]G YU SHEN.Graded Modules of Graded Lie Algebras of Cartan Type(1)-Mixed Product of Modules[M].Scientia Sinica (Ser.A),1986∶575-580.