一类连续线性切换系统的H∞滤波

宋艳荣，王兴平，姚立强，张术东

（海军航空工程学院基础部，山东 烟台 264001）

在复杂的控制工程中，往往会同时出现连续变量动态系统和离散事件动态系统，这两种系统相互混杂和作用，形成统一的动态系统——混杂系统。随着计算机科学和控制理论结合以及控制系统的智能化发展，混杂系统的概念越来越重要，成为新的研究热点。切换系统是一类重要的混杂系统，可以看作是由一组子系统和一个切换策略组成的。其特点是系统离散动态行为表现为系统在一组连续系统进行切换的切换策略。切换系统在生产过程中是广泛存在的，传统的继电器控制是典型的切换系统问题，最优控制中著名的bang—bang 控制问题也是切换系统的一个特例。在复杂的化工系统、电力系统、交通控制系统中都涉及到切换系统。近些年，对切换系统的研究引起了国内外控制界的关注。

对切换系统的研究包含很多典型的控制问题，如文献[1]利用共同Lyapunov函数方法研究了一类切换线性广义系统的稳定性问题；文献[2]基于线性矩阵不等式，研究了一类不确定线性切换系统的H∞鲁棒控制问题；文献[3]则研究了不确定线性切换系统在任意切换规则下的极点配置和H∞鲁棒控制问题。作为重要的滤波问题，也有文献研究。文献[4]研究了一类不确定时滞离散切换系统在任意切换规则下的H∞滤波问题；文献[5]利用切换Lyapunov函数方法，研究了时滞离散切换系统的H∞滤波器的设计问题。

系统的滤波问题就是研究如何在受干扰的系统输出信号中检测出系统状态的问题，这是控制系统中一个重要的问题[6-7]。目前，用来研究状态估计问题的许多方法中，Kalman滤波方法和H∞滤波方法是比较常用的方法。Kalman滤波方法的特点是要求系统的干扰具有已知的统计特征，相较之下，H∞滤波方法则不要求系统的干扰信号的统计特性，只要求干扰的能量有界，同时，H∞滤波方法还对系统的结构不确定具有较好的鲁棒性。正是由于H∞滤波方法的这两个优点，使得人们对H∞滤波产生了极大的兴趣[8-9]。从文献看，切换系统的H∞滤波问题主要集中在离散切换系统，对于连续切换系统的H∞滤波器问题，较少有人研究。

本文主要研究一类连续线性切换系统的H∞滤波器的设计问题。由于滤波器是建立在系统的输出端的，无法实现对系统的切换规则的要求。因此，滤波器的设计是在切换系统是任意切换这一前提下进行的。本文首先基于共同Lyapunov函数方法，给出了切换系统存在H∞滤波器的充分条件；其次，利用线性矩阵不等式技术，把这个条件变成一组线性矩阵不等式(LMIs)的可行解存在问题，进而根据LMIs的可行解给出了H∞滤波器的一个构造性的设计方法；最后，给出的实例验证了用这一方法设计H∞滤波器的有效性和可行性。

1 问题描述及准备工作

考虑如下切换系统

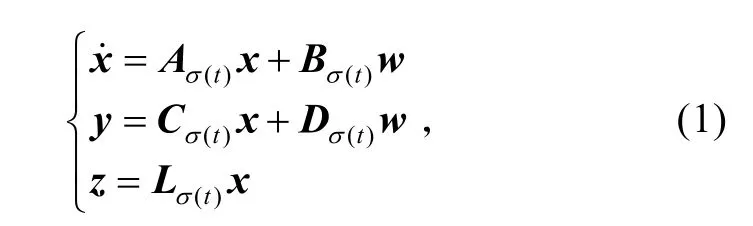
式中：x ∈Rn为系统状态；w ∈Rp且w∈ L2(0,+∞)为能量有限的外部扰动；y ∈Rq为测量输出；z ∈Rm为待估计的信号向量，σ∶[0,+∞) →Λ={1,2,…,N}为切换信号，σ (t)的每一次取值的变化表示一次切换，σ (t)=i ∈Λ表示在t时刻切换系统的第i个子系统在运行；Ai、Bi、Ci、Di、Li(i ∈Λ)为第i个子系统对应的系数矩阵，它们具有相应的维数。

一般系统的H∞滤波问题的提法是：根据系统的测量输出y，给出待估计的信号向量z的估计值zˆ，使得系统在无外部干扰的情况下稳定；在干扰存在，零初始状态条件下，从干扰能量w到估计误差 z−的信号能量的增益小于预先给定的正数γ。对于切换系统(1)，由于系统的状态在不同时刻可能服从不同的动态方程，对系统状态的估计是和各个子系统相关的，所以对系统(1)进行滤波器设计应该对每个子系统都进行滤波器设计，这些滤波器连接在对应子系统的输出端，保证系统在切换时能有效地给出系统的状态估计。

于是对切换系统(1)，本文的目的就是对每一个子系统设计滤波器

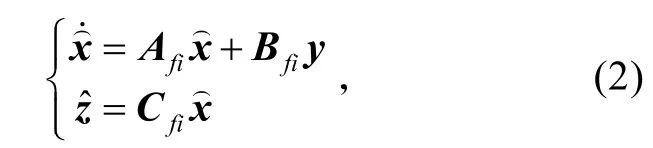
使得式(1)、(2)组成的复合系统在任意切换规则下满足：

1)w=0时，系统渐近稳定；

设计切换系统(1)的滤波器(2)的问题，其实就是确定式(2)中的系数矩阵Afi、Bfi、Cfi、Dfi，使得设计目标中的条件1)、2)成立。

将系统(1)和滤波器(2)组合起来，可得如下滤波误差动态系统

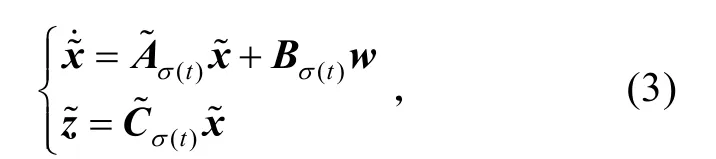
这样，滤波的目的改变为设计恰当的滤波器(2)，即寻求合适的使得滤波误差动态系统(3)满足如下性能：

1)w=0时，系统(3)渐近稳定；

为了方便后面的叙述及证明，引入下面的定义、假设和引理。

定义：如果且则称序列是由切换策略 σ(t) 生成的切换序列。

假设：切换系统的每个子系统总是运行一段时间后才切换到其他的子系统，即每个运行的子系统总有一定的驻留时间。

引理1：[10](Schur 补引理)对于给定的对称阵其中 S11和S22是方阵，以下3个条件是等价的：

1) S＜0；

引理2：[11]设M1和M2是具有适当维数的矩阵，则对任意正数β，均有

2 主要结论

下面给出关于切换系统(1)的H∞滤波器(2)存在的充分条件。

定理1：对于给定的正数γ，如果存在对称正定阵P，使得下列N个矩阵不等式成立

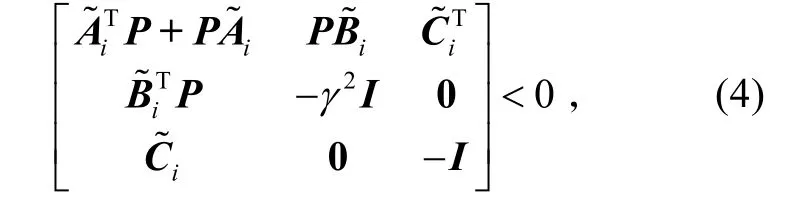
则切换系统(1)存在滤波器(2)，使得滤波误差动态系统(3)满足性能1)和2)。

证明：根据引理1，式(4)可以整理为

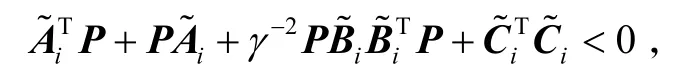
即

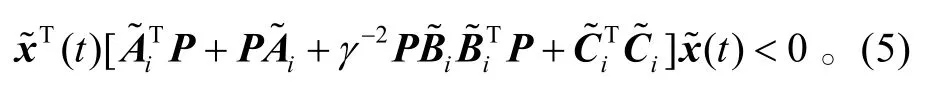
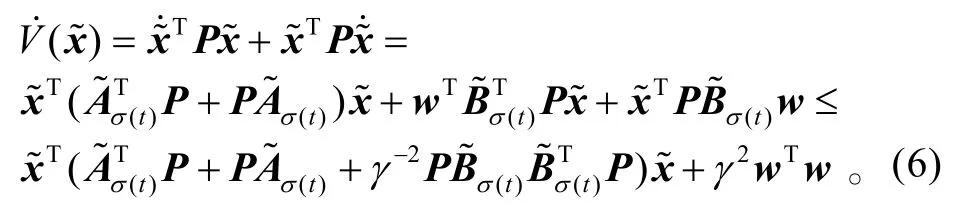
根据切换序列的定义、假设，可知在时间段[tk,tk+1)上，系统(3)的第ik个子系统运行，即系统(3)的切换策略 σ (t)在该时间段上恰好选择第ik个子系统运行。不妨令 ik=i，也就是σ(t)=i,t ∈ [tk,tk+1)。则在时间段 [tk,tk+1)上，当w=0，由式(6)，有

由式(5)可知，在时间段 [tk,tk+1)上，

总结上面的推导，可以看到当w=0时，在时间段 [tk,tk+1)上，由切换策略 σ (t)选择运行的子系统i对应的同理，在其他的时间段上，由切换策略 σ(t)选择运行的子系统也能保证使得成立。因此，当w=0时，在时间段[0,+∞)上，总是成立，即滤波误差动态系统(3)满足性能1)。

下面证明滤波误差动态系统(3)满足性能2)。

在零初始状态条件下，有

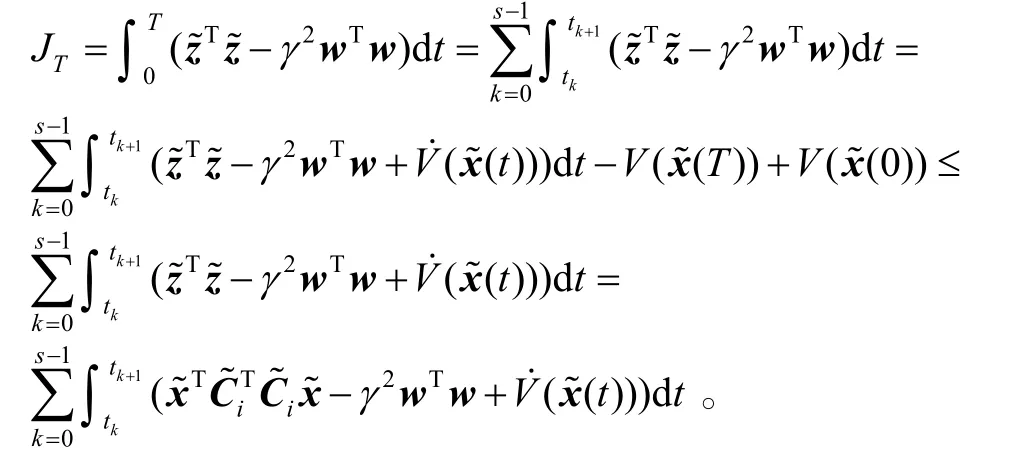
根据式(6)，上式整理为

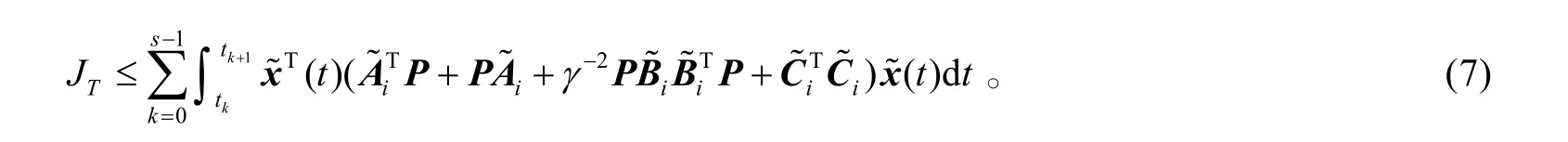
这说明滤波误差动态系统(3)满足性能2)。结论得证。

注：本定理提出的条件是基于切换系统具有共同Lyapunov 这一前提给出的，根据文献[12]中的结论，一个线性切换系统如果在任意切换策略下是一致指数渐进稳定的，则所有切换子系统存在一个齐次的共同Lyapunov函数。这就是说，为了保证滤波器能满足性能指标 1)，假定系统具有一个共同Lyapunov函数是合理的。

定理中的不等式(4)是关于矩阵变量 P、Afi、Bfi、Cfi的一个非线性矩阵不等式，很难求出可行解。为了克服这一困难，我们提出定理2。定理2借助于线性矩阵不等式(LMIs)给出了一个与定理1等价的滤波器存在的充分条件。

定理2：对于给定的正数γ，如果存在对称正定阵X、R和矩阵 Zi、Mi、Ni，使得矩阵不等式(8)和(9)成立，则系统(1)存在H∞滤波器(2)。

式中：i ∈Λ={1,2,…,N}；∗表示对称位置矩阵的转置。

证明：由定理1可知，如果存在对称正定阵P使得(4)成立，则系统(1)存在H∞滤波器(2)，即滤波误差动态系统(3)满足性能1)和2)。

根据P是对称正定阵，有

由于PP−1=I，可得

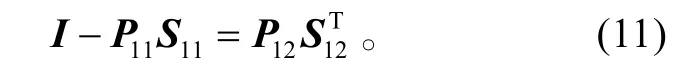
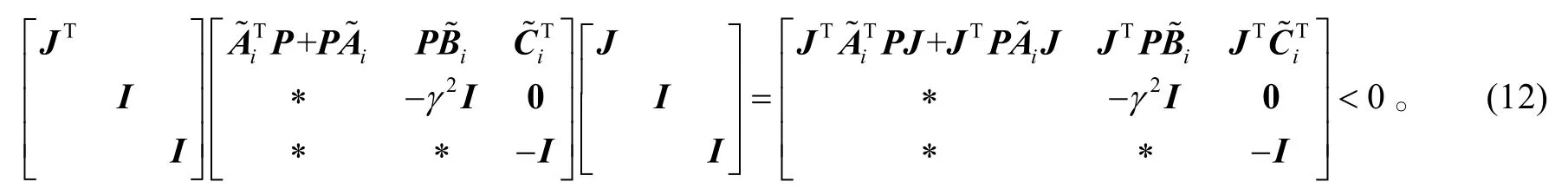
令

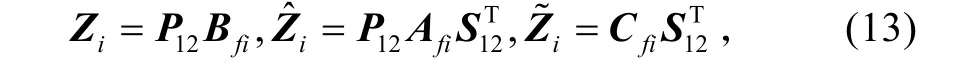
将式(13)代入，得到

令

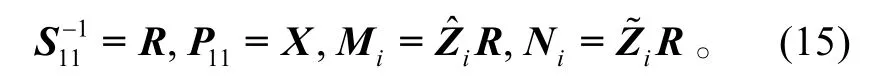
将式(15)代入式(14)，则式(14)整理为式(8)。

另一方面，由于定理1 中的P是正定阵，即P＞0，有

根据式(10)、式(15)和式(16)知道P＞0与式(9)等价。结论得证。

上面的推导表明定理2是与定理1 等价的滤波器存在的充分条件。

进一步，若X、R、Zi、Mi、Ni(i ∈Λ)是线性矩阵不等式(8)和(9)的可行解，根据式(11)和式(15)，利用I−R−1X的奇异值分解得到满秩矩阵 P12、S12，由式(13)和式(15)即可求得H∞滤波器(2)的系数矩阵为

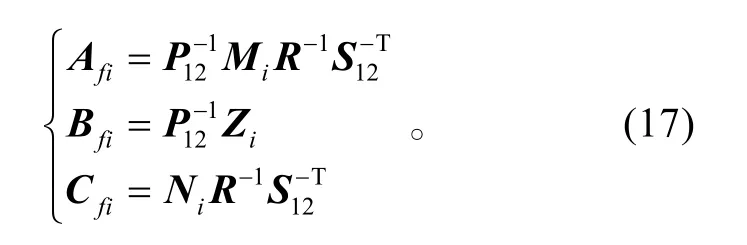
3 仿真实例

考虑如系统(1)的切换系统(N=2)

选取γ=0.2，采用本文方法设计H∞滤波器。

首先，利用Matlab的LMI 工具箱求解线性矩阵不等式(8)和(9)得：

然后，通过满秩分解求得：

最后，利用式(17)得到构造H∞滤波器所需的系数矩阵为：

根据求得的滤波器参数，进一步通过仿真来验证本文定理的正确性。

具体做法是，将上面求得的各种参数代入系统中，选取强度为5的白噪声作为能量有限的干扰w，采样时间为0.1 s，在10 s时间内，任意选取切换策略，这里选取的切换策略是

由该切换策略 σ(t)生成的切换序列是{(0,1),(3,2),(8,1)}，即切换系统在初始时刻进入子系统1 运行，运行3 s后切换到子系统2 运行，子系统2 运行5 s后又切换回到子系统1，运行2 s。

分析得到的待估计信号z和估计信号ˆz的变化曲线，可得如图1所示的切换系统(1)的滤波跟踪图，图中，虚线表示切换系统(1)的待估计信号z的变化曲线，实线表示估计信号ˆz的变化曲线。

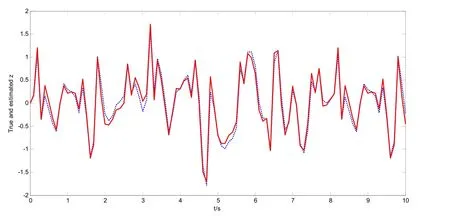
图1 切换系统(1)的滤波跟踪图

通过仿真实例结合得到的仿真图形可以知道，当切换系统(1)在我们随意选取的切换策略下运行时，H∞滤波器(2)可以很好地跟踪估计信号向量。事实上，可以验证对于任意的切换策略，设计的滤波器都能很好地跟踪估计信号向量。因此，本文设计的H∞滤波器符合要求并且性能良好。

4 结束语

本文针对一类连续线性切换系统研究了H∞滤波问题，给出了H∞滤波器存在的充分条件并将该条件转化为一组线性矩阵不等式的可行解问题。同时，借助线性矩阵不等式的可行解，给出了H∞滤波器的设计方法。最后通过仿真实例说明用该方法设计H∞滤波器的可行性。

[1]尹玉娟,刘玉忠,赵军.一类切换线性广义系统的稳定性[J].控制与决策,2006,21(1)∶24-27.

[2]孙文安,赵军.基于LMIs的不确定线性切换系统H∞鲁棒控制[J].控制与决策,2005,20(6)∶650-655.

[3]闻继伟,刘飞.不确定线性切换系统的H∞鲁棒控制和极点配置[J].东南大学学报∶自然科学版,2008,38(增刊 Ⅱ)∶163-167.

[4]LIU X W,DUAN G R.Robust H∞filtering for switched discrete-time systems with time-delays [J].黑龙江大学自然科学学报,2007,24(6)∶736-742.

[5]DU D S,JIANG B,SHI P,ZHOU S S.H∞filtering of discrete-time switched systems with slate delays via switched Lyapunov function approach[J].IEEE Transactions on Automatic Control,2007,52(8)∶1520-1525.

[6]GEROMEL J C,OLIVEIRA M C D.H2 and H∞robust filtering for convex bounded uncertain systems[J].IEEE Transactions on Automatic Control,2001,46(1)∶100-107.

[7]PLIA A W,SHAKED U,SOUZA C E D.H∞filtering for continuous-time linear systems with delay[J].IEEE Transactions on Automatic Control,1999,44(7)∶1412-1417.

[8]XU S Y,JAM J,GAO H J,ZOU Y.Robust H∞filtering for uncertain discrete stochastic systems with time delays[J].Circuits Systems Signal Procession,2005,24(6)∶753-770.

[9]XIE L H,LU L L,ZHANG D,ZHANG H S.Improved robust H2 and H∞filtering for uncertain discrete-time systems[J].Automatic,2004,40(5)∶873-880.

[10]刘永清,唐功有.大型动力系统的理论与应用：滞后、稳定与控制[M].广州∶华南理工大学出版社,1992.

[11]PETERSEN I R.A stabilization algorithm for a class of uncertain linear systems[J].Systems and Control Letters,1987,7(8)∶351-357.

[12]LIBERZON D,MORSE A S.Basic problems in stability and design of switched systems[J].Control Systems Magazine,1999,19(5)∶59-70.