改进的细菌觅食算法在航空装备维修任务调度优化中的应用

崔 嘉，杨 林，胡卫民

（1.海军航空工程学院控制工程系，山东 烟台 264001；2.海军装备部军械保障部，北京 100841）

1 概述

细菌觅食优化(Bacteria Foraging Optimization，BFO)算法是由Passino 于2002年提出的一种仿生随机搜索算法，其生物学基础是大肠杆菌在觅食过程中体现出来的智能行为。大肠杆菌自身有一个控制系统，该系统指导着其在寻找食物过程中的行为，包括趋化、复制和迁徙(又称消除—驱散)等3个步骤[1-2]，并对每一次状态的改变进行效果评价，进而为下一步活动提供信息。在这个系统的控制下，大肠杆菌将逐渐朝食物源的方向靠近。在BFO模型中，搜索过程通过营养分布函数来判断搜索算法的优劣，优化问题的解对应搜索空间中的细菌的状态，即优化函数的适应度值。航空装备修理定检工作涉及多个车间、工种和工序，利用优化算法对定检修理工作进行有效的组织、精确高效调度，可实现各类保障资源的优化组合与合理分配，降低保障维修费用。通过对BFO算法进行改进，并在航空装备定检维修任务调度拟实优化系统中进行了应用。

2 对原始BFO算法改进

2.1 细菌觅食行为中的群体改进

原始BFO算法搜索解空间时，采用的是个体间感应机制，细菌每移动到新的位置，将根据式(1)计算个体间感应值(或称cell-to-cell 感应值)[3]：

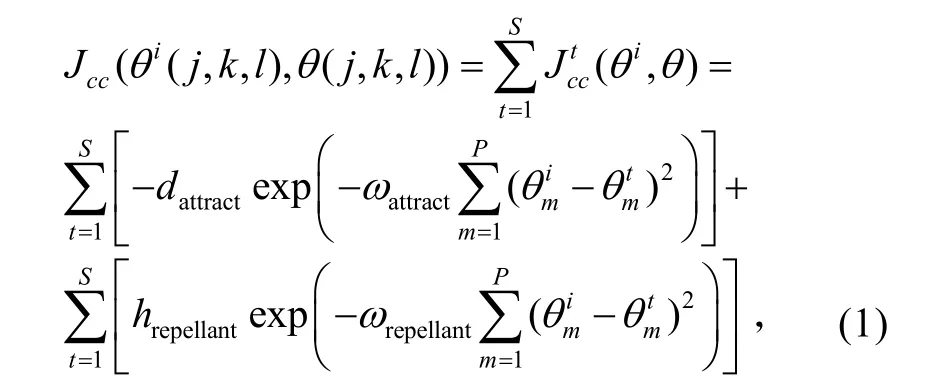
式中：Jcc(θi(j,k,l),θ (j,k,l))表示在第j次趋向操作、第k次复制、第l次迁徙操作时，第i个细菌的个体间感应值之和；Jct c(θi,θ)表示第t个细菌和第i个细菌之间的群体感应值；dattract和ωattract分别表示吸引因子的数量和释放速率；hrepellant和ωrepellant分别表示排斥因子的数量和释放速率；S表示细菌种群规模；p表示细菌搜索环境的维数；θmi表示第i个细菌所在位置的第m 维。

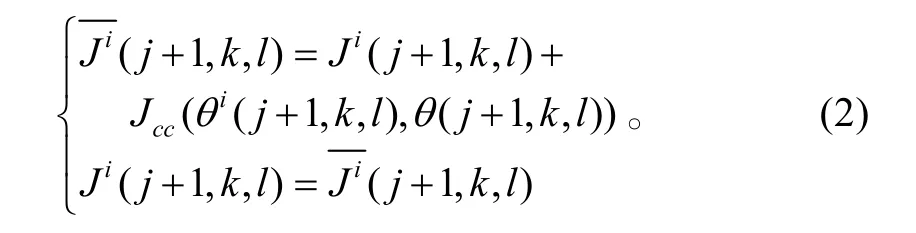
根据式(2)将感应值叠加到细菌的适应值上，这种基于个体间的感应机制，有助于保持种群的多样性，也增加了细菌群体跳出局部最优的可能性。但也有可能使得接近最优的细菌遭到驱散，导致优化进程延缓。很多细菌聚集到全局最优位置附近，但因为数量的增多导致该区域产生的排斥因子浓度升高，反而可能会将位置最好的细菌驱逐出最优区域，造成精度下降。

借鉴粒子群优化(Partical Swarm Optimization，PSO)算法[4-6]中粒子自我总结并向最优粒子学习，向群体内历史最优点靠拢的群体感应机制，对BFO算法进行改进。在每次趋向操作完成后，进行类PSO的个体—群体感应操作(或称 cell-to-swarm 感应值)：细菌个体感知周围环境，试探搜索菌群中是否存在位置最好的细菌。如有，记忆其位置；否则，记忆自身当前位置。下一次趋向操作时，细菌每移动到新的位置，就根据式(3)向记忆位置靠拢。

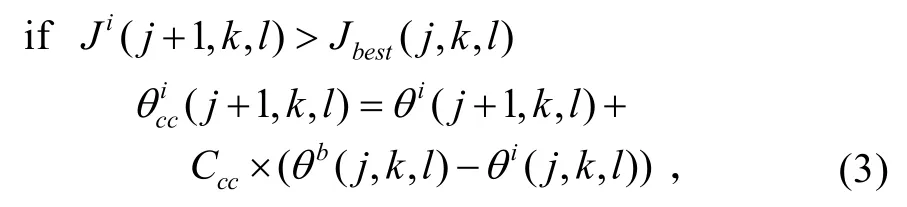
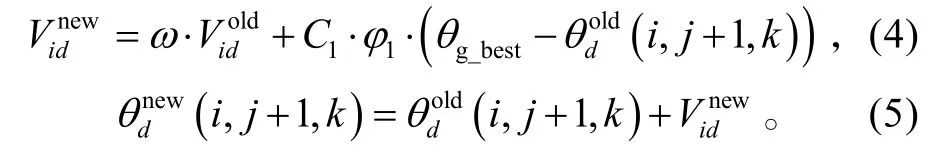
式(4)、(5)中：ω为惯性权重，使细菌保持运动惯性和扩展搜索空间的趋势，有能力探索新区域；1C为学习因子，或称加速度常数；ϕ1是[0,1]区间内均匀分布的伪随机数；Vi为个体细菌i的速度。

经过改进后，新的群体感应机制允许细菌个体利用同伴的经验来指导自己的游动路线，这种信念吸引机制加快了在解空间中的全局搜索速度，同时也有助于细菌个体跳出局部最优，以及避免了细菌从全局最优区域逃逸的可能。

2.2 细菌趋向操作的可变步长改进

原始BFO算法中，细菌前移的计算方法如式(6)[8]：

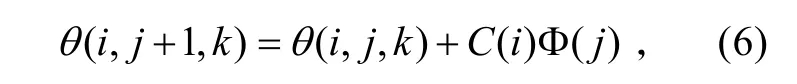
细菌在生命周期中，可能产生基因突变，优良的细菌可以具备较强的行动能力，其迁徙时进行的趋向行为可以幅度更大，这样更有利于提高细菌的觅食速度。为了进一步加快搜索速度，提高优化前期的全局搜索能力和优化后期的局部搜索能力，可对BFO算法进行进一步改进，将趋向操作时的步长设置为动态调整值，而非固定值[7]，如式(7)：

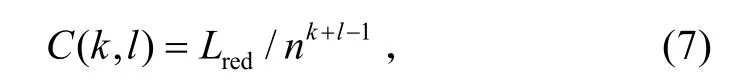
式中：C (k,l)表示细菌第k次复制、第l次迁徙时的趋向操作步长；Lred表示初始趋向步长；n表示控制步长下降梯度的参数。

在优化前期，即k+l较小时，C (k,l) 增大，提高了个体解空间移动能力，避免在局部范围过多地消耗搜索时间。在优化后期，k+l 逐渐增大，C (k,l)减小，使得个体在接近全局最优点附近时的局部搜索能力增强，保证算法最终趋近全局最优点。映射到细菌觅食行为中，相当于加快了细菌的觅食能力和速度，从细菌群体角度看，是保留了优秀细菌的基因，增强了细菌群的迁徙能力。

2.3 改进的快速细菌群游优化算法设计

改进后的算法流程图如图1。

2.4 非线性模型的优化问题分析

2.4.1 典型非线性模型

选取Shaffer函数作为典型非线性模型进行仿真，其描述为：

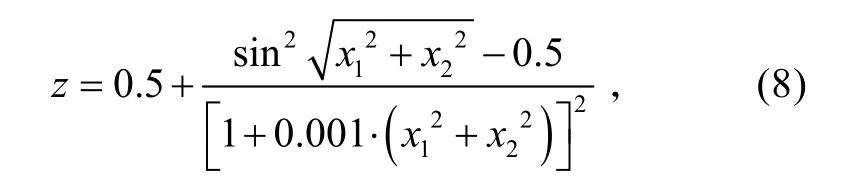
式中：x1,x2∈[−2,2]。选取z 作为适应度函数，种群规模S=40，趋向次数Nc=100，最大前趋步数Ns=4，复制代数Nre=4，迁徙次数Ned=2，迁徙概率 Ped=0.25。仿真结果如图2～4所示：

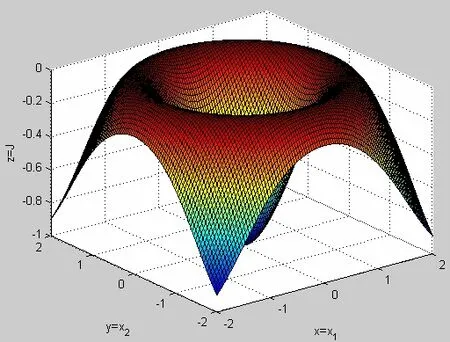
图2 能量浓度地形图(山谷=食物，山峰=有害物质)

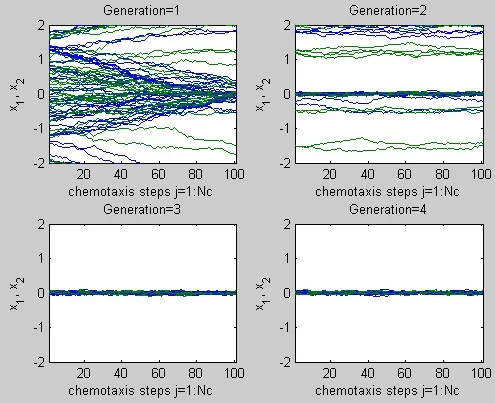
图3 细菌迁徙数为1时1～4代的运动轨迹

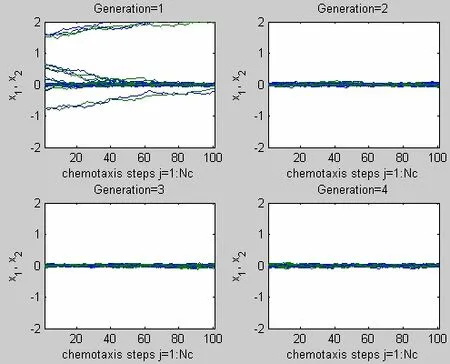
图4 细菌迁徙数为2时1～4代的运动轨迹

2.4.2 仿真结果分析

由仿真结果可知，第1代细菌随机散布在待优化区域，进行趋向行为和群体聚集行为，细菌经过筛选后繁殖进入第2代，并重复第1代的行为不断朝向食物聚集，到第4代时，细菌已在小范围区域聚集。迁徙数为2时，细菌在前4代的基础上，先按迁徙概率执行迁徙操作，再继续搜索行为，到第2代时已基本聚集到最优区域，后2代时这一区域不断收敛，直至第4代已收敛到很小的区域，由此可见该算法的有效性。在迁徙数为2时，细菌已很好地收敛到最优区域，可知该算法简单且收敛速度快。

1)迭代次数测试。

以精度为0.000 01时所需要的迭代次数作为比较，结果如表1所示。

表1 迭代次数结果比较

2)收敛性测试。

设置最大迭代次数为100，每种算法运行100次，计算平均最优解，结果如表2所示。

表2 平均最优解比较

由以上数据分析可知，菌群优化算法用于该模型的优化问题的求解十分有效，对其进行的改进可明显增强寻优能力，有效避免陷入局部最优。

3 BFO算法在任务调度优化中的应用

3.1 任务调度问题描述

一般地，对于有n个工件(对应我航空兵修理厂则为飞机上的待修部件等)，m个机器(对应我航空兵修理厂则为车间里的维修保障装设备)的车间，在可行调度中确定每个工序的开始时间 sij和工序加工时间 tij，使总完工时间 fmax最小，即构成了维修作业调度问题。即：

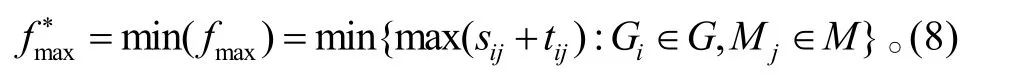
如果存在一个确定的工件排列阵MJ∗，使得整个维修任务时间函数满足式(8)，且与机器顺序阵MG相容，则称MJ∗为车间作业调度问题在此目标函数下的最优解[9]。

在装备维修保障系统中，作战部队、阵地及装备都有相对确定的维修保养机构(如维修分队(所)，它们的位置相对固定)，一个维修分队可以保障若干部队装备的维修。进行飞机定检维修的场所一般情况下是在维修小组所在的地点，通常为修理厂机棚或停机坪。因此，保障资源与故障装备、维修小组的距离问题可以不予考虑。

利用式(9)描述的细菌觅食算法算子来表示某工件在某种机器加工的排列下加工所用的时间[10]：

式中：J (i,j,k,l)=J (i,j,k,l)+Jcc(θi(j,k,l))表示一个关于细菌觅食算子的工件排序序列，采用细菌觅食算法对该排列进行搜索，然后求得MJ∗，这就是基于群体的细菌觅食算法在车间调度系统中的应用。

使用改进后的细菌觅食优化算法求解该类调度优化问题的一般过程应为：①对问题进行编码；②执行解码策略；③设计评价函数，产生初始解群体；④利用群体感应机制，进行全局寻优。

3.2 问题的编码

采用基于操作的编码策略，将每个可行解用n×m个代表操作的编号组成，构成符合工艺约束条件的所有操作的一个排列，编码序列中的数字表示待修部件的编号。待修部件i的第j次出现，表示待修部件i的第j个操作或第j 道工序(i=1,2,⋅⋅⋅,n;j=1,2,⋅⋅⋅,m)。由于在编码时就考虑到了工艺约束，因此在对编码进行置换变换时，可以得到可行解。表3给出了典型的3×3调度问题的工艺约束，图5给出了一个编码示例[11]。

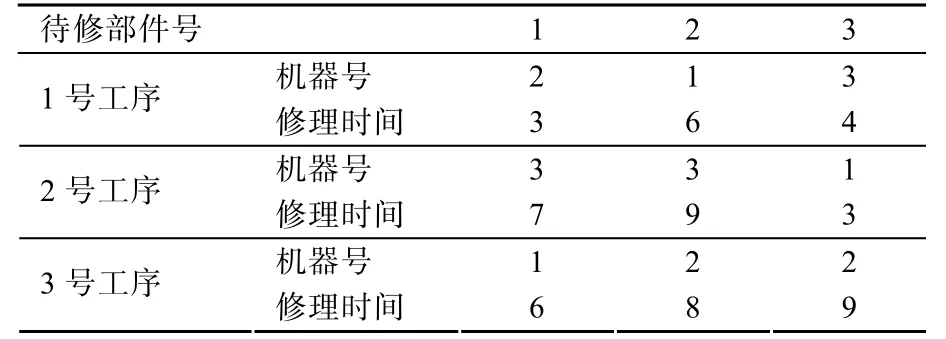
表3 3×3 车间调度问题工艺约束

在表3给出的工艺约束下，设一个可行解[3 1 1 2 1 3 2 2 3]，图5所示编码对应的工序序列为图6。

3.3 解码策略

对于生成的可行解，如果要应用于调度问题实际，则需要将其转换成对应的可行活动调度，这个过程称为解码。一个可行解可以解码出多种调度，即一个操作序列对应多个调度方案，通过对解码过程进行优化，则可以从操作序列中得到更优的调度方案[12]。

优化方法：判断当前操作是否可插入已存在的空闲段中，如果可进行插入，则会在很大程度上缩小可行调度所消耗的时间，从而求得最优或准最优调度方案。

3.4 BFO个体搜索策略应用

细菌个体在觅食过程中，依据自身的信息来决定其搜索方向的操作(基于个体的搜索策略)具体步骤为：

1)确定细菌群体中将要进行自身搜索的个体细菌I。

2)在当前个体代表的可行解的编码序列上随机选定两个位置，称这两个位置之间的编码序列区间为稳定区。稳定区中的各个操作顺序(即编码)在本次搜索过程中保持不变，相当于此次搜索时随机选定的方向不变。

3)该个体所标识的调度序列被分为3段，除中间的稳定区外，其两侧的操作序列区间被称为置换区间A和置换区间B。在这两个置换区间上分别进行序列重新随机排列，即分别对区间A和区间B 进行置换操作。经过置换后，相当于个体细菌按照事先选定的方向前进了一步。由于采用了基于操作的编码方式，因此随机置换操作后得到的编码序列依然是可行解。

4)对个体细菌的当前位置进行适应度评价。如果新位置更优，则认为这一次的前进改变是正确的，用新位置上的个体替换掉原个体，相当于原个体进行了一次位移。反之，个体回到原来位置，即取消本次的前进操作。

5)当前个体细菌停顿。此时其面临两种选择，一是重新选定一个随机方向，在此进行基于个体的搜索，二是个体马上停止搜索，调度系统跳至下一个进行搜索操作的个体细菌，本轮算法结束。

3.5 改进的群体感应搜索策略

基于群体感应机制所进行的改进搜索策略，具体步骤为：

1)确定细菌群体中目前位置最优的个体 Ic_best，存储其位置和适应度值。

2)确定细菌群体中将要进行搜索的个体细菌I。

3)在最优个体 Ic_best的序列中，随机选定一个编号 Jrand(即工件号)。将来产生的新个体需要保证该编号的开始加工顺序与在最优个体上的位置相同。

4)遍历最优个体 Ic_best，确定该编号 Jrand在最优个体中的位置J

P。5)开始对个体细菌I 进行调整。遍历当前个体I，找到序列中编号 Jrand的起始位置(即第Jrand号工件在当前序列中进行第1 道加工工序时的位置)，将其与位置J

P的编号进行置换。6)对个体细菌的当前位置进行基于个体的评价。

7)对个体细菌的当前位置进行基于群体的评价。与细菌群体中目前位置最优的个体 Ic_best相比，如果当前个体I的新位置更优，则认为这一次的前进改变是使得当前个体移动到了群体最优的位置，于是最优个体细菌更新为当前个体细菌的位置，群最优适应度值也相应进行更新。反之，不做任何操作。

8)当前个体细菌停顿。此时其面临两种选择，一是重新选定一个随机方向，在此进行基于个体的搜索，二是个体马上停止搜索，调度系统跳至下一个进行搜索操作的个体细菌，本轮算法结束。

4 算法实现

图7为使用改进的细菌觅食算法作为任务优化调度算法库的处理流程。

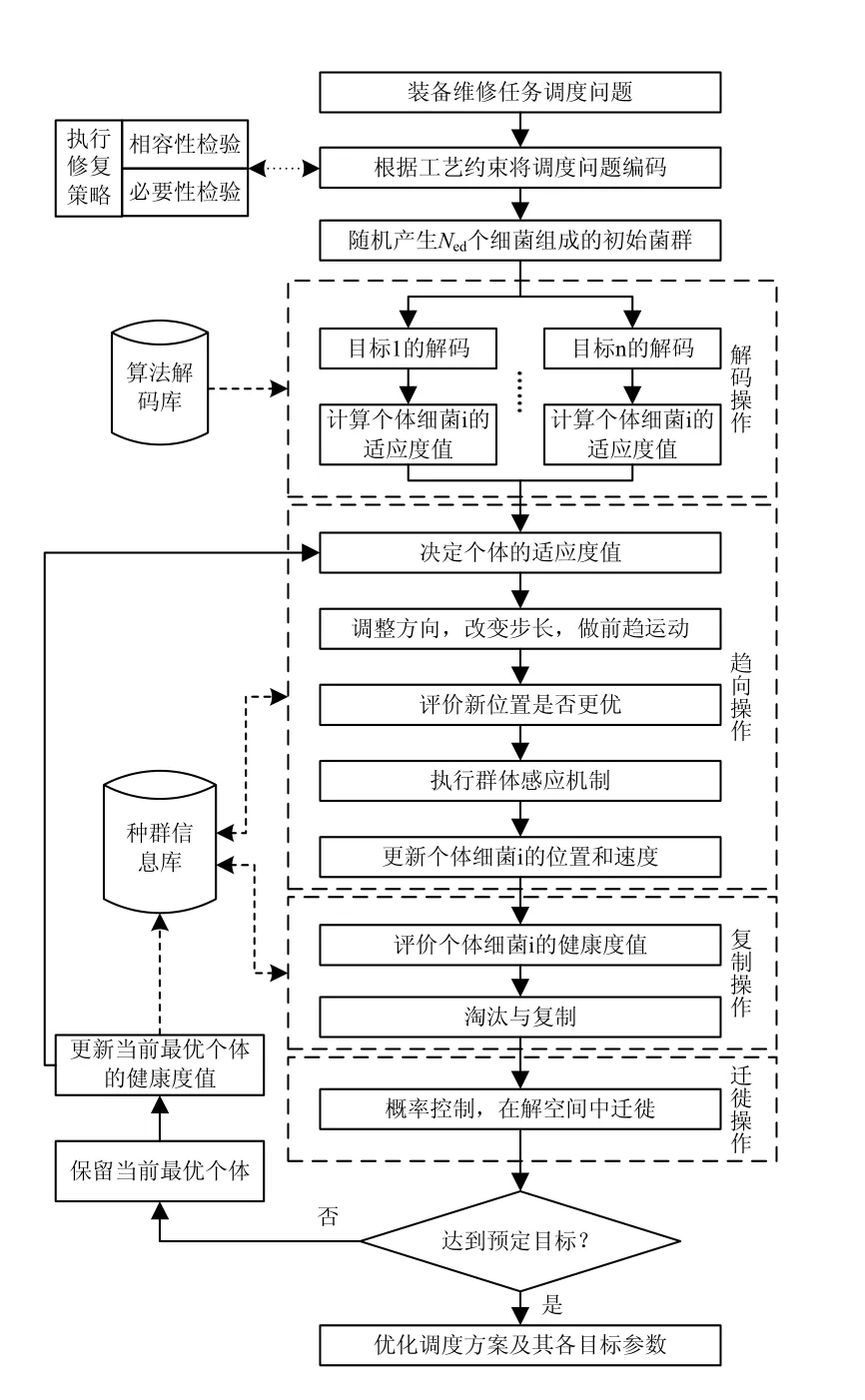
图7 任务优化调度算法库的处理流程

利用该算法库，对实际问题进行验证。工序信息如表4所示。

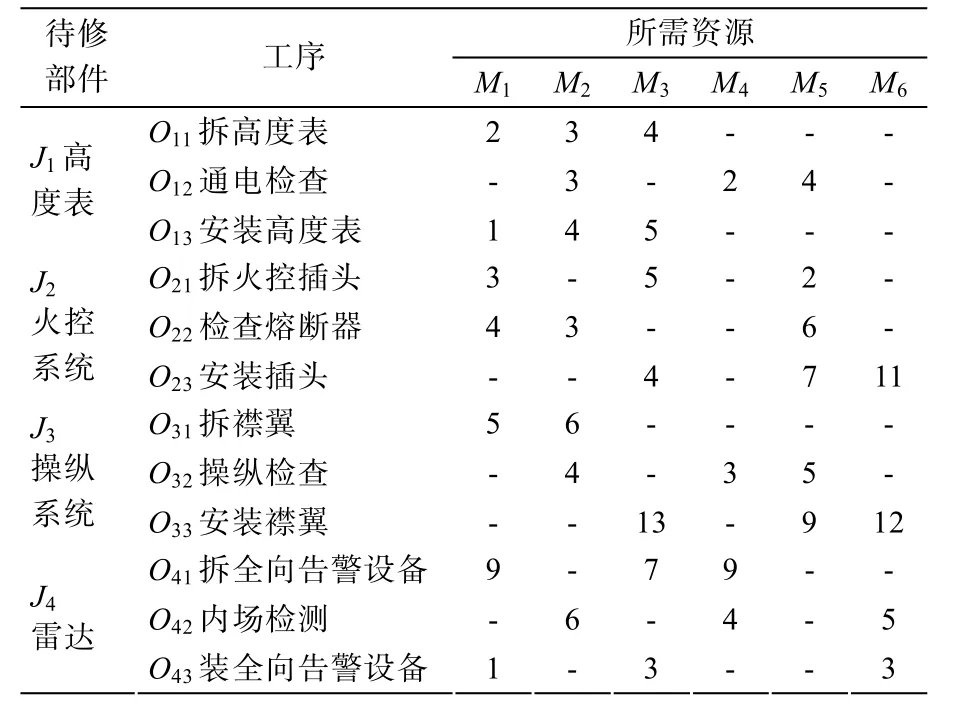
表4 某型飞机400 h 定检工作部分工序

对算法进行了50次运算，均收敛在f (Tj∗)=17，寻优结束后，得到的最优工序序列为

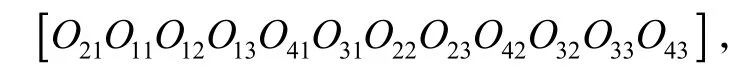
作业路线如表5所示，图8为对应的甘特图。

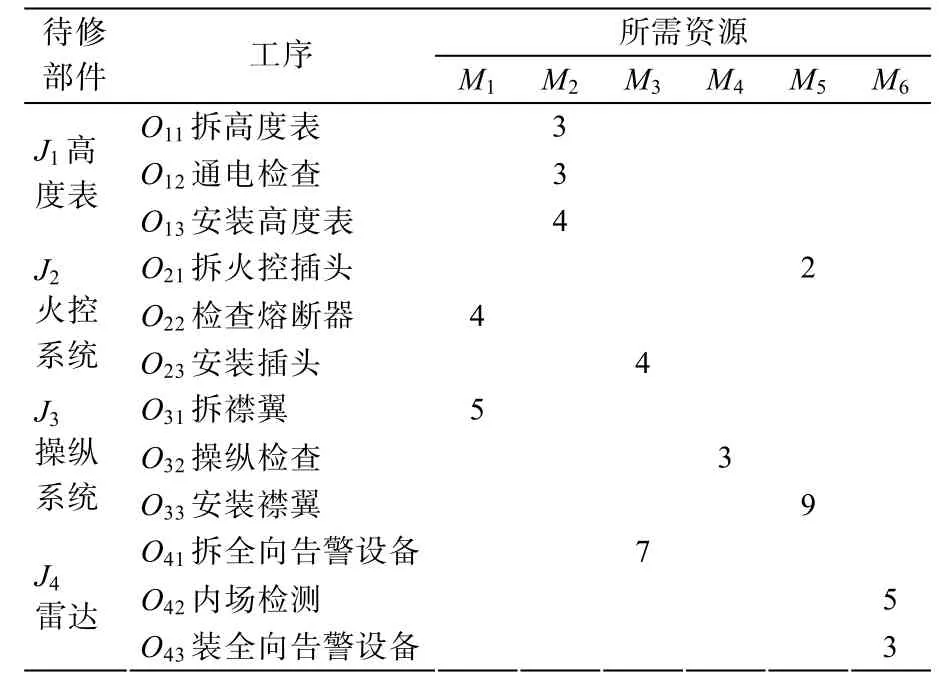
表5 作业路线

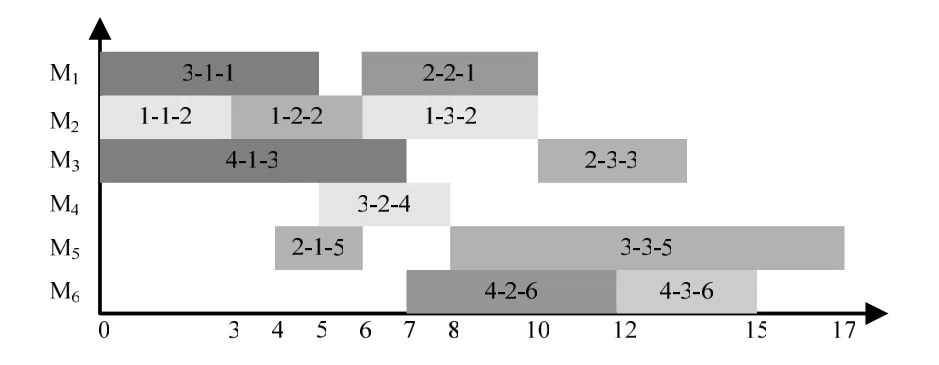
图8 调度结果甘特图

5 结束语

对细菌觅食优化算法进行了改进，并将其应用于航空装备定检修理的任务优化调度系统中，该系统可建立较为完整的飞机定检维修任务模型，能够有效求解维修任务的动态调度问题，并实现对维修保障资源的优化组合与合理分配。

[1]MISHRA S.A hybrid least square-fuzzy bacteria foraging strategy for harmonic estimation[J].IEEE Trans.on Evolutionary Computation,2005,9(1)∶61-73.

[2]PASSINO K M.Biomimicry of bacterial foraging for distributed optimization and control[R].IEEE Control System Magazine,2002,22(3)∶52-67.

[3]DATTA T,MISRA I S.Improved adaptive bacteria foraging algorithm in optimization of antenna array for faster convergence[J].Progress in Electromagnetic Research C,2008,1(1)∶143-157.

[4]KENNEDY J,EBERHART R C.Particle swarm optimization[C]//Proceedings of IEEE International Conference on Neural Networks.NewYork,1995∶1942-1948.

[5]EBERHART R C,KENNEDY J.A new optimizer using particle swarm theory[C]//Proceedings of the 6th international symposium on micro machine and human science.Nagoya,Japan,1995∶39-43.

[6]SHI Y H,EBERHART R C.A modified particle swarm optimizer[C]//IEEE International Conference on Evolutionary Computation.Anchorage,Alaska,USA,1998∶69-73.

[7]储颖,糜华,纪震,等.基于粒子群优化的快速细菌群游算法[J].数据采集与处理,2010,25(4)∶442-448.

[8]DAS S,BISWAS A,DASGUPTA S,et al.Bacterial foraging optimization algorithm∶theoretical foundations,analysis,and applications[J].Foundations of Comput Inte.,2009,3∶23-55.

[9]王书锋,邹益仁.车间作业调度技术问题简明综述[J].系统工程理论与实践,2003,23(1)∶49-50.

[10]王文耀,涂海宁,夏芳臣,等.基于细菌觅食算法车间调度系统的研究[J].现代制造技术与装备,2009(2)∶7-8.

[11]梁艳春.群智能优化算法理论与应用[M].北京∶科学出版社,2009∶157-162.

[12]张娜.细菌觅食优化算法求解车间调度问题的研究[D].长春∶吉林大学,2007.