近尾迹中平板对钝物体的干扰
于宪钊,苏玉民,王兆立
(哈尔滨工程大学 水下机器人技术国防科技重点实验室,黑龙江 哈尔滨 150001)
钝物体在海洋钻井平台、海底管道、各种流体机械等工程领域中都有广泛的应用.钝物体尾流中出现的周期性旋涡脱落,可以诱发作用在物体上周期性交变力,又会激起结构振动,因此涡致振动是具有重要实际意义的研究课题.
圆柱和方柱是钝物体的2类典型形式,对其流体动力性能的实验和数值计算的研究很多[1-2].Okajima等[3-4]分析了方柱截面边长比对其流体动力性能以及噪声特性的影响;A.K.Saha等[5]对低Re数的三维方柱的流场特性做了数值计算;Ahmad Sohankar等[6]采用直接数值模拟方法计算了二维、三维方柱的绕流流场;Ian Taylor等[7-8]研究了不同边长比的方柱在不同入射角时的流体动力性能.
很多学者通过在钝物体上游或下游布置干扰体控制尾涡脱落的方法减小作用在钝物体上周期性交变力,进而实现结构减振、降噪的目的[9-10].Md.Mahbub Alam等[11-13]研究了前后布置的柱体的流场结构;Donghyun You等[14]研究了圆柱下游布置分割板对流场的影响,研究表明圆柱的升力、阻力、斯特罗哈数随分隔板长度的改变变化明显.L.Zhou等[15]通过在方柱上游垂直布置一平板来控制方柱的受力.最新的研究是Con J.Doolan[16]采用Open FOAM方法数值分析了方柱近尾迹中水平布置的平板对方柱流体动力性能的影响.
本文采用有限体积法求解Navier-Stokes方程,计算了不同截面形状的钝物体(方柱、圆柱)近尾迹中水平布置的平板对上游钝物体流体动力性能的影响,探讨了Re数、平板布置位置以及平板尺度对上游钝物体的干扰效果.
1 数值计算的基本方法
本文采用有限体积法(finite volume method,FVM)求解二维粘性不可压缩Navier-Stokes方程,分别计算了Re为150和2.19×105时不同截面形状钝物体的流体动力性能.对于Re=150的情形,采用层流模型直接求解即可,但对于Re=2.19×105的湍流流场,则需引入湍流模型以封闭Navier-Stokes方程,本文采用工程上应用较多的标准k-ε模型并结合标准壁面函数进行求解.
无因次的阻力系数、升力系数按下式定义:

式中Fd、Fl分别为作用在物体上的升力和阻力,ρ为介质密度,U为自由来流速度,D为特征长度.
2 数值计算结果分析
2.1 平板对方柱流场的干扰
首先计算了静止平板对方柱流场的干扰,为了与文献[17]对比,取自由来流的速度入口位于方柱上游10D处,压力出口位于方柱下游20D处,周向零剪力壁面位于距方柱20D处.取平板特征长度C= 0.834D,置于方柱下游L=2.37D处,Re=150(D= 0.001 m,U=2.19 m/s).采用结构化网格离散计算区域,方柱壁面处第一层网格高度Δc=0.016 7D,网格数量60 400,计算网格及坐标系统如图1所示.
计算了Re=150时单独方柱的流场参数,并同其他数值计算结果以及实验结果相对比如表1所示,可以看出本文采用FVM方法的计算结果同实验以及其他数值方法的计算结果吻合良好,验证了FVM方法的有效性和准确性.

图1 计算网格及坐标系统Fig.1 Computation grid and coordinate system

表1 Re=150单独方柱流场参数计算结果比较Tab le 1 Com parison of flow parameters of single square cylinder w ith experimental and other numerical results at Re=150
在方柱近尾迹区域布置平板后,方柱的流体动力性能如表2所示,可见采用FVM方法的计算结果与文献[16]的结果吻合良好,布置平板后方柱的尾涡脱落频率下降(St下降),方柱上的平均升力系数下降为单独方柱的21%,平均阻力系数也略有减小,由此导致的振动和噪声也会得到相应的控制.

表2 Re=150平板对方柱流场参数的影响Table 2 Com parison of flow parameters of square cylinder for the single cylinder and cylinder-p late system w ith other numerical results at Re=150
布置平板前后方柱的阻力系数、升力系数收敛曲线如图2所示,横轴为无因次的时间参量.可见布置平板后方柱升力系数、阻力系数下降明显,同时升力系数波动周期约为阻力系数波动周期2倍.

图2 布置平板前后方柱的升力、阻力系数曲线Fig.2 Drag and lift coefficient curve of square cylinder w ith and w ithout p late
方柱尾流场中涡量的分布如图3所示,可见在方柱近尾迹区域布置的平板干扰了方柱原本的尾流场,抑制了方柱尾涡的脱落,平板前后缘有明显的一对旋涡生成,方柱与平板之间不再形成大尺度的涡,同时可以观测到增加平板干扰后尾涡脱落周期明显增大.

图3 布置平板对方柱尾涡脱落的影响Fig.3 Interaction of plate to square cylinder vortex shedding
2.2 平板对圆柱流场的干扰
在海洋工程领域,圆柱较方柱有着更广泛的应用,大量的水下载体中都存在着圆形或近似于圆形的截面,因此本文计算了一个Re=100(D=0.01 m,U=0.146 m/s)的圆柱以及在其近尾迹区域水平布置的平板对它的干扰作用.
对于圆柱的流体动力性能,从前的学者已经做了大量、全面的工作,既有数值计算,也有实验研究可以相互对比验证,文献[17]计算的Re=100时圆柱的阻力系数通过实验拟合得到了一个关于圆柱斯特罗哈数的普适关系:
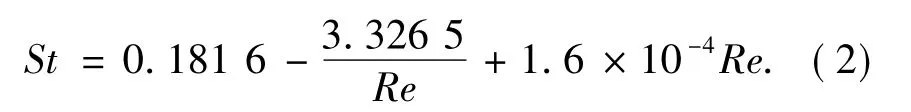
由式(2)可得Re=100时St=0.164.布置平板前后圆柱的升力系数曲线如图4所示,可见布置平板后圆柱升力系数下降明显.

图4 圆柱的升力系数曲线Fig.4 Lift coefficient curve of circular cylinder w ith and w ithout plate

表3 Re=100平板对圆柱的流场参数影响Table 3 Comparison of flow parameters of circular cylinder for the single cylinder and cylinder-plate system w ith other results at Re=100
2.3 平板对高Re数方柱流场的干扰
对于海洋工程领域的钝物体绕流问题,高Re数下的流场计算更具有实际应用意义,由于需要充分考虑粘性的影响,因此层流模型不适用于高Re数下的流场计算,本文采用标准湍流模型计算Re=2.19× 105时布置平板前后上游方柱的流体动力性能.

表4 Re=2.19×105平板对方柱流场参数的影响Table 4 Comparison of flow parameters of square cylinder for the single cylinder and cylinder-p late system at Re=2.19×105

图5 Re=2.19×105平板对方柱升力系数的影响Fig.5 Influence of p late to lift coefficient of square cylinder at Re=2.19×105
2.4 平板布置位置的影响
平板布置位置的不同,对上游钝物体的干扰效果也不同,本文依次计算了Re=150时,平板置于方柱下游L=1.37D,1.87D,2.37D,2.87D,2.97D,3.07D,3.17D,3.27D,3.37D处时,上游方柱的流体动力性能,如图6所示.
计算表明只有平板布置在合适的区间内,才会有效达到降低方柱的斯特罗哈数以及作用在方柱上的周期性交变力的目的,较为合适的平板布置位置应当在L在1.87D~3.17D之间,平板与方柱间距离太近、太远都不会达到很好的减振效果,距离太近则对方柱的影响较小,布置太远则会适得其反,尤其是L=3.27D,3.37D时,方柱的升力系数明显升高,且高于单独方柱不受平板干扰的情形.

图6 不同平板位置对应的方柱流场参数Fig.6 Flow parameters of square cylinder w ith different plate stations
2.5 平板尺度的影响
不同的平板尺度对方柱流场的影响也不相同,本文数值计算了不同平板长度(C=0.3D,0.5D,0.834D,D,1.5D,1.8D,2D)时方柱的流体动力性能.如图7所示,可以看出随着平板长度的增加,上游方柱的都随之下降,且下降趋势随平板尺度的增加而趋于平缓.

图7 不同平板尺度对应的方柱流场参数Fig.7 Flow parameters of square cylinder w ith different plate lengths

图8 不同平板尺度对应的平板流场参数Fig.8 Flow parameters of plate with different plate lengths
3 结论
本文采用有限体积法分析了不同Re数、不同截面形状的钝物体(圆柱、方柱)近尾迹中的平板对上游钝物体流体动力性能的影响.
1)通过和其他学者的研究相对比,验证了在钝物体近尾迹中水平布置的平板可以有效的降低钝物体尾涡脱落频率和作用在钝物体上的周期性交变力.
2)分析了不同的平板布置位置对方柱流体动力性能的干扰效果,计算表明存在一个平板布置的最优区间L=0.187D~3.17D,可以有效的降低作用在方柱上的周期性交变力和St,过近的平板布置位置干扰效果不明显,过远的布置位置则会增大作用在方柱上的周期性交变力.
3)分析了不同的平板尺度对方柱流体动力性能的干扰效果.作用在方柱上的周期性交变力随平板尺度的增加而减小,平板的升力系数、阻力系数也随之减小.
[1]CAO S,OZONO S,HIRANO K,TAMURA Y.Vortex shedding and aerodynamic forces on a circular cylinder in linear shear flow at sub critical Reynolds number[J].Journal of Fluids and Structures,2007,23(5):703-714.
[2]OZGOREN M.Flow structure in the downstream of square and circular cylinders[J].Flow Measurement and Instrumentation,2006,17(4):225-235.
[3]ROKIGOU A,KIWATA T,OKAJIMA A.Numerical analysis of aerodynamic sound radiated from rectangular cylinder[J].Journal of Wind Engineering and Industrial Aerodynamics,2008,96(10-11):2203-2216.
[4]OKAJIAMA A.Strouhal numbers of rectangular cylinders[J].Journal of Fluid Mechanics,1982,123:379.
[5]SAHA A K,BISWAS G,MURALIDHAR K.Three-dimensional study of flow past a square cylinder at low Reynolds numbers[J].International Journal of Heat and Fluid Flow,2003,24:54-66.
[6]SOHANKAR A,NORBERG C,DAVIDSON L.Simulation of three-dimensional flow around a square cylinder at moderate Reynolds numbers[J].Physics of Fluids,1999,11 (2):288-306.
[7]TAYLOR I,VEZZA M.Prediction of unsteady flow around square and rectangular section cylinders using a discrete vortex method[J].Journal of Wind Engineering and Industrial Aerodynamics,1999,82(1-3):247-269.
[8]NORBERG C.Flow around rectangular cylinders:pressure forces and wake frequencies[J].Journal of Wind Engineering and Industrial Aerodynamics,1993,49(1/2/3):187-196.
[9]LIOW Y S K,TAN B T,THOMPSON M C,HOURIGAN K.Sound generated in laminar flow past a two-dimensional rectangular cylinder[J].Journal of Sound and Vibration,2006,295(1-2):407-427.
[10]SHAO C P,WEI Q D.Control of vortex shedding from a square cylinder[J].AIAA Journal,2008,46(2):397-407.
[11]ALAM M M,ZHOU Y.Strouhal numbers,forces and flow structures around two tandem cylinders of different diameters[J].Journal of Fluids and Structures,2008,24 (4):505-526.
[12]ALAM M M,ZHOU Y.Phase lag between vortex shedding from two tandem bluff bodies[J].Journal of Fluids and Structures,2007,23(2):339-347.
[13]INOUE O,MORI M,HATAKEYAMA N.Aeolian tones radiated from flow past two square cylinders in tandem[J].Physics of Fluids,2006,18(4):046101-046101-15.
[14]YOU D,CHOI H,CHOI M,KANG S.Control of flow-induced noise behind a circular cylinder using splitter plates[J].AIAA Journal,1998,36(11):1961-1967.
[15]ZHOU L,CHENG M,HUNG K C.Suppression of fluid force on a square cylinder by flow control[J].Journal of Fluids and Structures,2005,21(2):151-167.
[16]DOOLAN C J.Flat-plate interaction with the near wake of a square cylinder[J].AIAA Journal,2009,47(2):475-478.
[17]PARK J,KWON K,CHOI H.Numerical solutions of flow past a circular cylinder at Reynolds numbers up to 160[J].KSME International Journal,1998,12(6):1200-1205.
[18]WILLIAMSON C H K.Defining a universal and continuous Strouhal-Reynolds number relationship for the laminar vortex shedding of a circular cylinder[J].Physics of Fluids,1988,31:2742-2744.

