带有移动摆载荷柔性梁的动力学分析

吴艳红，韩广才

(1.哈尔滨工程大学 机电工程学院，黑龙江 哈尔滨 150001;2.哈尔滨工程大学 航天与建筑工程学院，黑龙江 哈尔滨150001)

本文以高架起重机为例，研究了带有移动摆载荷柔性梁动力学问题.在工程实际中，结构承受移动载荷力学模型很普遍.Fung和Yau于2001年研究了旋转柔性梁在移动质量作用下的振动频率［1］，2002年用假设模态法研究了该系统的动响应.Lee在1996年用Lagarage法和假设模态法推导出悬臂梁在移动载荷作用下的动力学方程［2］.

Siddiqui在1998年研究了柔性梁在移动弹簧质量作用下的运动，利用Raileigh-Rits法和Perturbation法得出运动方程的近似解［3］.Ichikawa用模态分析法和直接积分法研究了多跨体连续梁在恒定速度移动质量作用下的动力学行为［4］.

由于交通工具质量增加及其运行速度的加快，许多研究人员关注结构和交通工具之间的相互作用，移动质量不能简化成一个质点而是一个移动的振荡器，在Fryba杰出的专著中对这一简单而又广泛涉及的例子列出了更多的建模和分析方法［5］.夏禾研究了简支梁在不同载荷作用下的振动分析［6］.彭献等研究了匀变速移动质量与简支梁耦合系统的振动分析［7］.本文在以上文献基础上，研究了移动摆载荷作用下柔性梁的振动问题，介绍柔性梁在移动集中力、移动简谐力和移动集中质量作用下的振动方程，基于Hamilton原理，推导出带有移动摆载荷柔性梁耦合运动微分方程，利用假设模态法对简支梁进行离散，采用纽马克逐步积分法对运动微分方程进行求解，本文所采用方法及推导的方程对工程实际问题研究有一定理论意义.

1 梁的振动分析

1.1 简支梁在移动力作用下的振动

如图1所示，忽略移动载荷质量，t=0时，常量力F位于左边支承处;某一瞬时常量力F移动到距左边支承点x=vt.假设简支梁为等截面(EI为常数)，单位长度质量为m，不考虑梁的阻尼.梁的运动满足小变形理论并在弹性范围内.对于移动小车质量与简支梁质量相比较小的情况，可将小车看作移动常力，给出其动力响应的近似解［8］:

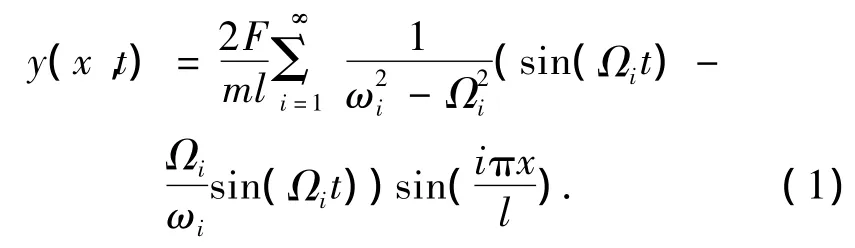
图1 匀速移动常力作用下的简支梁Fig.1 Simply supported beam subjected to a constant force moving at a constant speed

1.2 简支梁在移动简谐力作用下的振动

如图2所示，设简谐力F1cos(Ωpt)以匀速v通过简支梁.载重小车在简支梁上受到表面不平(跳车)的激励后，以小车的固有频率发生振动而通过简支梁时，小车簧上部分(即车身)的惯性力就是一种简谐力［9］.

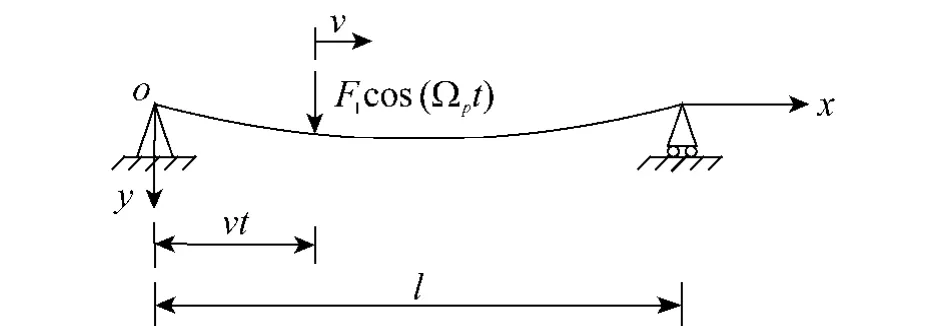
图2 匀速移动简谐力作用下的简支梁Fig.2 Simply supported beam subjected to a harmonic force moving at a constant speed

梁的动力响应为

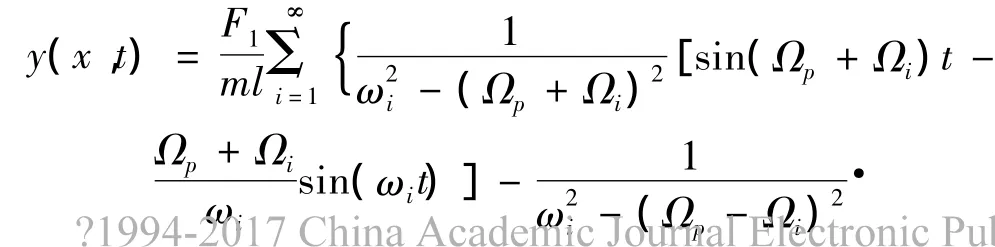
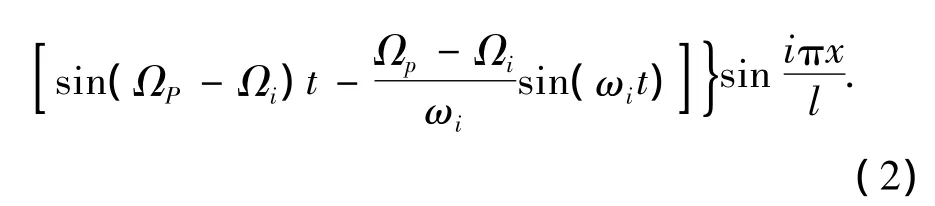
式中:Ωp为简谐力的挠动频率.

2 带有移动摆载荷柔性梁动力学方程

简支梁可以用Euler-Bernoulli梁来模拟，忽略了扭转和剪切变形的影响.起重载荷被简化为集中质量球摆，通过不可伸长且不计质量的绳子悬挂在沿柔性梁移动的小车上.

起重机的简化模型如图3所示，起重机小车的质量为mc，以速度x·c沿着柔性梁移动.刚性杆的长度为l，一端连接着小车，一端与摆载荷ml连接，刚性杆在垂直平面内的转角为θ.梁的杨氏模量为E，单位长度质量为m，长为lb，惯性矩为I.

图3 梁式起重机力学模型Fig.3 Mechanic model of a beam crane

设梁单元的位置矢量为rb，小车的位置矢量为rc，摆载荷的位置矢量为rL，可以表示为

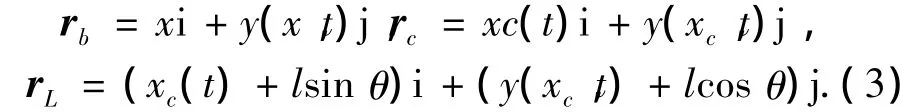
相应的速度矢量为

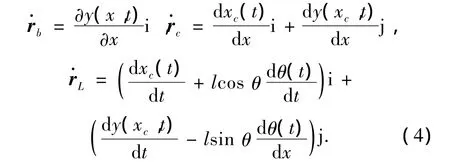
系统的动能T可以表示为

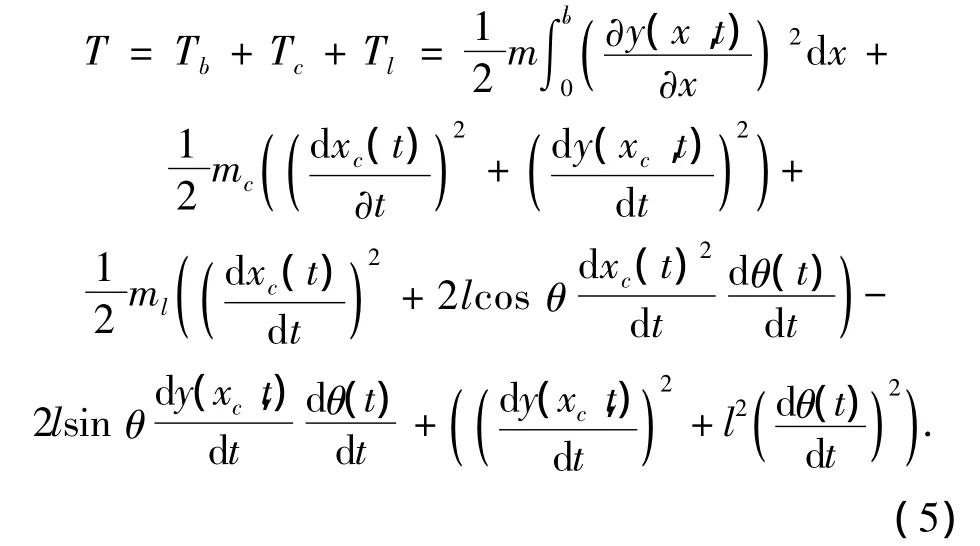
其中，Tb、Tc、Tl分别代表简支梁、小车和有效摆载荷的动能.

系统的势能为

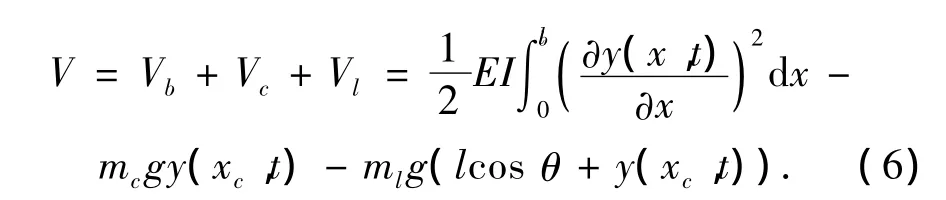
其中，Vb、Vc、Vl分别代表简支梁、小车和有效摆载荷的势能.

利用Hamilton原理可以推导出系统运动方程:

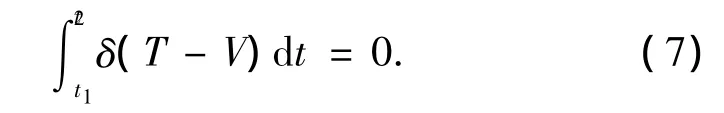
将式(5)、(6)代入式(7)得出下系统的非线性耦合运动方程:

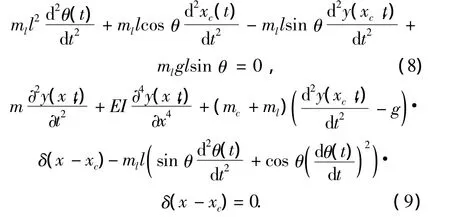
3 分析系统运动学方程

柔性梁耦合系统动力学模型如图4所示.

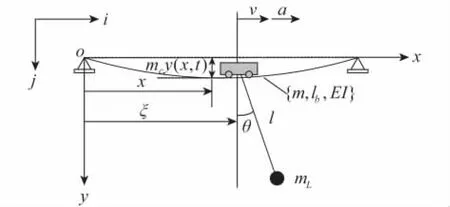
图4 移动摆载荷柔性梁耦合系统动力学模型Fig.4 Dynamic model of a flexible beam with a moving mass suspending a pendulum

已知小车质量mc，以初速度v0、匀加速度a向前运动，柔性梁单位长度质量m，抗弯刚度EI，梁上x处在t瞬时的挠度为y(x，t)，取小车位移方程ξ=，设

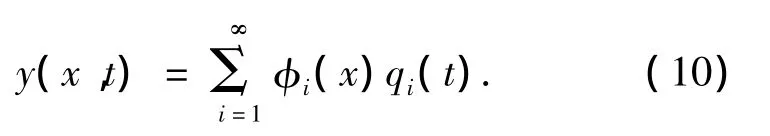
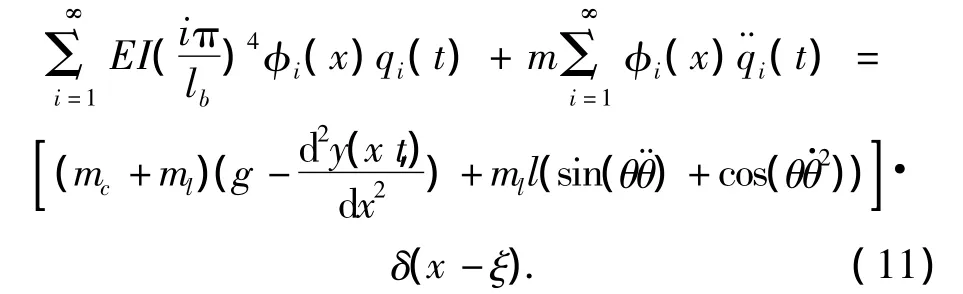
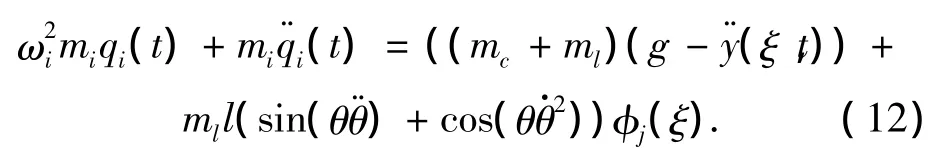
式中:mi为第i阶模态主质量，由

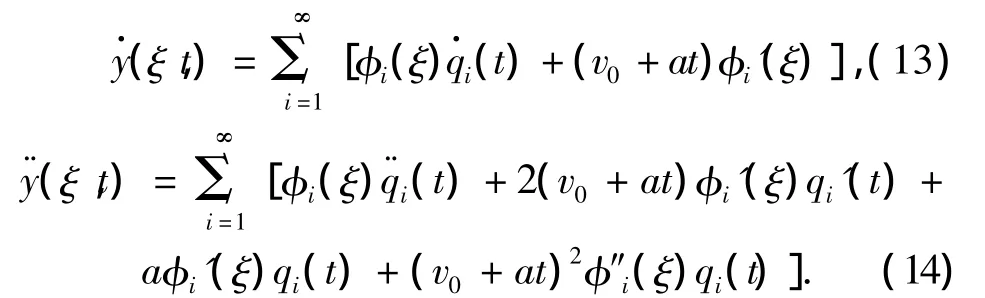
式(13)和(14)代入式(12)，得

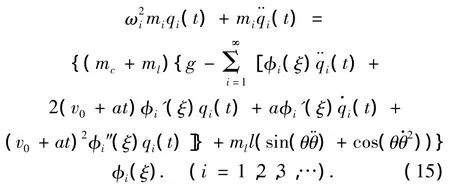
整理式(15)得

式(16)为有无穷多个变量且相互不独立的耦合动力学方程，因结构动力响应主要由若干个低阶振型起控制作用.对于复杂结构，采用振型分解法，计算中只取少数前几阶振型就可以获得满意的精度.对于简支梁位移级数取为N阶，则整个系统的自由度由无穷多个减少到N个，式(16)可写为N阶矩阵形式动力学方程

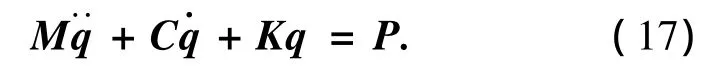
式中:

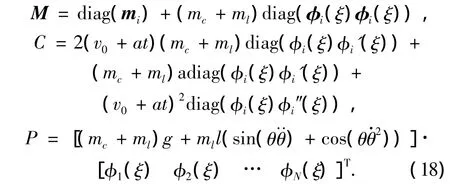
Φ(ξ)为模态函数矩阵，而Φ'(ξ)和Φ″(ξ)分别为Φ(ξ)关于ξ的一阶和二阶导数矩阵，M，C，K可进一步表示为

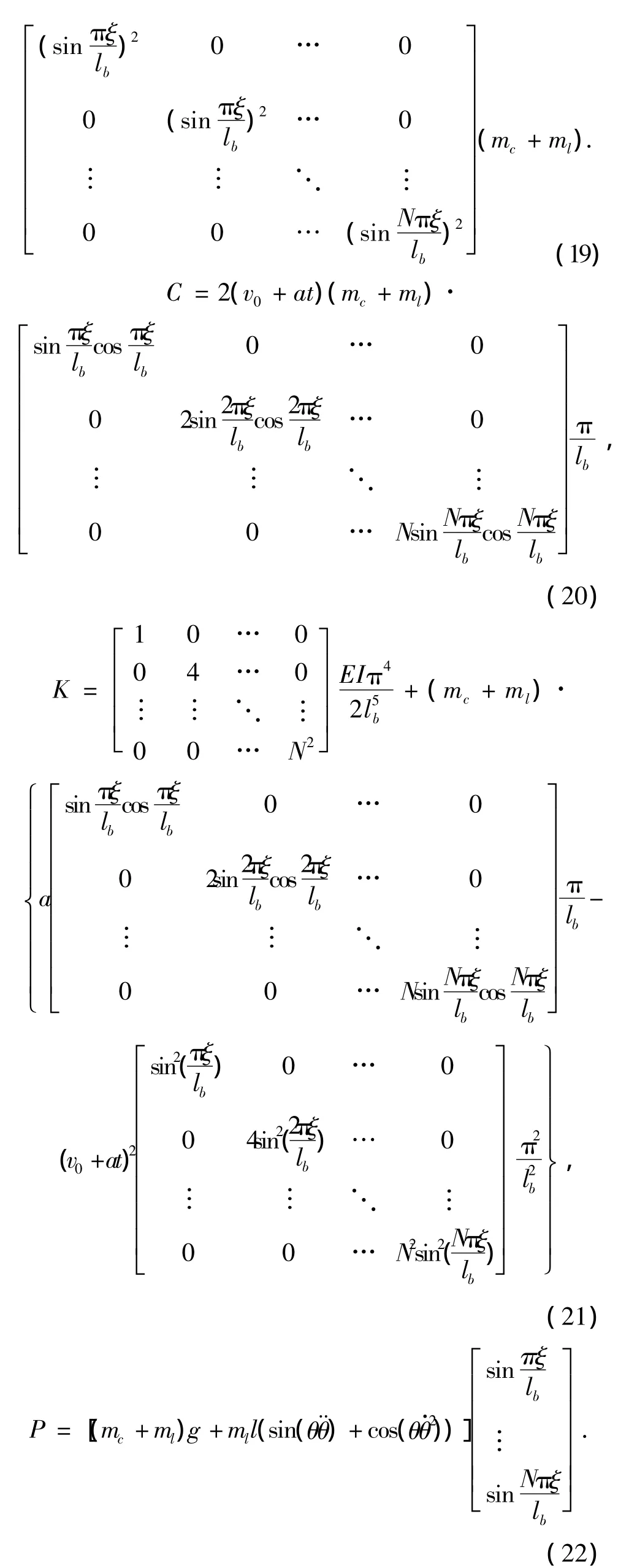
式中:θ=Asin(ωnt+θ0)，圆频率为

方程为二阶参数激励时变微分方程组，M、C、K、P均随时间t、运动参数v0、a而变化.采用nEWMARK逐步积分，可以求得各个时刻的q(t)，代入式(10)中得任意时刻梁上任意点的挠度.

4 动力响应及数值仿真

针对移动载荷不同匀速移动速度、不同加速度、不同摆载荷质量以及梁的自重等因素对梁中点位移挠度的影响进行了数值仿真.取积分时间步长dt= 0.01 s，参数γ=0.5，λ=0.25，小车质量和简支梁的参数mc=100 kg，I=0.1 m4，lb=20 m，E=2.15× 1011N/m2，仿真结果如图5～9所示.

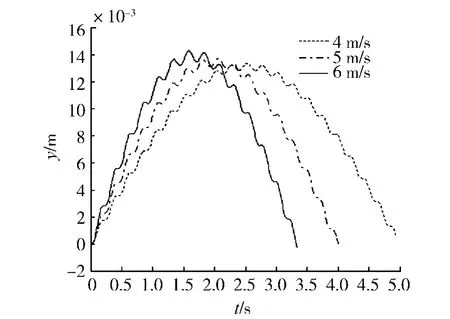
图5 不同移动速度梁中点挠度Fig.5 Midpoint deflection of beam in case of several moving speed

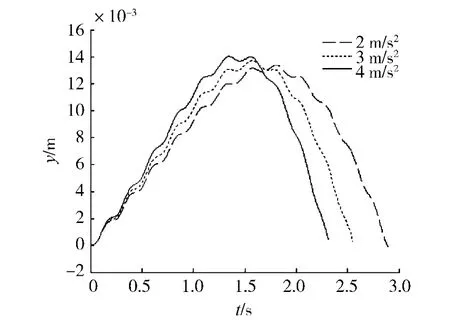
图6 不同匀加速移动速度梁中点挠度Fig.6 Midpoint deflection of beam in case of several moving acceleration

由图5可知，移动摆载荷的速度越大，梁中点挠度越大;由图6可知，在同一初速度v=4 m/s的情况下，移动质量加速运动时梁中点的挠度，比匀速运动时梁中点的挠度要大，且加速度越大，梁中点最大挠度越大;由图7可知，在同一初速度v=13 m/s的情况下，移动质量减速运动时梁中点的挠度，比匀速行驶时梁中点的挠度要小，且加速度的绝对值越大，梁中点最大挠度就越小，这与加速运动时恰恰相反.事实上，上述结果具有普遍规律，其力学解释是:当质量加速运动时，它受到梁给予的与运动方向一致的摩擦力，同时梁受到质量施加的反作用力，这个力可以看作是作用在梁上的轴向压力，该压力将在梁内产生附加弯矩，从而使梁的挠度加大.相反，当质量减速运动时，梁将受到轴向拉力，该拉力在梁内产生的附加弯矩使梁的挠度减小.

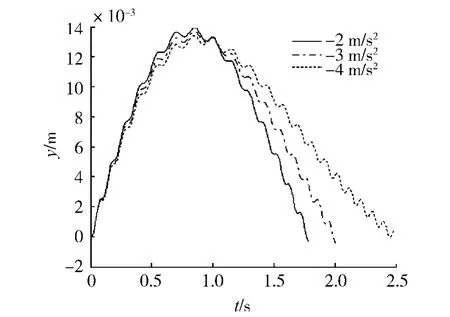
图7 不同匀减速移动梁中点挠度Fig.7 Midpoint deflection of beam in case of several moving deceleration

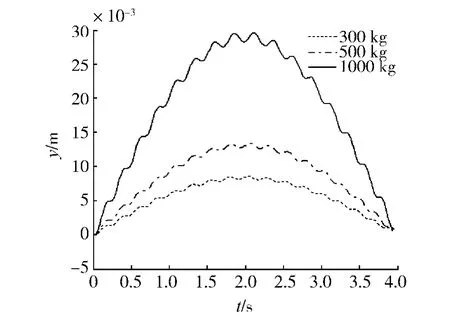
图8 不同摆载荷质量梁中点挠度Fig.8 Midpoint deflection of beam in case of several suspending mass load

图9 不同梁自重梁中点挠度Fig.9 Midpoint deflection of beam in case of several weight in a unit of lengh

由图8可知，摆载荷的质量越大，梁跨中的位移响应越大，振动越剧烈.由图9可知，梁单位长度的质量越大，其振动响应越剧烈，这一点吻合梁自由振动基本理论，由梁自由振动的固有频率可知，m越大，其频率ωi越小，振动响应越大.

5 结束语

本文从实际工程中的起重机出发，抽象出带有移动摆载荷柔性梁力学模型，讨论其在不同工况下承受移动摆载荷动响应，在其他参数一定的情况下，速度越大梁中点挠度越大.在同一初速度情况下，移动小车加速运动时梁中点挠度比匀速运动时梁中点挠度大，且加速度越大，梁中点最大挠度越大;而移动小车减速运动时梁中点挠度比匀速行驶时梁中点挠度小，且加速度绝对值越大，梁中点最大挠度就越小.其他条件不变情况下，摆载荷重量越大，梁跨中的位移响应越大.由于梁自重对振动频率的影响，单位长度质量越大，其振动响应越大.文中简支梁在不同工况和不同参数作用下的数值仿真结果，可用于实际工程优化设计.

［1］YAU D T W，FUNG E H K.Dynamic response of a rotating flexible arm carrying a moving mass［J］.Journal of Sound and Vibration，2002，257(1):107-117.

［2］LEE H P.Dynamic response of a Timoshenko beam on a Winkler foundation subjected to a moving mass［J］.Applied Acoustics，1998，55(3):203-215.

［3］SIDDIQUI S A Q，GOLNZRAGHI M F，HEPPLER G R.Dynamics of a flexible beam carrying a moving mass using perturbation，numerical and time-frequency analysis techniques［J］.Journal of Sound and Vibration，2000，229 (5):1023-1055.

［4］ICHIKAWA M，MIYAKAWA Y，MATSUDA A.Vibration analysis of the continuous beam subjected to a moving mass［J］.Journal of Sound and Vibration，2000，230(3): 493-506.

［5］FRYBA L.Vibration of solids and structures under moving loads［M］.3rd ed.London:Thomas Telford，1999:65-85.

［6］夏禾.车辆与结构动力相互作用［M］.北京:科学出版社，2002:140-153.

［7］彭献，刘子建.匀变速移动质量与简支梁耦合系统的振动分析［J］.工程力学，2006，23(6):25-29.

PENG Xian，LIU Zijian.Vibration analysis of a simply supported beam under moving mass with uniformly variable speeds［J］.Engineering Mechanics，2006，23(6):25-29.

［8］卢胜文.车桥耦合非线性振动研究［D］.天津:天津大学，2005:13-15.

LU Shengwen.Non-linear vibration study of coupled vehicle and bridge［D］.Tianjin:Tianjin Univesity，2005:13-15.