基于振速测量的HELS方法研究

杨德森，郭小霞，时胜国

(哈尔滨工程大学 水声工程学院 黑龙江 哈尔滨 150001)

20世纪80年代初，Williams等人提出基于空间声场变换(STSF)的近场声全息技术(NAH)，并证明了NAH技术在声源识别和定位方面的作用［1-3］;针对STSF对重建的声源表面形状要求严格的缺点，Kim和Lee等人提出基于边界元(BEM)方法的NAH，建立了任意形状声源的近场声全息理论，但是BEM存在特征频率处解的非唯一性问题，以及不同阶数的奇异积分问题［3-4］;针对这些缺点，Wu和 Wang提出Helmholtz方程最小二乘法(HELS)来实现对振动体外声辐射问题的分析［5-8］.HELS方法是另一种有效的声场重建方法，需要的测点数远远少于前面2种NAH方法要求的数量，这大大地提高了计算和工作效率.

这3种主流的近场声全息技术都是通过测量声压，进行声场重建和预测.而众所周知，振速作为声学量之一，也是值得关注的.尤其是随着矢量水听器的发展，可以同时测量声场中的声压量和质点振速分量，为研究振速量提供了简便的测量手段.

目前已经有学者对基于振速测量的重建特性进行了研究，Finn Jacobsen等人在声场变换算法的基础上，推导出基于质点振速测量的近场声全息重建公式，仿真研究表明在测量平面中基于声压测量的声压预报结果与基于质点振速测量的质点振速预报结果没有明显的区别，但是基于振速测量的声压重建较基于声压测量的振速重建要好得多，并且它较传统技术对于传感器失真不那么敏感［9］.张永斌等也用同样的方法证明了采用同样反映声场特征的质点振速来进行声场重建计算，有边缘重建精度高的特点而且还可以采用比声压小的全息面来获得同样的重建精度［10］.以上研究都是基于STSF方法，就是说这种基于振速测量的声场重建模型也存在对于外形不规则的声源，其应用的可靠性和精度会下降，重建的结果有时甚至会扭曲实际声场量的分布，不能准确反映物理事实.

由HELS方法振速模型的仿真研究可知［11］，振速模型能够更精确的重建声场中的声压量和振速量，但是从误差分析中可以看出重建振速量时，振速模型可以得到更高的重建精度，为研究声场中的振速信息提供更准确的量值.本文将着重研究基于HELS方法的振速模型用于重建声场中振速信息的性能，首先推导出基于振速测量的声场重建模型，然后通过仿真研究证明其重建振速时的重建精度大于声压模型，最后在仿真研究的基础上进行了湖上试验研究:运用8只矢量水听器组成线阵后扫描，得到发射换能器的空间声场分布的矢量信息进而计算得到声源位置.

1 基于振速测量的HELS原理

由理想流体介质中小振幅声波的波动方程，可以得到不依赖于时间变量的稳态声场的Helmholt方程:

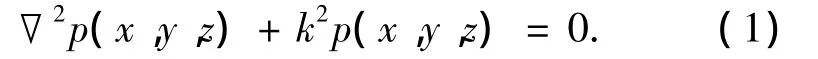
式中:p(x，y，z)为空间点(x，y，z)处的复声压，▽2为Laplace算子，k为波数.其中声压p满足3种类型的边界条件.利用第二类边界条件求解，可以近似表示为一组独立函数ψ的线性组合:

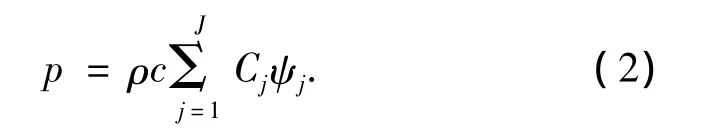
式中:ρ和c分别表示介质密度和介质中的声速，Cj为配置系数，ψj为基函数.

在球坐标系下，满足无限远处的Sommerfeld辐射条件:

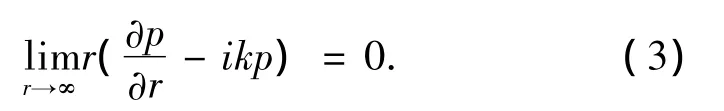
选取Helmholtz方程的特解——球面波函数为基函数:

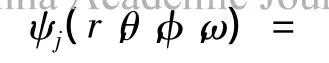
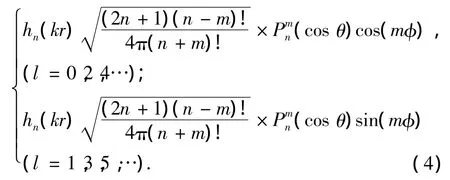
式中:hn(kr)表示球Hankel函数，Pmn(cos θ)表示连带Legendre函数［4］.

根据尤拉方程:

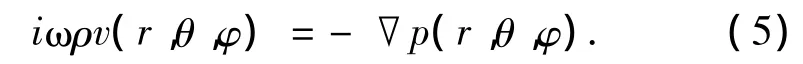
式中，v表示质点振速.

将线性表达式(2)代入方程(5)中得到:

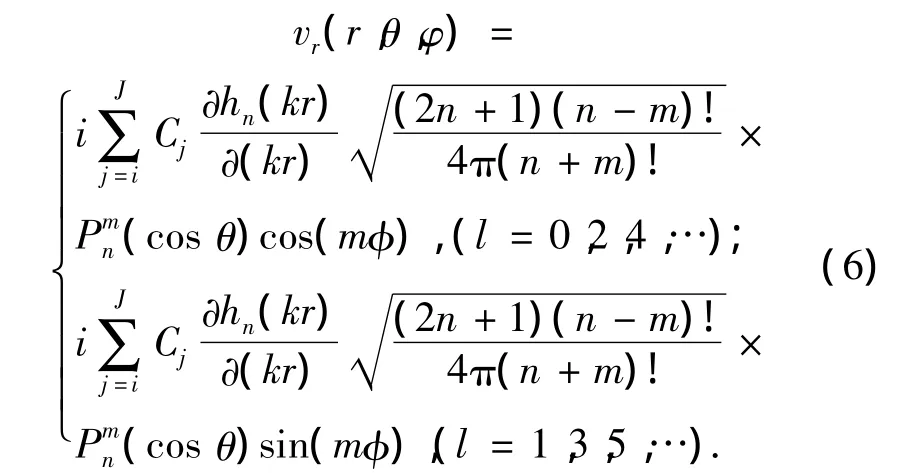
令ζ=kr，则得到球坐标系下径向振速的表达式:

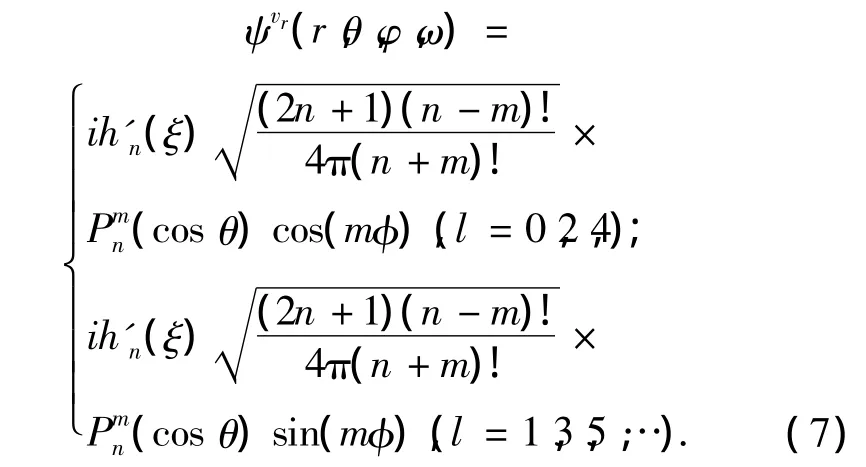
hn'(ζ)表示球汉克尔的导数.即得到了径向振速的重建公式:

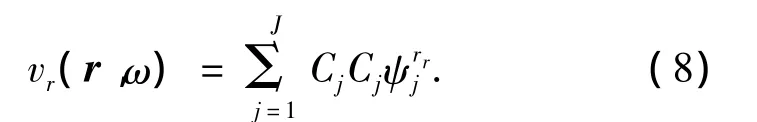
从声场重建式(2)～(8)的推导过程中没有近似，故结论是严格的，有其可行性.由式(8)可以看到，只要确定了基函数组ψvrj，也就获得了振速模型重建公式，能够解得系数Cj理论上就能够重建任意场点的振速值.

2 仿真参数的选取

HELS方法源于傅里叶级数，即将一个函数展开成有限个基函数的序列.如果要从测量值得到傅里叶级数，连续的傅里叶积分就必须离散化，这就引出了如何采样的问题.理论上空间采样要求传声器的间距必须小于或等于所感兴趣的最高频率对应的半波长，综合考虑本文分析声波的最高频率为1 000 Hz，水下试验中可实现最小阵元间距为: ΔDZ=0.75m≤λmin/2，试验中可操作最小测量距离Zm=0.85≪λmin，对于单极子声源仅仅需要J=4就可以完成声场重建.根据测量点数M与扩展函数个数J的关系:M≥1.4J，取M=7×8，形成矩形阵进行声场测量.

3 仿真算例及结果分析

为简单起见，选取点源作为仿真对象，其谐和球面行波场中各点法向振速的理论公式为

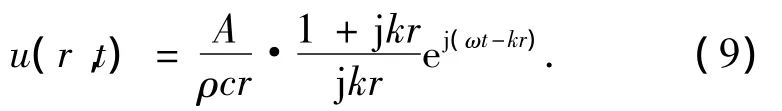
式中:A为利用边界条件求得的常数，在此取A=1，声源位于坐标原点.

图1、图2分别给出了声场中存在噪声时，声压和振速重建相对误差比较，可以看到基于振速测量的重建结果明显好于基于声压测量的重建结果.结果也显示了振速模型在重建效果方面的优势所在:振速模型的声场量重建结果同样随着噪声的增加而变差，但是其变化较声压模型缓慢，所以说振速模型对噪声的敏感性要好于声压模型.

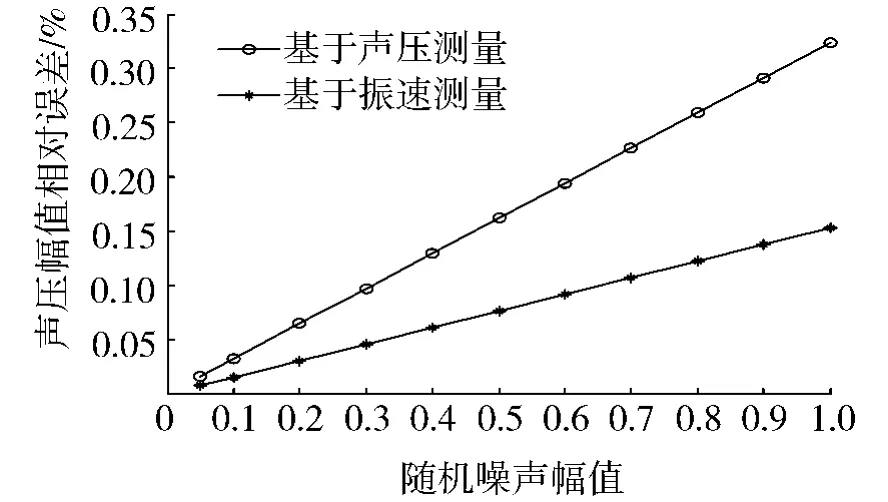
图1 声压重建误差比较Fig.1 The error comparison of reconstructed pressure

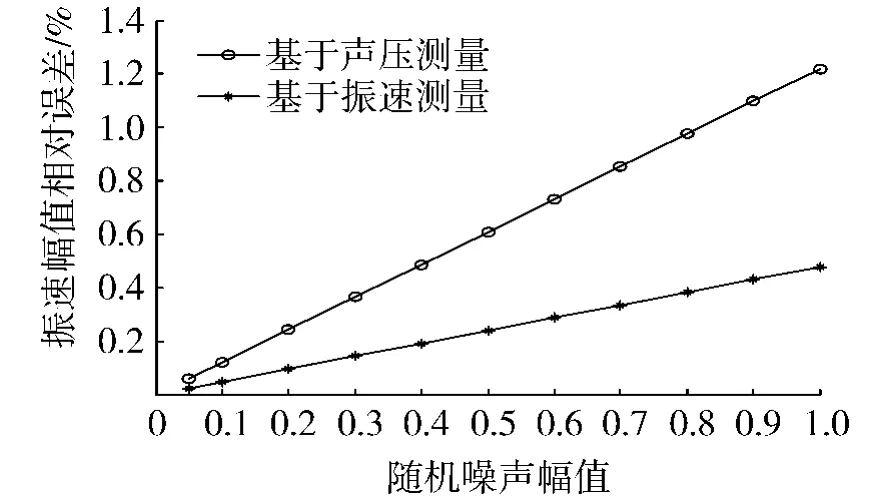
图2 振速重建误差比较Fig.2 The error comparison of reconstructed velocity

但是这些研究仅仅是在仿真条件下进行的，没有经过外场实验的验证，为了进一步确认该方法的工程应用性能，进行了湖上试验验证.

4 试验研究

4.1 单试验系统

声全息测量用的接收线阵是由8个胶囊形三维矢量水听器组成的线阵，相邻水听器间距为0.75 m，阵长为0.75×(8－1)=5.25 m.每个水听器分别用弹簧固定于圆柱形支架内，为了减小湍流对测量的影响，用丝袜将支架包裹，最后将安装好的8个小支架固定在基阵架上.

矢量阵基阵水平放置于z坐标轴，x坐标轴垂直于声源测量面，声源吊放位置到基阵之间的正横距离0.85 m，距离水面11.3 m.声源由基阵上方位置A开始以速度v=0.05 m/s作匀速直线运动，直到另一侧对称位置C停止运动，运动距离为L= 6 m，此时水平阵持续记录数据.对采样数据分段后，生成相对于声源运动的虚拟阵列数据，虚拟阵列沿相反方向运动形成面阵，面阵在运动方向的孔径为L.由于声源运动速度V=0.05 m/s，即马赫数Ma=2.6×10－5，所以运动对于测量数据的影响非常微小，也就是说多普勒效应可以忽略.

选定坐标系后(5号水听器为坐标原点)，声源的位置坐标为(y=0，z=－0.2).试验系统如图3、4所示.

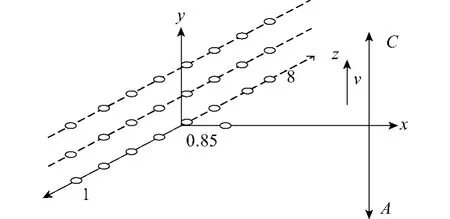
图3 试验坐标系Fig.3 The coordinate system of the experiment system

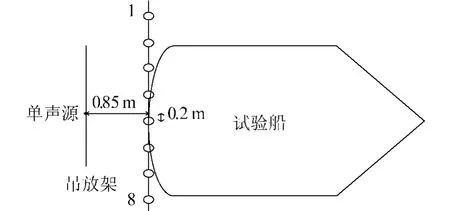
图4 声源位置俯视图Fig.4 The planform of the source position

声全息测量数据采集传输系统包括转接机箱、可编程滤波放大器6000、Pulse3560E，采集的数据直接保存到电脑硬盘，经过预处理后得到声场中声学量的重建值.

4.2 试验数据预处理

通过接收系统，最后得到的信号是正弦信号时域上离散的电信号采样值，而HELS方法的输入信号为声信号的频域值，可以看到要对接收到的信号进行一定的预处理才能够应用，则需要完成如下工作:1)对选定信号段进行相应的加窗窄带滤波，降低噪声的影响.2)根据矢量水听器各通道一致性校准的结果和测量放大器的放大量，对信号进行幅度修正，将电信号转化为声信号.3)将截取的整段数据分成7个小段，进行离散傅里叶变换后，获得该声源频率点的频域输入信号.4)最后根据各个虚拟阵元及真实阵元的扫描位置，进行排序构成HELS方法的输入数据.

4.3 试验结果分析

利用4.1节所描述的测量系统测得的数据后，根据4.2节给出的预处理方法对数据进行处理，再分别通过HELS方法的声压模型及振速模型对声场中的振速量进行重建，并与理论值对照分析重建振速幅值误差及声场中声源的定位误差.试验中根据法向振速的传播规律公式(9)，再利用测量得到的法向振速量，计算得到重建面的理论值.

4.3.1 单声源分析

由测量阵列步长决定了可分析声波的最高频率为1 000 Hz，则选取试验工况:按照1/3倍频程发射200～1 000 Hz的正弦声波，如图5、6所示(限于篇幅仅给出250 Hz与400 Hz典型声源声场的重建结果).

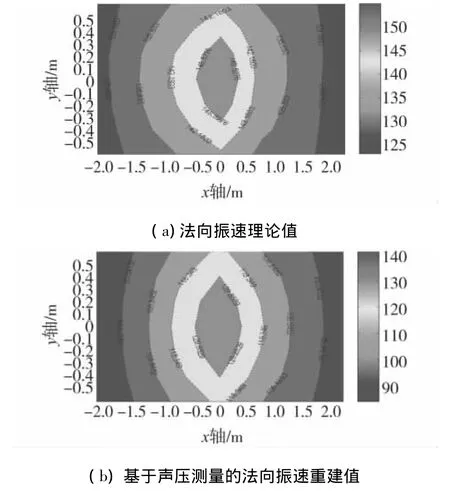
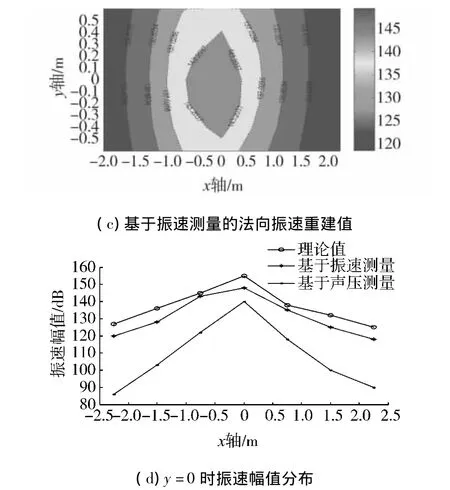
图5 法向振速重建结果比较(f=250 Hz)Fig.5 Comparison of reconstructed particle velocity at 250 Hz

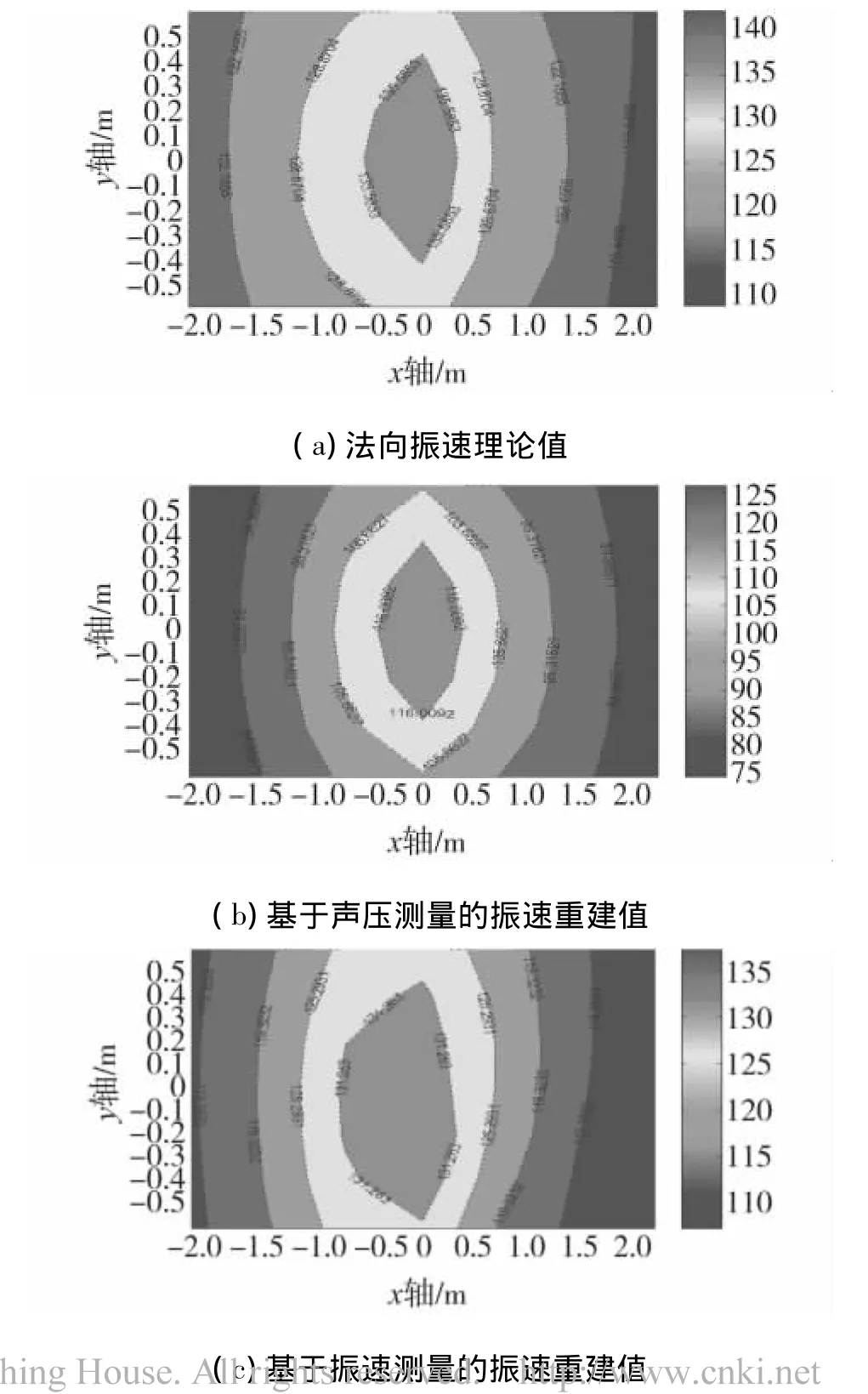
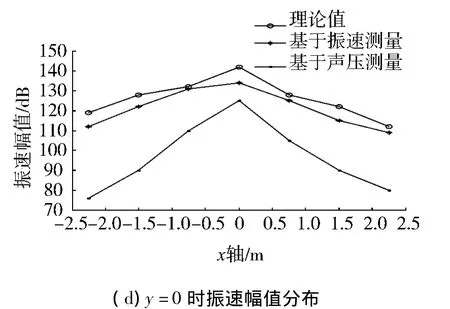
图6 法向振速重建结果比较图(f=400 Hz)Fig.6 Comparison of reconstructed particle velocity at 400 Hz

由图5、6可以看出虽然声压模型也可以较准确的重建声场中的法向振速值，但是其重建结果明显丢失了一部分细节信息，而且存在较振速模型大得多的幅值误差.另外，不论是振速模型还是声压模型都是重建面的中心区域误差小，边缘误差大，这是因为HELS方法是利用球面波近似声源的声辐射，在中心区域这种近似是较吻合的，而在边缘处这种近似相差最远，而且该方法本身的截断滤波也去除了说明边缘不连续性的高阶波数.

由声场重建模型可知，当测量模型一定时发射声波的频率也对声场重建精度有很大的影响，下面分析各工况法向振速声场的重建结果并计算不同频率时重建声源的幅值及定位误差.

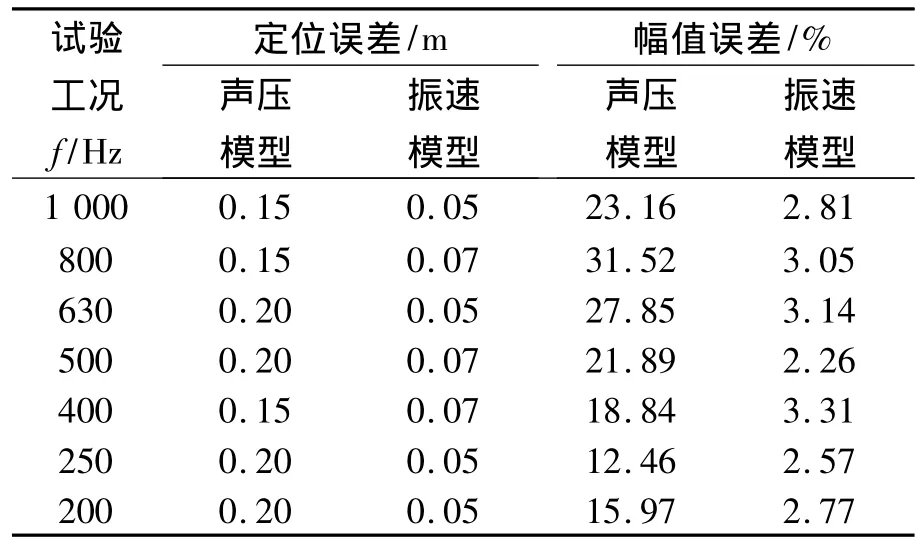
表1 不同频率声波的幅值误差与定位误差Table 1 Amplitude error and orientation error for different frequencies

由表中数值可以看出，在所选频率范围内振速模型和声压模型的性能很稳定，都能够得到较准确的法向振速重建值，而且定位误差与幅值误差的变化幅度都不大，与HELS方法低频适用性强的特点相符.从结果中也可以看出振速模型的重建结果明显优于声压模型，振速模型的幅值误差低于声压模型一个数量级，定位误差也明显小于声压模型.所以说重建声场中的振速量时，振速模型明显优于声压模型.

4.3.2 双声源分析

在实际工程中，有时也存在一些相干声源，对于该类声源HELS方法采取的措施是将几个声源包络在一个大的虚拟球面内看做单个声源进行声场重建，在虚拟大球面的外部可以得到声场的精确解.

利用两个发射换能器同时发射声波，共分析2个工况:声源频率为500 Hz和630 Hz，图7为数据处理之后得到的法向振速理论值与重建值.

可以看到在该工况下，声压模型和振速模型都不能准确重建2个声源的声场分布.

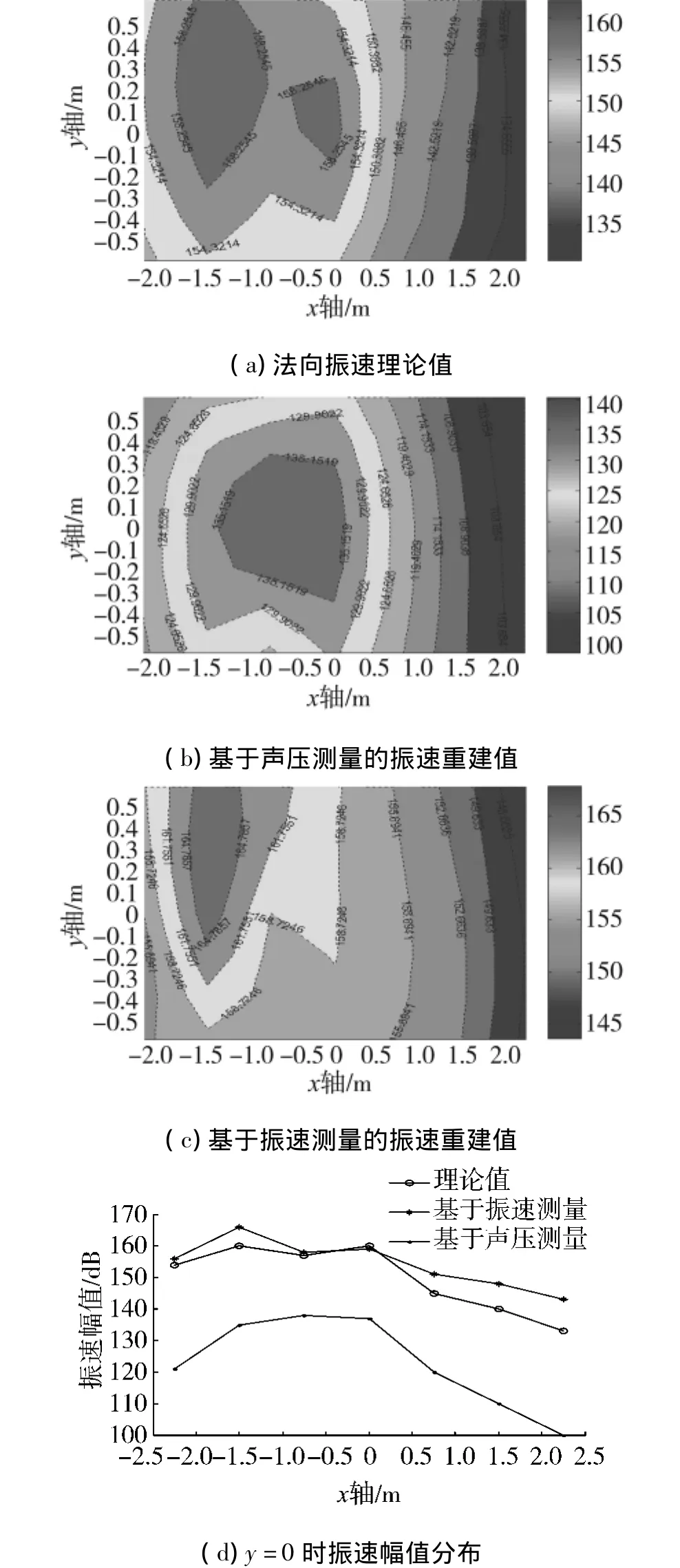
图7 法向振速重建结果比较图(f=500 Hz)Fig.7 Comparison of reconstructed particle velocity at 500 Hz

图8 法向振速重建结果比较图(f=630 Hz)Fig.8 Comparison of reconstructed particle velocity at 630 Hz

该工况下，振速模型能够清晰的分辨出2个声源的位置和相对大小，但是声压模型却已经失效.

可以看到2个模型重建相干声源声场的精度较单个声源稍差一些，但是振速模型的重建结果较声压模型能够更清晰地显示2个声源的位置及相对大小.同时也可以看出当频率增加时，虽然也能分辨出声源个数，但是声场的分辨率明显降低，且声压模型的重建结果与理论值相比存在明显的误差.这也是在意料之中的结果，因为2个声源排成一线可近似为长形声源，在HELS方法中，基于球Hankel函数构成的解析解最适合于声源表面形状接近1∶1∶1的声源，并能够在其最小球面内获得较高的重建精度，而对于长形声源重建精度稍差.

由试验结果可以看到:

1)利用声压模型重建声场中的振速量幅值误差偏大，由于环境噪声的影响使得声场重建存在幅值误差，所以该结果与仿真结果相吻合.

2)由于振速模型对于噪声的敏感性要低于声压模型，所以其确定的声源位置与实际声源的位置能够更好吻合，误差非常小，而声压模型确定的声源位置明显误差较大.

3)从不同频率声波的声场重建结果可以看出该模型比较稳定，能够较精确的对可测量范围内的声波完成声源定位及声场分析.

4)从相干声源声场的重建结果看出，当测量模型一定时，振速模型对于长形声源声场的重建也存在一定误差，但振速模型能够更清晰的识别声源.

5 结论

由传统HELS方法的基本原理出发推导出基于振速测量的模型，仿真分析了声场重建性能，设计湖上试验系统，并进行了结果分析，得出以下结论:

1)新模型同样具有实现过程简单，测点数目少和计算量小的特点，尤其它较声压模型有更高的声场重建精度.

2)证明振速模型对阵元位置误差及环境噪声的敏感性较声压模型低，能够更精确的确定声源的位置;在较低频率振速模型的频率适用性强，能够稳定且精确的对可测量范围内的声波完成声源定位及声场分析;同时对于相干声源的声场也能较准确的进行重建并识别声源个数及声源的位置信息.试验研究验证了振速模型用于水下声源识别定位的可行性和优越性，确定了该模型的工程应用前景.

［1］MAYNARD J D，WILLIAMS E G，LEE Y.Near-field acoustic holography.Ⅰ.Theory of generalized holography and the development of NAH［J］.J Acoust Soc Am，1985，78 (4):1307-1322.

［2］VERONESI W A，MAYNARD J D。Nearfield acoustic holography(NAH).Ⅱ.Holographic reconstruction algorithms and computer implementation［J］.J Acoust Soc Am，1987，81(5):1307-1322.

［3］何元安.大型水下结构近场声全息的理论与实验研究［D］.哈尔滨:哈尔滨工程大学，2000:71-91.

HE Yuanan.Theoretical and experimental investigation on near field acoustic holography of the large underwater structures［D］.Harbin:Harbin Engineering University，2000: 71-91.

［4］KIM G T，LEE B T.3-D sound source reconstruction and field reproduction using Helmholtz integral equation［J］.J Sound Vib，1990，136:245-261.

［5］WANG Z X，WU S F。Helmholtz equation least-squares method for reconstructing acoustic pressure field［J］.J Acoust Soc Am，1997，102(4):2020-2032.

［6］WU S F.On reconstruction of acoustic pressure fields using the Helmholtz equation least squares method［J］.J Acoust Soc Am，2000，107(5):2511-2522.

［7］ISAKOV V，WU S F.On theory and application of the Helmholtz equation least squares method in inverse acoustics［J］.Inverse Problems，2002，18(4):1147-1159.

［8］SEMENOVA T，WU S F.On the choice of expansion function in the Helmholtz equation least squares method［J］.J Acoust Soc Am，2004，117(2):701-710.

［9］JACOBSEN F，LIU Y.Near field acoustic holography with particle velocity transducers［J］.J Acoust Soc Am，2005，118(5):3139-3144.

［10］张永斌，毕传兴.基于质点振速测量的近场声全息技术［J］.农业机械学报，2007，38(9):112-116.

ZHANG Yongbin，BI Chuanxing.Near field acoustical holography study based on measurement of particle velocity［J］.Transactions of Chinese Society of Agricultural Mechaninec，2007，38(9):112-116.

［11］郭小霞，杨德森，时胜国.基于振速测量的HELS方法声场重建研究［J］.信号处理，2010，26(6):806-810.

GUO Xiaoxia，YANG Desen，SHI Shengguo.Helmholtz equation least squares method for reconstructing acoustic field with the measurement of particle velocity［J］.Signal Processing，2010，26(6):806-810.