深吃水半潜式平台垂荡响应数值分析

朱航，欧进萍

(1.船舶工艺研究所，上海 200032;2.哈尔滨工业大学 土木工程学院，黑龙江 哈尔滨 150090;3.大连理工大学 土木水利学院，辽宁 大连116023)

半潜式平台是坐底式平台和小水线面船概念相结合的结果.由于相对于Spar平台和TLP平台而言，半潜式平台初期投资较少，自20世纪60年代出现以来，半潜式平台在海洋油气的勘探开采中得以广泛的应用［1］.目前，半潜式平台已发展至第六代平台，有着适用工作水深广，抗风浪能力强，甲板空间大等众多优点.

但是，半潜式平台的缺点也很明显.半潜式平台的垂向运动较大，干树采油系统不能应用在其上，大大增加了作业成本与维护成本［2］.如何减小平台的垂荡响应，成为国内外学者研究的热点［3］，深吃水半潜式平台结构的概念也由此问世.深吃水半潜式平台的吃水深度往往在40 m左右，远大于常规半潜式平台的15～25 m吃水.另外，由于吃水较深，深吃水半潜式平台往往没有自我航行能力，平台的浮体常采用四方环形设计，这样可以更好地保证平台的稳定性.

吃水深度的增加很好地抑制了平台的垂荡响应，Bindingsb［4］的研究结果表明，与常规半潜式钻井平台相比，深吃水半潜式平台的垂荡及纵摇RAO可以减小50%左右.但是该作者在文中只说明了平台的吃水深度与排水量参数，且文中主要聚焦于立管的性能问题，对平台主体部分的研究不够.Youngpyo hong［5］等学者也研究了深吃水半潜式平台的浮体在浪、流联合作用下的涡激振动，他们的计算结果表明，浮体的涡激振动与波浪和海流的速度有着很大的关系.

J.Halkyard［6］对深吃水半潜式平台的结构进行了更大的改进，提出了DPS系列平台，其特点是在深吃水半潜式平台上增加了可收放的垂荡板，令平台的垂荡响应进一步减小.严格地说，DPS系列平台已经脱离了半潜式平台的特点，其结构原理和特点更与Truss-spar平台更为接近.DPS系列平台的垂荡板是缩进式的，可以收起至平台主体所围成的空间中，解决了平台运输方面的困难.

鉴于DPS系列的种种优点(附加垂荡板、缩进变形等)，其结构形式也许将成为未来深水半潜式平台的主流，下面针对DPS 2001-4平台，分析垂荡板对平台垂荡响应的影响，并对平台主体吃水深度的变化对平台垂荡响应所造成的影响进行研究，以更深入地对半潜式平台的结构形式进行改进.

1 DPS-4平台尺寸参数及锚泊系统参数

1.1 DPS 2001-4平台尺寸参数

图1为DPS 2001－4平台的结构示意图.该平台的设计水深为1 000 m，其水下结构可以包括主体水下结构与垂荡板2部分(连接桁架体积相比二者很小，因此不考虑).主体水下结构可以分为立柱和浮体:立柱共 4个，其截面尺寸为12.20 m× 12.20 m，柱中心的间距为48.40 m，浮体的宽度和深度为12.20 m;垂荡底板为3.05 m厚度的软仓，截面尺寸61.00 m×61.00 m，垂荡板中心处设置12.20 m×12.20 m的方孔以保证立管系统的顺利通过.平台主体吃水为61.00 m，垂荡板底部水深为97.60 m，图2为平台水下结构的数值模型.

图1 DPS 2001-4平台Fig.1 DPS 2001-4 deep draft semi-submersible platform

图2 平台水下结构数值模型Fig.2 Numerical model of DPS 2001-4 platform

1.2 锚泊系统参数

平台的锚泊系统由16根锚链组成，其中每4根锚链为一组，各分布于平台的一角，同组中相邻锚链的水平投影线夹角为5°，单根锚链为链－缆－链结构，3种材料的参数如表1.每根锚链的顶端与水平面的夹角为60.8°.

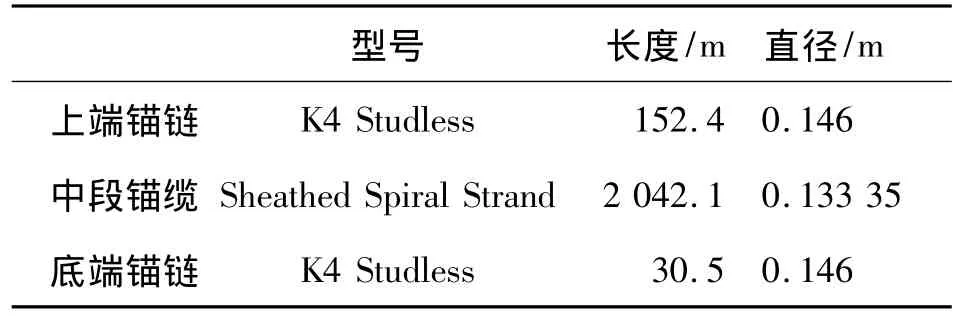
表1 锚链参数Table 1 Parameters of a mooring line

2 数值计算方法

DPS2001-4半潜式平台的垂荡运动方程可以表示为

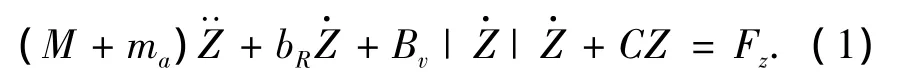
式中:M、ma和Br分别为平台质量、垂向附加质量和辐射阻尼，C为垂向刚度，Z为平台的垂向位移，Fz为平台的垂向激振力，它与固定平台上的波浪力相同.

2.1 垂向刚度计算

平台的垂向刚度包括静水回复刚度C1与锚泊系统的垂向回复刚度C2两部分，静水回复刚度C1与平台的水线面积S1有关，C1=Sγ，γ为海水容重.

锚泊系统的垂向刚度C2可采用分段外推－校正法［7］求解，其计算原理如下:

1)已知海水深度、锚链顶端与水平面的夹角θTop;

2)把锚链划分成若干个微段;

3)假设锚链顶端的拉力TTop已知;

4)计算每个微段上的重力和浮力;

5)建立微段的静力平衡方程(图3).

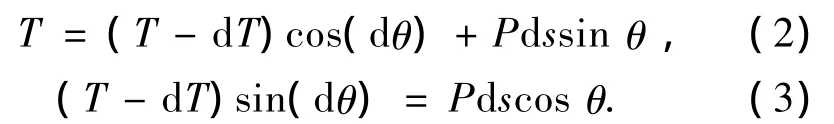
式中:T为微段顶端受到的拉力，P为单位长度的锚链受到的重力与浮力的合力，θ为微段顶端切线与水平方向的夹角，ds为微段的长度，dT和dθ分别为拉力和角度的变化量.考虑锚链微段的几何关系，有

其中，ε=T/(EA)为单位长度的锚链的伸长量，E、A分别为锚链的弹性模量和横截面积.通过式(4)和式(5)可求出锚链上任意一点的坐标值(x，z):

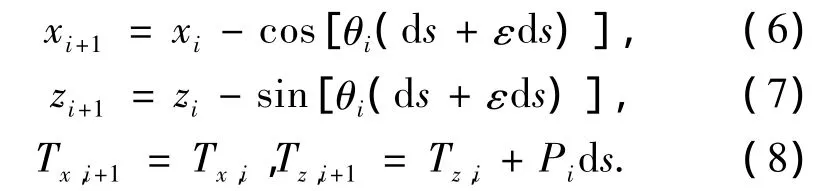
式(8)可得出下一段的水平力与竖直力，用于接下来的计算.

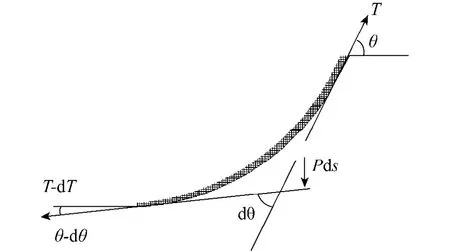
图3 锚链微段示意图Fig.3 Segment of the mooring line

最后验证锚链底端坐标zend的水深边界条件:如满足一定的精度，计算结束;如不满足，则返回3)，调整锚链顶端拉力TTop值的大小，重复计算.

在确定了TTop值的大小之后，锚泊系统顶端在竖直方向的拉力TTop，V

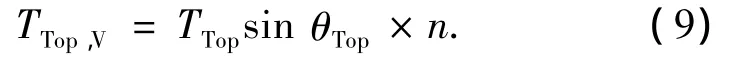
其中，n为锚泊系统中锚链的根数.

通过以上方法，得到锚链顶端拉力及其在竖直方向的分量.由于锚链顶端与水平面夹角为60.8°，可以确定锚链竖向拉力随平台垂荡响应的变化如图4.

图4的计算结果表明，平台锚泊系统的垂向刚度为非线性数值，其最大值为302 kN/m，与平台的静水垂向回复刚度比较，有

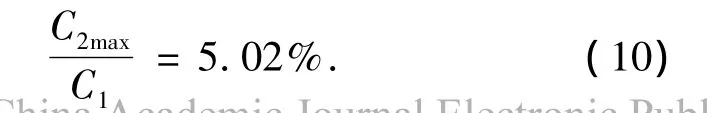
式(10)的计算结果表明:锚泊系统的垂向刚度最大值只有静水垂向回复刚度的5.02%，远小于平台的静水垂向回复刚度，因此，在平台的垂荡响应计算过程中，锚泊系统的垂向刚度将忽略不计.

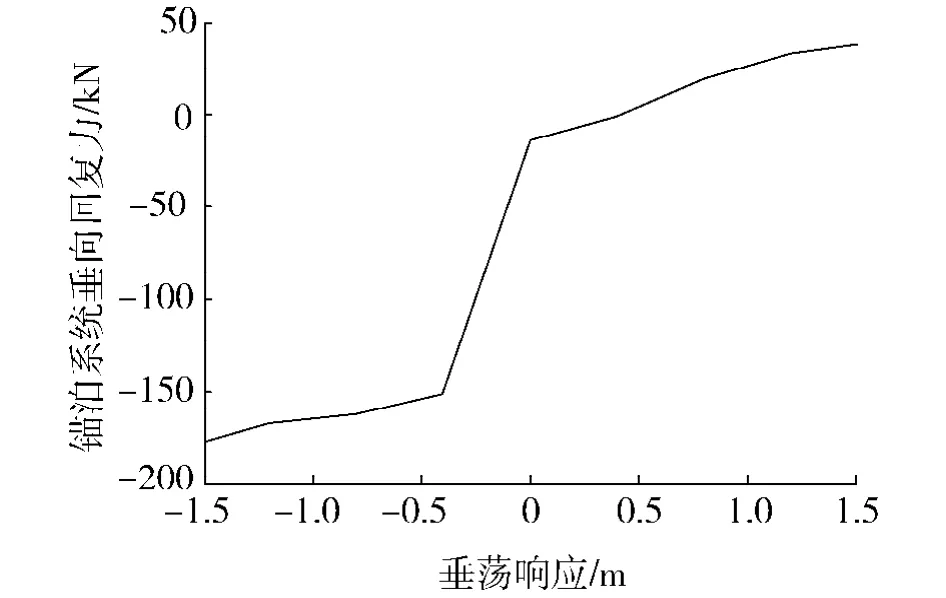
图4 锚泊系统竖向拉力随平台垂荡响应变化图Fig.4 Influence of the platform heave motion on the vertical force of the mooring system

2.2 阻尼系数计算

平台的阻尼可以分为粘滞阻尼与辐射阻尼2部分.粘滞阻尼可以用Bv||表示，Bv=ρSw［8］，Sw为平台的水下部分在垂向的投影面积(投影重叠部分需叠加，此处不考虑遮蔽效应).而平台的附加质量和辐射阻尼只与平台的振动频率ω相关.

2.3 平台的垂荡响应RAO求解

如假设式(1)中粘滞阻尼为0，则可简化为

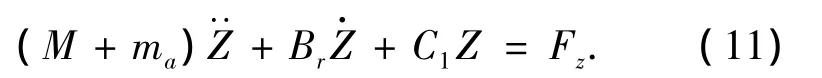
式(11)可以通过频域边界元理论［9］，求得平台各振动频率下的附加质量ma和辐射阻尼Br.

由于式(11)为简谐激励下的响应［10］，在振动频率为ω时，其稳态解的幅值可表示为

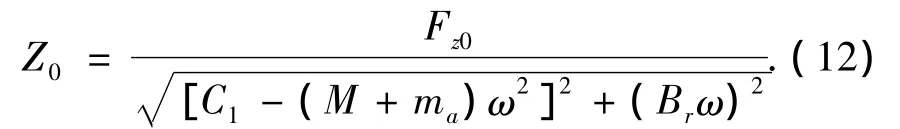
将与振动频率ω对应的附加质量、辐射阻尼重新代入式(1)，忽略锚泊系统的垂向刚度对平台垂荡响应的影响，并假设垂向激振力Fz与垂向位移Z为

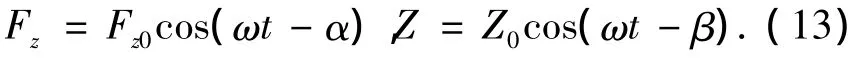
其中，Fz0和Z0分别为力和垂向位移的幅值.式(1)可变为

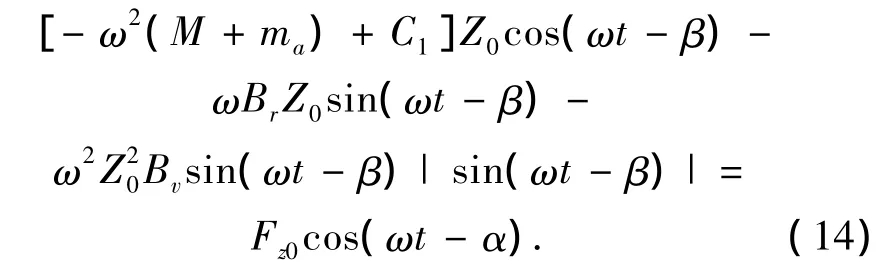
采用傅里叶级数展开，取第1项之后，sin(ωtβ)·|sin(ωt－β)|→8/3πsin(ωt－β)，式(14)可进一步变为

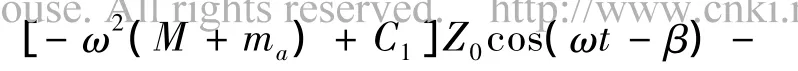
其中，(Br+8/3πωZ0Bv)即系统的等效阻尼，有

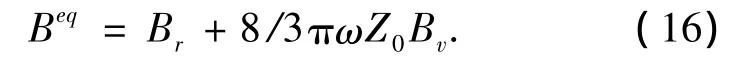
将式(16)代入式(1)，令M0=M+ma，有

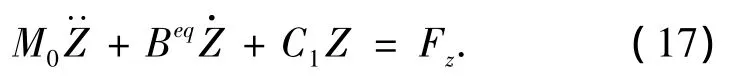
由于Fz与固定平台上的波浪力相同，其值只与入射波浪与平台外形相关.与式(11)对比，此处只有系统的阻尼发生了变化.由于式(17)同样为简谐激励下的响应，在振动频率同样为ω时，式(17)稳态解的幅值可表示为

可见，式(16)与式(18)组成了迭代循环，重复式(16)和式(18)，直至平台的振幅Zn与系统的等效阻尼满足计算精度.

这样，平台的RAO计算公式可表示为

其中，A为入射波的波幅.

3 计算结果分析

3.1 不同波浪入射角下平台的垂荡响应RAO比较

图5为各波浪入射角下平台的垂荡响应RAO结果，考虑平台的对称性，取波浪入射角为0°、15°、30°和45°进行分析.图5的计算结果表明，各波浪入射角下DPS 2004-1平台的垂荡响应RAO基本相同.也就是说，波浪入射角对平台的垂荡响应RAO基本无影响.因此，下面仅针对0°入射角时平台的垂荡响应RAO进行分析.

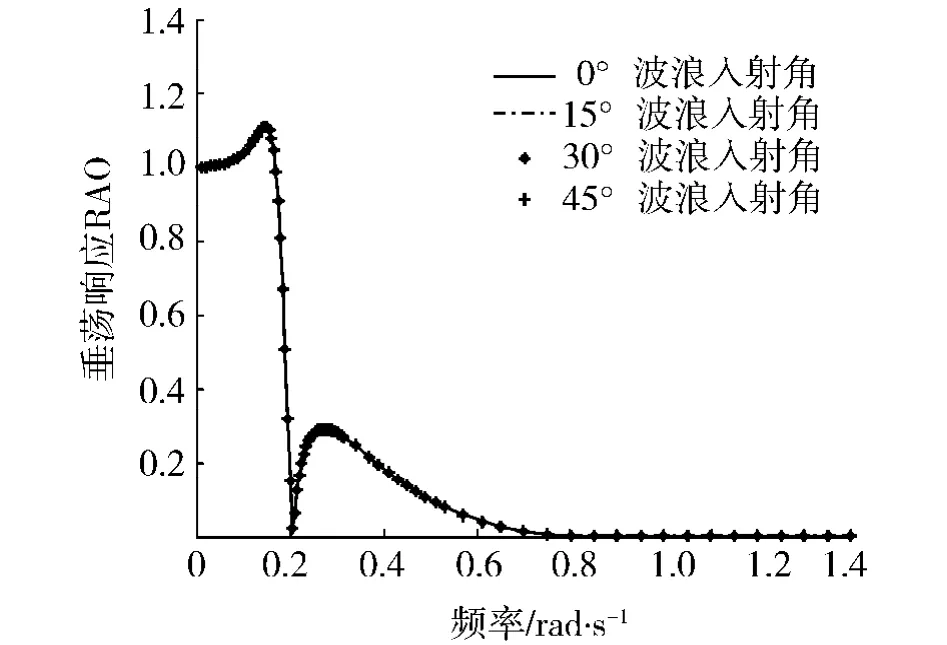
图5 各波浪入射角下平台的垂荡响应RAOFig.5 Platform heave motion RAO in different wave directions

3.2 粘滞阻尼与辐射阻尼比较

下面对粘滞阻尼与辐射阻尼的大小进行比较.图6为2种阻尼的比较结果.图6的计算结果表明:在垂荡响应RAO较大的频率段，即垂荡频率在0～0.4 rad/s频率范围内，平台的粘滞阻尼远大于辐射阻尼.即使是在其余垂荡响应RAO较小的振动频率段，粘滞阻尼也不小于辐射阻尼，这说明，粘滞阻尼在总阻尼中占主要部分.

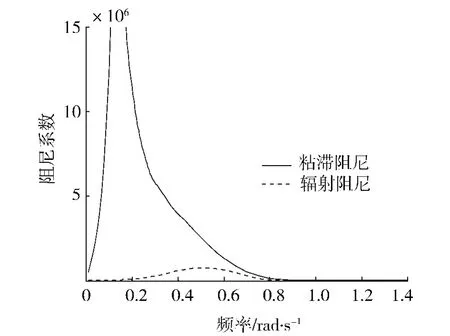
图6 粘滞阻尼与辐射阻尼的比较Fig.6 Comparison of the viscous damping and radiation damping

3.3 垂荡板对平台垂荡响应RAO的影响

为了研究垂荡板对平台垂荡响应RAO的影响，图7对比了DPS2001-4平台与主体相同的常规深吃水半潜式平台的垂荡响应RAO.图7的计算结果表明，与常规深吃水半潜式平台相比，DPS 2001-4平台的垂荡响应RAO的自振频率段进一步远离了海洋波浪主频段，达到了更好的垂荡减振效果.这说明垂荡板对平台的垂荡响应有着很好的抑制作用.

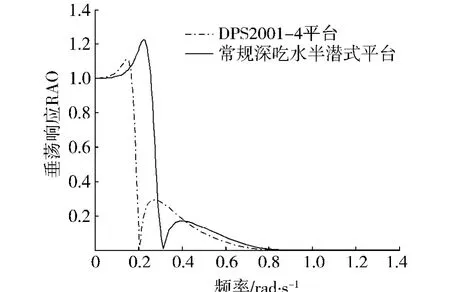
图7 垂荡板对平台响应垂荡RAO的影响Fig.7 Influence of the heave plate on platform heave motion RAO

3.4 垂荡板放置深度对平台垂荡响应的影响

下面研究垂荡板放置水深对平台垂荡响应的影响.图8为平台主体结构相同、垂荡板水深位置不同时，平台垂荡响应RAO的比较.图8的计算结果表明:随着垂荡板放置水深的增加，平台的垂荡响应RAO在低频范围幅值略有增加，而在波频范围幅值则略有下降.总的来说，垂荡板放置水深对平台垂荡响应RAO略有影响，但是影响较小.

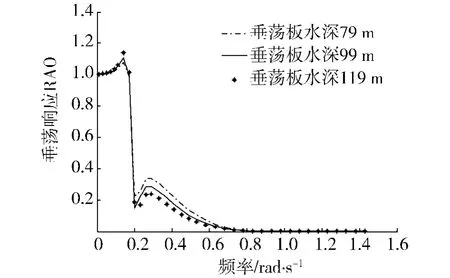
图8 垂荡板放置深度对平台垂荡响应RAO的影响Fig.8 Influence of the heave plate draft on platform heave motion RAO

为了进一步说明垂荡板放置深度对平台垂荡响应的影响，下面比较各海域百年一遇海况下不同垂荡板深度时平台的垂荡响应极值［11］，海况的选择如表2.

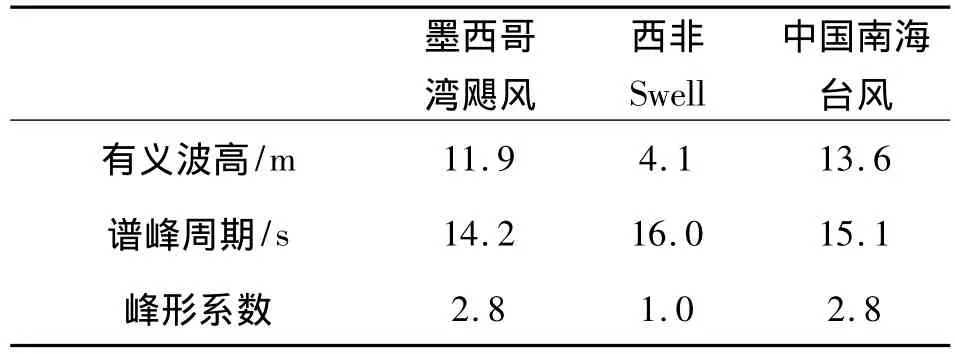
表2 极端海况Table 2 Extreme sea environment

平台在各海况下的垂荡响应极值计算方法如下.

首先计算平台各海况下的垂荡响应谱.在响应谱分析中，波浪谱选择为五参数的JONSWAP波能谱，其表达式为［12］

式中:α=5.058［Hs/(Tp)2］2(1－0.287lnγ)为广义菲利普常数;σ为谱宽常数，当ω＜ωp时，σ=0.07，而当ω＞ωp时，σ=0.09.

平台的垂荡响应谱为

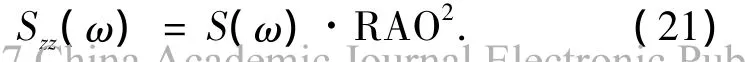
随机波浪条件下的平台垂荡响应极值Xmax的计算公式为［13］

其中，σx和v0分别为平台垂荡响应谱Xzz(ω)的标准差和过零率.二者的计算公式分别为

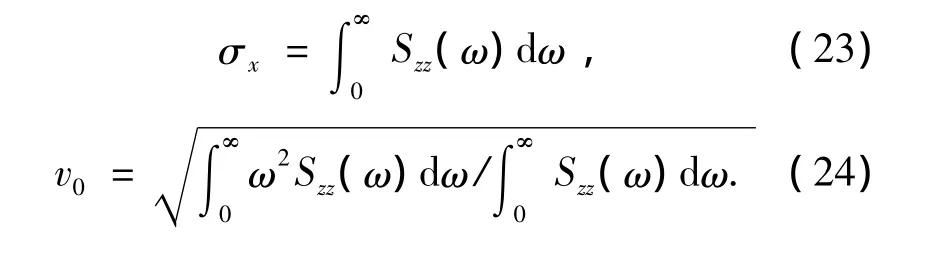
图9为各海域百年一遇海况下平台垂荡响应极值，图9的计算结果表明:随着垂荡板放置水深的增加，平台在各海况下的垂荡响应极值逐渐变小，但是这个减小的趋势逐渐变缓.当垂荡板吃水深度超过100 m后，下降的趋势变得更加缓慢，以至于此时中国南海台风海况和西非Swell海况时平台的垂荡响应极值趋于恒定值.这也表明DPS 2001-4平台的垂荡板水深位置是合理的.按照DPS 2001-4平台的垂荡板吃水水深99 m考虑，平台在三种海域百年重现期海况下，垂荡响应极值均不超过2 m，这表示干树采油系统可以在平台上使用，这将极大的提高平台的经济性.

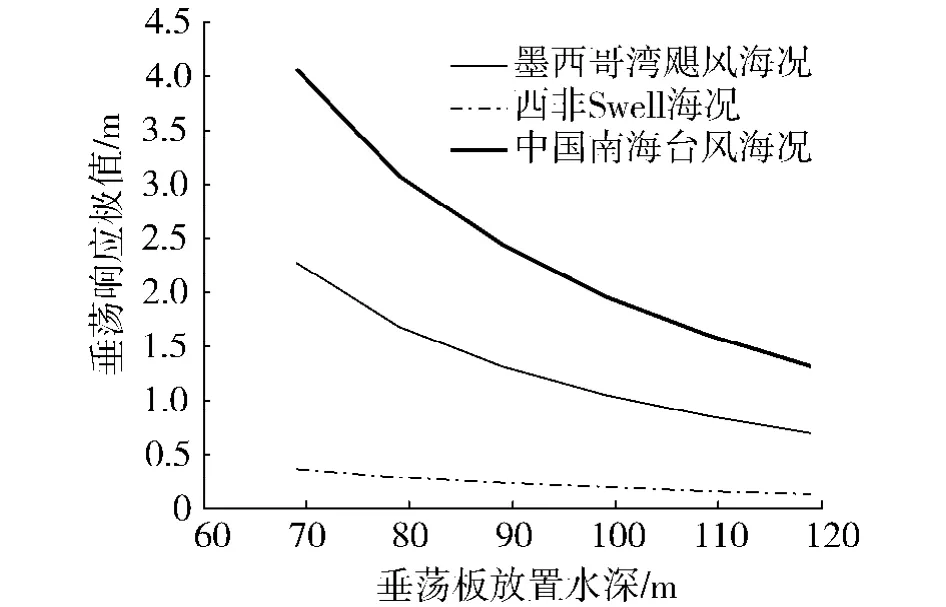
图9 垂荡板放置深度对平台垂荡极值的影响Fig.9 Influence of the heave plate draft on the platform heave motion extremes

4 结论

将平台的粘滞阻尼线性化处理，通过数值迭代的方法得到了平台的垂荡响应幅值算子(RAO)，并根据得到的幅值算子(RAO)求得了平台在3种海域下的垂荡响应极值，得到结论如下:

1)在DPS 2001-4平台的垂荡响应计算中，其垂向刚度以平台的静水垂向回复刚度为主，而阻尼则以粘滞阻尼为主.

2)垂荡板对于减小平台的垂荡响应有着重要的作用，当垂荡板下放到指定水深后，与主体相同的常规深吃水半潜式平台相比，DPS 2001-4平台的垂荡响应自振频率段进一步远离了海洋波浪的主要频率段，达到了更好的垂荡减振效果.

3)平台的垂荡响应极值随着垂荡板的放置水深的增加而减小，但是这个减小的趋势逐渐变缓.垂荡板的放置水深应根据平台的性价比而进行合适的选择.

［1］刘海霞.深海半潜式钻井平台的发展［J］.船舶，2007，6 (3):6-10.

LIU Haixia.Development of deep-sea semi-submersible drilling unit［J］.Ship and Boat，2007，6(3):6-10.

［2］杨立军，肖龙飞，杨建民.半潜式平台水动力性能研究［J］.中国海洋平台，2009，24(1):1-9.

YANG Lijun，XIAO Longfei，YANG Jianmin.Review on the study of hydrodynamics of semi-submersible platforms［J］.China Offshore Platform，2009，24(1):1-9.

［3］CERMELLI C A，RODDIER D G，BUSSO C C.Minifloat:a novel concept of minimal floating platform for marginal field development［C］//Proceedings of the 14th International Offshore and Polar Engineering Conference. Toulon，France，2004:538-545.

［4］BINDINGSBO A U.Deep draft semi-submersible［C］// Proceedings of the 21st International Conference on Offshore Mechanics and Artic Engineering.Oslo，Norway，2002: 651-659.

［5］YONGPYO H，YONGHO C.Vortex-induced motion of a deep-draft semi-submersible in current and waves［C］// Proceedings of the 18th International Offshore and Polar Engineering Conference. Vancouver， Canada， 2008，453-459.

［6］HALKYARD J，CHAO J，ABBOTT P.A deep draft semisubmersible with a retractable heave plate［C］//Offshore Technology Conference Proceedings.Houston，USA，2002.

［7］滕斌，郝春玲.Chebyshew多项式在锚链分析中的应用［J］.中国工程科学，2005，7(1):21-26.

TENG Bin，HAO Chunling.Numerical simulation of static behavior of the single anchor cable［J］.Engineering Science，2005，7(1):21-26.

［8］李彬彬，欧进萍.Truss Spar平台垂荡响应频域分析［J］。洋工程，2009，27(1):8-16.

LI Binbin，OU Jinping.Heave response analysis of Truss Spar in frequency domain［J］.The Ocean Engineering，2009，27(1):8-16.

［9］李玉成，滕斌.波浪对海上建筑物的作用［M］.2版.北京:海洋出版社，2002:63-75.

LI Yucheng，TENG Bin.Wave action on maritime structures［M］.2nd ed.Beijing:China Oean Pess，2002:63-75.

［10］胡宗武.工程振动分析基础［M］.上海:上海交通大学出版社，1999:44-50.

HU Zongwu.Fundamentals of engineering vibration analysis［M］.Shanghai:Shanghai Jiaotong University Press，1999:44-50.

［11］李彬彬，欧进萍.新型深吃水立柱平台在极端海况下的动力性能分析［C］//第六届全国土木工程研究生学术论坛，北京，2008:186-191.

［12］SUBRATA C.Handbook of offshore engineering［M］.Amsterdam:Elsevier，2005:427-437.

［13］DAVENPORT A G.Note on the distribution of the largest value of a random function with application to gust loading［J］.ICE Proceedings，196l，28(2):187-196.