一种新的双基地MIMO雷达收发角和多普勒频率联合估计方法

吴跃波 郑志东 杨景曙

(解放军电子工程学院 合肥 230037)

1 引言

MIMO雷达是目前国际上的研究热点，按其收发阵元的配置方式可分为：空间分集MIMO雷达[1]和单(双)基地雷达[2−11]。单(双)基地 MIMO 雷达采用紧密布阵方式，便于实现对目标的角度估计，且能形成大的虚拟阵列孔径，提高角度分辨力，以及增加目标可定位数量[2]。本文研究的是双基地MIMO雷达对多目标的收发角和多普勒频率估计联合估计方法。

现有的单(双)基地MIMO雷达参数估计大都是针对静止目标或假设已知目标多普勒频率，而仅对目标的角度进行估计。例如，文献[3]研究了Capon,APES, CAPES和GLRT等MIMO雷达角度估计算法，文献[4-9]研究了MUSIC, ESPRIT，降维Capon,传播算子和多项式求根等 MIMO雷达角度估计方法。对双基地MIMO雷达收发角和多普勒频率联合估计的研究很少，仅有文献[10,11]对此进行了研究。文献[10]利用矩阵的双正交性构造合理的代价函数，通过多阶段分解依次估计每个目标的收发角和多普勒频率，能够消除发射信号不满足理想正交对目标定位精度的影响。它的主要缺点是算法复杂且运算量较大，对每个目标的角度和多普勒频率估计都需要大量迭代，且每次迭代都需要多次特征值分解。文献[11]基于 PARAFAC先构造出接收信号的三面阵模型，然后采用三线性交替最小二乘法(TALS)对目标的收发角和多普勒频率进行估计，算法简单快速。由于散射系数通常未知，因此该方法实际上只能对Swerling I目标进行估计。经仿真发现，该方法的缺点是估计结果不稳定，时常出现估计误差较大的现象，即便增加迭代次数仍无法消除。针对已有算法的不足，本文提出了一种新的双基地MIMO雷达收发角和多普勒频率联合估计方法，算法简单易懂、运算时间少且参数估计精度高。

本文的结构安排如下：第 2节给出双基地MIMO雷达匹配滤波器输出的信号模型；第3节推导目标多普勒频率矢量、接收角矢量和发射角矢量的提取过程；第4节提出收发角和多普勒频率联合估计的算法流程；第5节通过计算机仿真和文献[11]进行对比，表明本文算法的优势；第6节为结束语。

2 信号模型

如图1所示，MIMO雷达发射阵列和接收阵列均采用等距均匀线阵，共有M个发射阵元，N个接收阵元，发射阵元间距和接收阵元间距分别为dt,dr。

图1 双基地MIMO示意图

在已知的同一距离分辨单元上目标存在P个目标，第p个目标的发射角、接收角及多普勒频率分别记为 φp,θp,fdp。各发射阵元同时发射相互正交的脉冲串信号，第m个发射阵元发射的第l个脉冲为

式中t和t′分别对应慢时间和快时间，T表示脉冲重复周期。sm(t)表示第m个发射阵元的基带信号。则第n个接收阵元接收到的第l个脉冲回波为

式中n=1,… ,N;l=1,… ,L,wn,l(t)为噪声， τ 为第1号发射阵元到目标再到第1号接收阵元的时延。αlp为第p个目标在第l个脉冲的散射系数，认为目标是慢起伏的，即在L个脉冲内对应的散射系数相同：αlp=αp。补偿时延τ 后，可得

假设发射信号的正交性对目标的多普勒频率不敏感，即

对yn,l(t)进行M组的匹配滤波，第m组的滤波输出为

其中认为wn,m,l为零均值，方差2σ的复高斯随机变量，对于不同的n,m,l互相独立。总共可获得NML个滤波输出结果。

3 多普勒频率矢量和收发角矢量的提取

本节将利用匹配滤波输出结果的特点，分别提取P个目标的多普勒频率矢量、接收角矢量和发射角矢量，为第4节的算法做准备。

3.1 对多普勒频率矢量的提取

对于第l个脉冲，将n=1,… ,N;m=1,… ,M的滤波输出列成一个MN维的列矢量，可得

其中

其中vl=Bwl，均值为零。

令目标的多普勒频率矢量为cf=[ej2πfd1T…ej2πfdPT]T，由式(8)，则对于第l+1个脉冲可得

联立式(8)和式(9)可得

注意到，第 1个噪声项diag(cf)vl的能量与v相同，两项噪声独立且均值都为l零。因此，为了获取多普勒频率矢量cf，依据式(10)，可求解如下优化问题：

令bl=Byl,式(11)写为

令 βp=2πfdpT，式(12)的解可通过如下等式获得

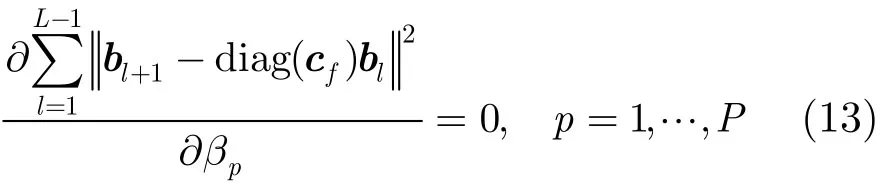
由式(13)可解出

其中cf,p表示矢量cf的第p个元素，bl,p表示矢量bl的第p个元素。由式(14)可得目标的多普勒频率为

3.2 对接收角的提取

对接收角矢量的提取和对多普勒频率矢量的提取类似。对于第n个接收阵元，将l=1,…,L;m=1,… ,M的滤波输出列成一个LM维的列矢量，可得

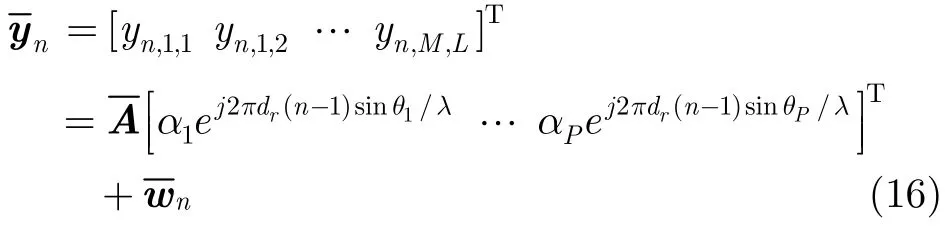
其中

则对接收角矢量的提取归结为如下优化问题：

解出

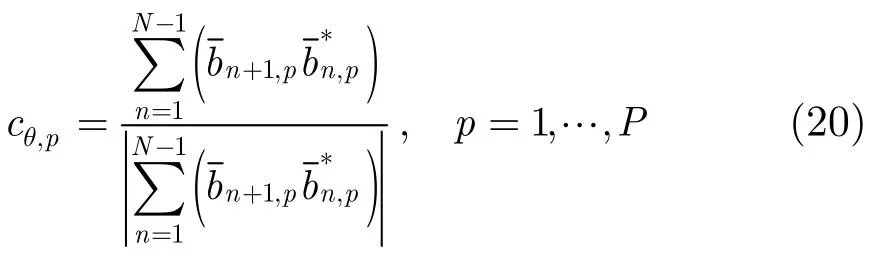
其中cθ,p表示矢量cθ的第p个元素，bn,p表示矢量bn的第p个元素。则目标的接收角为

3.3 对发射角的提取

同样地，对于第m个发射阵元，将l=1,…,L;n=1,… ,N的滤波输出列成一个LN维的列矢量，可得

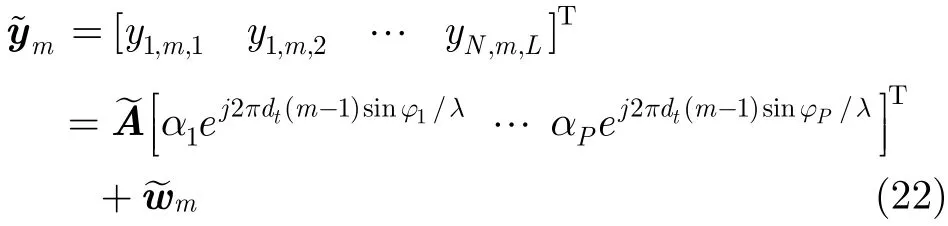
其中

其中cφ,p表示矢量cφ的第p个元素，,p表示矢量m的第p个元素。目标的发射角为

4 算法流程

上一节中对目标的多普勒频率和收发角进行了提取，由式(14)，式(20)和式(24)可见，对某个量提取的结果和另外两个量是有关的。因此为了获得目标的多普勒频率和收发角，应采用迭代算法，具体流程为：

步骤1 随机初始化P个目标的收发角和多普勒频率

文献[11]采用 TALS法每次迭代的主要运算量都是伪逆的运算，运算量和本文算法相当。但文献[11]每次迭代需要串行3步才能完成估计的更新，而上述本文算法每次迭代可并行一步完成估计的更新，因此本文算法的一次迭代运算时间小于 TALS的一次迭代运算时间，大约是其三分之一。此外，由于在同一次迭代中完成，相同的序号对应到同一个的目标，故本文算法估计的参数也可自动配对。

算法流程步骤4中的迭代终止的条件可以选用(或选用它们的与或组合)：

(1)迭代次数达到给定的上限；

(2)误差ε达到给定的下限；

(3)当前误差和上次迭代误差的改变率(εnow到达给定的下限；

下面来定义误差ε，为了便于比较，误差定义和文献[11]中的定义一致。由于整个算法并未对目标的散射系数进行估计，所以先对散射系数进行估计。式(6)可写为

对所有的L个脉冲有

其中

由式(27)，对散射系数的最小二乘估计为

代入到式(27)，误差ε定义为

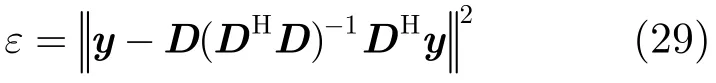
算法步骤 3中更新了目标的收发角和多普勒频率后，即可代入上式计算当前迭代的误差。

5 实验仿真

本节将通过实验仿真和文献[11]的方法进行比较。

参数设置：发射阵元数M=9，接收阵元数脉冲数L=20，脉冲重复周期T=50 μs 。目标数为P=5，目标的收发角和多普勒频率如表1所示。目标散射系数的实部和虚部都从标准正态分布中随机获取。

表1 目标的收发角和多普勒频率

本文算法在 (−90o, 90o)内随机将收发角初始化为在(0,10 kHz)内随机将多普勒频率初始化为fdp0。文献[11]中的初始化采用两种方法：

方法1 同文献[11]中描述的那样采用任选的随机矩阵(本仿真采用标准正态随机矩阵)；

方法2 将本文算法的初值θp0,φp0代入生成A0(φ),B0(θ)，将本文算法的初值fdp0和随机产生的散射系数代入生成C0(fd)。

下面将比较本文算法和采用方法1初始化及方法2初始化的文献[11]算法。

实验1 无噪声时

首先分析最理想的无噪声情况，即式(5)中没有噪声项wn,m,l。给出 1000组实验，每组实验中目标的散射系数和迭代初始值均随机给定。显然这1000组实验都迭代k次时会得到1000个误差，为了查看这1000个误差分布情况，将其绘制成直方图。直方图中横坐标的划分间隔为5，即显示这1000个误差落在[0,5),[5,10),[10,15),…的频数。图2分别显示了迭代10次，20次和30次时，误差分布的直方图。

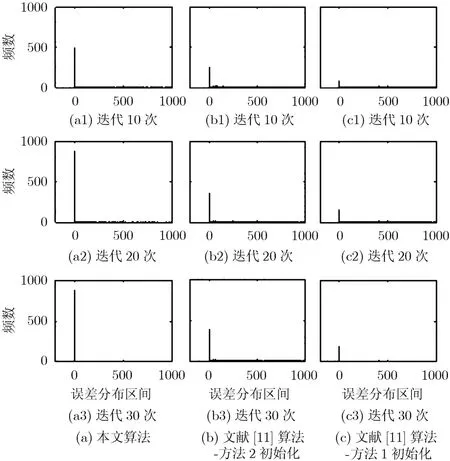
图2 无噪声时的误差分布直方图

由图可见，在迭代10次时，本文算法的误差落在[0,5)的频数约为 500，表明在迭代 10次后 1000次仿真中约一半获得了精度很高的目标收发角和多普勒频率估计，精度较高和精度差的占了另一半。而文献[11]算法落在[0,5)的频数明显小于本文算法，方法1初始化的结果比方法2初始化差。当迭代到20次时，本文算法的误差落在[0,5)的频数约为900，即 1000次仿真中约 90%都获得了精度很高的目标收发角和多普勒频率估计，而文献[11]算法的结果仍明显劣于本文算法，且方法1初始化的结果比方法2初始化差。这是可以理解的，因为方法1的初始化是随机的，而方法2的初始化隐含了矩阵的内在结构特点(即A(φ) ,B(θ),C(fd)行与行之间存在比例关系)，但迭代更新中却没有考虑该结构特点，而本文算法全过程都利用了该结构特点。

当迭代到30次时，所得的结果和迭代20次基本相同，这说明迭代结果已基本稳定，继续迭代到更多次数的结果仍基本相同。为何在无噪声情况下，迭代结果稳定后误差落在[0,5)的频数不是约为1000呢？这是因为本文算法和文献[11]算法对于某些初始值的迭代结果是局部极小点或落在十分“平坦”的面上，所以此时无法获得高精度的目标参数估计。

实验2 噪声方差20.1 σ=时

本实验和实验1的设置一样，只是式(5)中噪声项wn,m,l的方差为0.1。图3分别显示了迭代10次，20次和30次时，误差分布的直方图。

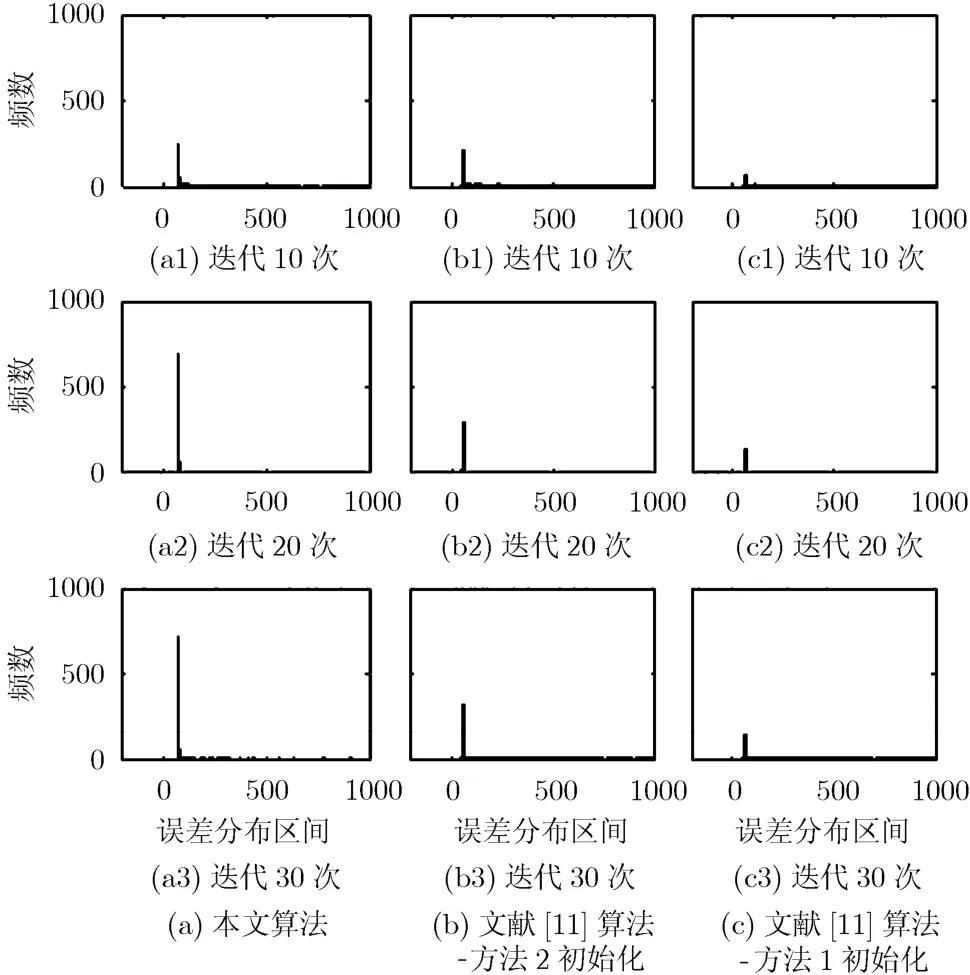
图3 噪声方差20.1 σ=时的误差分布直方图

由图可见，在迭代10次时本文算法和文献[11]算法方法2初始化的结果相当，文献[11]算法方法1初始化的结果很差。在迭代20次和30次时，本文算法的误差主要集中在65至80之间，频数高达900。而文献[11]误差在65至80范围内的频数不到400，误差大于100的频数占了大半。可见，本文算法更易获得高精度估计。

实验3 噪声方差20.2 σ=时

本实验和实验1的设置一样，只是式(5)中噪声项wn,m,l的方差为0.2。图4分别显示了迭代10次，20次和30次时，误差分布的直方图。

图4 噪声方差20.2 σ=时的误差分布直方图

由图可见，在迭代10次时本文算法和文献[11]算法方法2初始化的结果相当，文献[11]算法方法1初始化的结果较差。在迭代20次和30次时，本文算法的误差主要集中在250至300之间，频数约750，误差大于 400的频数约 50。而文献[11]误差在 250至 300范围内的频数不到 350，并且误差大于 400的频数占了大半。再次表明本文算法更易获得高精度估计。

综上所述，相比文献[11]算法而言，本文算法更易获得高精度的目标收发角和多普勒频率估计。另外，由于本文算法每次迭代可并行一步完成，因而减少了运算时间。

6 结论

本文提出了一种新的双基地 MIMO雷达收发角和多普勒频率联合估计方法。利用匹配滤波器输出信号的特点，采用最小二乘法从信号中分别提取出目标的多普勒矢量、接收角矢量和发射角矢量，然后采用迭代算法对这3个矢量进行更新以完成收发角和多普勒频率的联合估计。该方法复杂度低，估计结果能够实现自动配对。与文献[11]基于PARAFAC的方法相比，本文方法更易获得高精度的收发角和多普勒频率估计，且每次迭代可并行一步完成，缩短了运算时间。

[1] Fishler E, Haimovich A, and Blum R S,et al.. Spatial diversity in radars-models and detection performance [J].IEEE Transactions on Signal Processing, 2006, 54(3):823-838.

[2] Li Jian and Stoica P. MIMO radar with colocated antennas[J].IEEE Signal Processing Magazine, 2007, 24(5): 106-114.

[3] Xu L, Li J, and Stoica P. Adaptive techniques for MIMO radar[C]. Proceedings of Sensor Array and Multi-channel Signal Processing, IEEE Workshop, Waltham, MA, 2006:258-262.

[4] Chen Jin-li, Gu Hong and Su Wei-min. Angle estimation using ESPRIT without pairing in MIMO radar[J].Electronics Letters, 2008, 44(24): 1422-1423.

[5] Liu N, Zhang L R, Zhang J,et al.. Direction finding of MIMO radar through ESPRIT and Kalman filter[J].Electronics Letters, 2009, 45(17): 908-909.

[6] Bencheikh M L and Wang Y. Joint DOD-DOA estimation using combined ESPRIT-MUSIC approach in MIMO radar[J].Electronics Letters, 2010, 46(15): 1081-1083.

[7] Zhang X and Xu D. Angle estimation in MIMO radar using reduced-dimension Capon[J].ElectronicsLetters, 2010,46(12): 860-861.

[8] 陈金立, 顾红, 苏为民. 一种双基地 MIMO 雷达快速多目标定位方法[J]. 电子与信息学报, 2009, 31(7): 1664-1668.Chen Jin-li, Gu Hong, and Su Wei-min. A method for fast multi-target localization in bistatic MIMO radar system[J].Journal of Electronics&Information Technology, 2009, 31(7):1664-1668.

[9] 谢荣, 刘峥. 基于多项式求根的双基地 MIMO 雷达多目标定位方法[J]. 电子与信息学报, 2010, 32(9): 2197-2220.Xie Rong and Liu Zheng. Multi-target localization based on polynomial rooting for bistatic MIMO radar[J].Journal of Electronics&Information Technology, 2010, 32(9):2197-2220.

[10] 吕晖, 冯大政, 和洁, 等. 一种新的双基地MIMO雷达目标定位和多普勒频率估计方法[J]. 电子与信息学报, 2010, 32(9):2167-2171.Lü Hui, Feng Da-zheng, He Jie,et al.. A novel method for target localization and Doppler frequency estimation in bistatic MIMO radar[J].Journal of Electronics&Information Technology, 2010, 32(9): 2167-2171.

[11] 张剑云, 郑志东, 李小波. 双基地 MIMO 雷达收发角及多普勒频率的联合估计算法[J]. 电子与信息学报, 2010, 32(8):1843-1848.Zhang Jian-yun, Zheng Zhi-dong, and Li Xiao-bo. An algorithm for DOD-DOA and Doppler frequency jointly estimating of bistatic MIMO radar[J].Journal of Electronics&Information Technology, 2010, 32(8): 1843-1848.