一种基于特征提取的车载前视步进频率虚拟孔径雷达速度补偿方法

王鹏宇 周智敏 金 添 王玉明

(国防科技大学电子科学与工程学院 长沙 410073)

1 引言

车载前视步进频率探地雷达通过发射瞬时窄带的步进频率信号合成大的信号带宽，能够穿透地表对地雷等浅埋目标进行有效探测，系统采用分裂孔径发射配置(Split Aperture Transmit Configuration,STAC)[1,2]，在同样孔径长度下可以实现与传统单站SAR相当的方位分辨率。国防科学技术大学 2007年研制的车载超宽带步进频率前视虚拟孔径探地雷达演示系统(SFGPVAR)是典型的虚拟孔径阵列超宽带雷达。

SFGPVAR系统采用 4发-16收的分裂孔径配置，接收天线孔径长3.2 m，发射天线位于天线阵两端(左右各 2个)，但考虑系统可靠性与实时性的要求，系统采取收发模块复用结构设计，即两个发射天线复用一个发射机，4个接收天线复用一个接收机，与单站SAR工作方式相比，SFGPVAR系统的多发射单元通过分时工作并以电扫描方式实现虚拟孔径的合成。由于步进频率信号是速度敏感信号，运动速度会造成目标1维距离像的展宽和平移[3]，而SFGPVAR系统为满足大范围区域的较高探测率要求通常工作在低速模式，此时1维距离像的展宽和平移均小于半个距离分辨单元，因此可以忽略速度对1维成像的影响。但是系统的收发模块复用设计在增加系统稳定性的同时也增长了孔径合成时间，在2维成像过程中使得目标能量不能有效累积，造成散焦甚至分裂，严重影响目标特征提取及其检测鉴别。

由于步进频率信号速度的敏感性，使得运动补偿一直是步进频率雷达信息处理的研究重点，现有研究也大都集中于动目标的运动参数估计问题，虽然通过改变信号重复频率[4]、信号发射机制[5]等方法能够实现目标径向速度的精确估计和1维高分辨成像，却往往忽略速度对2维成像的影响，文献[6]利用传感器数据仅对车辆运动造成的天线姿态误差造成的图像几何畸变进行了有效补偿，但没有详细分析测量误差、更新速率等因素对补偿效果的影响，因而缺乏切实有效的运动补偿方法。本文以SFGPVAR系统为基础，通过建立点目标回波模型分析了径向速度、垂直向速度对成像的影响，给出了速度补偿等效原理，提出基于 ROI(Range Of Interest)图像紧致度最优的速度补偿方法并给出了相应的信息处理流程，新方法提高了补偿效率，在增强目标特征一致性的同时提高了目标检测率，仿真和实测数据均验证了新方法的有效性。

2 运动速度对2维成像的影响

根据SFGPVAR系统建立如图1所示的简化点目标回波模型，建立直角坐标系。

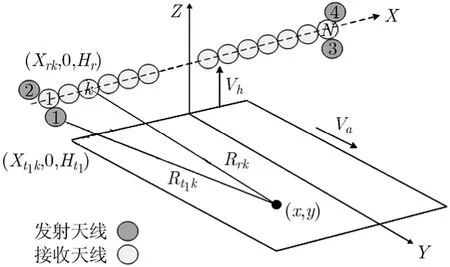
图1 SFGPVAR系统简化点目标回波模型

目标地面坐标(x,y)，发射天线1发射信号，第k个接收天线(Xrk,0,H)接收回波为[7]

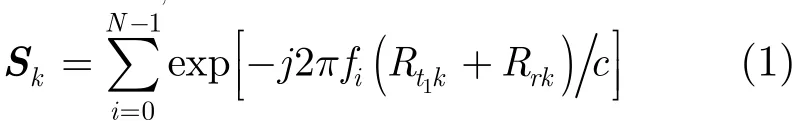
其中c为电磁波在真空中的传播速度，发射信号频率fi=f0+i·Δf,f0为发射信号起始频率，i为发射信号序号，Δf为频率步进增量，N为频点总数，Rrk与Rt1k分别为收发天线与点目标之间的距离，Ht1为发射天线1高度，Hr为接收天线高度，且Ht1≈Hr=H。设径向速度和垂直向速度分别为Va、Vh，脉冲重复周期为Tr，则Rt1k、Rrk可表示为

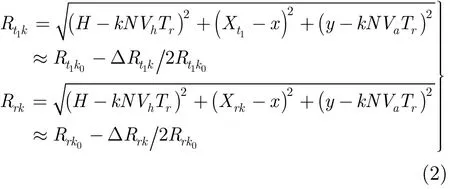
其中

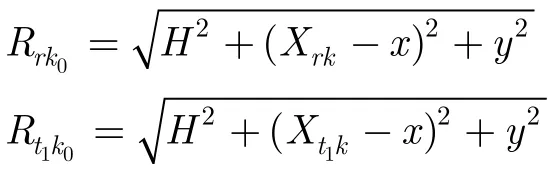
分别为车辆静止时收、发天线与目标间距离。由车辆运动速度造成的距离误差 ΔRt1k,ΔRrk为

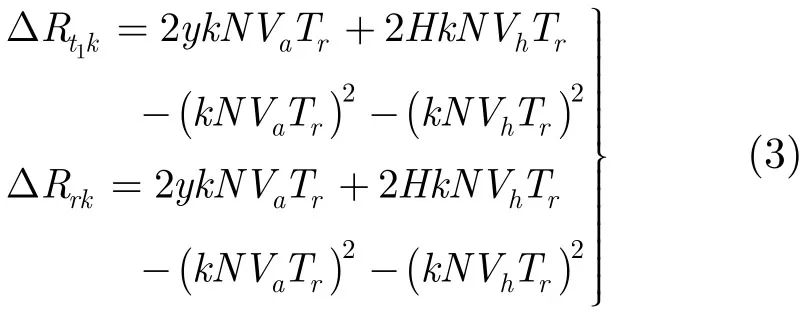
将式(2)代入式(1)，做IFFT处理得到目标复数1维距离像Hk(l)：

相位项P(k)具体表达式为

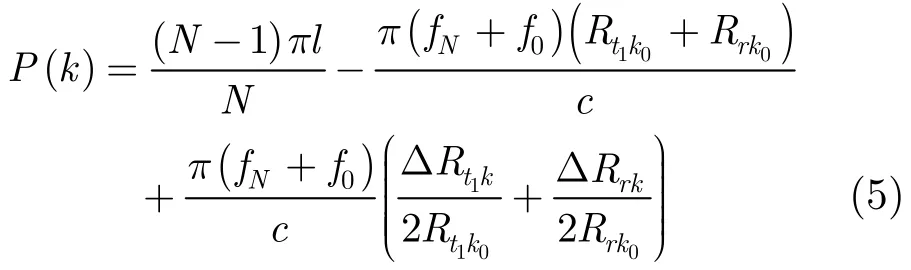
式(5)的第1项是常数，只与目标位置相关，不会影响方位聚焦；目标信息包含在第2项中，该项也只与目标位置相关；第3项是由径向速度与垂直向速度引入的相位误差，具有空变性，影响目标能量方位向相干累积，造成分裂甚至散焦，下面通过仿真进一步说明。SFGPVAR系统发射 Δf=2 MHz 的步进频率连续波，脉冲重复周期Tr=2 μs，系统有效带宽B=1.8 GHz ，点目标地面坐标(0,8)。

从图2，图3结果可知：运动速度使目标方位能量不能有效累积，造成目标散焦甚至分裂，分裂目标基本以目标真实位置为中心左右对称，对比图3(b), 3(c)可知，在相同速度条件下径向速度较垂直向速度对成像的影响更为严重。

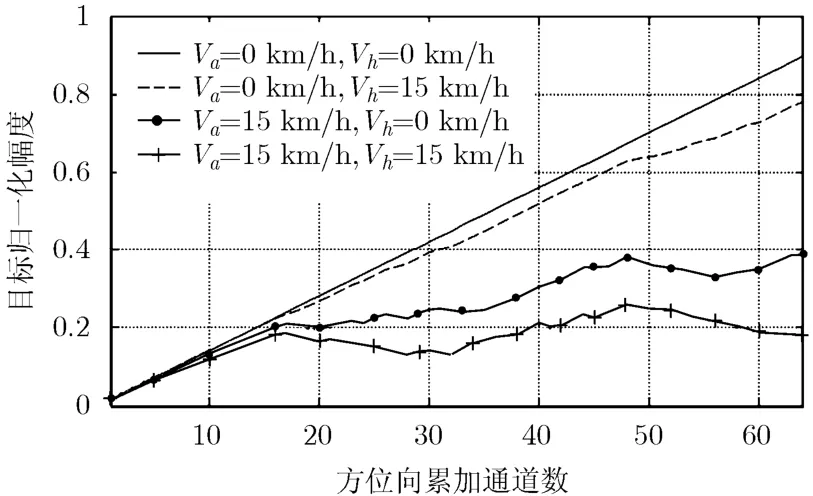
图2 点目标方位能量积累曲线

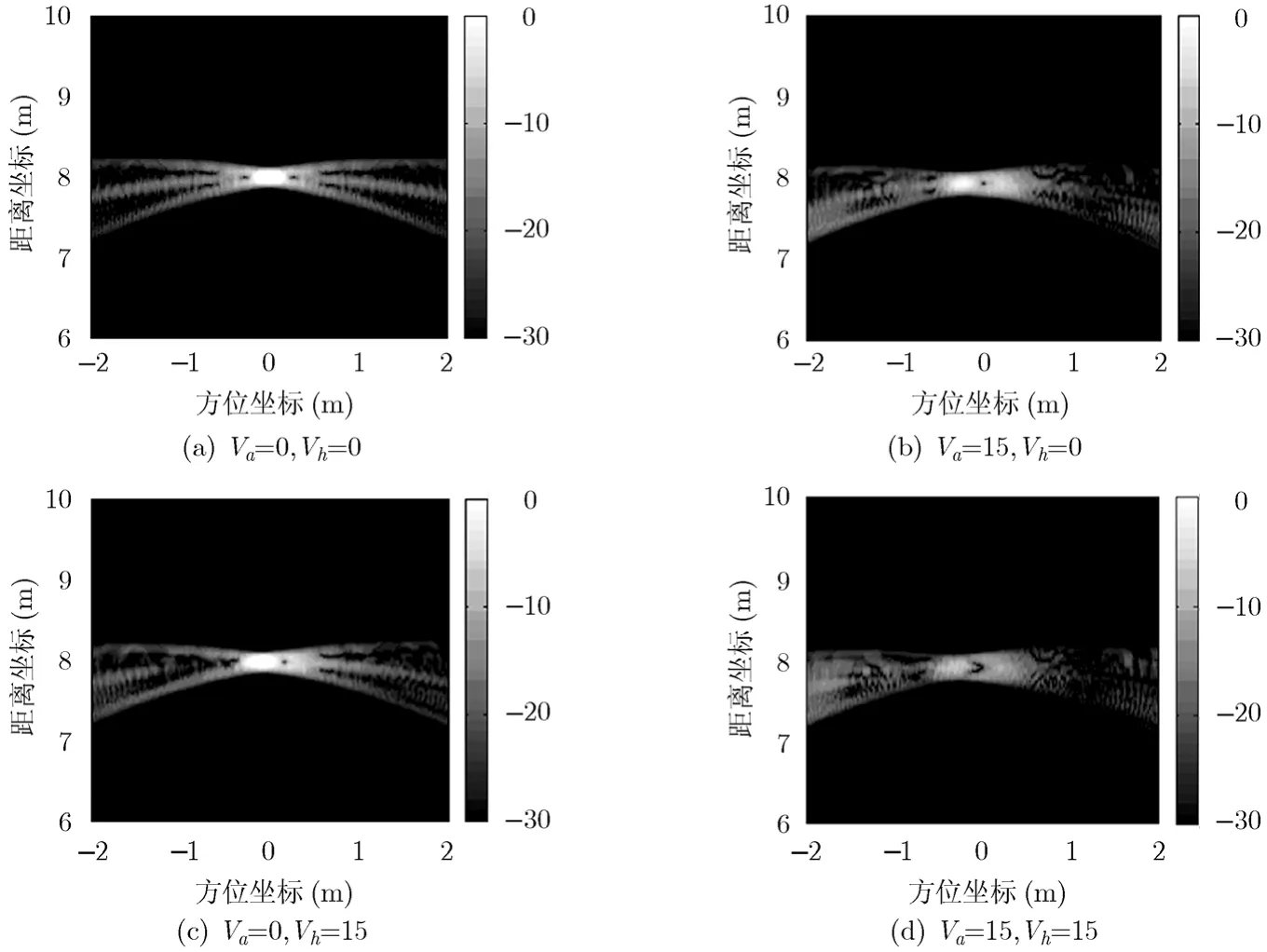
图3 不同速度条件下的点目标2维图像

3 基于ROI图像紧致度最优速度补偿方法

SFGPVAR系统通过分裂发射孔径配置实现了方位分辨的提高，但运动速度造成目标分裂甚至散焦，严重影响目标特征提取的稳健性。本节在前文分析的基础上，根据点目标回波模型推导出速度补偿等效原理，并在此基础上提出基于ROI图像紧致度的最优速度补偿方法并给出了相应的信息处理流程。

3.1 速度补偿等效原理

定义速度误差相位Perr(k)为

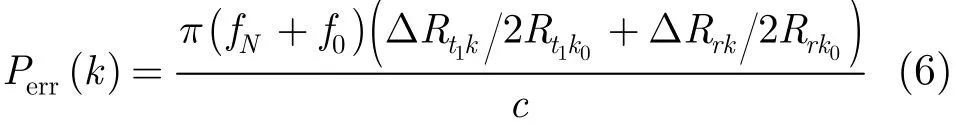
将式(3)代入式(6)化简得

PerrVa(k)与PerrVh(k)分别为径向速度与垂直向速度引入的相位误差：

由式(8)可知：PerrVa(k)只是径向速度Va的一元函数，PerrVh(k)而只是垂直向速度Vh的一元函数，两者均不存在速度耦合误差，即PerrVa与PerrVh相互独立，因此可以对速度误差分别补偿。需要指出的是：径向速度通常由车速传感器获得，但受到测量精度限制，测量值与实际值之间总存在一定偏差，尤其是车辆在加减速时测量偏差更大；垂直向速度通常由加速度计获得，但受测量精度限制，加速度计很难对车辆颠簸产生的垂直向速度进行及时准确的测量，那么SFGPVAR系统运动补偿实质可认为是具有一定先验信息的寻求2维最优解问题，但无论是计算量还是计算复杂度都很难满足系统实时性的要求，基于以上分析，降低求解维数是较为理想的解决方式。

由于SFGPVAR系统通常工作于低速模式，因此可以忽略式(8)中速度的2次项，则相位误差化简为速度的1次函数，当目标位置已知时，PerrVh可化为

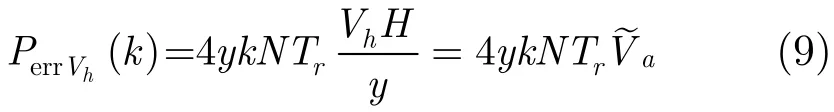
其中可视为垂直向速度Vh的径向投影，投影系数为VhH/y，且只与目标径向位置y相关，因此等效径向速度具有空变性。将式(9)代入式(7)得

基于以上分析可知：垂直向速度Vh可近似等效为径向速度，这使运动补偿2维速度的最优求解简化为1维径向速度的最优求解，由于车速传感器能够提供较为准确的径向速度测量值，因此该1维最优求解也进一步变为具有先验信息的最优化问题。

3.2 紧致度最优速度估计

其中Einner是目标ROI图像中目标切片能量，Eouter为目标切片之外的图像残余能量。紧致度越大，能量越集中，目标聚焦越好，紧致度实质是ROI图像对比度。图4为图3(b)仿真点目标归一化的紧致度-速度补偿曲线，紧致度最大时对应的速度值即为车辆运动速度，因此紧致度适用于衡量速度补偿效果的优劣，由于最优化算法不是本文研究的重点，故在此不做深入讨论。

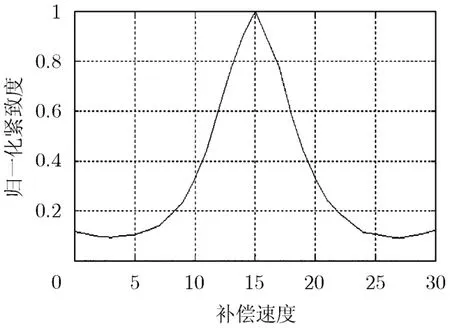
图4 紧致度-速度补偿曲线

在SFGPVAR系统工作过程中，垂直向速度Vh与径向速度Va均为未知定值，车速传感器只能提供Va的粗略测量值，存在测量误差ΔVa，根据式(9)，式(10)，联立不同目标ROI的速度估计方程即可求解Va,Vh：

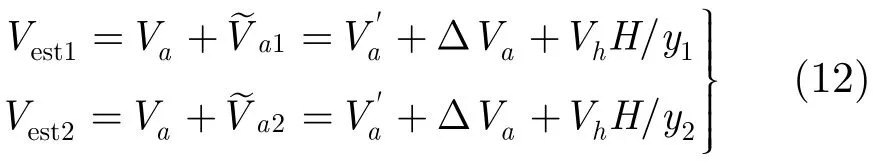
基于紧致度的速度补偿是以速度粗补偿的ROI图像为基础，图像信杂比是影响速度估计的重要因素，由于SFGPVAR系统实际工作环境复杂多变，因此需要对ROI图像做以下预处理：

(1)ROI图像排序：基于速度粗补偿成像的检测结果提取ROI，根据信杂比大小对ROI图像排序并记录目标位置信息，然后筛选一定比例ROI图像进行速度；

(2)聚焦中心估计：根据图3仿真结果可知，运动速度造成目标左右分裂，影响检测对目标位置信息的获取，因此有必要对粗补偿ROI图像的聚焦中心进行重新估计，基于目标分裂形式，本文选取重心作为聚焦中心。图5为图3(b)仿真点目标聚焦中心估计前后速度补偿效果对比，可以看出：由于聚焦中心偏差，目标偏离真实位置并存在明显旁瓣。

图5 聚焦中心估计前后速度补偿结果对比

根据以上分析，如图6给出了基于紧致度最优速度补偿的信息处理流程。

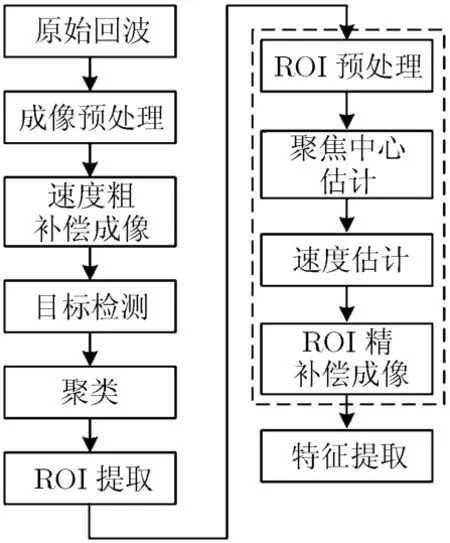
图6 紧致度最优速度补偿信息处理流程

4 实测数据处理结果

SFGPVAR系统主要用于探测金属防坦克地雷，系统有效探测宽度6 m，探测距离5-21 m，系统是通过提取目标图像特征实现地雷的检测鉴别，因此地雷特征提取的一致性是影响检测鉴别的重要因素。根据文献[9-11]本文选择了地雷具有代表性的6个特征，与杂波区分性较强，适用于地雷目标鉴别。图7(a)-7(d)为系统实测金属埋地地雷不同速度补偿的成像结果，可以看出：图7(a)由于没有进行速度补偿，目标分裂出较大旁瓣；图7(b)利用车速传感器数据进行粗补偿成像，目标得到有效聚焦，但仍然存在分裂旁瓣；图7(c)直接利用检测所得目标位置信息进行速度补偿成像，较图7(b)有一定改善；图7(d)在对聚焦中心重新估计的基础上实现了目标良好聚焦，消除了分裂旁瓣。

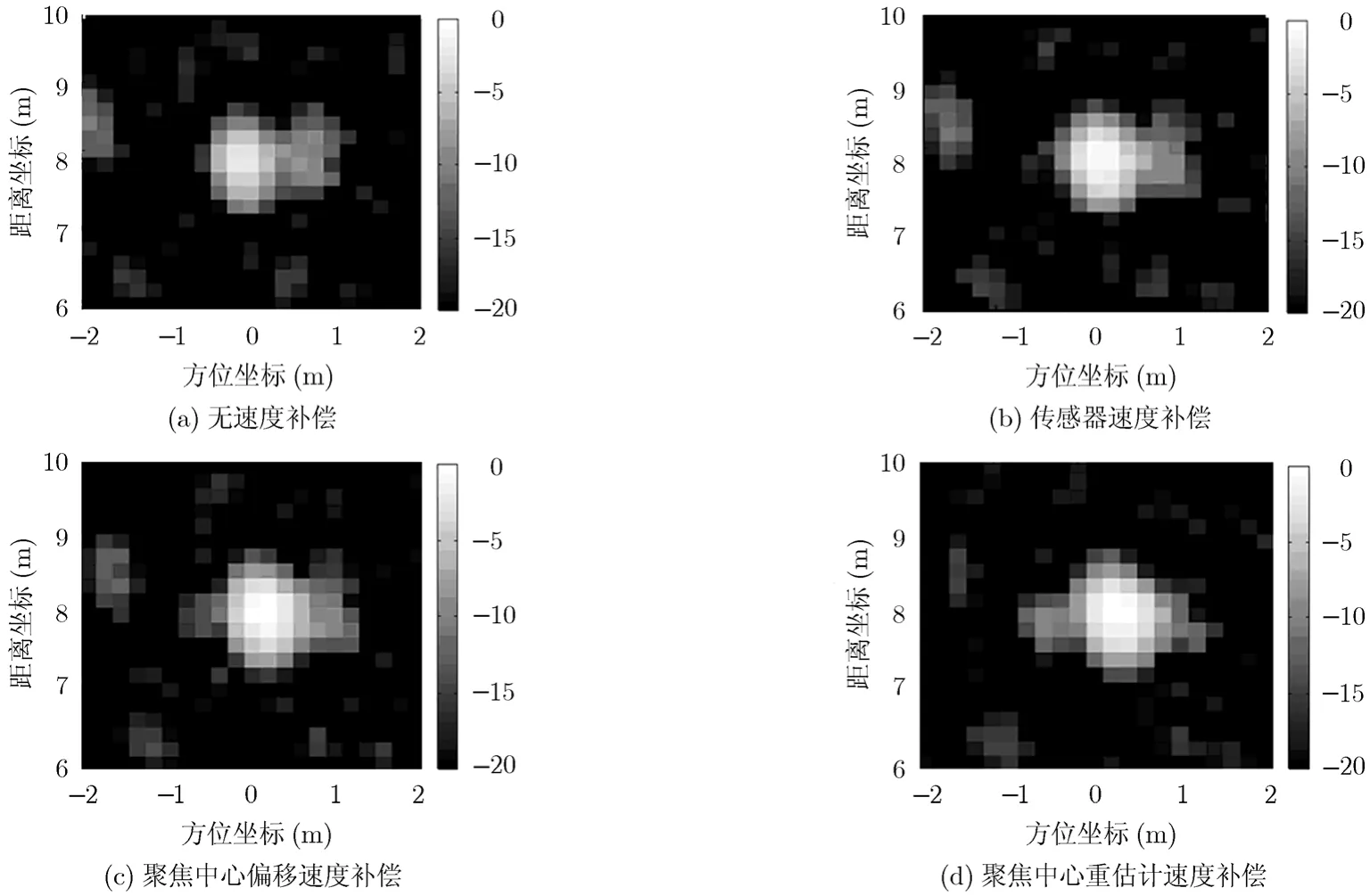
图7 实测地雷不同速度补偿结果

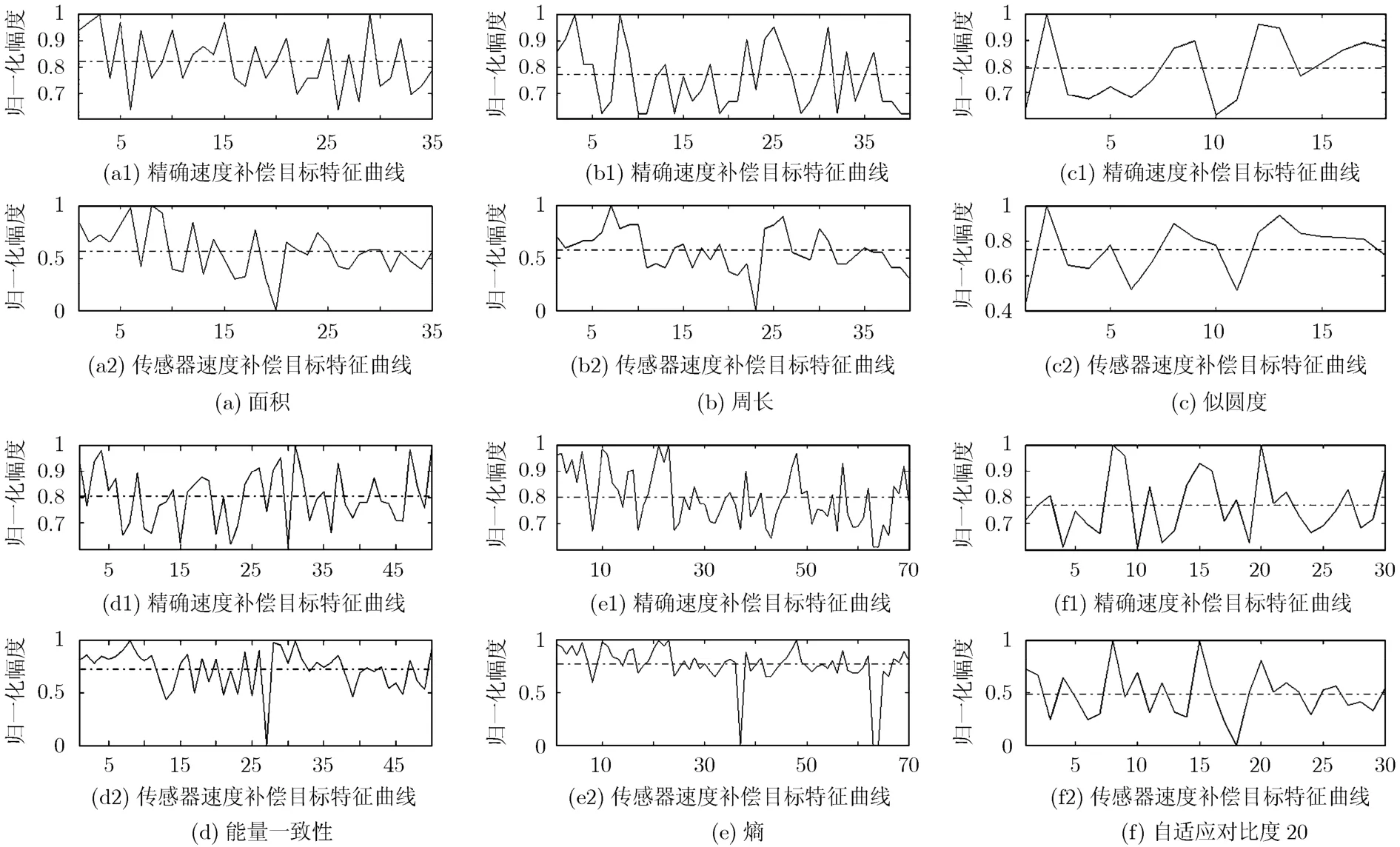
图8 地雷ROI图像特征值曲线

由于系统采用分裂孔径发射配置，目标特征具有空变特性，图8(a)-8(f)为 SFGPVAR系统车前8-16 m内目标速度补偿前后特征值对比曲线，其中实线为特征值曲线，虚线为对应的均值曲线，横坐标为目标ROI序号，纵坐标为目标对应的归一化特征值。从结果可以看出：经过精确速度补偿后的目标特征值波动幅度较小，且不存在较为明显的幅度奇点，特征值方差对比如表1所示。图9为SFGPVAR系统行进探测试验中对金属地雷的检测率曲线，对比可见，基于紧致度最优速度补偿提高了目标特征提取的稳定性，更有利于目标的检测鉴别。

表1 不同速度补偿方法目标特征方差对比表

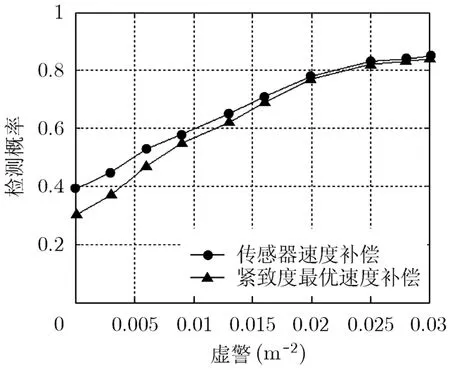
图9 不同速度补偿方法检测率对比曲线

5 结论

车载前视步进频率虚拟孔径雷达受运动速度影响会造成目标图像散焦甚至分裂，严重影响目标图像特征提取的一致性。本文通过建立点目标回波模型，分析车辆径向速度、垂直向速度对成像影响，通过模型近似给出了速度补偿等效原理，在此基础上提出了基于目标ROI图像紧致度最优的速度补偿方法，有效改善了补偿效果，增强了目标特征一致性，结合实际对SFGPVAR系统信息处理流程进行了相应改进，仿真和实测数据处理结果验证了该方法的有效性。

[1] Jin Tian and Zhou Zhi-min. Imaging model of forwardlooking ground penetrating radar with split-aperture transmitting configuration. 2nd Asian and Pacific Conference on Synthetic Aperture Radar, Xi’an, China, 2009: 21-24.

[2] Jin Tian, Song Qian, and Lu Bi-ying. Virtual array imaging radar azimuth resolution analysis. IET International Radar Conference, Guilin, China, 2009: 223-226.

[3] Chen Juan, Zeng Tao, and Long Teng. A novel high- resolution stepped-frequency SAR signal processing method. IET International Radar Conference, Guilin, China, 2009: 1-4.

[4] 胡光, 曾大治, 龙腾. 基于变PRT步进频率信号对运动目标同时测距和测速点方法研究. 信号处理, 2010, 26(11):1627-1631.

[5] Liu Lin, Tian Jin-jun, and Lin Zhan-hui. A parameter estimation method for moving target in stepped frequency radar.ICICTA 2010, Changsha, China, 2010, Vol.1: 289-292.

[6] 杨延光, 周智敏, 宋千. 基于SATC-CABP成像模型的天线姿态误差补偿方法. 系统工程与电子技术, 2008, 30(10):1819-1823.

[7] Dang Hong-xing. Stepped frequency chirp signal SAR imaging. 2007 APSAR, Huangshan, Chian, Nov. 2007: 14-18.[8] Paul Gader. Detecting landmines with ground-penetrating radar using feature-based rules, order statistics, and adaptive whitening.IEEE Transactions on Geosciences and Remote Sensing, 2004, 42(11): 2522-2534.

[9] 郭雷. 宽带雷达目标极化特征提取与核方法识别研究. [博士论文], 国防科技技术大学, 2009.

[10] Carin L, Geng N, McClure M,et al.. Wide-area Detection of Land Mines and Unexploded Ordnance. London: UK, Institute of Physics Publishing Ltd, 2002: 575-609.

[11] Naga R, Mudigonda R K, and Palmer D. Detection and classification of land mine targets in ground penetrating radar images. Proceedings of SPIE, 2002, Vol. 4742: 390-400.