近距离大转角目标超宽带ISAR成像

徐艳云 张群英 方广有

①(中国科学院电子学研究所 北京 100190)

②(中国科学院研究生院 北京 100190)

1 引言

在微波成像技术中，合成孔径雷达(SAR)和逆合成孔径雷达(ISAR)是两个重要应用，两者均利用雷达与目标的相对运动进行成像[1]。传统的SAR或ISAR成像中，为了解决信号带宽和作用距离之间的矛盾，发射信号一般为线性调频或步进频信号。而对近距离目标，直接利用超宽带时域测量即可达到高分辨，超宽带雷达正是由于其高分辨率以及较强的穿透能力，近年来得到广泛的应用，如国内外对穿墙、探地雷达的应用研究[2−5]，对医学成像、生命检测及目标识别等方面的应用研究[6−8]。如何将微波成像技术更好地应用于各领域有着广阔的前景和巨大的挑战，因此对近距离目标高分辨微波成像的研究有重要的意义。

本文第2节分析成像系统几何和成像原理；第3节考虑易于补偿散射点越分辨单元走动(Migration Through Resolution Cell, MTRC)[9]的滤波球后向投影，并从几何上说明滤波用于补偿转动角度离散化带来的数据误差[10]的作用，针对接收回波中的噪声污染等问题，提出具有强鲁棒性的频域加窗滤波球后向投影(Windowing Filtered Spherical Back Projection, WFSBP)算法实现目标的高分辨成像，并分析了成像点扩散情况及单频发射时的目标成像；第4节通过仿真和实测数据验证理论的正确性和算法的优越性；第5节为结束语。

2 旋转成像几何

转动目标成像几何如图1所示，雷达静止，目标随转台以O为轴心逆时针转动，用两个坐标轴描述旋转目标，x-y为旋转坐标轴，u-v为固定坐标轴。雷达视线方向为距离向，在转台旋转平面内与雷达视线正交的方向为方位向，距离-方位平面为成像投影平面。

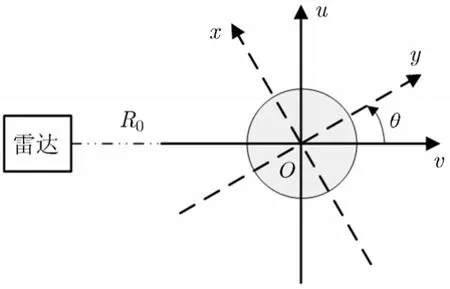
图1 转台成像模型

旋转坐标轴x-y与固定坐标轴u-v的关系如下式所示：

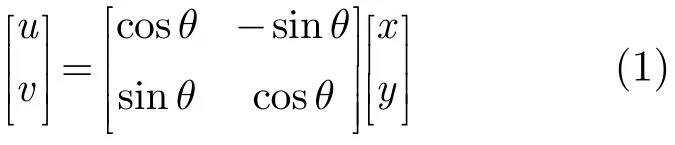
θ为目标旋转角度。雷达和目标散射点之间的距离为

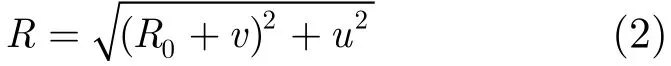
R0表示雷达与转台中心O的距离，为一固定值。设目标始终处于雷达波束内，无多次散射，若发射信号为st(t),f(x,y)表示目标函数，则接收回波信号为

从式(1)-式(3)可知回波信号是快时间域t和慢时间域θ的函数。成像借助于目标的转动产生方位向上的分辨，旋转角度为小角度(3o-5o)时也可实现成像[1,11]，但小角度相干积累时间短，分辨率差。高的方位分辨率的获得，需要较大的合成孔径，即目标转动大的角度，对大转角目标即使发射单频信号也可获得高分辨图像[12,13]，而大转角会带来散射点的MTRC，利用适当的算法可实现目标准确高分辨成像。

3 成像算法及点扩散函数分析

3.1 算法原理

时域后向投影算法对目标转角没有苛刻的限制，广泛应用于超宽带大合成孔径成像中[14,15]，能补偿大转角目标散射点MTRC。对于转动目标，在平面波近似下，根据投影切片定理即接收信号在角度θ上的傅里叶变换等于目标函数空间 2维傅里叶变换在角度θ上的投影，易得到滤波后向投影(Filtered Back Projection, FBP)算法[16]，目标转动一周可获得最好的成像效果。当发射信号为冲激信号时，滤波后向投影成像公式为

式中f为频率，k=2πf/c为波数，Sr(f,θ)为式(3)所示sr(t,θ)的快时间傅里叶变换，均为极坐标数据格式，如图2和图3所示。从几何角度分析，由图2可以看出只在角度间隔为 Δθ= 2π/N的离散角度上获取N次目标回波，而在其他角度上没有数据，当N足够大时可减少数据误差，但同时增加了数据量，因此在给定N条件下，需对该误差进行补偿以实现更精确成像。式(4)通过对回波信号的理想滤波，对每次采样回波频域加权，权值即为弧长lw=kΔθ，如图3所示。越远离圆点其权值越大，符合极坐标格式特点，从而补偿了转角离散化带来的数据误差。

图2 时域极坐标数据

图3 频域极坐标数据及加权补偿

考虑电磁波传播的球面特性，由式(2)计算雷达到目标的距离，后向投影累加曲线沿弧线进行(球后向投影)，式(4)即为滤波球后向投影(FSBP)公式。当有噪声存在时，由式(4)对回波的理想滤波，在补偿转角离散化带来的数据误差的同时，却增强了高频噪声，从而影响成像质量，通过频域加窗降低高频噪声的影响，即WFSBP成像公式为

频域加窗将增大成像主瓣宽度，降低成像分辨率，本文W(k)为可调节频域Kaiser窗函数，可根据第1类修正零阶贝赛尔函数近似得到[17]：

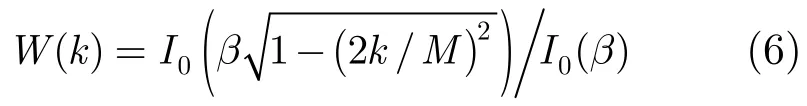
其中M是窗函数长度，为第1类修正零阶贝赛尔函数，β是可调参数，可调节主瓣宽度和旁瓣电平的衰减比例，β越大旁瓣越小，主瓣宽度则相应增加，从而影响成像分辨率，图4所示为所使用的理想滤波器，β=10的频域Kaiser窗函数以及加窗滤波器的频域图，第4节将对该算法进行仿真和实测验证。

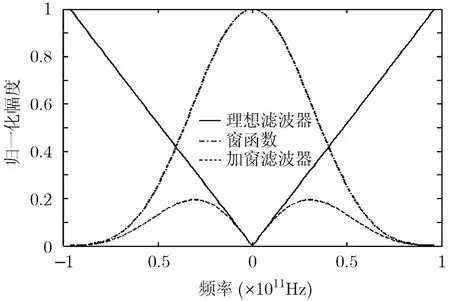
图4 频域窗函数及滤波器函数

3.2 点扩散函数

设波数k在kmin和kmax范围内，目标位置为r=(x,y)，为分析简单，目标转动360o，则式(4)可写为

对于中心理想点目标f0(r)=δ(r)，并根据式(3)得到目标回波数据后，由式(7)计算得成像点扩散函数[12]为

J0(·)和J1(·)分别为零阶和一阶贝赛尔函数。当k为常数时，可得可见即使发射信号为单频信号，对于大转角目标仍可获得高分辨图像。

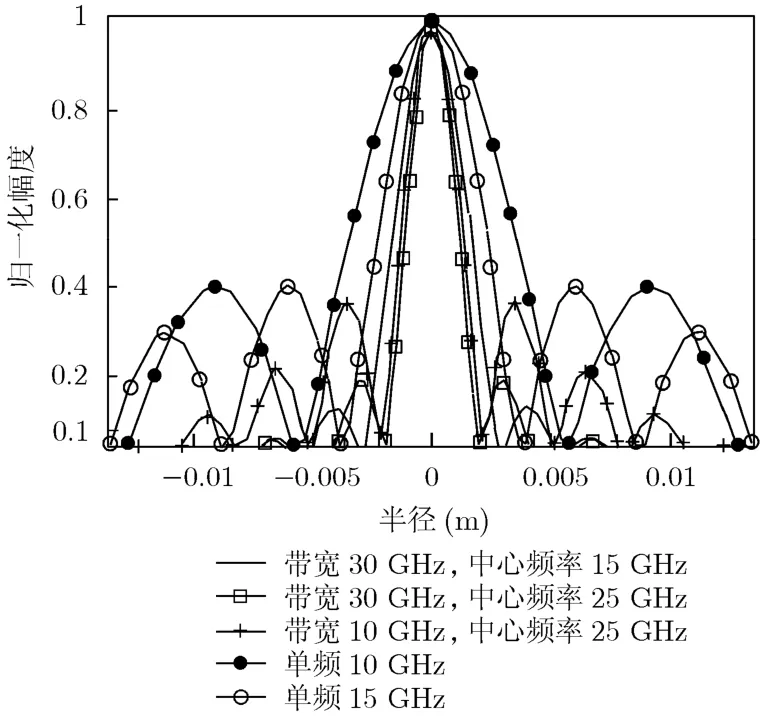
图5 点扩散函数

设图像区域长宽均为 4 cm，网格划分间隔为0.05 mm，根据式(8)得到点扩散函数如图5所示，实线kmax=30 GHz,kmin=0 GHz(带宽30 GHz，中心频率 15 GHz)，虚线kmax=40 GHz,kmin=10 GHz(带宽30 GHz，中心频率25 GHz)，半幅度宽度分别为 3.4 mm和 2.4 mm，峰值旁瓣比分别为-17.56 dB和-14.19 dB，可见相同带宽下，中心频率越高分辨率越高；由*标记线kmax=30 GHz,kmin=20 GHz(带宽10 GHz，中心频率25 GHz)，其半幅度宽度为2.27 mm，峰值旁瓣比为-8.72 dB，可见带宽不再是决定分辨率的主要因素；由·标记线和○标记线为发射10 GHz和15 GHz单频信号时的点扩散函数，半幅度宽度分别为 7.1 mm 和 4.7 mm，可见频率越高分辨率越高，较之宽带发射信号，单频发射时的旁瓣电平较高，其峰值旁瓣比约为-8 dB。第4节将进行目标的成像仿真分析。

4 仿真与实测分析

4.1 超宽带发射信号成像仿真

通过理想点目标成像仿真，对算法进行比较验证，发射信号为峰值的-6 dB脉宽为30 ps的高斯窄脉冲，设雷达到转台中心的距离为4 m，目标区域最大长度和宽度均为4 cm，总旋转角度为2π，点目标位于(1 cm, 1 cm)处。

(1)无噪声存在时 为了提高回波后向投影的精度，对回波线性插值后成像处理，首先比较传统的后向投影(SBP)算法和使用理想滤波的 FSBP算法，成像结果分别如图6(a)和6(b)所示，从图6(a)可见点目标之外为非相干累加点，其能量随着离目标的距离呈高斯变化，点扩散严重，随转动角度扫过一周，形成高斯“脊”；从图6(b)可见对回波信号进行理想滤波后，点目标扩散减小。定量分析点目标距离和方位向切片如图7所示，取峰值的-6 dB脉宽列于表1，可见滤波补偿了转动角度离散化带来的数据误差，提高了成像分辨率。

表1 算法分辨率(mm)

图6 算法比较

图7 切片分析

对回波的插值精度影响后向投影的精度，从而会影响成像质量，以上均是对回波做线性插值，如果采用更精确的sinc插值，两种算法的分辨率如表2所示，与表1比较稍有提高，但差别较小，因此本文使用线性插值已足够得到高质量的图像。

表2 sinc插值分辨率(mm)

(2)有噪声存在时 由以上分析可知，FSBP成像分辨率最高，若在回波中加入信噪比为-15 dB的高斯噪声，比较使用理想滤波器FSBP算法和频域加窗滤波器的WFSBP算法，成像结果分别如图8(a)和 8(b)所示。由两图可知，在低信噪比条件下，对大转角目标仍可实现高分辨率成像，比较两图可知，频域加窗WFSBP算法能有效的降低高频噪声的影响，成像质量更好。

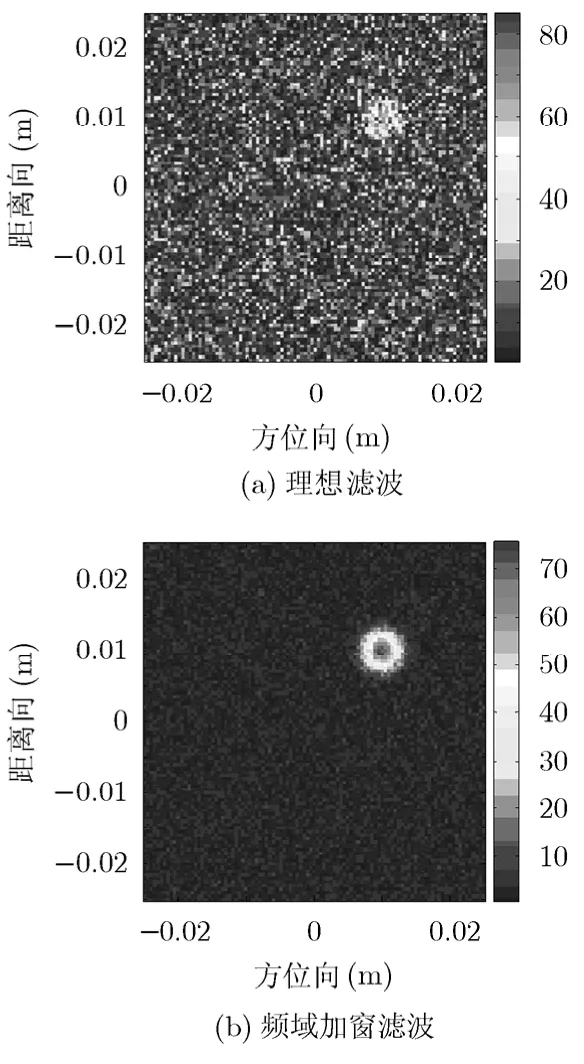
图8 成像结果

如同图7分析距离和方位向切片，分析频域加窗WFSBP成像结果图的距离和方位分辨率分别为4.7 mm和5.1 mm。可见，频域加窗滤波球后向投影算法(WFSBP)具有较好的稳定性，在有噪声存在的情况下，能获得更高质量的目标图像，但是以牺牲分辨率为代价。

4.2 单频发射信号的成像仿真

由第 3节分析点扩散函数可知发射单频信号时，对大转角目标也可实现高分辨成像。对位于(1 cm, 1 cm)处的点目标旋转 360o仿真成像结果如图9(a)和9(b)所示，图9(a)为发射频率为15 GHz的成像图，如同以上分析目标的距离和方位向切片，得分辨率为4.8 mm，峰值旁瓣比约为-7.90 dB，图9(b)为发射频率为10 GHz的成像图，同理分析距离和方位向切片，其分辨率为7.2 mm，峰值旁瓣比约为-7.89 dB。

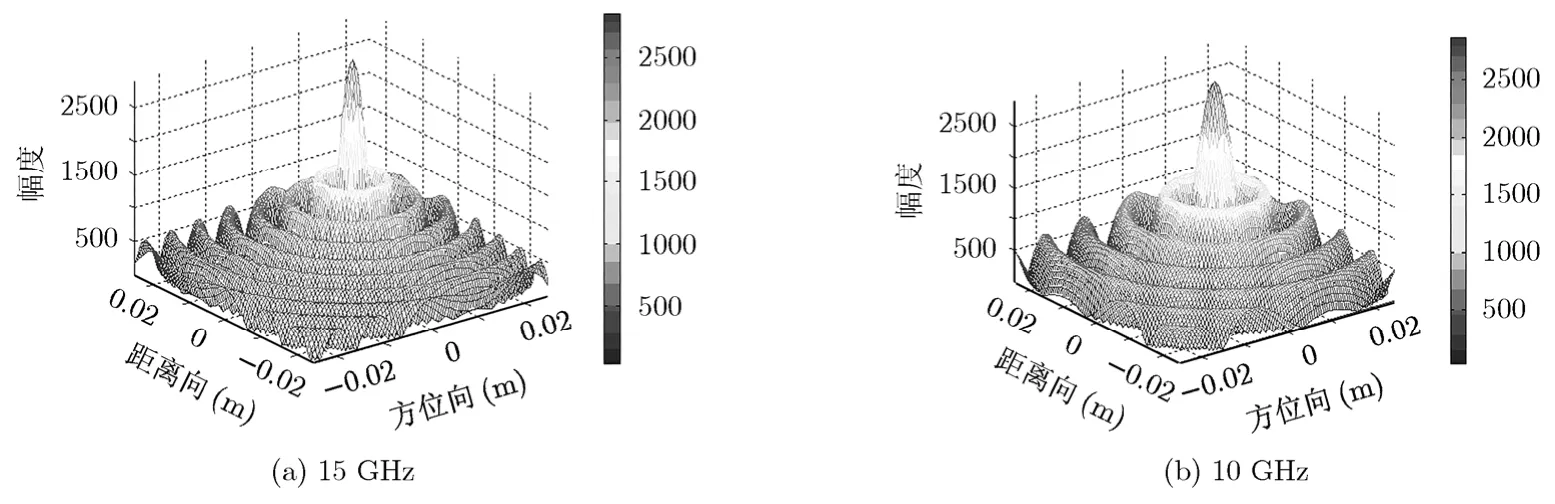
图9 单频成像结果

由以上分析可以看到，对于大角度转动目标，即使是单频发射信号，也可得到高分辨率的图像，且频率越高分辨率越高，但相比超宽带发射信号，单频发射的成像旁瓣较高，容易淹没周围弱目标，因此实际中采用超宽带发射信号获得高距离分辨率的同时，降低旁瓣电平，提高目标探测及成像精度。

4.3 实测分析

图10 实验测量系统

通过搭建超宽带时域ISAR转台成像实验系统获取实测数据(如图10)，两天线构成准单站系统，天线带宽1-18 GHz，驻波比＜1.5，天线到转台中心的距离为 3 m，转台转角精度为±0.02o，图中实心箭头表示触发或控制信号，空心箭头表示数据传输。由触发脉冲为脉冲发生器主机提供外触发，脉冲发生器主机产生的脉冲信号分别提供触发给脉冲发生器头和取样示波器，从而实现发射与接收的同步。

脉冲发生器头产生脉宽为30 ps的窄脉冲信号，窄脉冲信号由发射天线辐射出去，经目标后向散射后到达接收天线，由高性能的Wave expert 100H取样示波器以等效250 GHz的取样率接收回波，以计算机为控制中心，利用自行研发的数据采集软件实现转台转动和数据采集的自动化，转台每转动1o存储一次回波数据，直到目标旋转360o获取各个方向的目标信息。在接收数据过程中转台处于动态，转台转动速度远小于电磁波传播速度，在发射和接收时认为转台静止。为了准确存储目标回波信息，根据目标大小和转速，本实验脉冲重复频率(PRF)满足式(9)，保证目标回波在一个周期内全部被接收到，且脉冲重复周期(1/PRF)远小于转台转动1o的时间，保证每度存储的回波数据为目标在该角度时的后向散射数据。

其中ω为转动角速度，Rmax和Rmin分别为目标到天线的最远和最近距离。本实验目标区域小于50 cm，转台转速0.0524 rad/s，脉冲重复频率PRF为600 kHz，满足式(9)条件，通过对回波延时的精确校正，并针对采样时间窗内的杂波干扰，使用成像算法与背景对消技术相结合实现近距离目标的成像。

将底部直径为5 cm的小圆锥体放置转台左侧，距离转台中心 10 cm，传统的球后向投影(SBP)算法、理想滤波的 FSBP算法和频域加窗滤波的WFSBP算法的成像结果如图11(a), 11(b), 11(c)所示。由图可见，3种算法均可实现目标的成像，并正确反映目标的位置、形状和大小。比较3幅图可见，WFSBP算法的成像质量最高，较好地抑制了回波中高频噪声，目标点相对能量高，成像效果好。

图11 金属圆锥成像结果

5 结束语

频域加窗滤波球后向投影(WFSBP)算法，适用于大转角目标的高分辨成像，能够补偿转动角度离散化带来的数据误差的影响，并有效的抑制高频噪声，从而得到高质量高分辨率的目标图像。大转角形成的大的合成孔径，成像分辨率高，中心频率决定成像分辨率，而发射带宽不再是决定分辨率的主要因素，其决定图像的动态范围。

[1] 保铮, 邢孟道, 王彤. 雷达成像技术[M]. 北京: 电子工业出版社, 2005: 6-11.Bao Zheng, Xing Meng-dao, and Wang Tong. Radar Imaging Technique [M]. Beijing: Electronic Industry Press, 2005:6-11.

[2] 黄琼, 陈洁, 孟升卫, 等. 一种快速超宽带穿墙雷达成像算法[J]. 电子与信息学报, 2009, 31(8): 2001-2005.Huang Qiong, Chen Jie, Meng Sheng-wei,et al.. A fast imaging algorithm for UWB through-wall radar [J].Journal of Electronics&Information Technology, 2009, 31(8):2001-2005.

[3] Rovnakova J and Kocur D. UWB radar signal processing for through wall tracking of multiple moving targets [C].European Radar conference, Paris, France, Sept. 30-Oct. 1,2010: 372-375.

[4] Kidera S, Sakamoto T, and Sato T. High-resolution 3-D imaging algorithm with an envelope of modified spheres for UWB through-the-wall radars [J].IEEE Transactions on Antennas and Propagation, 2009, 57(11): 3520-3529.

[5] Huang Q, Meng S W, Wu S Y,et al.. Tracking and imaging algorithm of walking human bodies for ultra wideband radar[C]. International Conference on Electronic Measurement and Instruments, Beijing, China, Aug. 16-19, 2009, 290-295.

[6] Immoreev I. Practical application of ultra-wideband radars[C]. The Third International Conference on Ultrawideband and Ultrashort Impulse Signals, Sevastopol,Ukraine, Sept. 18-22, 2006: 44-49.

[7] Egor Z. UWB radar for detection and localization of trapped people [C]. International Radar Symposium, Vilnius,Lithuania, June 16-18, 2010: 1-4.

[8] Sakkila L, Rivenq A, and Tatkeu C. Methods of target recognition for UWB radar [C]. IEEE Intelligent Vehicles Symposium, San Diego, CA, June 21-24, 2010: 949-954.

[9] 何静. 高分辨ISAR转台成像MTRC的补偿算法研究[D]. [硕士论文], 西北工业大学, 2007.He Jing. High resolution ISAR rotation platform imaging [D].[Master dissertation], Northwestern Polytechnical University,2007.

[10] Kak A C and Slaney M. Principles of Computerized Tomographic Imaging [M]. New York: IEEE Press, 1988:60-74.

[11] 胡楚峰. 雷达目标RCS测试系统及微波成像诊断技术研究[D].[硕士论文], 西北工业大学, 2007.Hu Chu-feng. RCS measurement system of radar target and microwave imaging diagnosis technique research [D]. [Master dissertation], Northwestern Polytechnical University, 2007.

[12] Dean M, Glenn H, and Glen W. Aperture synthesis by object rotation in coherent imaging [J].IEEE Transactions on Nuclear Science, 1980, 27(2): 989-997.

[13] Sullivan R J. Microwave Radar Imaging and Advanced Concepts [M]. London: Artech House, 2000: 166-172.

[14] Amin M G and Ahmad F. Wideband synthetic aperture beamforming for through- the-wall imaging [J].IEEE Signal Processing Magazine, 2008, 25(4): 110-113.

[15] Nguyen L, Ressler M, and Sichina J. Sensing through the wall imaging using the Army Research Lab ultra-wideband synchronous impulse reconstruction radar [C]. Proc. of SPIE,2008, Vol. 6947, 69470B: 1-10.

[16] 粟毅. 冲激脉冲SAR成像理论与方法研究[D]. [博士论文], 国防科学技术大学, 2001.Su Yi. Impulse SAR imaging theory and algorithm research[D]. [Ph.D. dissertation], National University of Defense Technology, 2001.

[17] Thomas G, Flores B C, and Jae Sok-Son. SAR sidelobe apodization using the Kaiser window [C]. Proceedings of the IEEE International Conference on Image Processing, British Columbia, Canada, Sept. 10-13, 2000: 709-712.