一种适用于大区域稀疏控制点下的机载InSAR定标方法

胡继伟 洪 峻 明 峰 张林涛③

①(中国科学院空间信息处理与应用系统技术重点实验室 北京 100190)

②(中国科学院电子学研究所 北京 100190)

③(中国科学院研究生院 北京 100039)

1 引言

干涉合成孔径雷达(InSAR)可以全天时、全天候获取大面积高精度的高程信息及地表形变信息，因而广泛应用于地形3维测绘、环境监测及灾害评估等领域[1−3]。应用 InSAR 系统获取数字高程图(Digital Elevation Model, DEM)时，DEM精度对系统参量误差非常敏感，系统参量误差(基线误差，干涉相位偏置等)的存在严重影响高程测量精度，因而高精度的高程测量需要通过干涉定标来对这些系统参量误差进行校正。

在机载InSAR系统实用化大区域制图中，由于载机运动姿态的不稳定性导致不同景、不同条带的图像对应的干涉参量(基线矢量)是时变的，因而需要对不同景不同条带的图像对应的干涉参量分别进行定标。传统干涉定标相关研究多局限于对单景图像对进行处理[4−6]。一般对于单景图像至少需要 3个控制点(GCP)来进行干涉参量的估计，而干涉参量敏感度方程的病态性要求增加较多 GCP来减小干涉相位随机误差对定标精度的影响。对于复杂地形区域，野外布放GCP难度很大，部分区域可能只有少数控制点甚至没有控制点，对于这些区域传统干涉定标方法不再适用；另一方面，由于干涉参量偏差导致高程误差沿距离向具有空变特性以及不同条带干涉参量解算精度不一致，因而传统定标方法会造成条带间重叠区域高程不一致问题，增加了后续图像拼接的难度，不利于InSAR系统的实用化应用。

本文提出一种新的基于区域网平差理论的适用于大区域稀疏控制点下的机载InSAR定标方法。本方法将摄影测量学中的区域网平差理论引入到InSAR系统定标处理中[7]，充分利用各条带内GCP以及相邻条带间同名加密点(连接点，CP)，分别建立相应的误差关系模型，然后进行整体平差运算获得各条带校正后的系统参量，从而实现了稀疏控制点下InSAR系统高精度定标处理及系统误差校正，而且解决了传统定标方法导致的条带间重叠区域高程不一致问题。同时，在干涉参量联合定标处理时引入加权处理，减小法方程的条件数，从而提高干涉参量的解算精度。最后，通过对丘陵区域3条带仿真数据进行联合定标处理，验证了本文提出方法的有效性和合理性。

2 基于区域网平差理论的InSAR定标算法

由InSAR测高原理，目标点高程可表示为

其中，标准模式下，P=1，“乒乓模式”下，P=2。

目标点高程用符号形式可表示为

将式(2)进行泰勒级数展开线性化可得

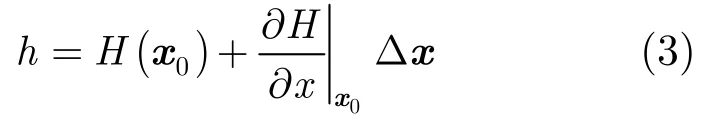
对各条带内所有GCP和同名CP分别列出相应误差方程，对于GCP，高程h已知，因而误差方程可表示为

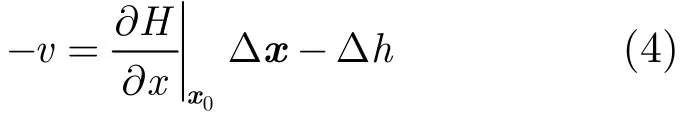
同名CP，即条带间重叠区域对应相同目标点，可通过特征点提取和最优相关匹配技术来实现高精度的同名点提取[8,9]。对于CP，由于高程h未知，可将h表示为h0+dh，其中，h0为CP高程初始参考值，dh为未知高程偏差，则CP误差方程可表示为

以3条带为例分析，各条带内所有参考点(GCP和CP)如图1所示。对所有条带内GCP和CP根据式(4)和式(5)列误差方程式，写成矩阵形式分别为

图1 3条带参考点布设示意图

对GCP：

对CP：

用符号形式可表示为

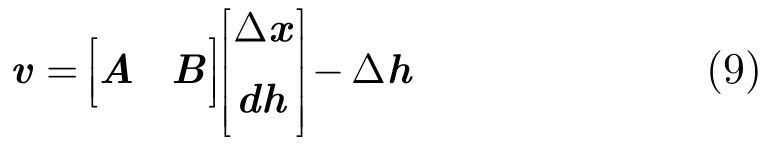
其中Δx及dh为未知参量。

由误差方程式(9)可列出下面的方程式

即

用符号表示为

我们的目的是求解干涉参量误差Δx，因而将式(12)展开并消去dh可得

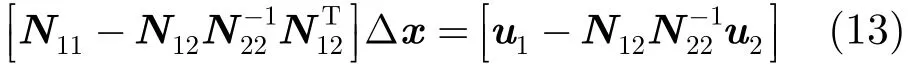
用符号可表示为

根据式(14)由广义逆法即可求得超定线性方程组的最小二乘解，即干涉参量误差Δx为

其中+F为矩阵F的广义逆矩阵。

在干涉参量误差求解过程中，由于各干涉参量的敏感度存在加大差异，导致敏感度矩阵存在病态性[7]，将不同干涉参量敏感度系数进行加权处理，从而降低敏感度矩阵条件数，提高干涉参量误差解算精度[10]。

敏感度矩阵A可表示为

各干涉参量的加权系数为其敏感度数量级的倒数，即

则加权后敏感度矩阵为

经加权处理后，各干涉参量敏感度趋于接近，敏感度矩阵条件数减小，病态性得到改善。

3 仿真实验结果与分析

3.1 实验数据

本文通过对机载 InSAR仿真数据进行实验来验证本文提出的算法的有效性。实验数据由中国科学院电子学研究所提供，使用2009年在西安地区飞行的实测pos数据和姿态数据，仿真了丘陵地区机载双天线InSAR系统3条航带的数据，InSAR主要系统参数如表1所示。仿真场景区域5 km×5 km，条带间重叠度30%，场景及地面强点目标设置如图2所示。其中，第1条带和第3条带包含146个强点目标，第2条带214个强点目标，第1条带、第2条带重叠区域以及第2条带、第3条带重叠区域各90个强点目标。3条带图像及强点目标分布如图3所示。

表1 InSAR系统参数

图2 仿真丘陵区域示意图

图3 仿真3条带图像及强点目标分布示意图

3.2 传统定标方法和联合定标方法结果与分析

分别采用传统干涉定标方法和联合定标方法对各条带进行定标处理，控制点选取方式如图4所示。其中，第1条带选取5个GCP，第2条带选取3个GCP，第3条带选取5个GCP，其余目标点作为检查点。考虑到实际测量误差，以下所有实验对控制点均加入均值为0，方差为0.1 m高斯随机误差。分别对3条带数据进行干涉定标处理，结果如表2所示。

图4 控制点选取方式示意图

表2 传统干涉定标方法和联合定标方法结果

由实验结果可得到如下结论：

(1)各条带单独进行干涉定标处理时，由于干涉相位噪声、控制点测量误差等因素的存在，在GCP个数较少时，敏感度矩阵的病态性导致干涉参量解算误差较大，进而导致目标点高程误差较大。由于干涉参量偏差导致高程误差沿距离向具有空变特性以及不同条带干涉参量解算精度不一致，因而导致相邻条带重叠区域目标点高程相对误差较大，增加了后续图像拼接的难度。

(2)相对于传统定标方法，基于区域网平差理论的联合定标方法高程精度显著提高，由于将多条带GCP和CP进行联合定标处理增加了参考点，因而降低了干涉相位噪声、控制点测量误差等随机误差的影响，提高了各条带干涉参量解算精度及目标点高程精度。另一方面，由于条带间重叠区域高程由较多CP进行约束，因而定标处理后条带间重叠区域高程误差显著减小，且各条带高程误差很接近，便于后续图像的拼接，进一步验证了本文提出的定标方法的优点及合理性。

3.3 稀疏控制点下联合定标方法结果与分析

稀疏控制点下分别选取不同个数的 GCP对各条带进行联合定标处理，控制点选取方式及定标结果如图5和表3所示。由图可知，各条带只有少数甚至没有控制点，因而传统干涉定标方法不再适用。

图5 稀疏控制点下不同控制点选取方式示意图

表3 稀疏控制点下联合干涉定标方法结果

对稀疏控制点下不同控制点选取方式实验结果进行分析可得到如下结论：

(1)稀疏控制点下，虽然各条带GCP数不满足传统定标方法需求，采用本文提出的基于区域网平差理论的联合定标方法仍然可以实现多条带联合定标处理，并且精度要优于传统定标方法，主要是由于将多条带GCP和CP进行联合定标处理增加了参考点，而且还降低了随机误差对定标结果的影响。

(2)比较几种不同的 GCP选取方式定标结果可以看出，控制点数减少时，高程误差会逐渐增大，并且结果受GCP选取策略影响。选取方式1精度最高，主要由于各条带均有分散的GCP，因而整体联合解算时各条带误差均能得到控制。比较选取方式2和方式3可以看出，相同GCP个数下选取方式2结果要稍优于选取方式 3，主要因为选取方式 2条带3也有控制点因而条带3误差得到控制，而由于整体求解，因而条带1控制点减少对于结果影响较小。由选取方式4结果可以看出，第2、第3条带均没有控制点时，随着条带数增加高程误差会逐渐放大，主要由于干涉参量偏差导致高程误差随距离向增加而增大，仅依靠 CP高程传递来进行定标高程误差会不断积累，但由于采用多条带GCP和CP联合定标处理，当传递条带数较少时误差仍然可以控制在一定范围内。实际应用时，最好各条带有少量控制点或者无控制点条带间隔较少，如选取方式1、2和选取方式3，这样可以抑制高程误差不断增大的趋势。另一方面，由于重叠区域有较多CP约束，因而几种选取方式重叠区域高程误差基本不变，便于后续图像拼接。

4 结束语

InSAR系统需要通过干涉定标来校正干涉参量误差以提高 DEM 获取精度，传统干涉定标方法需要较多人工控制点，不利于InSAR系统的实用化应用。而本文提出的基于区域网平差理论的机载InSAR定标方法可以实现大区域稀疏控制点下InSAR系统高精度定标处理及系统误差校正，而且解决了传统干涉定标方法导致重叠区域高程不一致的问题。通过对丘陵区域3条带仿真数据进行区域联合定标处理，验证了本文提出方法的有效性及合理性，可以作为一种新的实用的大区域机载InSAR定标方法。

同名 CP提取是实现多条带联合定标处理的关键之一，后续工作还需要考虑如何提高同名点提取精度；另一方面，需要分析稀疏控制点下GCP的选取策略及其对联合定标结果的影响，从而提出稀疏控制点下GCP的最优布点方案。

[1] Madsen S N and Zebker H A. Topographic mapping using radar interferometry: processing techniques[J].IEEE Transactions on Geoscience and Remote Sensing, 1993, 29(6):1125-1128.

[2] Rosen P A and Hensley S,et al.. Synthetic aperture radar interferometry [J].Proceedings of the IEEE, 2000, 88(3):333-381.

[3] Krieger G and Hajnsek I,et al.. Interferometric synthetic aperture radar (SAR) missions employing formation flying[J].Proceedings of the IEEE, 2010, 98(5): 689-696.

[4] Mallorqui J J, Bara M, and Broquetas A. Calibration requirement for airborne SAR interferometry [C]. SAR Image Analysis, Modeling and Techniques III, Proc. SPIE, 2000,4173: 267-278.

[5] 李品, 王东进, 陈卫东. 基于定标器高程差的 InSAR 参数定标[J]. 中国科学院研究生院学报, 2009, 26(1): 68-74.Li Pin, Wang Dong-jin, and Chen Wei-dong. Parameter calibration based on calibrator height difference for InSAR system [J].Journal of the Graduate School of the Chinese Academy of Sciences, 2009, 26(1): 68-74.

[6] 张薇, 向茂生, 吴一戎. 基于三维重建模型的机载双天线SAR外定标方法及实现[J]. 遥感技术与应用, 2009, 24(1): 262-269.Zhang Wei, Xiang Mao-sheng, and Wu Yi-rong. Realization of outside calibration method based on the sensitivity equation for dual-antenna airborne SAR[J].Remote Sensing Technology and Application, 2009, 24(1): 262-269.

[7] 王之卓. 摄影测量原理[M]. 北京: 测绘出版社, 1984: 68-74.Wang Zhi-zhuo. Photogrammetry Theory [M]. Beijing:Publishing House of Photogrammetry, 1984: 68-74.

[8] 张薇. 机载双天线干涉SAR定标方法研究[D]. [博士论文], 中国科学院电子学研究所, 2009.Zhang Wei. Airborne dual-antenna InSAR's interferometric calibration method research [D]. [Ph.D. dissertation],Institute of Electronics, Chinese Academy of Scienses, 2009.

[9] 韩松涛, 向茂生. 一种基于特征点权重的机载 InSAR系统区域网干涉参数定标方法[J]. 电子与信息学报, 2010, 32(5):364-370.Han Song-tao and Xiang Mao-sheng. A bundle adjustment calibration method for aireborne syetem based on weighting of feature points [J].Journal of Electronics&Information Technology, 2010, 32(5): 364-370.

[10] 李庆扬, 王能超, 易大义. 数值分析[M], 第 4版. 北京: 清华大学出版社, 2006: 74-76.Li Qing-yang, Wang Neng-chao, and Yi Da-yi. Numerical Analysis[M]. Fourth Edition, Beijing: Publishing House of TsingHua University, 2006: 74-76.