无偏置ν- SVM分类优化问题研究

丁晓剑 赵银亮

(西安交通大学电子与信息工程学院 西安 710049)

1 引言

C-SVM(Support Vector Machine)起源于文献[1]提出的支持向量网络(support vector networks)。在一般的神经网络结构中，只需调节输出向量和隐藏层连接的权重向量w就可以较好地拟合训练样本，而文献[1]指出需要调节向量w和(b)才能得到最优分类超平面，但在文中并没有提到(b)存在的意义。Poggio等人[2]从核函数的正定理论分析得出如果核函数是正定的(positive definite)，在SVM优化问题中是不需要(b)的，文献[3]指出使用高斯核(gaussian kernel)等常用核函数的SVM优化问题不需要(b)。Huang等人[4]提出了优化极限学习机(Extreme Learning Machine, ELM)的分类方法，指出优化极限学习机的模型和C-SVM是等价的，决策函数倾向于通过原点，即不需要(b)的存在。文献[5]研究了(b)对C-SVM分类优化问题泛化性能的影响，在实验中验证得到无(b)C-SVM优化问题的泛化性能更好，对参数C不太敏感，计算代价更小等一系列性质。虽然ν-SVM[6,7]与C-SVM的目标优化问题不同，约束条件也不同，但两者得到的最优分类超平面是等价的，即文献[5]的结论应该适用于ν -SVM。本文首先给出无(b)ν-SVM优化问题的描述，然后给出了利用有效集方法求解无(b)ν-SVM优化问题的子优化问题求解方法，在标准数据集上的多个指标的性能分析得到了理想的效果。

2 无(b)v-SVM优化问题

给定一个含有m个样本的训练样本集{xi,，其中输入为d维向量x∈Rd，输出为y∈iiR。通常训练样本集在输入空间中是线性不可分的，需要引入映射函数φ(x)将xi映射到高维空间 φ(xi)中。训练无(b)ν-SVM分类问题等价于求解如下优化问题：

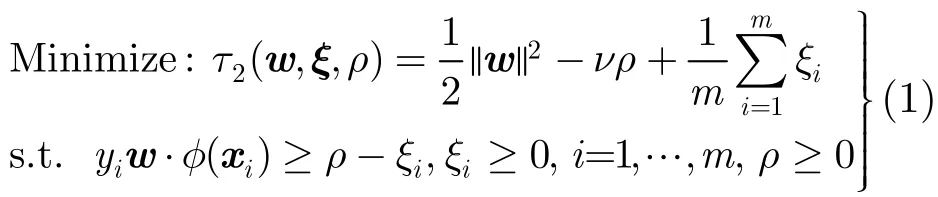
引入拉格朗日函数：

其中 αi, βi, δ为非负拉格朗日乘子。

对L关于变量w,ξ,ρ求偏导数，下列条件都满足时得到式(1)的最优解：

将式(3)和式(4)代入拉格朗日函数L，可得无(b)ν-S VM 的对偶优化问题：

2.1 Karush-Kuhn-Tucker条件

为了得到原始优化问题式(1)的最优解，需要推导出它的完整Karush-Kuhn-Tucker(KKT)条件：

初始可行性：

对偶可行性：

对偶与原问题的补条件：

由于f(x)为无(b)ν-SVM的决策函数，令fi为无(b)ν-SVM分类器对样本xi预测的值，并有fi=由最优解条件和补条件可得

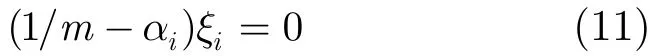
如果 αi=0，由式(11)可知 ξi=0，由最优解条件和δρ=0可知ρ=0，再由式(8)可知fi≥ ρ ，进而有fi≥ 0。如果 αi=1/m，由式(10)可知fi−ρ+ξi=0，由最优解条件和补条件δρ=0可知ρ=0，又由式(8)可知fi=−ξi≤ 0。如果0 ＜αi＜1/m，由补条件式(10)可知fi−ρ+ξi=0，由式(11)可知 ξi=0，再由式(8)可知fi=ρ≥ 0。综上，式(3)的最优解满足下列条件：

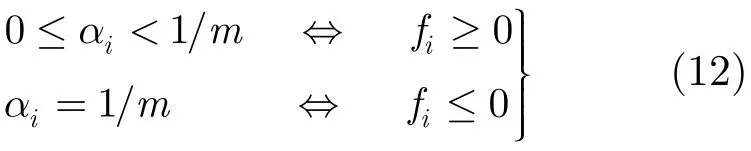
3 优化问题求解方法

文献[8]利用有效集算法来求解C-SVM优化问题，该有效集算法将C-SVM对偶优化问题分解为一系列子优化问题来求解，其主要计算代价是每次迭代过程中求解子优化问题，是一种高效简便的算法。由于无(b)ν-SVM的对偶优化问题都与C-SVM对偶优化问题不同，文献[8]中的有效集算法无法直接应用，在本节将推导无(b)ν-SVM子优化问题的求解方法。

式(8)为无(b)ν-SVM的对偶优化问题，为方便推导求解，将式(8)写成下面紧凑的形式：

其中H=KYYT∈RN×N,K为式(7)中对应的核矩阵，

同样由向量α0,αm的定义可知α0,αm元素的值是固定的，求解式(13)等价于求解下式：

其中Hww和Hwm为H的子矩阵，行和列相应的集合Sm和Swork标识。同理由于式(14)是对αwork求最小值，由αwork的定义可知αwork中分量的值都在区间(0,1/m)中，即约束0 ≤ αi≤ 1/m必然满足，这样式(14)就变为等式约束优化问题：

其中δ=αwork,Q=Hww,c=Hwmαm,A=[1,… ,1]T∈Rn,n为αwork中元素的个数，t=ν−∑αm。

式(13)可以通过解条件问题的乘子法来求解，构造拉格朗日函数：

令L1(δ,λ)对δ和λ的导数为零，得到线性方程组：

现已将无(b)ν-SVM子优化问题转化为与C-SVM 子优化问题相同的形式。有效集算法利用2层循环来求解目标优化问题式(13)：外循环判断α中边界约束元素是否都满足KKT条件式(12)，如果都满足，算法终止。如果不满足，则选取违反KKT条件的变量进入内循环求解；而内循环目标是求解子优化问题式(15)，使得最优解αwork满足上下界约束。

4 实验与结果分析

为了研究(b)对ν-SVM分类性能的影响(本文仅讨论两类分类问题)，本文将用有效集算法对ν -SVM (nu-AS)和无(b) ν-SVM(nbnu-AS)进行多个指标的比较，算法是在 Pentium 4, 2.53 GHz,CPU, MATLAB 2007环境下实现，实验数据集分别来自UCI数据库[9]，Statlog数据库[10]，所有样本的输入都归一化到[0,1]之间。

4.1 参数设定

对于nu-AS算法和nbnu-AS算法性能比较使用高斯核(注：此处公式已作改动)作为核函数，需要合适的核参数和代价参数ν才能得到尽量好的分类性能。代价参数ν的选择按照文献[6]的选择方法，10个参数ν值分别取：0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0。对高斯核，对于每个数据集选取15个γ值和10个ν值，共有150种参数对，并选择性能最好的组合(ν, γ)，参照文献[11]中的参数选择方法，15个γ值分别取：0.001, 0.01, 0.1, 0.2, 0.4, 0.8, 1, 2, 5, 10, 20, 50, 100,1000, 10000。对于每个数据集采用50次测试，每次测试随机训练样本数目和测试样本数目。实验指标包括平均训练时间(ATT)，平均测试精度(ATA)，标准方差(DEV)和平均的支持向量数目(ASV)。

4.2 实验性能比较

表1是nu-AS和nbnu-AS算法的性能指标比较。在13个数据集中，nbnu-AS算法在其中10个数据集上的平均测试精度要好，nu-AS算法在Monk’s Problem 1数据集上的平均测试精度要好，在另外两个数据集上两个算法的平均测试精度一致。两个算法在所有数据集上的平均训练时间相差都不大。

表1 标准数据集上的性能比较

ν-S VM和无(b)ν-SVM的求解是将原始优化问题转化为对偶优化问题来求解，由于对偶间隙的存在，对偶优化问题的最优解并非一定为原始优化问题的最优解。尽管无(b)ν-SVM在Monk’s Problem 1数据集上得到更小的函数值(见表2)，但是无(b)ν -SVM得测试精度仍然低于ν-SVM。

4.3 ν-SVM和无(b)ν-SVM优化问题最优解比较

由于ν-SVM优化问题与无(b)ν-SVM优化问题多出一个约束条件：TY=0α，从优化问题的解空间上分析后者应该能得到比前者更优的解。本节从实验上分析该约束条件对优化问题最优解影响，利用有效集算法和最优函数值指标对两个优化问题进行比较。为了使两个目标优化问题相同(约束条件不同)，nu-AS和nbnu-AS的参数须设置一致(从而优化问题中的核矩阵也相同)，在此将两个算法的参数对都设为nu-AS的最优参数对，表2为比较结果。在前10个数据集上，nu-AS算法在两个核函数上都取得了更优的解，而在后3个数据集上，两个算法在两个核函数上的最优解都相同。设nu-AS算法的解空间为S1, nbnu-AS算法的解空间为S2，则有S1⊆S2。

表2 nu-AS和nbnu-AS算法的最优函数值比较

4.4 参数敏感性分析

本节比较核参数和代价参数ν对算法测试精度的影响，实验数据选取Pwlinear数据集，高斯核的参数值按照4.1节选取。

从图1和图2可以看出，nu-AS在高斯核上的不同参数选取对于测试精度影响很大，而且没有规律。nbnu-AS算法则对参数ν不太敏感，曲面比较光滑。在实际参数选取中，对于参数ν可以扩大参数选取值的间隔，利用较少的参数值对就可以找到最优测试精度。

图1 nu-AS在高斯核上的测试精度

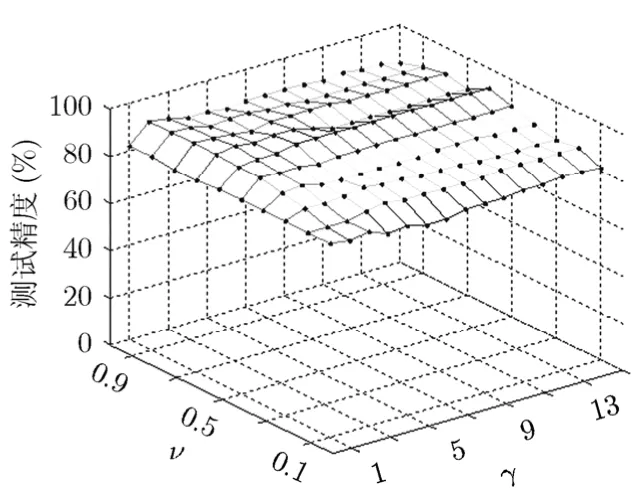
图2 nbnu-AS在高斯核上的测试精度

5 结束语

由于ν-SVM引入了有实际意义的参数ν，在机器学习的各个领域中有广泛的应用和实际的指导意义。本文研究对比了ν-SVM和无(b)的ν-SVM优化问题，从多个性能指标的实验上分析得出无(b)的ν -SVM 的泛化性能要好于ν-SVM，在同等目标优化问题下ν-SVM只能得到无(b)的ν-SVM的次优解，无(b)的ν-SVM对参数ν不太敏感，在较少的参数值对中就可以找到最佳的测试精度。

本文的工作适用于ν-SVM的改进算法，可以将无(b)的ν-SVM应用于现有的对ν-SVM进行改进的算法。在以后的研究工作中将无(b)的ν-SVM应用于文本挖掘，图像识别等实际领域中，进一步验证无(b)的ν-SVM的有效性。

[1] Cortes C and Vapnik V. Support vector networks.Machine Learning, 1995, 20(3): 273-297.

[2] Poggio T, Mukherjee S, Rifkin R,et al.. “b”. (A.I. Memo No.2001-011, CBCL Memo 198, Artificial Intelligence Laboratory,Massachusetts Institute of Technology), 2001.

[3] Evgeniou T, Pontil M, and Poggio T. Regularization networks and support vector machines.Advances in Computational Mathematics, 2000, 13(1): 1-50.

[4] Huang G B, Ding X J, and Zhou H M. Optimization method based extreme learning machine for classification.Neurocomputing, 2010, 74(1/3): 155-163.

[5] 丁晓剑, 赵银亮. b对支持向量机分类问题泛化性能的影响.自动化学报, 待发表.

[6] Schölkopf B, Smola A J, Williamson R, and Bartlett P L.New support vector algorithms.Neural Computation, 2000,12(5): 1207-1245.

[7] 王娜, 李霞. 基于类加权的双ν支持向量机. 电子与信息学报,2007, 29(4): 859-862.Wang Na and Li Xia. A new dual ν support vector machine based on class-weighted.Journal of Electronics and Information Technology, 2007, 29(4): 859-862.

[8] Scheinberg K. An efficient implementation of an active set method for SVMs.Journal of Machine Learning Research,2006, 7(10): 2237-2257.

[9] Blake C L and Merz C J. UCI repository of machine learning databases. http://www.ics.uci.edu/～mlearn/MLRepository.html, Department of Information and Computer Sciences,University of California, Irvine, USA, 2010.

[10] Michie D, Spiegelhalter D J, and Taylor C C. UCI Machine Learning Repository: Statlog Data Set, available: http://archive.ics.uci.edu/ml/datasets/Statlog+(Landsat+Satellite),2010.

[11] Ghanty P, Paul S, and Pal N R. NEUROSVM: an architecture to reduce the effect of the choice of kernel on the performance of SVM.Journal of Machine Learning Research,2009, 10(3): 591-622.