衰落信道盲接收条件下的调制分类

崔伟亮 李剑强 江 桦 黄文芳

(解放军信息工程大学 郑州 450002)

1 引言

调制分类是指对接收信号自动处理并判定调制类型的过程。作为信号检测与解调的中间步骤，自动调制分类技术在各种民用及军事应用中扮演着重要角色，如感知无线电，智能解调器，电子侦察等，该技术已被考虑纳入未来自适应通信标准[1]。相关研究已经超过10年，成果可分为两类：一类是基于似然比函数判定的方法，另一类是基于特征判别的方法。算法至少包括信号预处理和分类器判决两步骤[2]。

由于噪声以及信道等因素的影响使信号识别的难度加大，如何在衰落信道环境中，特别是低信噪比衰落信道中实现调制识别是该领域研究难点。适于衰落信道条件识别算法有：基于似然比判别的方法，如文献[3]提出了混合似然比函数判别算法，通过对匹配接收后的信号估计矩，完成噪声功率、衰落系数、相位的估计，结合似然比函数实现平衰落信道下的PSK和QAM信号识别。有基于累积量的方法，文献[1,4]提出了基于改进的四阶或六阶累积量信号识别算法，利用匹配接收后的信号计算累积量，完成多径衰落信道下调相和幅相信号的有效分类。还有基于循环统计量的方法，如文献[5,6]提出了通过计算同步接收后信号的循环累积量，并结合多天线技术，实现了在平衰落信道未知相位及定时误差的条件下，ASK, PSK及QAM信号的稳健分类。从已有方法看，大部分要求对信号进行同步接收后进行分类，需要进行参数估计、定时同步、载波恢复等处理步骤。要达到理想的分类效果，对预处理要求偏高。在非合作接收场合，特别是低信噪比衰落信道环境中，由于处理条件差、先验信息少，预处理精度难以达到要求，算法分类效果不佳。

为了提高衰落接收环境下的信号分类能力，降低识别算法预处理要求，由信号检测中循环平稳相关方法启发[7,8]，本文提出了一种基于循环平稳性检测的信号识别方法。通过利用不同调制信号循环频率特征上的差异，结合循环平稳性检测，完成调制类型的判别。实现衰落信道多种常见数字信号的分类。算法不必进行载波频率、符号周期等参数估计，无需定时、载波同步等预处理过程；同已有循环累积量识别算法相比，能对FSK, MSK, OFDM等非线性调制信号进行区分，对噪声及衰落信道敏感度更低，有效提升分类效果。

全文安排如下，首先对算法所涉及信号模型、循环统计量基本概念进行介绍，然后提出分类特征，在给定算法及循环平稳性检测实现步骤基础上，最后通过实验来完成相关算法的性能比较与分析。

2 信号模型

设基带接收信号r(i)(t)，存在相偏θc，频偏fe，定时偏差t0，加性复高斯噪声w(t)和多径衰落信道(径数为P)影响，表示为

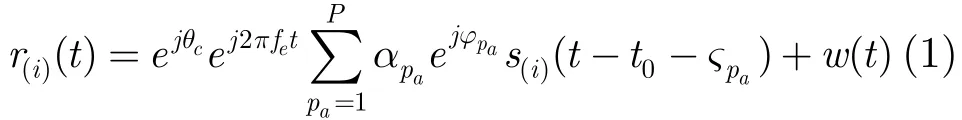
式中A表示信号的幅度，Ts表示符号周期，分别表示PSK/QAM, FSK, MSK信号第k个传输符号，sn,k表示OFDM信号第n个子载波k个周期时所传输符号。符号所对应序列零均值独立同分布。和fd分别为FSK信号阶数和频移大小，为 PSK或 QAM 对应的符号序列。OFDM的，其中Tu=1/ΔfN表示有用符号时间宽度，N为OFDM子载波数，Tcp为循环前缀长度。MSK信号g(t) =qMSK(t) ⊗h(t)；其它信号g(t)=q(t)表示脉冲成型滤波器，qMSK(t) =sin(πt/2Ts),0 ≤t≤ 2Ts。

3 信号循环统计量

调制信号具有循环平稳特征，高阶循环统计量可表示这些特征。假设x(t)为一个连续时间n阶循环平稳复信号，则x(t)的n阶时变矩mx(t;τ)n,q为周期函数，用傅里叶级数展开，其系数即为该序列的n阶循环矩mx(β;τ)n,q：

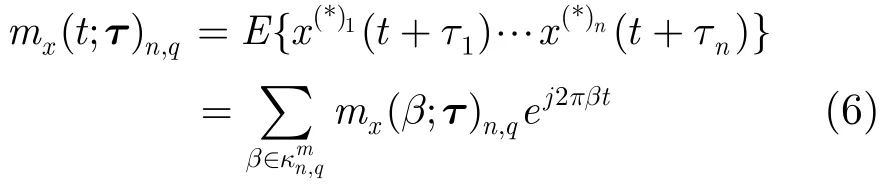
式中E{·}表示期望，(*)u,u=1,… ,n表示对数值可能取 共轭， 共 轭操 作 的总 数 为q,τ={τ1=0,τ2,…, τn}表示n维时延矢量。≠ 0}为mx(t;τ)n,q的循环频率集。则n阶循环矩的定义为

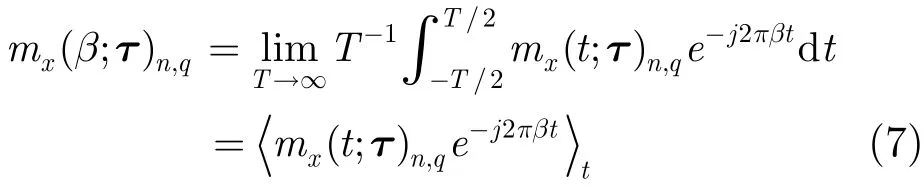
需要指出在时间段(FOT)的概率模型[7]下，式(7)可表示为

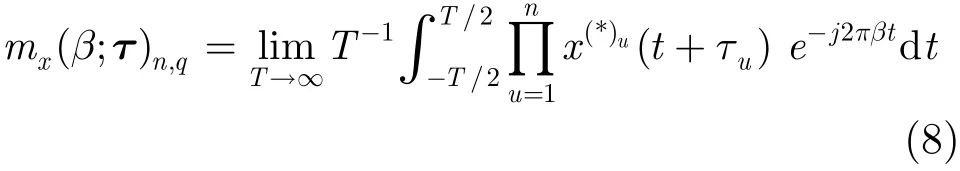
同理x(t)的n阶循环累积量cx(β;τ)n,q可以定义为

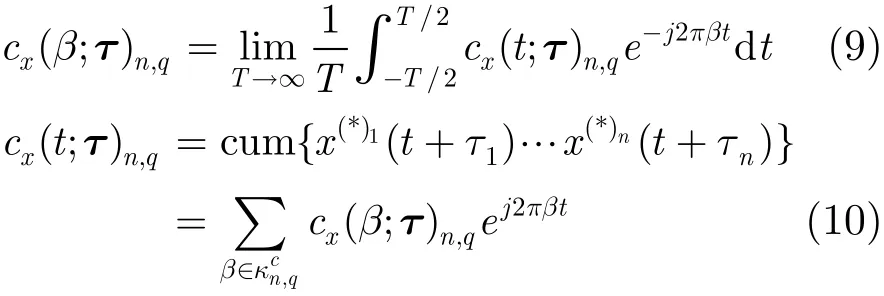
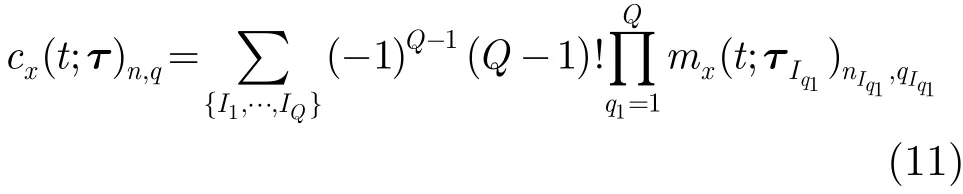
4 基于循环统计量的特征

(1)特征 1：mr(β)1,0的循环频率 文献[8]利用mr(β)1,0特征实现AWGN信道中FSK信号检测，本文推导衰落信道下的情况，用于FSK信号的区分。r(t)的一阶时变矩mr(t)=E[r(t)]，对于FSK信号，

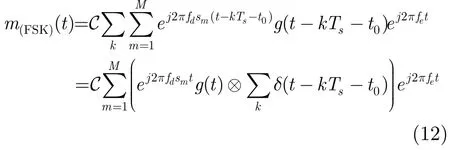
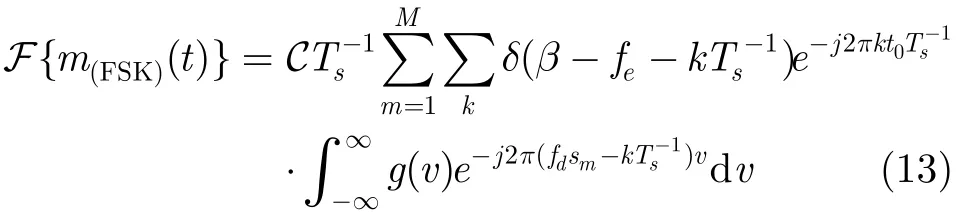
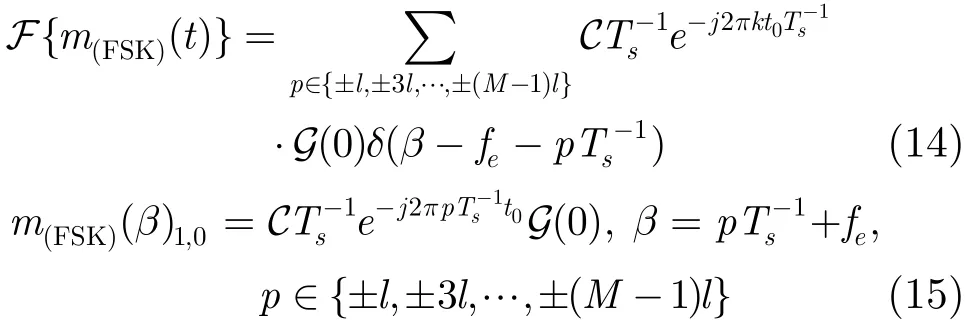
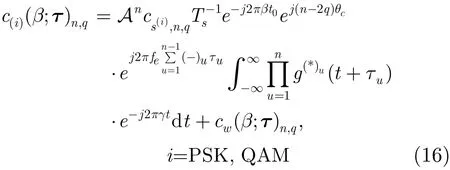
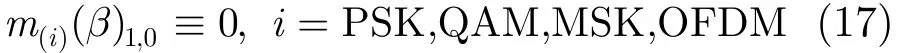
由以上分析，循环矩的循环频率特征可将 2FSK,4FSK与其它信号区分出来。

(2)特征 2：cr(β,τ)2,1的循环频率 参考文献[10]的二阶一次共轭循环累积量特征，实现 CPOFDM信号的区分。当n=2,q=1时，由式(16)可得

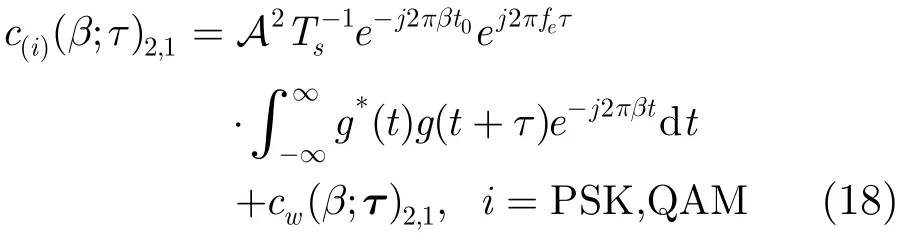
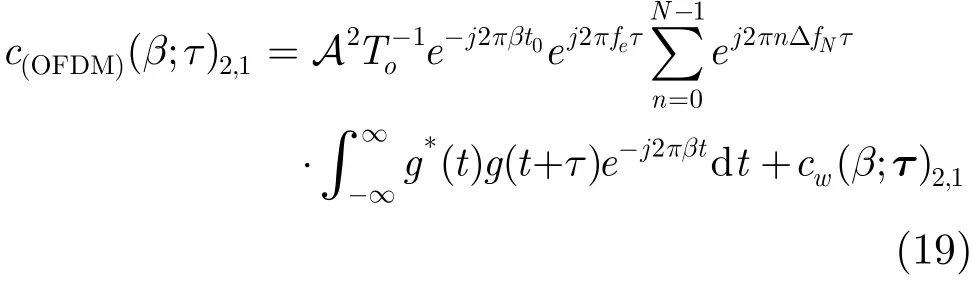
(3)特征 3：cr(β, τ)2,0的循环频率 当n=2,q=0时，由式(16)可得

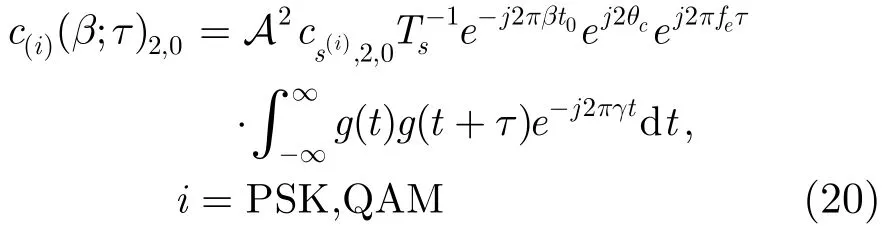
当i=BPSK，二阶累量cs(BPSK),2,0=1,i=8PSK,QAM,=0[9]。所以cr(β, τ)2,0：

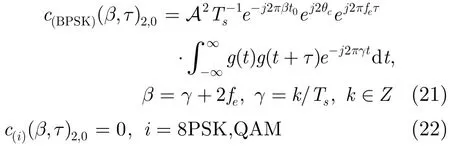
对于MSK信号，由式(20)，得

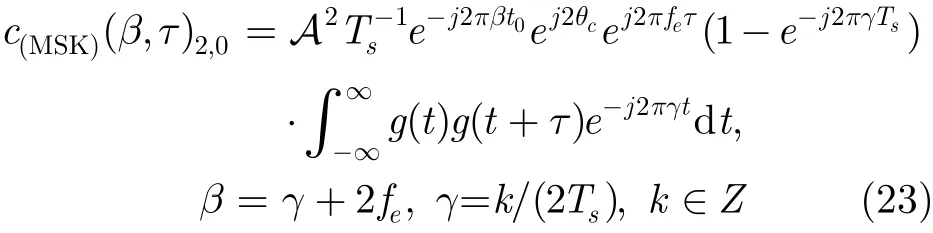
因此cr(β, τ)2,0的循环频率特征可将MSK, BPSK与8PSK和QAM信号区分出来。

(4)特征 4：cr(β,τ)4,0的循环频率 当n=4,q=0时，由式(16)得

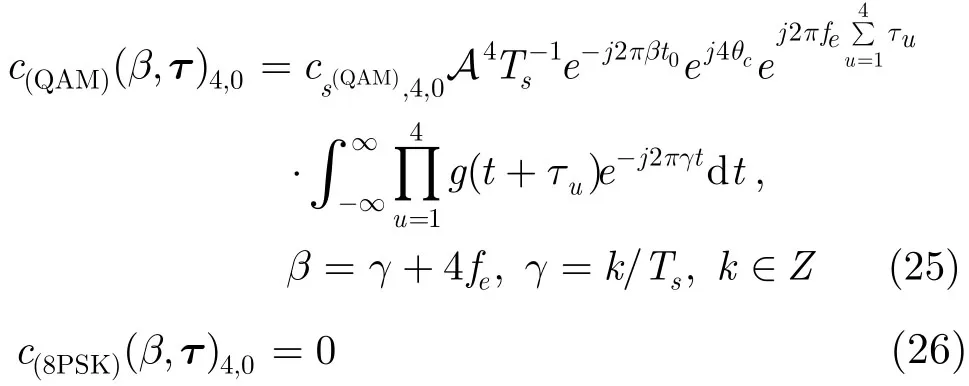
5 分类算法

假设为射频接收信号，信号需进行下变频及离散采样。算法对频偏不敏感，下变频时只需根据信号频谱中心来粗略给定下变频频率。同时为了门限归一化，数据要功率归一化(数据除以样本方差)。设采样率为fsa，对于单载波信号，ρ为每符号所含样点数。对于多载波信号，ρ为每子载波符号所含样点数，ρ≥2。接收信号离散采样得到算法具体步骤如下。

5.1 算法步骤

算法共需经过4个判断节点，识别过程如下：

节点 1：利用特征 1，实现2FSK,4FSK与其它信号的区分，处理步骤如下：

(1)计算接收信号r[k]的一阶循环矩量设样本长度为K，则

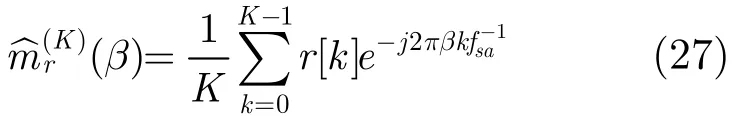
(2)由式(15)得，FSK信号的一阶循环矩在循环频率为处存在取值，取值的个数与调制阶数相同。假定估计门限VFSK，如果中点的幅度超过估计门限即得循环频率的估计。对中的每个取值，进行循环平稳性检测(具体方法见下节)，门限由预设误检测概率PF确定。

(3)判断集合中通过检测的个数为 2，则该信号为2FSK信号，如果个数等于4，则识别为4FSK信号。如果通过检测的个数为0，信号属于其它类型，则进入节点2。

节点2：利用特征2，完成OFDM信号与剩余其它信号的区分，步骤如下：

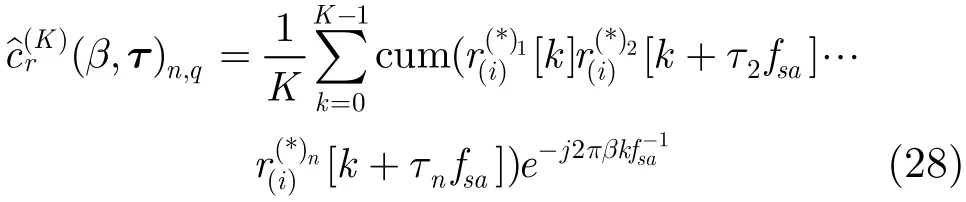
节点3：使用特征3完成BPSK，MSK的识别。利用式(28)计算信号的，分别在[B'/2,−0]和(0 ,B'/2]1)B'可由频谱所在范围粗略完成，由于频谱精度及脉冲成型等情况的影响，估计会存在误差，因此需根据相应情况适当调整搜索区间，防止因漏搜使算法失效。两个区间搜索最大值作为循环频率估值，然后对中的两个值在τ=0的情况下进行循环平稳性检测。如果两个频率均存在循环平稳性，则判定为MSK信号，存在一个循环频率，判定为BPSK信号，均不是进入下一节点判断。

需指出：除特征2 外，特征截面计算，均可利用FFT算法提高计算效率。

5.2 循环平稳检测

循环平稳性检测是一种盲检测算法，它能够验证循环累积量(或者循环多谱)，在循环频率的估计处是否具有循环平稳性[11]。在时延为τ的条件下，设H0表示不是信号的循环频率，H1表示是信号的循环频率。进行如下检验：

(1)由长度为K点的样本，计算n阶q次共轭循环累积量，记为算法中节点 1：n=1,q=0，节点2：n=2,q=1，节点3：n=2,q=0，节点 4：n=4,q=0。除节点 2外，其余节点τ均为0。利用构造如下矢量：

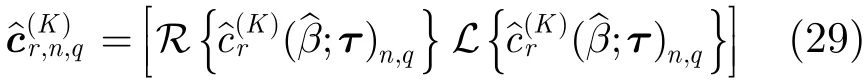
其中R{·}和L{·}分别表示取实部与虚部操作。

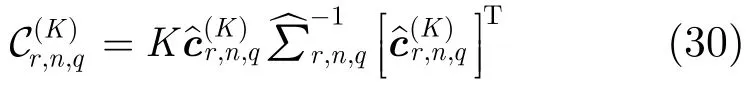
式中 [·]−1和[·]T分别表示矩阵的逆和转置。式中的表示系数矩阵，可由式(31)计算得到

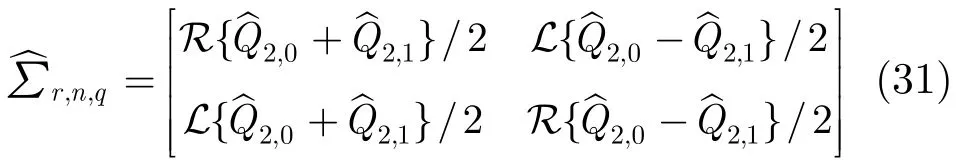
的表达式分别为

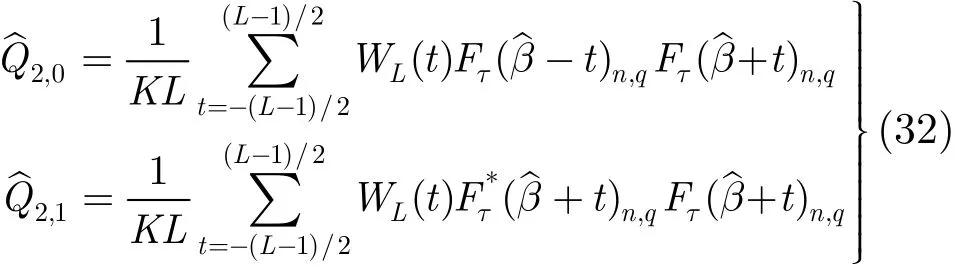
6 分类结果及性能分析

6.1 仿真条件

[4]，衰落信道条件如下：P=4, αpa满足v=0.8，方差=0.05莱斯分布，φ 满足

pa(0,2π]内均匀分布，ςpa在[0,500μs]内随机选取，噪声满足复高斯分布，随机系数样本长度内不变。除特殊说明外，信号条件如下：单载波信号1/Ts为1500 baut(波特)，频偏fe=200 Hz，初始相位θc为(−π,π]随机变化，t0为0.6Ts；均方升余弦成型滤波器，滤波器系数为0.35, FSK频移fd=1/Ts。OFDM信号内层调制为 QAM 或 PSK,Tu=64/1500 s,Tcp=16/1500 s,To=80/1500 s ,fsa为24 kHz。

6.2 实验结果与性能分析

实验 1 对经过衰落信道的各种信号循环累积特征的幅度进行估计，估计前经过滤波，图1(a)与图1(b)是MSK和8 PSK信号的cr(β,τ)2,0幅度谱，SNR分别为-15 dB和 30 dB。由式(23)知 MSK|cr(β,τ)2,0|在带宽范围内存在2个循环频率，式(22)知8PSK信号cr(β,τ)2,0恒为零，在图1(a)看到2根明显的离散谱线，而图1(b)中没有。图1(c)是4 QAM的|cr(β,τ)4,0|,SNR=-5 dB。根据式(25)，QAM在4倍频偏附近存在离散取值，图中结果与理论分析相一致。在设定的实验环境中，各特征均表现出良好的识别性能。

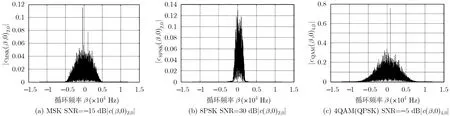
图1 经过衰落信道的循环累量幅度谱

实验 2 对衰落信道下信号在各节点识别性能进行测试，符号数均为1500。算法的循环平稳性检测中选取长度为61的Kaiser窗(窗参数为10)，节点1中估计门限为0.35。各节点检测门限Γ(l):Γ(1)=Γ(3)=Γ(4)=13.816,Γ(2)=18.412对应的误警概率为10−3,10−4。定义节点平均识别正确率Pc(l),l=1,…, 4用于衡量算法的识别性能。其中分别为节点l识别信号类型数和对应类型的识别正确率。以节点1为例：QAM包含为4 QAM和16 QAM两种信号。(实验中得到每个均进行1000次蒙特卡洛试验，下同。)

从图2结果看，在本文设定的信号信道环境中，节点1能够将SNR=-17 dB以上FSK信号与其它信号正确区分出来，平均识别正确率大于 90%；节点 2和节点 3能将 SNR=-10 dB以上的 OFDM,QPSK, MSK区分出来，平均识别正确率大于95%；节点4能将SNR=-3 dB以上的8PSK与QAM区分出来，平均识别正确率大于 98%。各节点性能的差异，由循环平稳特征阶数决定，识别性能随特征阶数升高而下降。

图2 各节点平均识别概率

实验 3 用本文方法与已有衰落信道识别方法进行比较。

先进行定性比较，表1是识别类型与预处理条件的比较结果。从对比结果看，识别信号类型上，累积量、循环累积量算法，可完成调幅、调相及幅相等线性调制的识别，无法完成调频，OFDM等非线性调制的区分；基于循环平稳检测算法，可实现调频、调相以及多载波信号的识别，无法完成调幅，QAM信号的类间识别。预处理要求上，本文算法无同步、已知参数要求，较已有方法低。

表1 各种衰落信道下调制识别算法比较

计算量上，当完成多种信号区分时，累积量、循环累积量识别特征为四阶或八阶[5]，本文的特征小于或等于四阶，阶数减小使特征计算量显著降低，已有方法预处理需频偏[5,9]或 SNR[1,3,4]估计，本文方法无参数估计与同步过程，因此总体计算量较已有方法降低。

再对识别性能进行定量比较，分别使用累积量、循环累积量及本文方法对衰落信道的 BPSK和4QAM 信号进行识别，1/Ts为 1500 baut(波特)，fe=50 Hz ，无定时误差，符号数1500,ρ为4。为了公平比较，均使用二阶特征，累积量：[1]，识别门限为 0.4；循环累积量：[5]，识别门限为0.4；本文算法使用的循环频率，检测门限Γ1=18.412, Γ2=19.807,从图3识别结果来看，循环平稳性检测算法性能要优于循环累积量与累积量算法。因为由于存在频偏，累积量算法未能满足适用条件，结果均为0.5(完全误判)；循环频率特征较循环累积量特征受衰落信道和噪声的影响小，因此在实验中，本文算法较其他方法识别效果更好。

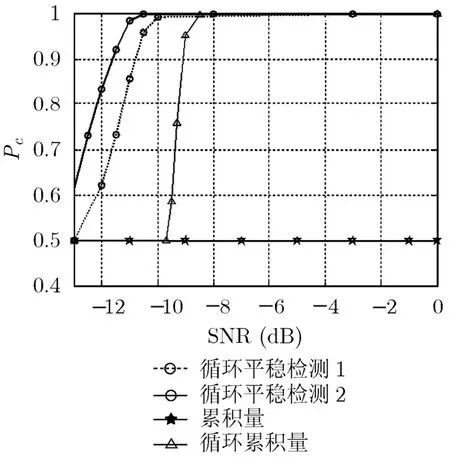
图3 不同算法平均识别概率

实验4 对信号参数与识别性能影响进行测试。使用特征3结合循环平稳性检测对BPSK进行识别。实验中1/Ts在[1000,1500] baut(波特)间随机变化，使用如下脉冲成型滤波器，方式1：矩形；方式2：根方升余弦 (系数0.25)；方式3：余弦 (系数0.5)。分别使用观测时间为 1 s, 0.5 s的样本，门限Γ=18.412，其他参数同仿真条件。从图4结果看：对于识别概率Pc(BPSK/BPSK)，除样本长度影响较大外，其他信号参数条件对算法影响较小。其原因由于循环平稳特征都是渐进估计量。实验表明在非频率选择性衰落信道下，算法具有一定的稳健性。

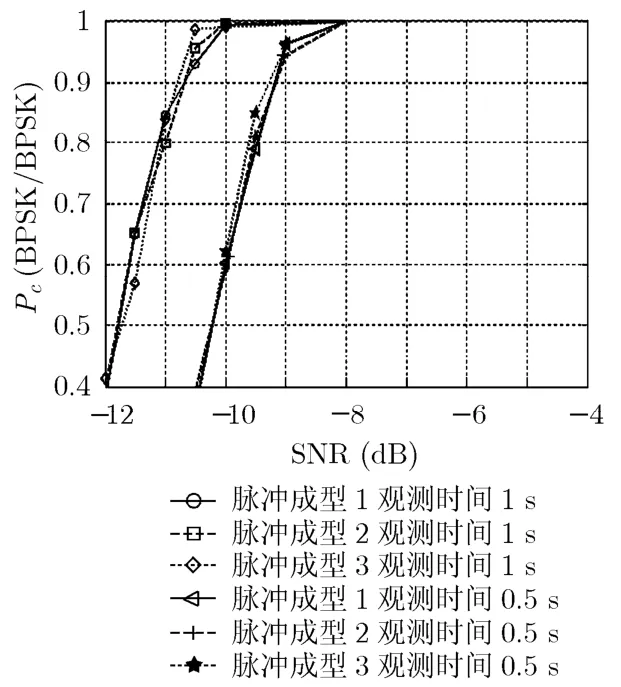
图4 不同调制参数下的BPSK识别概率

7 结束语

利用循环统计量的循环频率特征，与循环平稳性检测相结合，本文提出了一种适于多径信道盲接收条件的信号分类算法。较已有方法，该算法无需调制参数估计与同步等步骤，降低了对预处理的要求，在衰落信道低信噪比环境下，具有更理想的识别性能。算法有助于提升衰落信道盲接收条件下的信号识别能力。如何实现低预处理要求的 QAM 类间区分，应用SVM等先进分类器来提高识别效果等问题仍有待研究，以期进一步提升非合作盲接收下的信号分类能力，使算法应用于更广泛的场合。

参 考 文 献

[1] Wu H C, Saquib M, and Yun Z. Novel automatic modulation classification using cumulant features for communications via multipath channels.IEEE Transactions on Wireless Communications, 2008, 7(8): 3098-3105.

[2] Dobre O A, Abdi A, Ness Y B,et al.. Survey of automatic modulation classification techniques: classical approaches and new trends.IET Communications, 2007, 1(2): 137-156.

[3] Fahed Hameed, Dobre O A, and Popescu D C. On the likelihood-based approach to modulation classification.IEEE Transactions on Wireless Communications, 2009, 8(12):5884-5892.

[4] Orlic V D and Dukic M L. Automatic modulation classification algorithm using higher-order cumulants under real-world channel conditions.IEEE Communications Letters,2009, 13(12): 917-919.

[5] Dobre O A, Abdi A, Ness Y B,et al.. Cyclostationarity based modulation classification of linear digital modulations in flat fading channels.Wireless Personal Communications, 2010,DOI: 10.1007/s11277-009-9776-2.

[6] Like E, Chakravarthy V D, Ratazzi P,et al.. Signal classification in fading channels using cyclic spectral analysis.EURASIP Journal on Wireless Communications and Networking, 2009, DOI: 10.1155 /2009/879812.

[7] Gardner W A, Napolitano A, and Paura L. Cyclostationarity:half a century of research.Signal Processing, 2006, 86(4):639-697.

[8] Dobre O A,et al.. Joint signal detection and classification based on first-Order cyclostationarity for cognitive radios.EURASIP Journal on Advances in Signal Processing, 2009,DOI:10.1155/2009/656719.

[9] Dobre O A, Ness Y B, and Su W. Higher order cyclic cumulants for high order modulation classification. IEEE Military Communications Conference, Boston, USA, 2003:112-127.

[10] Punchihewa A, Zhang Q, Dobre O A,et al.. On the cyclostationarity of OFDM and single carrier linearly digitally modulated signals in time dispersive channels:theoretical developments and application.IEEE Transactions on Wireless Communications, 2010, 9(8): 2588-2599.

[11] Dandawate A V and Giannakis G B. Statistical tests for presence of cyclostationarity.IEEE Transactions on Signal Processing, 1994, 42(9): 2355-2369.