单路反馈射频功放预失真线性化方法

詹 鹏 秦开宇 蔡顺燕

①(电子科技大学空天科学技术研究院 成都 611731)

②(西华师范大学物理与电子信息学院 南充 637002)

1 引言

功率放大器是通信系统的重要组成部分，非线性是其固有的特性，功放的非线性会导致输出信号频谱扩展，从而对邻近信道产生干扰，使通信系统误码率增大。而新兴的调制方式具有非恒定包络、宽频带及高峰平比等特点，这些特点决定了必须采用高线性度的功放。为此，人们提出了许多功放线性化方法，常用的有功率回退、前馈、负反馈、预失真等。其中，数字预失真技术具有稳定、高效、宽带宽与自适应等优势，能达到中等程度的线性化，是比较有前途的一种线性化技术[1,2]。

在窄带功放系统中，可以不考虑功放的记忆效应，但在宽带功放系统中，功放的记忆效应不容忽略。常用的带记忆的非线性模型有Volterra级数模型[3,4]，Wiener模型，Hammerstein模型，记忆多项式模型[5−7]等，其中记忆多项式模型以其形式简洁、易在硬件上实现而得到了广泛的应用。

文中对记忆多项式模型进行理论推导证明：经非线性失真后IQ两路信号中的任何一个分量(同相或正交分量)都包含了完整的非线性失真信息。基于该原理，本文提出一种采用单路反馈的预失真线性化方法，只需要对IQ两路信号中的一路进行自适应处理就能间接地获取预失真器的参数。采用该方法可省去一路反馈采样电路，从而也就省去了对一路高速数据流的处理，降低了系统硬件成本及复杂度，且该方法还能消除使用正交解调器所带来的增益和相位不平衡问题[8]，可进一步提高预失真的线性化性能。

2 预失真结构及非线性系统模型

数字预失真的基本原理是在信号进入功放前对信号进行预处理，且预处理器的非线性特性与功放的非线性特性相逆，从而消除功放非线性的影响，使整个功放系统表现出线性特性。为了得到功放的非线性逆模型，常采用图1所示的直接逆间接学习结构[9,10]，该学习结构根据输入到功放前和从功放反馈回来的信号，采用后失真的方法直接得到非线性功放的逆模型，并将该逆模型的参数作为预失真器的参数。

图1 直接逆间接学习结构系统框图

Volterra级数模型能够很好地描述带记忆的非线性系统，但是随着模型阶数的增加，其计算量急剧增加，影响了该模型在工程实际中的应用，为此人们提出了一些简化的带记忆的非线性模型，其中，记忆多项式模型应用较广，其表达式如下：

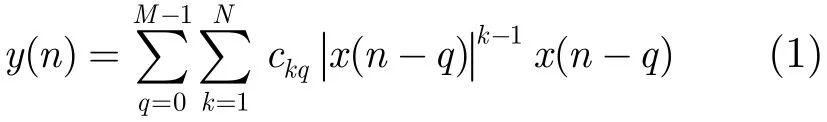
其中N为记忆多项式的最高阶次，M为记忆深度，ckq为记忆多项式的复系数，表示对复信号x(n−q)求模。在工程实际应用中，功放的非线性模型可以去掉偶次的非线性失真项，因为预失真系统的反馈回路中通常加有滤波器，偶次项的失真信息在反馈回路中已被滤除掉，如果把功放系统和反馈系统看作一个整体的非线性系统，则该系统不包括偶次项的非线性失真，所以，为了进一步简化模型，降低计算复杂度，功放的记忆多项式模型可只使用其中的奇次项。

3 单路反馈预失真线性化方法

在数字基带预失真系统中，为了获得预失真器的模型参数，通常需要将反馈回的IQ两路信号都进行采样(如图1所示)，而实际上利用其中的一个分量就可获得预失真器的模型参数，下面将证明这个结论。将式(1)中同一个记忆深度的项合并在一起可得

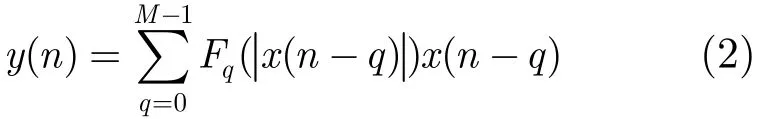
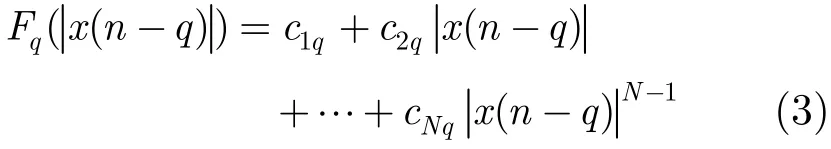
设式(3)中的复系数ckq=akq+jbkq，其中akq和bkq分别为ckq的实部和虚部，将式(3)按照实部和虚部分开可得

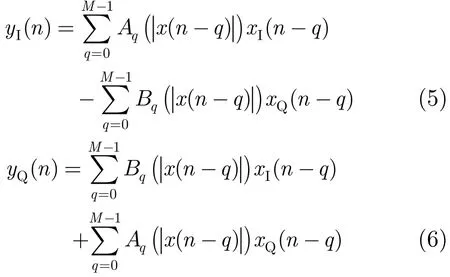
从式(2)，式(4)可以看出，只要得到了各个多项式 Αq(·)和 Βq(·)的系数(其中q=0,1,…,M−1)，就可求出待识别的记忆多项式模型参数，而从式(5)，式(6)可以看出，输出的复信号y(n)的 IQ两个分量都与 Αq(·)和 Βq(·)有关。也即，非线性变换特性在失真后输出的IQ两路信号中都体现了出来，对其中任何一路失真信号进行非线性参数的识别，就能间接得到整个非线性系统的模型参数。所以，只需取其中一路反馈信号，采用自适应算法识别出多项式 Αq(·)和 Βq(·)的系数，就可间接得到记忆多项式模型的参数。

基于以上结论，本文提出一种基于单路反馈的预失真线性化方法，其结构框图如图2所示。与图1中直接逆间接学习结构不同的是：由于只需使用一路反馈信号，故可用混频器代替正交解调器，相应地也只有一路反馈采样电路。该方法首先对功放非线性系统模型进行识别，然后再求出预失真器的模型参数。

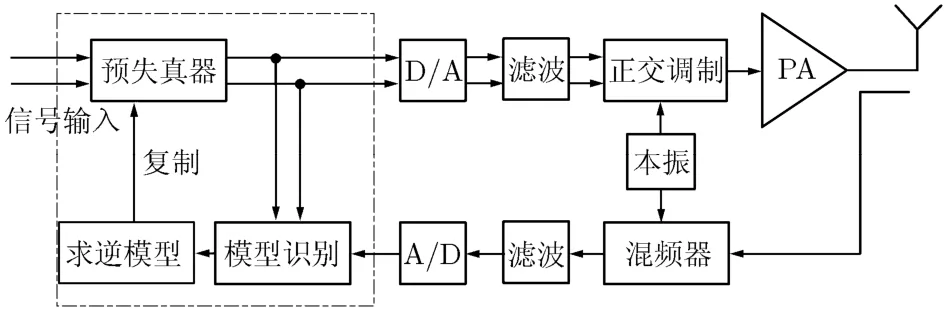
图2 单路反馈预失真结构框图

在常用的直接逆间接学习结构中(见图1)，反馈回路采用的是正交解调器，而正交解调器通常存在增益和相位不平衡失真(IQ不平衡失真)，该失真会在一定程度上降低预失真线性化的性能。为此文献[11]提出了针对IQ不平衡失真的数字补偿方法，然而，数字补偿会在一定程度上增加系统的复杂度，并且数字补偿的改善程度也是有限的。本文提出的单路反馈预失真方法由于只需要使用一路反馈信号，所以不存在IQ不平衡失真的问题，而且还可省去一路反馈采样电路，在降低成本、简化设计的同时还能提高预失真线性化的性能。

4 算法及仿真分析

基于上文提出的单路反馈预失真线性化方法，首先需要识别出功放的非线性失真模型参数。在这里，预失真器模型和功放失真模型都采用记忆多项式模型，假设取I路反馈信号，并设r(n−q)=|x(n−q)|，I路输出信号由式(4)，式(5)可简写成向量相乘的形式

为验证文中提出方法的正确性，在 MATLAB中进行了仿真，采用只含奇次项的记忆多项式作为功放失真模型，其模型参数见参考文献[5]，采用16QAM信号作为测试信号。仿真实验包括：本文提出的单路反馈预失真(反馈回的 IQ 信号只需要一路)、无IQ不平衡失真时的普通预失真(采用图1的学习结构，且反馈回的IQ两路信号都需要)、存在IQ 不平衡失真时的普通预失真和文献[11]提出的有IQ补偿的预失真。其中，IQ不平衡失真的增益和相位误差分别设为5%和5º。仿真结果如图3所示(曲线(c)(d)(e)几乎重叠)。

图3 预失真前后功率谱对比图

从仿真结果可以看出，当不存在IQ不平衡失真时，本文提出的预失真方法能够达到与采用普通预失真时相当的线性化性能，都能有效抑制带外频谱扩展。而当存在IQ不平衡失真时，采用普通预失真方法的带外失真增大，说明普通预失真方法会受到IQ 不平衡失真的影响，此外，采用文献[11]提出的有IQ补偿的预失真也能达到很好的预失真效果，与本文提出的单路反馈预失真的线性化性能相当。

为了评价采用不同预失真方法时的带内失真情况，对误比特率(BER)进行了仿真，从图4的仿真结果可以看出，当存在IQ不平衡失真时，采用普通预失真时的误码率较高。而单路反馈预失真、无IQ失真时的普通预失真、以及文献[11]提出的有IQ补偿的预失真的误码率相当，且与理想高斯信道的性能比较接近。

图4 误比特率仿真图

以上仿真结果表明：当不存在 IQ不平衡失真时，普通预失真方法与单路反馈预失真方法的线性化性能相当，都能达到很好的线性化效果；而当存在IQ不平衡失真时，采用普通预失真方法的线性化性能降低，而本文提出的单路反馈预失真可以消除IQ 不平衡失真的影响,该方法和文献[11]提出的有IQ补偿的预失真都能够达到比较好的预失真线性化效果。

5 物理实验验证

为验证本文提出的单路反馈预失真方法的正确性，搭建了基于仪器的物理实验验证平台。实验采用16 QAM信号作为测试信号，预失真器采用只含奇次项的 7阶记忆多项式模型，其记忆深度为 3。当反馈信号无IQ不平衡失真时，采用不同方法所得的实验结果如图5所示。从图中可以看出，与未加预失真的情况相比，采用普通的预失真(用图1中的直接逆间接学习结构，其反馈回的IQ两路信号都需要)和本文提出的单路反馈预失真都能达到比较满意的线性化效果，带外频谱扩展被抑制了10 dB以上。且采用本文提出的预失真方法比普通的预失真方法的带外失真略小，其原因是使用仪器获得的正交解调信号存在残留的IQ不平衡失真，而本文提出的预失真方法可以消除IQ不平衡失真的影响，故其预失真效果比采用普通的预失真方法略好。

图5 无IQ不平衡失真时预失真前后对比图

为验证本文提出的预失真方法在消除 IQ不平衡失真方面的优势，我们给反馈信号人为地加入了IQ不平衡失真(增益和相位不平衡误差分别为3%和3º)。采用普通的预失真、文献[11]提出的有IQ补偿的预失真、以及本文提出的单路反馈预失真所得的实验结果如图6所示。从图中可以看出，IQ不平衡失真会使普通预失真方法的线性化性能降低，采用文献[11]提出的有IQ补偿的预失真能降低IQ不平衡失真所带来的影响，但是数字补偿方法的补偿能力是有限的，IQ不平衡失真无法被完全补偿。而本文提出的单路反馈预失真方法可以消除 IQ不平衡失真的影响，其实验所得的带外失真最小。

图6 有IQ不平衡失真时不同预失真方法对比图

为评价信号的带内失真情况，对采用不同预失真方法时输出的 16 QAM 信号的误差向量幅度(EVM)进行了测量，测量结果如表1所示。从表1可以看出，当存在IQ不平衡失真时(增益和相位不平衡误差分别为3%和3º)，采用普通预失真方法的带内失真最大，采用文献[11]提出的有IQ补偿的预失真方法能够降低IQ不平衡失真的影响，其EVM值有一定程度的降低。而本文提出的单路反馈预失真和无 IQ不平衡失真时的普通预失真拥有最小的EVM 值(本文提出的预失真方法的EVM值更小，其原因是使用仪器得到的解调信号中存在残留的IQ 不平衡失真)，这说明本文提出的预失真方法能够有效消除IQ不平衡失真的影响。

表1 EVM值测量结果对比

从以上物理实验结果可以看出，本文提出的单路反馈预失真方法是正确和可行的，该方法能有效消除正交解调器IQ不平衡失真的影响，其线性化性能与无IQ不平衡失真时的普通预失真方法相当，且优于有IQ补偿的预失真方法。

6 结论

本文经过理论推导证明：功放的非线性失真特性在反馈并解调后的IQ两路信号中都体现了出来，对任何一路信号进行参数识别就能间接的得到整个非线性系统的模型参数。基于该原理，本文提出一种基于单路反馈的预失真线性化方法，首先用单路反馈原理识别出功放的非线性模型，然后再求预失真器的模型参数。仿真和物理实验都证明了单路反馈预失真方法的正确性和可行性，且其性能优于采用有IQ补偿的预失真方法，该方法不仅可以消除使用正交解调器所带来的IQ不平衡失真，而且还可省去一路反馈采样电路，从而可省去对一路高速数据流的处理，在降低成本、简化设计的同时还能提高预失真的线性化性能。

[1] Rawat M, Rawat K, and Ghannouchi F M. Adaptive digital predistortion of wireless power amplifiers/transmitters using dynamic real-valued focused time-delay line neural networks[J].IEEE Transactions on Microwave Theory and Techniques,2010, 58(1): 95-104.

[2] Mehta J, Zoicas V, Eliezer O,et al.. An efficient linearization scheme for a digital polar EDGE transmitter[J]IEEE Transactions on Circuits and Systems II:Express Briefs, 2010,57(3): 193-197.

[3] Abd-Elrady E, Li G, and Kubin G. Distortion compensation of nonlinear systems based on indirect learning architecture[C]. 20083rd International Symposium on Communications,Control, and Signal Processing, St. Julians, Malta, 2008:184-187.

[4] 南敬昌, 刘元安, 李新春, 等. 记忆效应非线性功放展Volterra模型分析与构建[J]. 电子与信息学报, 2008, 30(8):2021-2024.Nan Jing-chang, Liu Yuan-an, Li Xin-chun,et al.. Analysis and modeling on expanding Volterra-series behavior model for nonlinear power amplifier with memory effects[J].Journal of Electronics&Information Technology, 2008, 30(8):2021-2024.

[5] Ding L, Zhou G T, Morgan D R,et al.. A robust digital baseband predistorter constructed using memory polynomials [J].IEEE Transactions on Communications,2004, 52(1): 159-165.

[6] 王华东, 何松柏, 鲍景富. 一种基于互相关序列的功放行为模型建立方法[J]. 电子与信息学报, 2009, 31(5): 1201-1204.Wang Hua-dong, He Song-bai, and Bao Jing-fu. A method of PA behavioral modeling based on cross-correlation sequence[J].Journal of Electronics&Information Technology, 2009, 31(5): 1201-1204.

[7] 李波, 葛建华, 王勇. 一种新的分数阶记忆多项式预失真器[J].电子与信息学报, 2009, 31(8): 1961-1964.Li Bo, Ge Jian-hua, and Wang Yong. A novel fractional order memory polynomial predistorter [J].Journal of Electronics &Information Technology, 2009, 31(8): 1961-1964.

[8] Teikari I, Vankka J, and Halonen K. Baseband digital predistorter with quadrature error correction [J].Analog Integrated Circuits and Signal Processing, 2006, 46(1): 73-85.

[9] Ding L, Ma Z X, Morgan D R,et al.. A least-squares newton method for digital predistortion of wideband signals [J].IEEE Transactions on Communications, 2006, 54(5):833-840.

[10] Anttila L, Handel P, and Valkama M. Joint mitigation of power amplifier and I/Q modulator impairments in broadband direct-conversion transmitters[J].IEEE Transactions on Microwave Theory and Techniques, 2010,58(4): 730-739.

[11] Young-Doo K, Eui-Rim J, and Lee Y H. Adaptive compensation for power amplifier nonlinearity in the presence of quadrature modulation/demodulation errors[J].IEEE Transactions on Signal Processing, 2007, 55(9): 4717-4721.