一种基于MATLAB及FPGA的FIR低通滤波器的设计与实现

阿依夏木·力提甫，赵惠昌，王丹琦

（1．新疆师范大学 物理与电子工程学院，新疆 乌鲁木齐 830054；2．南京理工大学 电光学院，江苏 南京 210094）

随着信息技术的发展，数字电路的设计逐步摆脱传统的设计模式，越来越多的数字信号处理系统开始使用可编程门阵列和硬件描述语言实现。现场可编程门阵列（FPGA）是一种可以重复改变组态的电路，特别适合产品发展时需要不断变更设计的应用，有效节省产品上市的时间。FPGA的修正不需要变更硬体，仅仅需要更改软体即可。这大大节省研发的成本，而且仅需要下载新的程式码便可以达到产品上市后的升级功能。 现在FPGA技术已经成为多种数字信号处理应用的强有力的工具。与通用DSP相比，FPGA器件能够以高速，实时，低成本，高灵活性的优点应用于数字信号处理领域，利用FPGA实现数字信号处理成为数字信号处理领域的一种新的趋势，它可以完全取代通用DSP芯片或作为通用DSP芯片的协处理器进行工作。低通滤波器的设计方面国内外提出了不少理论方案，但是具体实现过程很少有提及。本文灵活使用MATLAB语言和QuartusII软件设计出了一种高效低通滤波器，填充了低通滤波器从理论到实际设计过程的一片空白。

1 滤波器的MATLAB设计

数字滤波技术作为数字信号处理的基本分支之一，就是提取信号的有用分量，削弱无用分量的技术，被广泛应用于数据处理，图像处理、雷达、声纳信号处理、地址石油勘探等很多领域，越来越受到人们的关注。由单位冲击响应的不同数字滤波器有两种类型：有限冲击响应 （Finite Impulse Response，FIR）数字滤波器和无限冲击响应（Infinite Impulse Response，IIR）数字滤波器。两种类型滤波器相比而言，对于同样的滤波器设计指标，虽然FIR滤波器成本较高，信号延迟较大并且FIR滤波器没有现成的计算公式（必须要用计算机辅助设计软件（如MATLAB）来计算），但是FIR滤波器可以采用FFT算法，运算速度较快；精度高，具有严格的线性相位等特点优于IIR数字滤波器已被广泛应用。下面重点介绍FIR数字滤波器的基础上，基于MATLAB及FPGA实现一种优化的FIR低通滤波器。

1.1 FIR数字滤波器的设计方案

FIR数字滤波器是一个线性时不变系统（LTI），N阶因果有限冲激响应滤波器可以用差分方程：

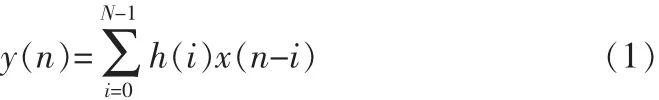
来描述，其中 y（n）是滤波器的输出信号，x（n）是滤波器的输入信号，h（n）是滤波器系数。从以上的表达式可以看出来，FIR滤波器是通过加法器，乘法器和移位器组合而实现的。加法器和乘法器的数量，速度和效率等特性对于滤波器的性能非常重要。

在很多应用场合，滤波器都是线性时不变滤波器，也就是带有常系数的滤波器。具有线性相位的FIR滤波器的系数具有中心对称特性，即 h（i）=±h（N-1-i）。 则其输出表达式（1）可以编写成如下形式：

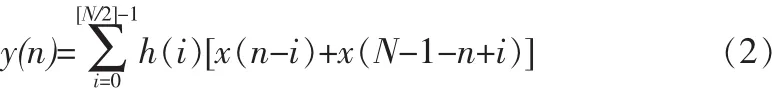
由此可见，利用它的对称形式比直接实现少用了一倍的乘法器，大大节省了硬件资源，而且可以提高速度[1]。

1.2 参数提取

设计指标如下：

类型：低通滤波器；Beta 值=0．5；采样频率：FS=80 kHz；窗函数：Kaiser窗；截止频率：FC=10 kHz；阶数：15 阶；数据宽度：输入10位，输出10位。

本次设计选择了Matlab2009的Toolboxes（数字信号处理工具箱）中的 FDATool（Filter Design ＆ Analysis Tool）工具来设计滤波器，使设计过程更加简洁，精确[2]。FDATool是一个功能强大的数字滤波分析设计工具，它涵盖了信号处理工具箱中所有的滤波器设计方法。利用它可以设计出满足各种性能指标的滤波器，并可查看该滤波器的各种分析图形。待滤波器设计满意后，还可以把其系数直接导出为MATLAB变量，文本文件或C语言头文件等[3]。

打开Matlab软件主窗口，在Workspace上输入语句：FDATool，将出现数字信号处理工具窗口，窗口输入相应的参数以后可以形成符合要求的低通滤波器系数。低通滤波器系数通过在Matlab主窗口上输入

round（Coefficient*（2^11））命令被放大 2 048 倍后得到如下系数：

Coefficient=[-31 -88 -106 -54 70 239 401 499 499 401 239 70-54-106-88-31]

根据以上滤波器系数设计，可以得到该滤波器模型的差分方程如下：

y（n）=h（0）x（n）+h（1）x（n-1）+h（2）x（n-2）+…，…h（n-1）x（1）+h（n）x（0）=-{-31[x（n）+x（n-15）]+88[x（n-1）+x（n-14）]+106[x（n-2）+x（n-13）]+54[x（n-3）+x（n-12）]}+70[x（n-4）+x（n-11）]+239[x（n-5）+x（n-10）]+401[x（n-6）+x（n-9）]+499[x（n-7）+x（n-8）]

1.3 FIR滤波器的实现原理

根据以上所说的滤波器设计思路，可以将FIR滤波器的原理图画出来，如图1所示。

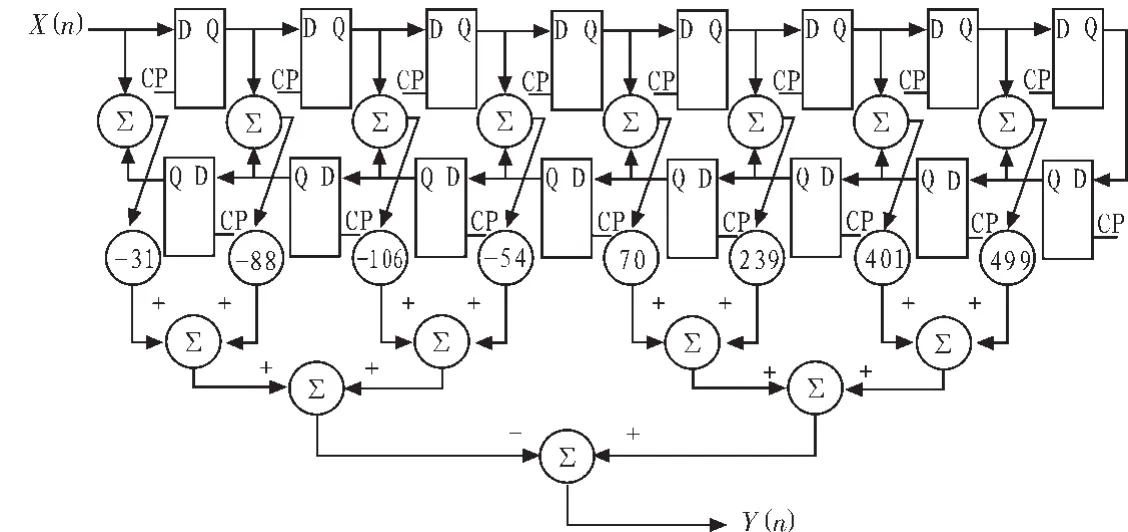
图1 FIR滤波器原理框图Fig．1 Block diagram of the FIR filter

从以上滤波器原理框图可以看出来，设计的FIR滤波器由16个小BDF文件和一个总体BDF文件组成，小BDF文件分为以下4种模块：寄存器、加法器、减法器、乘法器。下面结合本设计分别介绍每一个模块。

2 滤波器的FPGA实现

2.1 寄存器模块的实现

寄存器用于寄存一组二值代码，对寄存器的触发器只要求它们具有置1、置0的功能即可，因而本设计中用D触发器组成寄存器，实现寄存功能。寄存器要求实现的功能为在CP正跳沿前接收输入信号，正跳沿时触发翻转，正跳沿后输入即被封锁。本次设计要求输入数据宽度为10位，总共需要16个十位寄存器。系统生成的寄存器模块如图2所示，十位寄存器用VHDL语言描述如下：

图2 10位寄存器模块Fig．2 Module of 10 bit register

2.2 乘法器模块的实现

众所周知，二进制数在实现乘法或加法时，数值为0的位是不参与运算的。因此，对输入信号进行编码时，如果能使0位的数量最多，则完成相应的运算所需要的硬件将会大大减少，运算的速度也会相应地提高很多。正则有符号数字量（Canonic signed digi，t简称CSD）正是基于此思想而提出来的一种新型编码方法，它是具有最少非0元素的表示法[4]。

从资源和速度考虑，常系数乘法运算可用CSD算法，将常系数分解成几个2的幂的和形式，通过每一个分解因数的移位相加来实现乘法运算。对于本次设计分析各个乘法器的系数，实现输入带符号数据与固定数据两个二进制数的乘法运算 ，比如31=32-1=2^5-2^0，分别左移5位和 0位；88=64+16+8=2^6+2^4+2^3，分别左移6位，4位和3位等。以此类推，乘法器其他系数按同样的方法分解成2的幂的和形式。下面以乘70乘法器的VHDL语言来描述以上算法，70=64+8-2=2^6+2^3-2^1，分别左移6位，3位和一位；

运行此程序可以得到验证波形，如图3所示。通过此仿真波形可以验证程序的正确性。程序运行成功之后，打开File菜单栏的CreateUpdate选项，选择Create Symbol File for Current File命令，系统自动生成当前程序的模块，并以bsf文件的形式保存在制定文件夹，如图4所示。

图3 实现乘70的乘法器仿真波形Fig．3 Simulation waveform ofmultiplying unitby 70 times

图4 乘70的乘法器模块Fig．4 Module ofmultiplying unit by 70 times

其他乘法器模块按同样的方法生成，保存到同一个文件夹。

2.3 加法器模块的实现

整个系统需要三级加法器：第一级加法器只需要输入10位输出11位的加法运算。第二级加法器包括4个加法器，需要考虑乘法器输入输出数据的位数。本次试验用的乘法器都是专用乘法器，不同乘法器输出的信号位数也不一样。因此第二次使用加法器时需要设计4种专用加法器把从各个乘法器输出的信号位数统一起来。

1）对于乘31和乘88乘法器需要设计17位数加18位数生成22位数的加法器；

2）对于乘106和乘54乘法器需要设计18位数加18位数生成22位数的加法器；

3）对于乘70和乘239乘法器需要设计18位数加20位数生成22位数的加法器；

4）对于乘401和乘499乘法器需要设计20位数加21位数生成22位数的加法器。

第三级加法器需要两个能实现22位加22位生成23位数的加法器。以上几种加法器用VHDL语言描述的思路是一样的，现举一个为例说明加法器的实现原理。

对于乘70和乘239乘法器需要设计18位数加20位数生成22位数的加法器，加法思路是位数少的被加数补最高位，生成位数高的加数。系统生成的18位数加20位数生成22位数的加法器的模块如图5所示。加法器部分程序如下：

图5 加法器模块Fig．5 Module of adder

减法器的原理与加法器类似，并行式减法器与加法器的区别仅仅在于最后的和数为两数相减。

3 高效FIR滤波器的FPGA实现

根据以上思路，采用Altera公司的Quartuas II开发软件对此FIR滤波器进行设计及仿真[5-6]。FIR滤波器的电路连接与其原理图连接方式类似，首先打开Quartuas II软件点击Block Diagram/Schematic文件，新建一个bdf文件，然后调用生成的寄存器，各种加法器以及乘法器模块，按照如图1所示的原理图前后连接可以形成FPGA滤波器整体电路，利用该软件所提供的Waveform Editor进行时序仿真可以得到时序仿真波形。

时序仿真需要一系列输入信号，为了验证方便利用matlab在正弦函数上取特定信噪比的几个点作为输入序列，本次设计选取的信噪比为20分贝，此函数为：

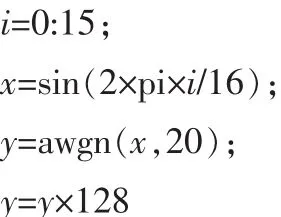
输出结果：y=[14，63 ，79，119，112 ，104，90，69，-10 ，-44，-93 ，-104， -142，-118，-83 ，-35]， 此序列代表信噪比为 20分贝的正弦信号序列，把这些序列作为以上系统的输入信号运行，结果如图6所示，图上clk是控制输入的时钟信号，时钟频率为100 MHz，clear是加法器及锁存器的清零信号，低电平0有效，Din是外部的输入信号，Dout是最终的外部输出信号。

理论上，以上序列y的值与滤波器系数求卷积，可得滤波器理想输出值 conv（x，y）：

conv （x，y） ={1．97， 5．22， 12．67， 15．12， 15．61， 13．75，9．56，3．59，-3．17，-9．50，-14．16，-16．28，-15．64，-12．7，-8．48，-4．23}

通过matlab软件可以画出以上两种数据Dout和conv（x，y）对应的图形，分别如图 7（a）和（b）所示。

图6 FIR滤波器仿真波形Fig．6 Simulation waveform of Finite Impulse Response digital filter

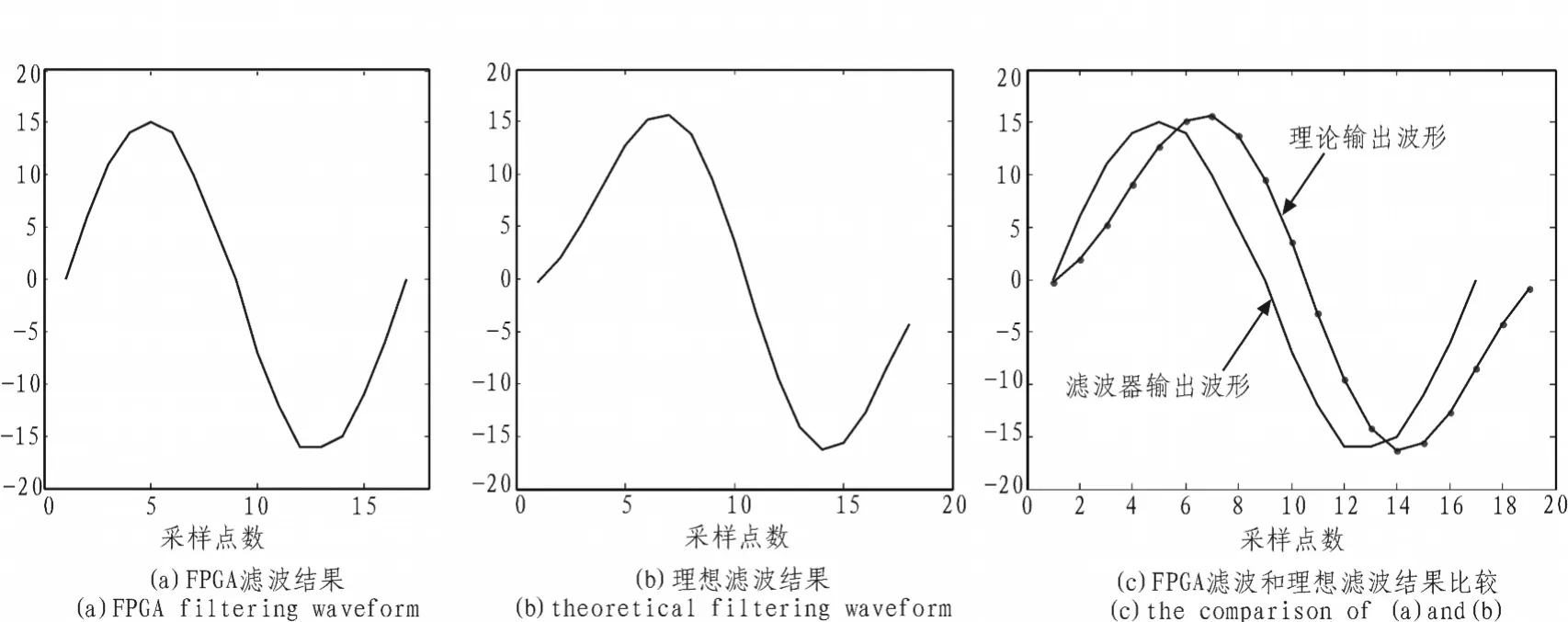
图7 FPGA仿真滤波结果与理想FIR滤波结果对比图Fig．7 The comparison of FPGA filtering and theoretical filtering

从以上数据和波形可以看出理论值除个别点数外，波形基本没有毛刺。图中横坐标是采样点数，纵坐标代表的是采用10位二进制数量化后的幅值，图中的实线是FPGA滤波结果，带固定点的实线是滤波器理论值。从图7可以看出，用本文提出的设计方案实现的基于FPGA芯片和MATLAB软件的FIR滤波器的滤波结果与理想滤波结果是非常接近的，对比图中FPGA滤波结果比理想值稍低，原因是由于在FPGA滤波器实现的过程中，为了节省硬件资源，将数据做了截掉低6位的处理，从而产生了一点误差。但是，从仿真结果来看，该截掉低位的处理并不影响滤波器的性能。这次设计采用的是输入信号信噪比等于20 db时的情况，使用过程中根据实际设计要求可以更改信噪比，随着信噪比的降低输出信号的恢复程度有所降低，一般按这种方法设计出来的低通滤波器最高可以恢复信噪比为-20 db的输入信号。

4 结 论

FIR滤波器在数字信号处理的各个领域中起着很重要的作用，其性能优劣对信号处理的结果有举足轻重的影响。该文采用对称结构、被加法和移位代替的乘法运算、优化的CSD编码、流水线技术、级联技术等几个方面，对传统的FIR滤波器的设计方法进行了改进，并借助Altera公司的FPGA芯片和QuartusII软件以及Matlab软件对设计方案进行了仿真验证。仿真实验结果表明，该FIR滤波器的实现方案，具有工作速度快、实时信号好、节省硬件资源等特点，能够满足实际的数字系统的要求。

[1]李亚奇，张雅绮．线牲相位FIR数字滤波器[J]．电子测量技术， 2005（6）：35-36．

LI Ya-qi ，ZHANG Ya-qi．The design of a linear phase FIR digital filter[J]．Electronic Measurement Technology．2005（6）：35-36．

[2]王宏．MATLAB6．5及其在信号处理中的应用[M]．北京：清华大学出版社，2004，231-251．

[3]梁静．数字FIR滤波器的MATLAB设计和仿真[J]．现代机械，2003（6）：88-91．

LIANG Jing．The design and imitate of digital FIR filter by MATLAB[J]．Modern Machinery．2003（6）：88-91．

[4]Uwe Meyer-Baese．数字信号处理的FPGA实现[M]．刘凌，胡永生，译．北京：清华大学出版社，2003．

[5]张驰，郭黎利，孙岩．基于MATLAB及FPGA的高速FIR滤波器的设计[J]．信息技术， 2006（7）：31．

ZHANG Chi， GUO Li-li， SUN Yan．A high speed FIR filter design based on MATLAB and FPGA device[J]．Information Technology， 2006（7）：31．

[6]蒋立平，谭雪琴，王建新．一种基于FPGA的高效FIR滤波器的设计与实现[J]．南京理工大学学报，2007（2）：125-128．

JIANG Li-ping， TAN Xue-qin， WANG Jian-xin．Design and implementation of efficient FIR filter based on FPGA[J]．Journal of Nanjing University of Science and Technology．2007（2）：125-128．