一种基于社团结构的CPS节点协同感知方法

周有为，杨 强

（国防科学技术大学 信息系统工程重点实验室，湖南 长沙 410073）

CPS综合了传感系统、通信系统、计算系统和控制系统，目的在于更广泛的互联互通、更透彻的认知物理世界、更有效的控制物理世界，使信息世界与物理世界紧密融合，实现对物理世界安全、可靠、高效、实时、协同的感知和控制[1]。传感系统实现对物理世界的直接感知，通过通信系统将感知的信息传递给CPS计算系统和控制系统，实现对物理世界的控制和决策。感知是CPS的基础，感知的正确性和有效性是CPS实现正确控制的前提。大多数情况下，CPS中的节点数目量级较大，单个节点的感知能力有限，感知的数据存在不确定性，因此需要CPS节点之间协同感知。CPS中节点之间可能是完全对等的，也可能存在中心节点来协同网络中的节点。中心节点的计算能力较强，负责控制，管理，协同一定区域内的节点。CPS中协同感知是指节点不仅要知道自己的状态，还要了解一定邻域范围内其余节点的状态，多节点协同，共同完成一项任务，这样可以有效提升CPS感知的正确性和可靠性。

目前在事件监测中表现出较为稳定性能的方法有两种，Jiang[2]等提出了一种使用R树结构来监测感知网络中的事件。Fan[3]等提出了一种名为ToD的方法，这种方法使用动态转发技术监测事件是否发生。Jiang给出的R树方法需要感知节点知道事件区域的形状，Fan提出的动态转发方法需要事先知道事件位置，同时事件要有已知区域上限[4]。

本文利用复杂网络中的社团结构划分划分算法和观点动力学中的多数投票者模型，给出一种新的思路来求解感知网络中节点对事件状态的判断。

1 CPS协同感知问题

我们主要考虑存在中心节点的CPS感知网络，中心节点自身的通信能力、计算能力比网络中其他节点强。首先不考虑中心节点自身的能耗，主要研究在节点网络拓扑（即节点的部署位置）确定的情况下选取哪些节点作为中心节点，中心节点如何协同区域的其他节点，使所有节点形成对事件M的一致判断。

在一个区域S部署了N个节点，这N个节点是密集部署的，N个节点协同感知一个事件M，节点感知的物理信息为F，每个节点有一个敏感区间[ai，bi]（i=1，2，…，N），当节点 i感知的信息fi∈[ai，bi]时，节点i判定事件 M发生，节点i对事件 M的感知状态值更新为1（我们假定节点对事件E的感知状态默认值为0）。单个节点感知信息的可靠度和准确性有限，如何选取中心节点，中心节点如何协同区域中的其他节点，最后形成所有节点对事件M感知状态的判断是我们求解的问题。

2 基于社团结构的协同感知策略

CPS中单个节点的感知能力，计算能力和通信能力都是有限的，每个节点只能和其邻域的节点进行通信，N个节点可以抽象为一个网络G（V，E），V表示网络的节点，E表示网络中的边。在我们描述的问题中，V代表节点，E代表能够相互通信的节点之间的链路，我们可以用复杂网络以及观点动力学中的相关理论来研究CPS中节点的协同感知问题。算法的过程如下：

1）CPS节点网络社团划分 首先选取中心节点位置。在CPS节点感知网络中，节点的数量级较大，可以将CPS节点网络抽象为一个复杂网络，网络的顶点表示节点的位置，网络中的边连接能够直接通信的节点。利用复杂网络的社团结构分析算法对CPS节点网络进行社团划分，CPS感知网络的节点数量级通常很高，因此需要选取适当的社团划分算法。Newman提出的凝聚算法[5]分析的节点数量可以达到百万个，对于CPS感知网络来说，这种算法较为适用。

凝聚算法通过模块性来衡量网络质量的划分[6]。若一种社团划分的算法将网络划分为k个社团。定义一个k阶方阵E=（eij），其中元素eij表示网络中连接两个不同社团的节点的边在所有边中所占的比例，这两个节点分别位于第i个社团和第j个社团[7]矩阵E中主对角线上各元素之和为每行各元素之和为模块性的定义为：

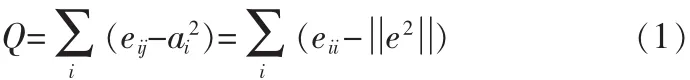
①将每个节点独立的看作一个社团，这样在初始条件下网络中一共有n个社团。。

②依次合并有边相连的社团对，按照式（2）计算合并后的Q值增量，每次合并沿着使Q增大或者减小的方向进行。

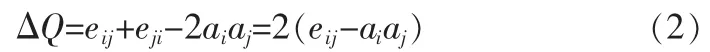
③重复第②步，不断合并社团，直到整个网络都合并成为一个社团。这个过程最多执行n-1次。

以上步骤完成后能够得到一个社团结构分解的树状图。在不同位置断开就可以得到不同的社团结构。在这些社团结构中，选取局部最大的Q值，就可以得到最好的社团结构[7]。

当网络的社团划分结束后，分别考虑每个社团内部的网络结构，建立每个社团网络节点间的距离矩阵Dij。Dij中的元素dij表示节点i和节点j的最短路径。距离矩阵每i行的和n为 表示节点i与社团内部其余所有节点最短路径的距｝离总和，其中n为网络节点的数目。求解（i=1，2，…，n），选取距离总和最小的节点作为社团的中心节点，中心节点负责协同社团内部的节点。

当网络完成第一次社团划分后，我们可以将网络的中心节点再次抽象成一个复杂网络，再次进行社团划分，选取第二级的中心节点，这个过程可以迭代下去，定义迭代重数k，根据网络规模的实际大小确定迭代的次数，从而实现对网络的分层控制。

2）社团内部的节点协同 每个中心节点负责处理社团内部节点的感知信息，社团内部的协同可以采用常用的观点动力学模型，例如投票者模型，多数决定模型等。根据应用的不同选取适当的模型，社团内部节点的感知信息汇集到中心节点，每个中心节点处理该社团内的感知信息，然后网络中所有中心节点再次进行协同，中心节点的协同也可以采用观点动力学中的模型，最后实现CPS感知网络的协同。社团内部节点的协同过程为：CPS系统中的节点感知一种特定的物理信息F，定义区间[a，b]为节点对F的敏感区间。当节点感知的信息f∈[a，b]时，感知节点判断事件E被触发，节点对应的值更新为1，否则节点的值保持为0，由于单个节点的感知存在不确定和不可靠性，因此需要社团内的节点协同。社团内的每个节点对于事件M存在感知状态（0或1），节点对事件M的感知状态是一个二值判断，我们采用多数投票模型实现社团内部节点的协同，多数决定模型描述个体决策时主要利用邻居节点的信息，观点更新时选取数目占优的观点值。节点下一时刻选取某观点的概率正比于周围邻居所持此观点的总数目[8]。最终整个局域网络达到同步，即观点的统一。

在图1中，所有节点的观点值（即对事件M的判断值）如图1（a）所示，对于中间的节点i，共有3个邻居节点，两个邻居节点的观点值为1，另一个的值为0。因此，在下一个时刻，中间的节点i以2/3的概率选择状态 1（如图1（b）所示），1/3的概率选择状态0（即保持现有状态）。

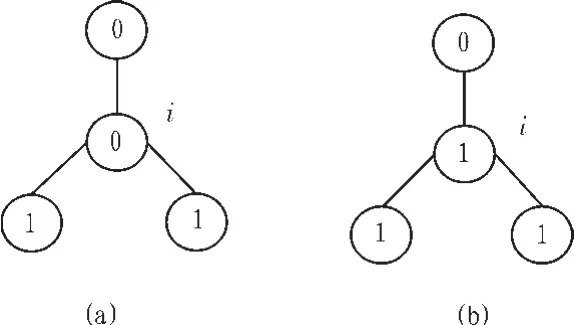
图1 多数决定模型演化示意图Fig.1 Sketch map of majority rule model

需要强调的是，CPS的感知网络中，单个节点感知的信息是确定的，节点自身对感知信息的判断是不会发生改变的。我们只是借用观点动力学的模型来模拟整个节点网络感知状态的演化，整个演化的计算过程由中心节点完成，最后确定整个局域网络对事件M的感知判断。

3）社团间进行协同 对网络进行一次社团划分之后，每个社团内部确定一个中心节点，中心节点代表社团内部运用观点动力学模型演化后对事件M的判断值，每个社团中心节点之间可以再次抽象为一个复杂网络，可以再次对这个网络进行社团分析，用观点动力学的模型进行演化。这个过程可以迭代下去，根据网络的规模确定迭代的次数，最终整个网络达到一致，即得出所有感知节点对事件M的判断

凝聚算法的时间复杂度为O（（m+n）n），其中m为网络的边的数目，n为网络的节点数目。对于多数决定模型，Krapivsky等[9]研究了方格上的二值观点传播，整个网络观点达到一致的收敛时间量级为In n，n为网络节点的数目[8]。因此，整个网络对事件M判断的收敛速度是较快的，同时本文给出的求解方法不需要事先知道事件区域的形状，节点网络能够形成对事件快速，可靠的判断。

3 结束语

本文给出一种基于社团结构的CPS感知网络中心节点选取算法以及局域内部节点的协同方法。CPS感知网络中心节点的正确选取可以优化感知网络的协同，尤其是CPS节点在大规模、高密度部署的情况下，中心节点的选取及节点之间的协同感知更加重要。本文主要讨论了感知节点对感知事件的判断是二值的情况。在有些情况下，感知节点的感知信息是连续的，这时需要采用与之相应的观点动力学模型模拟CPS感知网络节点的演化。同时，在确定事件发生后，如何确定事件源的位置也是今后需要研究的内容。

[1]李建中，高宏，于博.信息物理融合系统（CPS）的概念、特点、挑战和研究进展[C]//中国计算机学会.2009中国计算机科学技术发展报告，2010:2-17.

[2]Jiang C，Dong G，Wang B.Detection and tracking of region based evolving targets in Sensor Networks[C]//Proceedings of 14th International Conference on Computer Communications and Networks，San Diego，California，USA.2005:563-568.

[3]Fan K W，Liu S，Sinha P.Scalable data aggregation for dynamic events in sensor networks[C]//Proceedings of the International Conference on Sensor Systems（SenSys），Boulder，Colorado，USA.2006:181-194.

[4]崔筱宁.基于传感器网络的扩散性事件监测技术研究[D].合肥:中国科学技术大学，2010.

[5]Newman M E J.Fast algorithm for detecting community structure in networks[J].Phys rev E，2004，69（6）:066133.

[6]Newman M E J，Givran M.Finding and evaluating community structure in networks[J].Phys rev E，2004，69（2）:026133.

[7]解邹，汪小帆.复杂网络中的社团结构分析算法研究综述[J].复杂系统与复杂性科学，2005，2（3）：1-12.XIE Zou，WANG Xiao-fan.An overview of algorithms for analyzing community structure in complex networks[J].Complex Systems and Complexity Science，2005，2（3）：1-12.

[8]王龙，伏锋，陈小杰，等.复杂网络上的群体决策[J].智能系统学报，2008，3（2）：95-108.WANG Long，FU Feng，CHEN Xiao-jie，et al.Collective decision-making over complex networks [J]. CAAI Transactions on Intelligent Systems，2008，3（2）：95-108.

[9]Krapivsky P L，Redner S.Dynamics of majority rule in twostate interacting spin systems[J].Phys Rev Lett，2003，90（23）：238701.