斜拉桥非线性静风稳定性分析

沈 丹， 张鸣祥， 王建国

(1.南京市市政设计研究院有限责任公司，江苏南京 210008;2.合肥工业大学土木与水利工程学院，安徽合肥 230009)

随着桥梁跨径的日益增大，桥梁结构对风致响应变得更加敏感，存在静风失稳的可能性[1]。静风失稳是指结构在给定风速作用下，主梁发生弯曲和扭转，一方面改变了结构刚度，另一方面改变了风荷载的大小，并反过来增大了结构的变形，最终导致结构失稳的现象。过去，人们普遍认为大跨径桥梁的颤振临界风速一般都低于静力失稳，近年来风洞实验和理论研究表明，大跨径桥梁存在由静风引起的弯扭失稳现象。

早期的静风稳定性分析方法主要采用侧倾分析法和结构扭转发散分析法，它们均未考虑结构和静风荷载非线性因素的相互作用，难以获得准确的静风失稳临界点，属于线性分析，按线性理论计算得到的空气静力失稳风速会明显偏高。为此，文献[2]提出了用增量与迭代相结合的方法进行大跨度桥梁第2类静风稳定分析;文献[3-6]进一步提出了增量与内外两重迭代方法;文献[7]采用增量双重迭代搜索法对香港汀九桥位代表的斜拉桥进行了静风稳定分析;文献[8]提出了时域分析方法计算风致响应后的等效静力风荷载求解体系;文献[9]为了考虑结构的几何非线性提出了新的空气静力分析方法;文献[10]使用动力学方法对大跨度桥梁静风稳定性以及临界风速进行探讨。本文考虑了结构的几何非线性，将非线性静风荷载表示为风速和结构变形的函数，采用增量与内外两重迭代相结合的方法，利用ANSYS中参数化语言(APDL)编写了计算程序，对拱塔斜拉桥进行了非线性静风稳定性全过程分析。

1 斜拉桥非线性静风稳定性分析

按照文献[11]，作用在主梁单位长度的静风荷载可分解为体轴坐标系下的横向风荷载F h、竖向风荷载F v和扭转力矩M。随着风速的增加，主梁发生扭转，结构的姿态发生改变，静风与主梁的相对攻角随之改变，从而使作用其上的三分力系数发生改变，最终导致作用在主梁上的静风荷载发生改变。静风荷载可表示为风速、三分力系数和有效攻角的函数[1]，即

其中，v为平均风速;Ch(α)、Cv(α)、Cm(α)分别为主梁在有效攻角下沿结构体轴坐标系方向的阻力、升力、升力矩系数;α为有效攻角，α=α0+θ，α0为风的初始攻角，θ为结构的扭转角;ρ为空气密度;D、B分别为主梁的侧向投影高度和宽度。从(1)式可以看出静风荷载是结构变形的函数，计算中必须考虑这一非线性因素的影响。

根据空间杆系结构的稳定性理论和有限元法，大跨径桥梁静风稳定性问题的有限元平衡方程[1]如下:

其中，u为结构的节点位移向量;K(u)为结构的刚度矩阵，刚度矩阵的系数与节点位移相关; Fh(α)、Fv(α)、M(α)分别为结构体轴方向上所受的阻力、升力和升力矩;f是静风荷载引起的等效节点荷载向量，与阻力、升力和升力矩有关。

从(1)式和(2)式可以看出，结构的刚度是结构变形的函数，右端所表示的静风荷载也是结构变形的函数。结构平衡(2)式为非线性方程组。非线性方程的求解方法有增量法、迭代法和增量-迭代法。本文采用增量与内外两重迭代相结合的方法求解(2)式。将风速按一定比例增加，内层迭代主要是进行结构的非线性计算，而外层迭代则是为了寻找结构在某一风速下的平衡位置，相应的非线性增量平衡方程为:

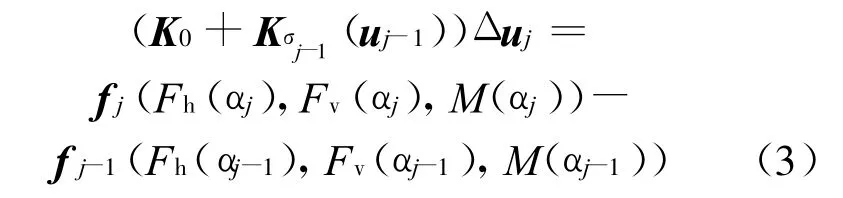
其中，K0为线弹性刚度矩阵;Kσj-1(u j-1)为第j-1步时，由第i级静风荷载引起的几何刚度矩阵; Δu j为第i级静风荷载引起的第j步状态时位移增量;fj为第i级静风荷载引起的第j步有效攻角αj的等效节点力向量;f j-1为第i级静风荷载引起的第j-1步有效攻角αj-1的等效节点力向量。在进行空气静力稳定性分析前，先确定斜拉桥的成桥状态下恒载内力，具体实施步骤如下:

(1)自重作用下线性求解。

(2)提取主梁单元扭转角，计算该状态三分力系数，此时主梁有效攻角等于初始攻角α0。

(3)假定初始风速v0和风速步长Δv，由(1)式可以计算出作用在结构上的静三分力。

(4)在当前风速下，采用牛顿-拉普生方法(New ton-Raphson)进行结构几何非线性求解，得出结构位移。

(5)提取主梁扭转角进而在该级风速下进行三分力系数修正，重新计算结构的静风荷载。

(6)检查三分力系数的欧几里得范数是否小于允许值，即

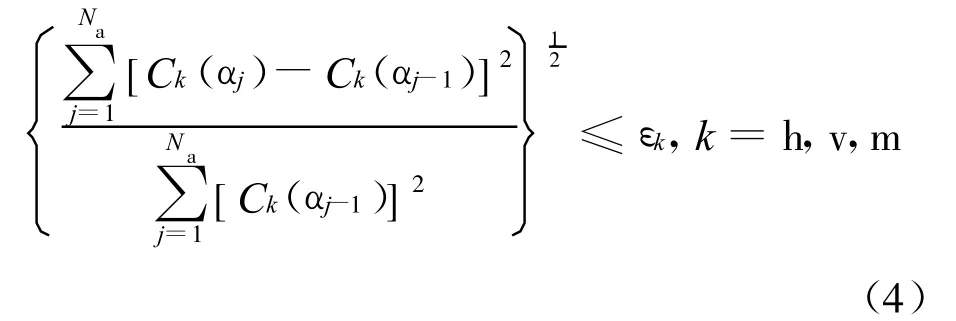
其中，N a为受静风荷载作用的节点总数;Ck分别为阻力系数C h、升力系数C v和升力矩系数C m;εk为阻力系数Ch、升力系数Cv和升力矩系数Cm的允许误差，可取0.005。

(7)如果小于允许值，说明本级风速计算结果收敛，输出结果，按预定步长增加风速，进行下一级风速计算。如果大于允许值，重复步骤(4)～(6)，若迭代次数超过预定的次数，说明本级风速难以收敛，将风速步长减半，返回步骤(4)重新计算，直至相邻2次风速之差小于预定值为止。

2 算 例

2.1 基本数据

本文以某拱塔斜拉桥为例，来考察斜拉桥的静风稳定性。该桥是一座三塔四跨双索面斜拉桥，全桥跨径布置为120 m+260m+260 m+ 120 m=760m。主梁为混凝土Π形梁，主梁梁高为3.2m，翼缘和腹板尺寸如图1所示，该桥中塔和边塔为拱形预应力混凝土塔，塔高分别为106m和88m。斜拉索采用平行钢绞线拉索，主梁标准索距为7 m，塔上标准索距为2 m。钢绞线强度为1 860 MPa，全桥共设50对斜拉索。

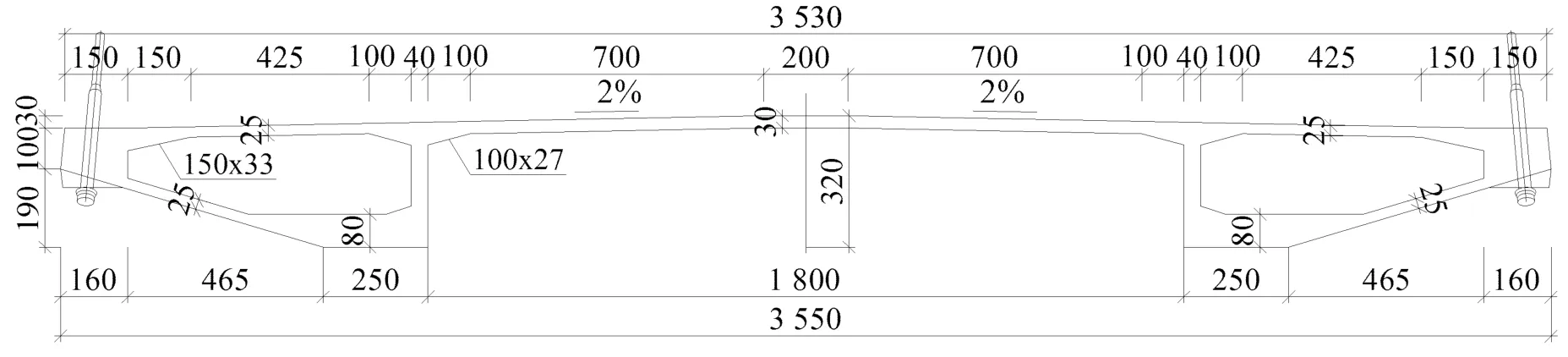
图1 斜拉桥主梁标准断面

2.2 桥梁结构的有限元离散

为了保证对结构进行合理的抽象和简化，保持结构的刚度、质量的等效性及其空间分布，保证支撑条件真实反映结构的工作行为，用空间杆单元和梁单元来模拟整个结构，主梁主塔采用空间梁单元Beam188模拟，斜拉索用索单元 Link10模拟以考虑索的非线性影响，斜拉桥采用鱼骨式模型，全桥共有700个单元，其中主梁单元110个，塔单元390个，索单元200个。结构三维有限元离散模型如图2所示。

图2 拱塔斜拉桥三维有限元离散模型

2.3 计算结果

由于大气边界层的强风主要是水平方向的，但可能有+3°～-3°攻角的微小变化，则静三分力系数随攻角有相应的变化，因此偏安全地取攻角+3°～-3°范围内的最大值，计算桥梁结构在静风荷载下的主梁和主塔的效应。通过对主梁进行节段模型试验测得主梁体坐标系下的静三分力系数，如图3所示。

模拟成桥状态风速加载全过程，初始风攻角取3°，以0m/s的初始风速进行逐级加载，采用静力扭转发散公式计算的临界风速为260 m/s;不同初始风攻角下，计入几何非线性的计算结果见表1所列。

图3 成桥状态主梁三分力系数曲线

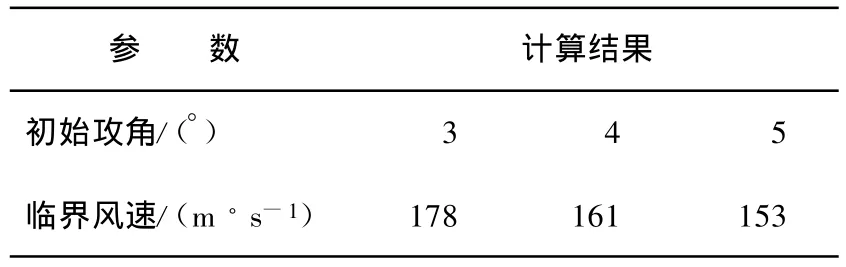
表1 不同初始风攻角的计算结果

3°初始风攻角时，主梁主要截面位置处竖向位移、横向位移和扭转角随风速的变化过程，如图4所示。

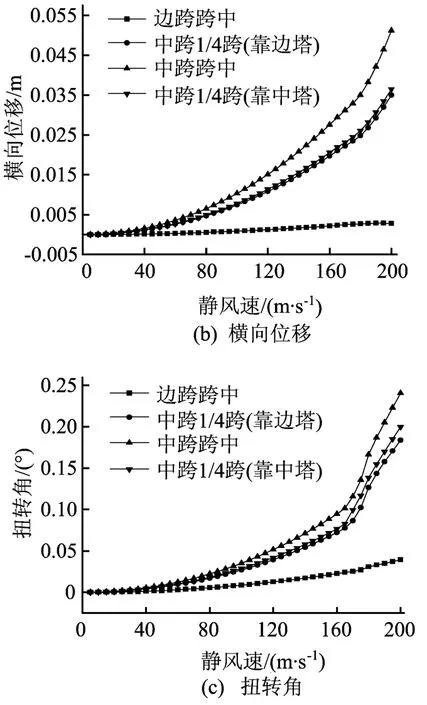
图4 主梁竖向位移、横向位移及扭转角随风速的变化

不同初始攻角下主梁跨中截面竖向位移随风速的变化过程，如图5所示。

图5 不同初始攻角跨中竖向位移随风速的变化

3 结 论

(1)不考虑非线性会使计算的结构静风失稳临界风速偏大，偏于不安全。

(2)3°风攻角时，在风速不断增加的过程中，结构的竖向、横向和扭转变形都呈现明显的非线性增长特征，表明此拱塔斜拉桥在静风作用下的变形是主梁竖弯、侧弯和扭转变形完全耦合的过程。

(3)主梁中跨跨中处的竖弯、侧弯和扭转变形均大于中跨1/4跨处，中跨1/4跨处较明显大于边跨跨中。这表明在静风荷载作用下，主梁的位移值沿梁长方向明显分布不均，跨中位置大于其它位置。

(4)在不同的初始攻角下，主梁的竖弯变形差异较大。0°～3°范围内，升力系数曲线、升力矩系数曲线斜率较大并且穿过零点。随着初始风攻角的增大，斜拉桥的静风稳定性会略有下降。

[1] 巩海帆.现代桥梁抗风理论与实践[M].北京:人民交通出版社，2005:412-444.

[2] 方明山，巩海帆，肖汝诚.大跨径缆索承重桥梁非线性空气静力稳定理论[J].土木工程学报，2000，13(3):73-79.

[3] 程 进，肖汝诚，巩海帆.大跨径斜拉桥非线性静风稳定性全过程分析[J].中国公路学报，2000，13(3):25-28.

[4] 程 进.缆索承重桥梁非线性空气静力稳定性研究[D].上海:同济大学土木工程学院，2000.

[5] Cheng Jin，Jiang Jianjing，Xiao Rucheng，et al.Advanced aerostatic stability analysisof cab le-stayed bridgesusing finite-elemen tmethod[J].Computers and Structu res，2002，80:1145-1158.

[6] 胡小伦.大跨度斜拉桥颤抖振响应及静风稳定性分析[D]，上海:同济大学土木工程学院，2006.

[7] 韩大建，邹小江.大跨度斜拉桥非线性静风稳定分析[J].工程力学，2005，22(1):206-210.

[8] 江 勇，王肈民，王洪涛.大跨空间钢结构时域等效静力风荷载理论研究[J].合肥工业大学学报:自然科学版，2008，31(2):202-206.

[9] Zhang Xinjun.Advan ced aerostatic analysis of long-span suspension bridges[J].Jou rnal of Zhejiang University:Science A，2006，7(3):424-429.

[10] Tsay J Y，Yang Y B.Aerodynamic instability of cablesuppo rted bridges considering the initial deformed shape due to dead loads[J].Int J of Structural Engineering，2009，1(1):71-92.

[11] 项海帆，林志兴，鲍卫刚.公路桥梁抗风设计指南[M].北京:人民交通出版社，1996:20-23.