基于模糊控制的规则化描述方法研究

李鸿明， 毕 翔，2， 魏振春，2， 韩江洪，2， 王启忠

(1.合肥工业大学 计算机与信息学院，安徽合肥 230009;2.合肥工业大学安全关键工业测控技术教育部工程研究中心，安徽合肥230009;3.安徽国投新集能源股份有限公司 刘庄煤矿，安徽颖上 236200)

0 引 言

离散事件动态系统(discrete event dynamic system s，简称DEDS)是由异步、突发的事件驱动状态演化的动态系统，系统的输入输出是离散量，难以建立精确的数学模型[1]。产生式规则主要用于专家系统中，具有自然直观、格式清晰、便于推理的特点，因而得到了广泛的使用。规则化描述方法(rule description method，简称RDM)是一种将产生式规则应用于DEDS，用来描述DEDS中各对象间行为关系的方法。该方法已应用在车身总线控制系统、皮带机集群控制系统中，并且取得了较好的效果[2，3]。

但是在实际的生产应用中，是以混合动态系统(HDS)为主，包括DEDS和连续变量动态系统(CVDS)[4]。在此类系统中，存在着连续变量的输入与输出，因为RDM可使用的范围是离散变量，对连续变量的描述存在不足，使得系统必须引入另一个控制方法，增加了系统的复杂度和设计难度。为了简化系统设计的结构，需使RDM同样适用于连续变量。模糊控制是以模糊集合论、模糊语言变量及模糊逻辑推理为基础的，模拟人的近似推理和决策过程[5]，和RDM相似的都是以规则作为系统输出的参照，因此RDM可以引用模糊控制的模糊概念来编写规则，同时在系统中引入模糊控制对连续变量的处理方式，使RDM适用于连续变量动态系统。

1 DEDS的规则化描述方法

RDM采用类似产生式规则(IF…THEN…)的规则形式，将系统中相关的事件和动作写成一条规则，具有规范、简洁、贴近自然语言、易于理解和修改的特点[6-8]。每条规则都由左件和右件2部分组成，左件相当于条件，右件相当于动作。左件和右件均由因子组成，因子不止一个时，中间用“&”相连，表示“逻辑与”，语法形式如下:

＜因子＞&＜因子＞&…&＜因子＞= =＜因子＞&＜因子＞&…&＜因子＞，

因子的定义如下:＜因子＞::=[＜因子名＞:＜因子值＞]。

因子是规则中的最小单元，每个因子代表系统中的一个对象，因子名为该对象名，因子值代表该对象当前的状态。

在采用RDM的系统中，系统被分为驱动层和逻辑层。驱动层包括输入驱动和输出驱动。当某一个对象的状态发生变化时，触发生成该对象的因子，将其封装在一个通信消息中发送给逻辑层。逻辑层相对底层是一个独立的模块，把系统中的控制策略剥离出来，包括规则库和推理模块。当逻辑层收到通信消息后，提取因子信息，搜索规则库激活相关规则，被成功激活规则的右件因子则作为输出，发送给输出驱动模块。输出驱动模块将规则的右件因子解释并执行。逻辑层和驱动层之间的耦合程度较低，可以很方便地进行修改和完善，提高了系统的适应性。

2 基于模糊理论的RDM

2.1 知识量化为模糊规则

在自然语言中，人们常用一些模糊性的词语交流，使得可以用较少的言辞传递最大的信息量，如“大”、“小”、“快”、“慢”等[5]。如用人的思维逻辑去控制车速，“当车速稍慢的时候，则轻踩油门”，车速是连续变化的，不能简单地用一个状态或数值去表示，但可以使用这些模糊的语言值来描述其状态，进而描述整条规则。RDM是一种贴近自然语言的描述方法，因此也可以采用模糊语言值的方法，来描述连续系统的控制规则。

将输入和输出变量进行量化，映射为模糊语言值，因子中的因子值用模糊语言值代替传统的精确值，由这种因子组合成的规则，称为模糊规则。如上述的车速控制，使用RDM的形式描述为＜车速:稍快＞==＜油门:轻踩＞，因为模糊规则使用的因子值是模糊量，于是在采用RDM系统的驱动层中，需要将输入的精确值转化为模糊量发送到推理模块，将推理模块发送的模糊量转化为精确值进行输出。在此，引入模糊控制中的模糊化和解模糊化方法，实现精确→模糊、模糊→精确的转化过程。结合RDM系统自身的结构特点，将模糊规则并入规则库中，整个系统共用一个规则库，保持逻辑层的独立性。

2.2 模糊化

在模糊控制中，模糊化方法就是将输入的精确值转化为该变量在其论域上的模糊集合及其相应的隶属度[5]。这里输入变量 x的隶属函数μAi(x)采用三角形分布形式，即

其中，ai、bi、ci分别是三角形3个顶点的横坐标。

如图1所示，将模糊化处理模块并入输入驱动模块中，保持系统原有层次结构，驱动层和逻辑层仍然以传递消息的方式进行通信。原输入驱动模块分为2个子模块，一个用于处理连续变量的模糊化模块，一个用于处理离散量的离散量转换模块。此时，层与层之间传递的通信消息就需要包括因子名、模糊值和对应的隶属度，结合RDM的语法形式，通信消息的格式如下:

[＜因子名＞:＜模糊值1-隶属度1＞:＜模糊值2-隶属度2＞:…:＜模糊值N-隶属度N＞]，N表示模糊值的个数。

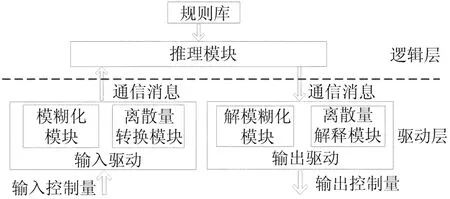
图1 采用基于模糊控制的RDM系统结构图

2.3 推理过程

逻辑层收到驱动层发送的通信消息，需要进行规则推理。推理分2个步骤:

(1)确定激活哪些规则。将通信消息中所有隶属度大于0的模糊值过滤出来，与对应的因子名组成因子，因子名相同的因子归并成为一个集合A，那么一个输入量将会生成一个集合。对于一个有m个输入量的系统，则会生成m个集合{A1，A2，A3，…，Am}，这m个集合的笛卡尔乘积D=A1×A2×A3×…×Am。遍历整个规则库，依次取出每条规则，如果规则左件所包含的因子与集合D中任意一个子集相同，此条规则将会被激活，匹配不到的子集将丢弃不用。

(2)量化被激活规则的左件隶属度。一个多输入的系统，被激活的规则左件包含了多个因子，并且各个因子的隶属度不一定相同，因此规则左件的隶属度需要重新定义。对被成功激活的规则左件的隶属度采用取小的原则计算[5]，即以左件所包含的因子中最小的隶属度作为此条规则左件的隶属度，即

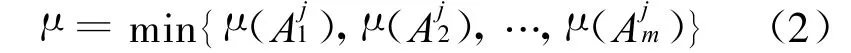
每条被激活的规则都至少有一个推荐的结论，即右件最少包含一个因子。将被成功激活的规则右件包含的因子与规则左件隶属度μ组合，具有相同因子名的因子封装在一条通信消息中，发送给输出驱动。

2.4 解模糊化过程

对于传统规则推理出的是离散量，可以直接被驱动程序执行，但是对模糊规则推理出的是模糊量，需要将其转化为可被驱动理解的精确值，这个过程称为解模糊化[5]。这里解模糊使用重心法，其计算公式为:

其中，∑表示代数和;zi表示隶属函数的质心;∫μi(z)表示隶属函数μi(z)下的面积;z0为输出值。

图1中，将解模糊化模块并入输出驱动中，保持系统原有的层次结构。这样，输出驱动模块就被分为2个子模块，用于输出连续变量的解模糊化模块和用于输出离散变量的离散量解释模块。

3 仿 真

模拟小车在一条有障碍物的高低不平的直线道路上行驶，要求是匀速运动的，并且在遇到障碍物时及时避让，使用平台VC 6.0。

为了简化过程，小车的采用频率为10 H z，控制车速v h=20m/s，始时车速为0。系统的输入量有速度偏差e(t)=vt-v h和偏差变化率d e(t)/ d t，即小车的加速度a，系统的输出是油门开度K，当K＞0时，踩油门;K＜0时，踩刹车;K=0时，保持不变，K∈[-100%，100%][9]。以加速度a-表示坡对车辆速度的影响，a-＞0时，表示下坡;a-＜0时，表示上坡;a-=0时，表示平坦，a-∈[-5，5]。道路共3个车道，障碍物静止并随机放置在某个车道上。油门开度对车辆的驱动加速度为a+，小车在t时刻车速为:

其中，vt0表示在t0时刻的车速a+d t为(t-t0)时间内控制加速度对速度的影响a-d t为(tt0)时间内坡度对汽车速度的影响。

将输入和输出量在各自的论域上划分为5个等级{-2，-1，0，1，2}，对应的语言值{负大、负小、零、正小、正大}，英文字头缩写为{NB，NS，ZO，PS，PB}，其隶属函数如图2所示。

图2 隶属度函数

使用RDM描述的车速控制规则如下:

障碍物在此是一种离散量的形式出现，共3个车道{1，2，3};车辆检测当前5个方向{左2，左1，前，右1，右2}，左2表示左边第2个车道，左1表示左边第1个车道，右2和右1相同;用1、0分别表示障碍物的有无，根据当前小车所在车道和前方5个方向的障碍物情况，生成当前状态因子。避让的规则如下:

系统的仿真结果如图3、图4所示。图3是小车速度曲线图，从中可以看出，对复杂的路面，车速保持在vh上下震荡。图4是仿真使用的坡道，造成曲线中几次大的震荡，是由于陡坡的作用。

图3 仿真实时速度曲线

图4 仿真坡道

小车对障碍物的避让，如图5所示。采用基于模糊控制的RDM系统对离散事件进行处理，从图5中可以看出，对离散事件处理能力没有影响。

图5 小车对障碍的避让

4 结束语

针对RDM对连续变量描述的不足，提出了基于模糊控制的规则化描述方法，经仿真验证表明，该方法能够较好地应用于连续变量动态系统，扩展了RDM的使用范围，同时对原系统有很好的兼容性。与采用传统RDM的系统相比，采用基于模糊控制的RDM系统，保留原系统的层次结构和对离散变量的处理方式，输入和输出驱动中分别引入模糊化和解模糊化模块，规则库中增加了模糊规则，实现了连续变量的输入输出，有效地降低了混合动态系统结构的复杂度，使得RDM可适用于更加复杂的系统。

[1] 郑大钟，赵千川.离散事件动态系统[M].北京:清华大学出版社，2001:1-339.

[2] 韩江洪，魏振春，张本宏，等.总线式车身控制系统的规则化建模方法[J].汽车工程，2006，28(12):1121-1124.

[3] 韩江洪，郑淑丽，陆 阳，等.离散事件控制系统规则化描述方法的研究[J].合肥工业大学学报:自然科学版，2005，28 (9):1081-1084.

[4] 龙 德，崔建江，徐心和，等.基于知识的分层事件调度混杂系统仿真策略[J].系统仿真学报，2003，15(12): 1805-1807.

[5] Passino K M，Yurkovich S.Fuzzy control[M].北京:清华大学出版社，2001:21-103.

[6] Wei Zhenchun，H an Jianghong，Lu Yang，et al.Hierarchical m odeling and control of discrete even t control sy stem s based on rule description method[J].Proceedings of the 2006 IEEE In ternational Conference on M echatronics and Au tomation，2006:2179-2183.

[7] 韩江洪，张亚琼，魏振春，等.基于规则的离散事件系统模型与规则匹配研究[J].系统仿真学报，2008，20(6): 1394-1396.

[8] 肖冰冰，张维勇，毕 翔.一种基于规则化描述方法的验证技术[J].合肥工业大学学报:自然科学版，2010，33(5): 674-678.

[9] 刘文光，何 仁.考虑油门开度快速变化的自动变速器换挡控制策略[J].农业机械学报，2009，40(9):16-19.