单向平动微位移工作台的静刚度分析

朱仁胜， 沈 健， 刘永梅

(1.合肥工业大学 机械与汽车工程学院，安徽 合肥 230009;2.清华大学 电力系统与发电设备控制及仿真国家重点实验室，北京100084;3.安徽电力濉溪供电有限责任公司，安徽淮北 235100)

0 引 言

柔性铰链具有体积小、无间隙、无机械摩擦、成本低廉及无需润滑等优点，在精密工程中有广泛的应用，例如精密工作台、纳米定位技术、微加速度器、微夹持机构和显微装置等[1-5]。

目前，在研究微动工作台中大多的相关研究均基于伪刚体模型或其它类似的建模方法，即将柔性铰链视为理想的转动副，其转轴中心处于薄壁中心，只考虑柔性铰链的弯曲变形。这些模型中，柔性机构的每一个柔性铰链均被等效为弯曲弹簧或拉压弹簧[6，7]，柔性铰链被视为单自由度模型。采用这种方法虽然对微动工作台的动力特性分析提供方便，但是由于模型简化程度较大，分析得到的结果误差也较大，结果的准确性难以保证。

本文采用能量法，建立柔性铰链的单元刚度矩阵，即把柔性铰链视为三自由度单元，并在此基础上建立了单向平动微位移工作台的有限元数学模型。通过对单向平动微位移工作台分析表明，这种方法不仅计算简单，而且精度较高。

1 柔性铰链单元刚度矩阵

柔性铰链的几何结构、受力及变形如图1所示。

柔性铰链的几何尺寸为:切割半径R，铰链最薄处的厚度t，铰链的宽度b，圆心角θm。假设柔性铰链的右端为相对固定端，左端受到力和力矩Fx、Fy、Mz的作用，左端的变形为u、v、αz。

把柔性铰链看作变截面梁单元如图2所示。

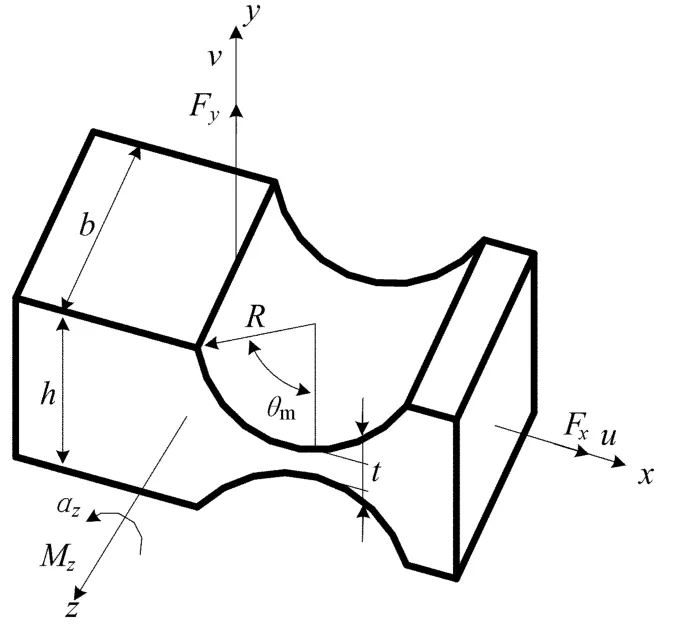
图1 柔性铰链的几何结构、受力和变形

图2 变截面梁单元

显然x截面的内力分量可以表示为:

单元的应变能为:

其中，A s(x)为x截面的有效剪切面积。根据卡氏第二定理，则有:

在圆心角θ(x截面)处取微元体dθ进行研究，把从0～l上的积分转化到从-θm～θm上的积分。微元体的厚度为:

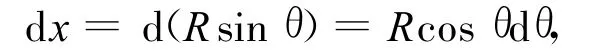
微元体的高度为:

微元体截面面积为:

微元体截面沿z方向的惯性矩为:

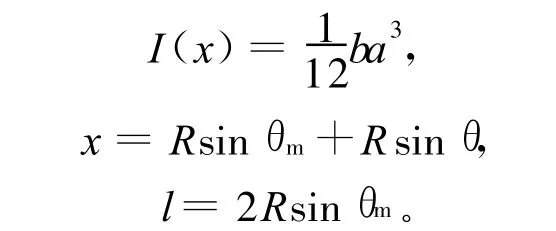
根据积分公式:

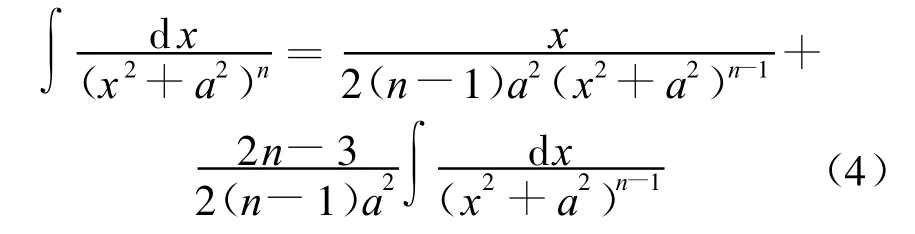
可以得到联系单元i端节点位移和节点力的关系式为:

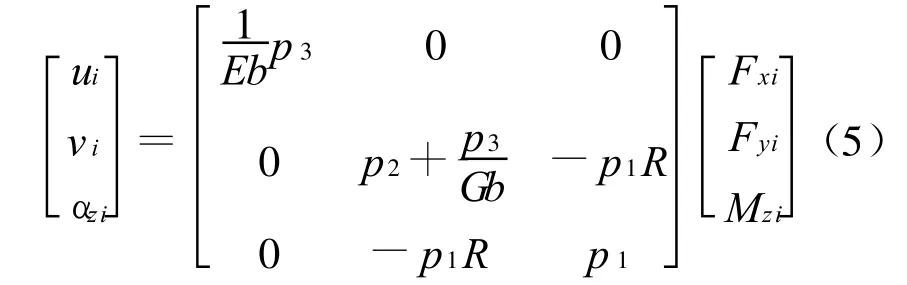
其中，E、G分别为材料的弹性模量和剪切模量，则有:

(5)式、(6)式中:

根据文献[8]，有

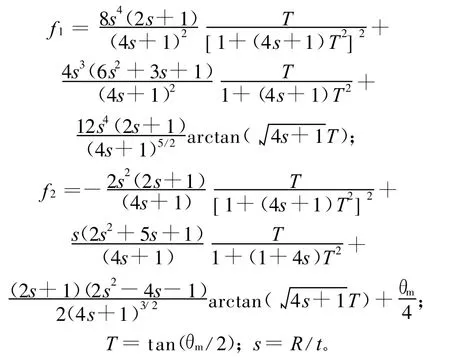
(6)式中矩阵Dii即为单元i端的柔度矩阵，对于该柔度矩阵求逆可得到刚度矩阵K ii为:

其中

单元平衡条件为:

即

其中，H为单元平衡矩阵。

根据文献[9]可以得到单元刚度矩阵Ke为:

则有:

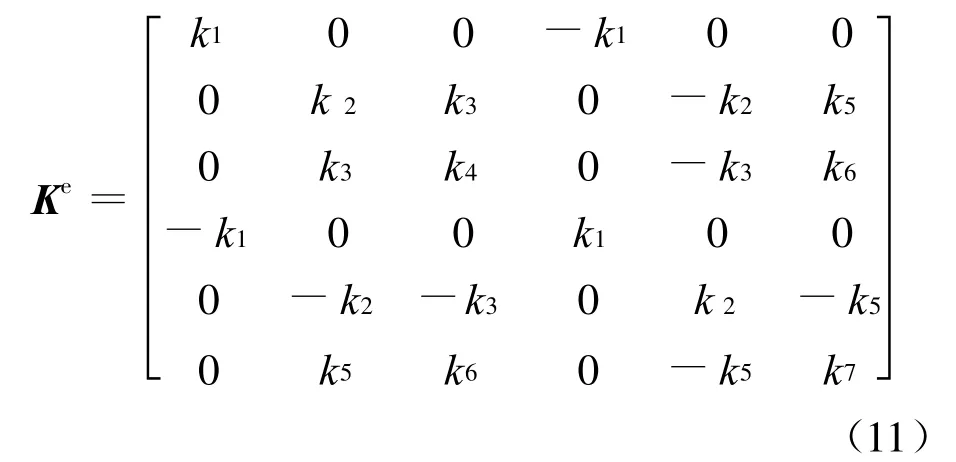
其中

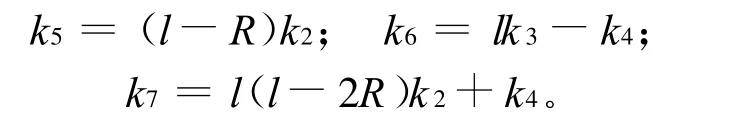
若θm=π/2，则

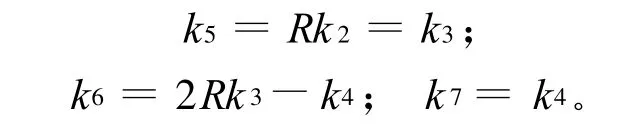
单元在整体坐标系下的刚度矩阵为:

其中，T为坐标转换矩阵，即

其中，γ为单元与结构整体坐标系的夹角。

2 连杆单元刚度矩阵

根据文献[10]，可以得到框架单元在局部坐标系下的刚度矩阵:

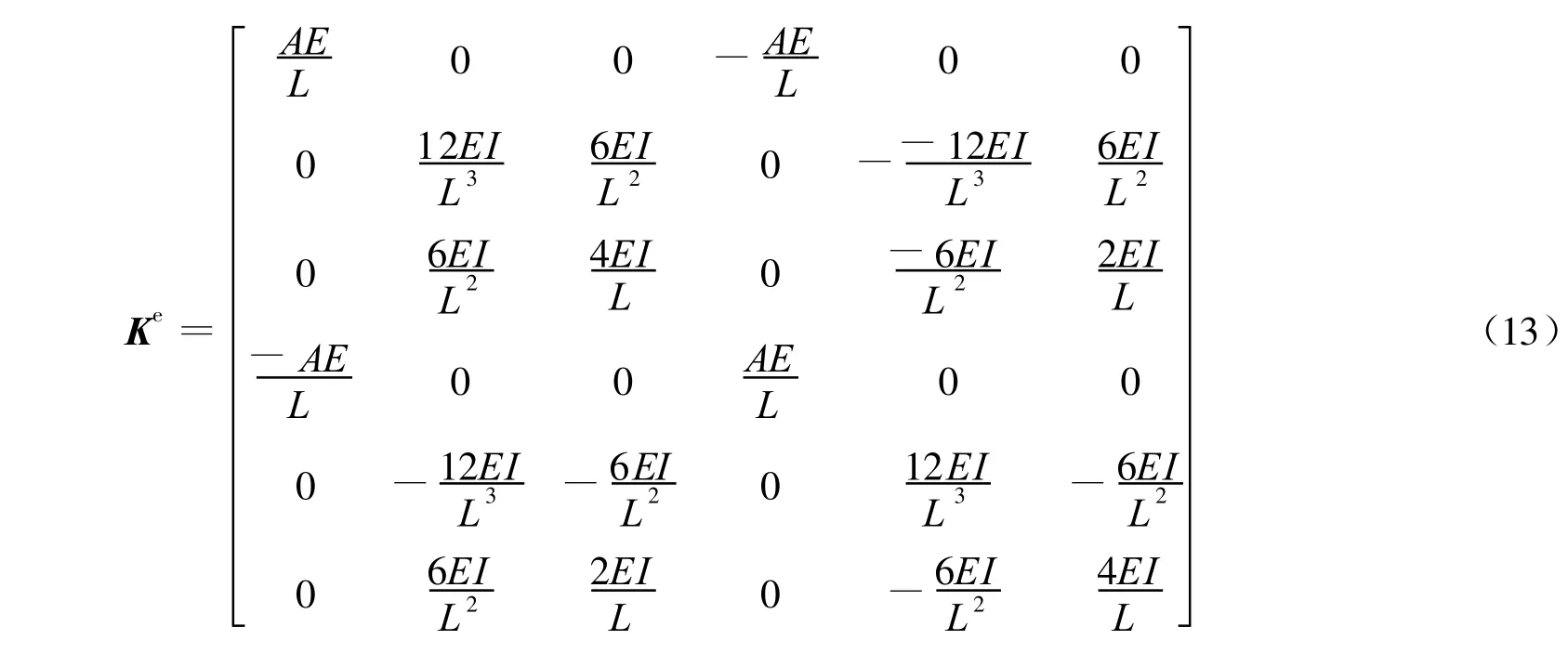
其中，A为单元截面面积;L为单元长度;I为单元截面惯性矩。

连杆单元在整体坐标系下的刚度矩阵为:

组合柔性铰链单元刚度矩阵和连杆单元刚度矩阵，就可以得到结构的总体刚度矩阵，即

3 单向平动微位移工作台的分析与计算

单向平动微位移工作台为对称平行四杆机构，如图3所示。图3为离散化后的模型，驱动力施加在方框内对称面处，方向向上。

用有限元分析软件对工作台进行模拟计算并与理论模型计算值相比较。微位移工作台采用材料为65M n，材料的弹性模量E=200 GPa，泊松比ν=0.288，柔性铰链采用直圆型，即θm=π/2。

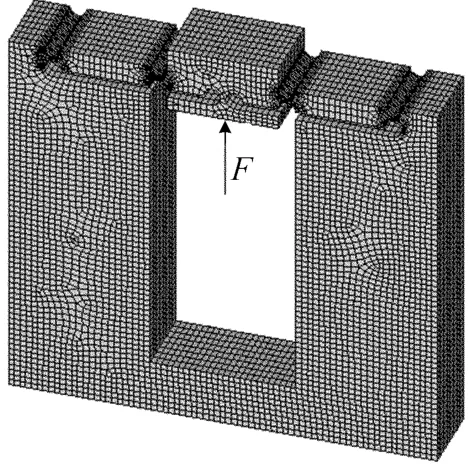
图3 微位移工作台的有限元模型

单自由度微位移工作台的变形主要发生在柔性铰链部分，其它部分的变形很小，根据模型的对称性仅取模型的1/2进行分析。理论模型分为5个单元，每个单元有2个节点，每个节点有3个自由度，组合柔性铰链单元刚度矩阵和连杆单元刚度矩阵得到机构的总体刚度矩阵K为18×18阶对称矩阵，如图4所示。图4中L1、L2、L3为连杆单元，粗短线代表柔性铰链。

位移向量为:

由于模型仅在节点6施加一个沿V方向的集中力载荷F，其载荷向量为:

模型的位移边界条件如下:

(1)节点1的平动、转动位移均为零，即

(2)对称约束条件，节点6所在的截面为对称面，即

施加载荷和边界条件后，可以得到结构的平衡方程:

解线性方程组(16)，可以得到工作台的位移输出值，表1中理论解即为v6的值。

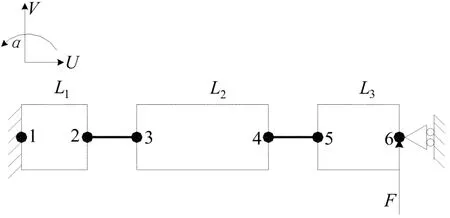
图4 理论计算模型

有限元分析软件计算模型如图3所示，模型采用8节点的Solid45单元，每个节点3个自由度。选取不同的柔性铰链参数:R=1.8，2.0，2.5，t=0.7，0.9，1.0;连杆参数L2=18，20，22。施加不同的载荷F，用2种方法计算微位移工作台的输出位移，见表1所列。

计算结果表明，在选取的参数范围内，理论计算模型与有限元软件计算结果相吻合。

表1 理论法与模拟法计算工作台输出位移

4 结束语

本文通过对柔性铰链的分析，把柔性铰链视为变截面梁单元，建立柔性铰链单元刚度矩阵，与连杆单元刚度矩阵组合，建立单向平动微位移工

作台的有限元计算模型。选取不同的柔性铰链参数，用有限元分析软件对工作台进行分析计算并与理论模型计算结果相比较，结果表明2种方法计算结果相吻合。在一定参数范围内，理论计算模型能分析单向平动微位移工作台的位移输出特性，计算误差较小，计算简单。

本文的设计计算方法对其它类型的柔性铰链分析以及对平面连杆机构的微位移工作台的设计有一定的参考意义。

[1] Zhang D，Chang C，Takahito O，et al.A piezodriven XY-m icrostage for mu ltiprobe nanorecording[J].Sensors and Actuators A，2003，108:230-233.

[2] Sebastian A，Srinivasa M S.Design m ethodologies for robust nano-positioning[J].Control Systems Technology，2005，13(6):868-876.

[3] X iong X，Zou Q，Deren L，et al.Balance-approach for load-displacemen t measu rement of m icrostructures[J]. M echatronics，1998，8:549-559.

[4] Peichel D，Marcus D，Read N R，et al.Silicon fab ricated subm icrometer stepper motor for m icrosurgical procedures [J].M icroelectromechanical System s，2002，11(2): 154-160.

[5] Zhang H，Higuchi T，Nishioki N.Dual tunneling-unit scanning tunneling m icroscope for length measu rement based on cry stalline lattice[J].J Vac Sci Technol B，1997，151:174-177.

[6] 于靖军，周 强，毕树生，等.基于动力学性能的全柔性机构优化设计[J].机械工程学报，2003，39(8):32-36.

[7] X iao P S，H enry S Y.Design of com pliant m icroleverage m echanisms[J].Sensors and Actuators A，2001，87: 146-156.

[8] 朱仁胜，沈 健，谢祖强，等.双轴柔性铰链柔度的设计计算[J].合肥工业大学学报:自然科学版，2009，32(9): 1370-1373.

[9] 张元海.一个改进的平面梁单元[J].计算力学学报，2002，19(1):109-111.

[10] 谢贻权，何福保.弹性和塑性力学中的有限单元法[M].北京:机械工业出版社，1981:50-120.