DECS的产生式规则建模与规则的结构错误检测

毕 翔， 王科富， 魏振春， 韩江洪， 张 宏

(1.合肥工业大学 计算机与信息学院，安徽合肥 230009;2.合肥工业大学安全关键工业测控技术教育部工程研究中心，安徽合肥230009;3.安徽恒源煤电股份公司，安徽宿州 234000)

基于规则的系统(Rule-based System，简称RBS)已经被广泛用于各类专家系统中，用于刻画领域知识及推理规则，通过逻辑推理，实现领域内困难问题的有效求解[1]。系统的结构具有知识与推理机分离特点，当知识改变时，只需更新知识库，而推理机不用改变，所以系统具有很好的可维护性和可扩展性。离散事件控制系统(Discrete Event Control Systems，简称DECS)是指系统由离散事件驱动，当一个离散事件到来时，会引发系统中某些对象状态发生变化，这些变化又会按照某种规则使其它对象状态发生改变。系统遵循的是复杂的人为规则[2-5]，所以在对离散事件系统进行建模时，采用基于规则的系统架构，系统的控制逻辑方案由规则库描述。当系统控制逻辑改变时，只需更新规则库。此时控制程序只需接收系统对象状态消息，将系统输入消息与规则库进行匹配，得到待执行的匹配结果，实现规则与控制分离，使系统具有很好的可维护性和可扩展性。系统结构如图1所示。

RBS的建立需要解决2个基本问题:①将系统模型用规则表示;②对生成的规则库进行结构验证。本文针对离散事件系统模型定义，采用产生式规则表示法描述系统规则，同时对生成的规则库进行逻辑结构验证，为复杂系统设计提供一种可行方案。

图1 基于规则的系统结构

1 离散事件系统中规则的表示

1.1 产生式规则表示法

产生式规则表示法是由美国数学家波斯特(Post)于1943年提出的，它依据人类大脑记忆模式中各种知识块之间大量存在的因果关系，并以IF…THEN…的形式表示出来[6]。产生式规则表示法形式单一，便于理解，易于计算机编码实现，且规则之间相互独立，规则的结构化较好，有利于知识的提取和形式化，其求解问题的过程同人类的认知过程相似，因而广泛应用于各类专家系统及人工智能、模糊控制等领域[7]。

结合产生式规则表示法，分析离散事件系统运行过程:当一个事件发生时，会引起系统对象状态发生变化，这些对象状态的变化会按照某种规则改变其它对象的状态。简而言之就是如果(IF)某些对象状态发生改变，那么(THEN)有可能改变其它对象的状态，这种叙述完全符合产生式规则表示法中的IF…THEN…表达形式。

1.2 离散事件系统模型

离散事件系统模型可用一个5元组来表示:

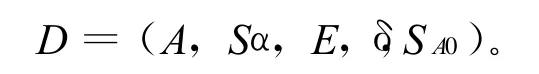
其中，A代表系统实体对象集，A={α1，α2，…，αm}，|A|=m表示系统实体个数;Sαi表示实体对象αi的状态集合，即(1)式，αij表示αi的第j个状态，|Sαi|=λi表示实体对象αi的状态个数;E表示外部事件的集合，它触发实体对象的状态发生变化，可由实体对象的状态转移式集合表示。

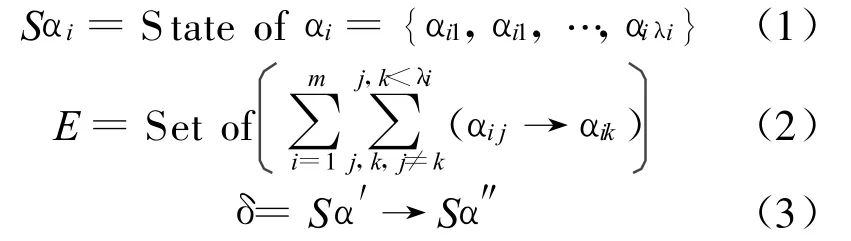
其中，δ表示系统内部的状态转移，即表示系统中某些实体对象状态发生变化时将导致其它实体对象状态发生改变，它发生在外部事件触发之后，即。其中，Sα表示实体集A中所有实体在某一时刻的状态集合;SA0为系统对象的初始状态集;e为由随机事件触发;δ表达系统内部状态转移关系，可见δ是系统的运行机制，实例化后就是系统运行的规则。

用IF…THEN…形式描述δ:IF Sα′THEN Sα″，即如果Sα′满足，将使Sα″发生。

1.3 产生式规则表示法举例——皮带运输系统

一条几百至上千米的皮带运输线，需要多台皮带机串联组成，每台设备由电机控制箱和皮带保护箱组成，每个部件有若干器件组成。此时，系统要研究设备与设备之间、设备与部件之间、部件与器件之间状态关联问题，这些问题都是由离散事件驱动的且是随机的，如开机事件、关机事件、各种报警事件，所以称皮带运输系统属于离散事件系统。

本文着重讨论皮带运输系统的停机问题，系统停机分为顺停和逆停2种停机方式。顺停是指从上游设备往下游设备依次停机，即1号设备停、2号设备停…直到最后一台设备。每台设备收到上游临近设备顺停机消息时要延时一个走带时间，把皮带上的货物运完，保证自己空载停机。逆停是指当整个系统中某一台皮带机设备发生故障时，此时这台皮带机及其上游设备执行逆停操作(立即停机)，这台皮带机下游所有设备执行顺停操作。

分析整个停机过程，系统含有3个实体对象:①皮带机状态——运行、顺停、逆停;②电机控制箱状况——正常、故障;③皮带保护箱状况——正常、故障。当电机控制箱状况和皮带保护箱状况发生故障，则皮带机状态为逆停。当上游邻近皮带机状态逆停或顺停，则该皮带机状态为顺停。当下游邻近皮带机状态为逆停或顺停，则该皮带机状态为逆停。

这里将自身皮带机状态表示为皮带机状态(i)，上游邻近皮带机状态表示为皮带机状态(i-1)，下游邻近皮带机状态表示为皮带机状态(i+1)。

“电机控制箱状况”和“皮带保护箱状况”状态值由“正常”变为“故障”是由各种传感器消息获得，属于内部随机事件。邻近皮带机状态改变消息，属于外部随机事件。

用离散事件系统定义的5元组D=(A，Sα，E，δ，SA0)描述。

A={皮带机状态，电机控制箱，皮带保护箱};

Sα={{运行、逆停、顺停}，{正常、故障}，{正常、故障}};

SA0={(皮带机状态:运行)，(电机控制箱:正常)，(皮带保护箱:正常)};

E={电机控制箱发生故障，皮带保护箱发生故障，正常停机}=

δ={

if(电机控制箱状况:故障)then(皮带机状态(i):逆停);

if(皮带保护箱状况:故障)then(皮带机状态(i):逆停);

if(皮带机状态(i):运行)&(皮带机状态(i+ 1):顺停or逆停)then(皮带机状态(i):逆停);

if(皮带机状态(i):运行)&(皮带机状态(i-1):顺停|逆停)then(皮带机状态(i):顺停); }。

按照基于规则的系统设计方法，系统包含规则匹配单元和事件处理单元。规则匹配单元包括规则库和工作内存，事件处理单元包括外部事件和内部事件的响应和处理。对象状态消息传入规则匹配区中，首先更新工作内存中存放的对象状态消息，然后进行规则匹配，整个过程结构如图2所示。

图2中，规则库存放用于表示对象状态转换的规则;工作内存存放对象的当前状态，为规则匹配提供依据。发送到规则匹配区的消息先更新工作内存中对象状态，再进行规则匹配。规则匹配过程是将规则与当前工作内存中的对象状态进行比较。以上过程按照实体流图法建模(实体流图法是借鉴程序流程图方法产生设计的)，其过程如图3所示[8]。

对比图2和图3可以发现，产生式规则表示法系统逻辑由规则式描述，系统控制程序主要完成规则匹配和消息的传递，比一般实体流图法的逻辑存在整个控制系统程序中，具有更好的可维护性和可操作性。系统需求变更，系统控制单元不变，只需改变规则库。这样将繁琐的程序逻辑设计转化为类自然语言描述的规则式，方便设计工作。

图2 停机问题基于规则的系统结构图

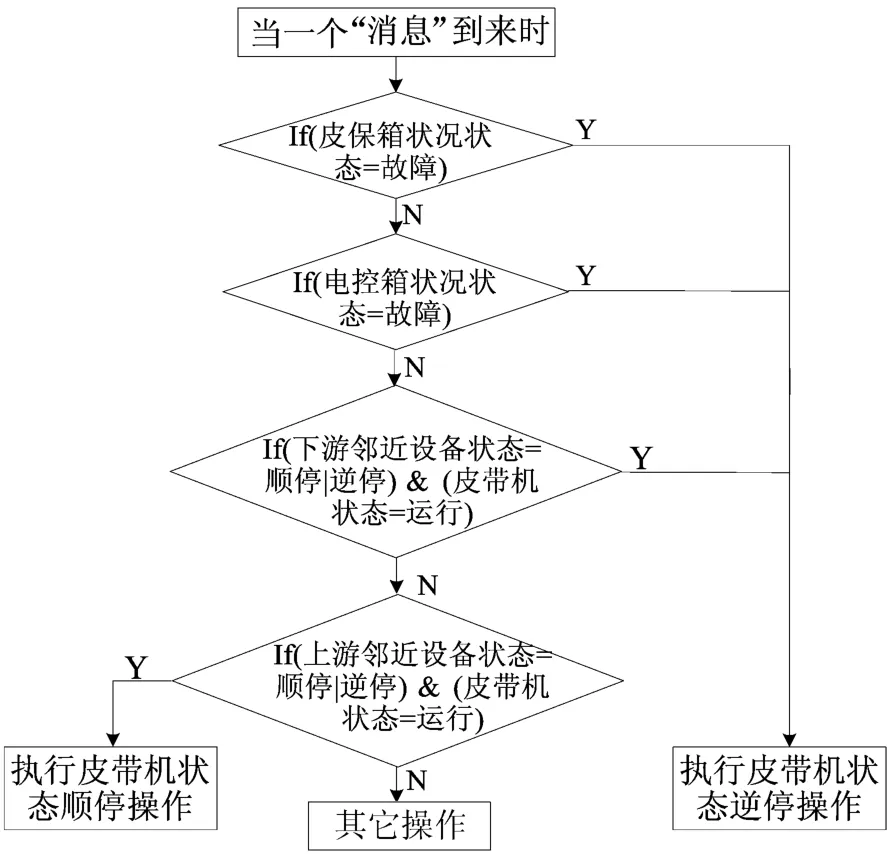
图3 实体流图法系统结构图

2 规则库的结构错误检测

2.1 错误分类

在实际应用过程中，周期性地对规则库进行调整，包括添加、删除、修改操作，可能导致规则库的结构错误。因此在对规则库进行修改后，有必要对规则系统进行有效验证，以保证规则系统的完备性和一致性。同时，还需检测会降低系统运行效率的冗余规则等。

典型的错误包括冗余、不一致、死结点、不可达结点和死循环[6]。

(1)冗余。一个规则系统中，如果2条规则的前提为包含关系，结论相同，则为冗余。

(2)不一致。也称冲突或矛盾，如果在相同的前提下，可以推导出相互矛盾的结论，则称该规则系统是不一致的。

(3)不完备。指规则库对系统的刻画不完整，可能是遗漏了部分规则，分2种情况:①死结点，实体只出现在结论集中，没有出现在前提集中，且不是目标结论;②不可达结点，实体只出现在前提集，没有出现在结论集中，并且不在输入集中。

(4)死循环。在规则系统中，由一个前提出发，通过一系列的逻辑推理，又推导出该前提，使得推理不能正常结束。

2.2 检测方法

(1)冗余。如果2条规则构成冗余，有2个必要条件:2条规则的结论相同;2条规则的前提集合为包含关系。证明略，根据定义可得。

(2)冲突。2条规则是冲突的，当且仅当:2条规则的结论相互冲突;2条规则的前提集合不冲突;任意结论不为对方的前提。

证明如下。

充分性:ri与rj的结论相冲突，如果ri和rj的条件集合不冲突，则在rj与rj的条件合集下，可同时引发ri与rj，使得出现不一致。

必要性:利用反证法可得。如果2条规则的结论不相冲突，则不会不一致;如果2条规则的前提集合相冲突，则不会同时出现在某一前提集下;如果一条件规则的结论是另一条规则的条件，事件的发生有先后顺序，也不会同时出现。

(3)死循环。一组规则构成死循环当且仅当:构成回路，即每条规则的结论都出现在另一条规则的前提中;该组的条件集合减去该组的结论集后，所得集合要么为空，要么不冲突。

证明如下。

充分性:设有规则集合{ri，…，rk}，构成回路，条件集合减去结论集合后所得集合为C，且C内元素不冲突。在ri成立的条件下，把ri的结论放到当前的前题集合中，继续匹配，则可以得到rj，…，rk。又rk的结论为ri的前提，ri再次成立，匹配不能正常结束。

必要性:如果{ri，…，rk}不构成回路，则匹配可以正常结束，不会引起死循环;如果条件集合减去结论集合得到结果集C，所得结果相冲突，假定ri与rj的前提部分出现在结果集C中，则规则ri与rj不会都匹配成功，推理可以正常结束。

(4)完备性。系统的完备性依赖于具体的应用，假定有目标结论集p o，前提集p i。规则库的结论集合Cres，规则库的条件集合Ccon。

根据定义可得:Ccon-Cres-po则为死结点; Cres-Cres-p i则为不可达结论。

2.3 实例分析

限于篇幅，摘取如下规则库片段，LRDL的语义见文献[9]。

r1:[电机控制箱:正常]&[皮带保护箱:正常]==[皮带机状态:运行];

r2:[电机控制箱:故障]==[皮带机状态:逆停];

r3:[皮带保护箱:故障]==[皮带机状态:逆停];

r4:[皮带机状态:运行]&[皮带机状态(i+ 1):逆停|顺停]==[皮带机状态:逆停];

r5:[皮带机状态:运行]&[皮带机状态(i-1):顺停|逆停]==[皮带机状态:顺停];

r6:[皮带机状态:顺停]&[皮带机状态(i+ 1):运行]&[皮带机状态(i-1):顺停]==[皮带机状态:运行];

根据相关定义及定理，得到如下结论:

冗余:无

冲突:{r4，r5}，在前提集{[皮带机状态(i+ 1):逆停]，[皮带机状态(i-1):顺停]}下，可能引起冲突。

不完备:无

死循环:{r5，r6}在前提集{[皮带机状态(i+ 1):运行]，[皮带机状态(i-1):顺停]}下，可能引起死循环。

上例是规则库的第1个版本中的部分规则，经逻辑验证，存在结构错误，经过适当修改，成功通过验证。这也证实了规则库与推理机的相互独立性，给系统的维护带来了方便。

3 结束语

本文研究的离散事件系统的系统结构借鉴专家系统中基于规则系统架构，采用产生式规则描述方法描述系统的事件发生和状态转移;并对得到的规则库进行了有效的结构验证，保证了规则库的内部逻辑的正确性。对规则匹配的算法研究可以参考文献[10]，至于规则库刻画的系统控制逻辑是否合理，有待进一步的仿真实验。

[1] Ouidad K R.Interacting w ith reasoning in a MAS in tegrating a RBS[C]//Information and Communication Technologies，ICTTA 2006，Vol 2，2006:3001-3006.

[2] Campbell A S，Wainer G A.Applying DEVS modeling for discrete eventmultip lem odelcontrol ofa time varying plant [C]//W in ter Simulation Conference，2006:823-831.

[3] 韩江洪，郑淑丽，陆 阳，等.离散事件控制系统规则化描述方法的研究[J].合肥工业大学学报:自然科学版，2005，28 (9):1081-1084.

[4] 曲长征，于永利，金 伟，等.基于ExSpect的复杂离散事件动态系统建模[J].系统仿真学报，2005，17(12): 3011-3013.

[5] 孙 安，毕 翔，韩江洪，等.基于状态转换图的LL语法快速分析方法[J].合肥工业大学学报:自然科学版，2009，32 (7):1030-1033.

[6] 丁志军，潘美芹，蒋昌俊，等.无回路规则系统的Petri网验证方法[J].同济大学学报:自然科学版，2007，35(2): 232-238.

[7] 宋新民，龙杨喜，贾志军.基于仿真的故障诊断专家系统应用研究[J].系统仿真学报，2006，18(4):1038-1040.

[8] 王维平，朱一凡，李 群，等.离散事件系统建模与仿真[M].北京:科学出版社，2007:25-57.

[9] 魏振春，韩江洪，陆 阳，等.一种基于规则的语言的公理主义[J].计算机工程与应用，2008，44(20):86-88.

[10] 韩江洪，张亚琼，魏振春，等.基于规则的离散事件系统建模与规则匹配研究[J].系统仿真学报，2008，20(6): 1394-1396，1419.