合作博弈隐含连通性假设述评

应思思

(中国传媒大学媒体管理学院，北京 100024)

1 引言

随着经济全球化的不断发展，全球大部分国家、地区、产业、企业乃至家庭都被巨大的经济网络连在一起。尤其是信息革命蔓延至经济领域之后，经济活动和经济行为效率都越来越依赖于经济主体之间的各种经济关系网络。新的经济现实使得许多经济学家和社会学家对经济网络和社会关系网络产生兴趣，同时吸引了大批学者讨论与经济网络紧密联系的网络协同、合作和分享现象。一些新的直接研究网络的研究方向开始兴起，如网络经济学、社会网络分析和经济社会学等;与此同时，以讨论联盟合作为主题的合作博弈理论研究也重新得到关注。

在上述背景下，本文从经济系统连通性的视角对合作博弈理论隐含的连通性假设做简单述评，以期为构建一种与主流经济理论相一致的经济网络分析理论提供参考。

首先简单给出经济系统和连通性的描述。经济系统理论把经济社会看作一个大系统。与经济活动密切相关的物流网络、金融网络、信息网络等统称为经济系统的广义中介网络。在广义中介网络中，经济系统的各个经济元之间拥有与网络相应的经济连通性。如两个经济元在物流网络中相连通意味着他们之间可进行物质商品转移，即他们具有物质连通性。

2 合作博弈定义及其刻画

Harsanyi于1966年明确提出的合作博弈定义影响广泛，被沿用至今。他定义，“如果在一个博弈中，义务——协议、承诺、威胁——具有完全约束力并且是可强制执行的，则该博弈称为是合作的。如果义务不可强制执行，即使局中人之间在博弈前可以沟通，此博弈仍称为是非合作的。”［1］可以明显地看出，合作博弈从某种意义上来说是相对于非合作博弈定义的。

实际上，合作博弈的研究最早在博弈论开山之作《博弈论与经济行为》中已经由von Neumann和Morgenstern进行过详细的讨论［2］。在此基础上，Nash详细讨论了非合作博弈［3］。他评论《博弈论与经济行为》“研究了n人合作博弈理论，该理论是基于对博弈各方不同串谋形式形成的分析而建立起来的”。而将其《非合作博弈》一文讨论的“理论建立在没有联盟的基础之上，也就是假定博弈各方独立行动，相互之间没有合作和交流”。

Nash1953年的文章《两人合作博弈》对研究中的“合作”一词进行了解释［4］。“我们假设两个个体可以一起讨论面临的情况，并就一个理性的共同行动计划达成一致，也即达成一个假定具有强制性的协议”。这篇文章也提及合作博弈与非合作博弈的差异。他定义“如果参与人不能以任何方式进行沟通或合作，这样的博弈就称为非合作博弈”，并指出“从某种意义上说，它们正好与合作博弈相反”。

由此可见，合作博弈与非合作博弈的区分是自博弈论发展早期就存在的。诺贝尔经济学奖获得者Aumann在《博弈论手册》第一卷的序言中讨论了两者特征的差异［5］。“非合作博弈集中考察个体的策略选择”，“合作博弈理论则处理集体的可行选择”。“因而非合作博弈理论密切关注定义博弈的详细过程和规则;而合作博弈一般已经从这些规则中抽象出来，只从更一般的描述中研究问题，只明确各种联盟能得到什么样的支付，而不考虑如何得到”。“一个不太恰当的类比是”，两者“就像经济学、生物学和物理学中微观视角和宏观视角的关系”，并且“这两大研究途径之间有着十分密切的联系，他们相互补充相互加强”。

本文主要讨论的合作博弈理论都采用联盟型博弈模型，并且都与策略型博弈密切关联。这里首先给出联盟型博弈和策略型博弈的定义。

定义1(联盟型博弈)一个联盟型博弈是一个有序数对(N，V)。N={1，2，… ，n}代表局中人集合，V:2N→ℝN是一个特征函数，将N的每个子集(称作联盟)S⊆N与一个或几个|N|维实向量对应。

其中，N={1，2，… ，n}中的元素代表单个局中人;参与人集合N的任意子集S⊆N称作联盟。特征函数V在可转移效用情况下是一个实值函数，v(S)∈ℝ此时表示联盟S的所有成员合作时能够获得的总支付，通常在策略型博弈的效用函数ui的基础上通过推导得到。当不存在可转移效用时，特征函数V将联盟S与其效用可能性集V(S)相联系，并要求V(S)是包容的非空闭集，表示联盟S可以获得的所有可能支付的集合。

定义2(策略型博弈)形式上，一个策略型(strategic-form)博弈就是任何一个具有如下形式的系统 Γ［5］:

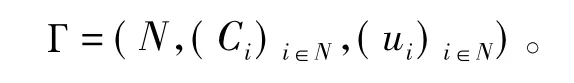
其中N是一个非空集，代表局中人集合，对N中的每一个i，Ci是一个非空集，且ui是从到实数集R的一个函数。这里，N是这个博弈的局中人集。对每个局中人i，Ci是可供局中人i利用的策略(或纯策略)集。在策略型博弈Г进行时，每个局中人i都必须在集中选择一个策略。一个策略组合(strategy profile)就是N中所有局中人可以选择的策略的一个组合。设C是由所有可能的策略组合所组成的集，则:

对于C中任一策略组合 c=(cj)j∈N，如果 c是局中人所执行的策略组合，那么ui(c)就表示此时局中人i在这个博弈中将得到的期望效用支付。

3 合作博弈的联盟假设

在合作博弈中，博弈局中人集N的任何一个非空子集S都可能形成联盟(coalition)。一般地，当我们说一个局中人联盟的成员可以有效地谈判(negotiate effectively)时，我们的意思是，如果联盟成员的策略中存在一个可行的变化能使他们全部受益，那么他们将同意实际做出这样一个变化。除非它与联盟中某些成员与联盟外的其他局中人之间可能形成的协议相矛盾［6］。

由合作博弈定义可知，合作博弈区别于非合作博弈的关键因素在于，合作博弈中存在可有效谈判的联盟。由于联盟的存在，合作博弈的局中人不仅可以采用个人策略，还拥有与其他联盟成员共同实施相关策略的能力。换句话说，在合作博弈中，联盟的成员相对于联盟外的其余局中人而言是相互合作的，而在联盟内部仍需就联盟收益分配进行竞争。本文将合作博弈局中人之间的这种多重策略互动模式称为合作竞争。

在合作博弈的研究文献中，联盟都是讨论的中心。Aumann在比较合作博弈与非合作博弈特征差异时提出，合作博弈处理(联盟)集体的可行选择，其研究的主要内容是“何种联盟会产生?联盟的得益如何分配?”［5］事实上，合作博弈为了集中分析联盟合作，牺牲了非合作博弈中发展的对各种博弈细节的刻画，而将它们抽象为联盟特征函数。从这个意义上说，合作博弈相对于以策略型和扩展型博弈为出发点的非合作博弈有着完全不同的分析视角。这种视角的差异类似于经济学理论中的宏观视角与微观视角的差异。

博弈论研究史上最早对联盟进行讨论和刻画的是 von Neumann和 Morgenstern［2］。他们在《博弈论与经济行为》中讨论了联盟分析所需的基础假设，并首先使用特征函数来刻画联盟。此后，合作博弈研究多以联盟型博弈为基础，由于联盟型博弈以特征函数最为关键，又常被学者称为特征函数型博弈。

从这个角度来说，博弈论文献中已研究的博弈可根据局中人连通性属性的不同大致分为三大类:严格竞争博弈，非合作博弈和非合作博弈。

严格竞争博弈即二人零和博弈，是连通性结构最为简单的博弈经济系统。严格竞争博弈的两个局中人拥有完全对立的支付函数，即ui(ci，cj)=-uj(ci，cj)［7］。这一类博弈的研究为博弈论研究提供了分析的基本概念体系和分析思路。博弈论的早期结论都是关于严格竞争博弈提出的，著名的有泽梅罗定理、冯·诺依曼的最小最大定理等等［8］。

非合作博弈对应着局中人相互竞争但不存在联盟合作的情况，由于不必考虑结盟可能性对策略连通性的约束，这类博弈问题在这个意义上来说仍然比合作博弈简单。非合作博弈中对局中人策略竞争连通性的强调和讨论直接体现在局中人的支付函数形式上:ui=ui(ci，c-i)，其中-i表示N中除去i之外的所有局中人，c-i则表示除i之外所有局中人的策略组合。具体地说，非合作博弈的效用函数意味着局中人i的效用不仅取决于i自己的行动，也同其他所有局中人-i的行为有联系。这也是所有博弈论问题的共同点。因此，非合作博弈实际上在不考虑联盟合作的情况下为一般化的n人博弈问题的探讨提供了恰当的模型起点。当博弈规则转化为二人零和博弈时，非合作博弈的效用函数与严格竞争博弈效用函数有着同样的形式。

相对于严格竞争博弈和非合作博弈来说，合作博弈是对协议约束(必然存在合作结构)下博弈局中人得益进行聚焦的理论。联盟成员间的策略连通性同时具有合作与竞争的双重属性，在涉及的策略连通性方面比上述两种博弈问题都更复杂。合作博弈中出现的这种策略连通性的复杂性源自其经济系统结构上的复杂性，即出现了联盟这一介于局中人和博弈全局之间的中间结构。如果说严格竞争博弈和非合作博弈的分析主要集中于局中人个体分析的层面，那么合作博弈分析则在允许联盟结构存在的情况下将重心聚焦于联盟合作层面。从经济系统的角度来看，这是系统层级的飞跃。

正是联盟的出现，使得合作博弈局中人在与其余所有局中人竞争的同时，还必须面对与哪些局中人合作的决策。从经济系统连通性的角度来看，站在联盟层次对合作进行分析，必须同时考虑所有局中人之间的竞争性策略连通和联盟成员间合作性策略连通。

由上述讨论不难发现，合作博弈较非合作博弈和严格竞争博弈而言拥有更复杂的经济系统层次结构，也相应地存在更复杂的局中人策略连通结构。正如之前提到的，复杂的根源在于合作博弈的联盟层次和与之相应的合作与竞争并存的策略连通格局。因此，合作博弈研究无一例外地聚焦于联盟分析，为此牺牲了博弈中除支付空间外的所有博弈细节，无论是行动顺序、策略集还是信息集都被抽象掉了。这一处理恰与系统经济学的层级战略相契合［9］。层级战略认为，在经济系统中考虑第N层系统的问题，须要在第N+1层系统进行分析。合作博弈研究则正是通过特征函数的推导完成了由第N层到第N+1层的自由度归并，具体推导过程后文将做简单介绍。最终，合作博弈运用特征函数对各种可能出现的联盟情况进行刻画，为联盟层次的博弈分析搭建了合适的平台。

联轴器的玻璃钢中间管是实现联轴器电绝缘的关键部件，玻璃钢中间体制造好后，需要进行绝缘电阻测试，要求玻璃钢中间体两端的绝缘电阻不小于10 MΩ(1 000 V DC)。

事实上，为了保证合作博弈联盟层次的存在和稳定性，合作博弈研究还根据需要对博弈系统的其他连通性进行了合理假设。这些连通性假设的存在使得合作博弈理论更加丰富。

4 合作博弈常用的其他连通性假设条件

(1)相关策略

在联盟型合作博弈中描述联盟，首先需要寻找相应的数学结构来刻画联盟行动以及联盟行动带来的效用。为此，合作博弈需要在非合作博弈语言的基础上发展与联盟相关的假设。最直接和基础的假设就是博弈中联盟成员可通过采取相关策略进行合作。这意味着联盟内部成员之间存在合作策略连通性。

在从策略型博弈导出联盟式博弈的过程中，相关策略的描述是特征函数推导的基础。下面在具可转让支付的假设下给出相关策略的定义。

定义3(相关策略):形式上，给定任一策略型博弈 Г =(N，(Ci)i∈N，(ui)i∈N)，某些局中人组成的集的一个基于纯策略的相关策略(correlated strategy)就是，这些局中人在Г中所能选择的所有纯策略组合集上的任何一个概率分布［6］。也就是说，任给一个S⊆N，S的一个相关策略是，且中的任何一个概率分布，其中

定义4(相关策略期望效用):给定所有局中人在△(Cs)中的任一相关策略μ，对于每个局中人i，令Ui(μ)表示当μ在博弈Г中被执行时局中人i所能得到的期望支付，则有

在相关策略假设的基础上，Myerson(1991)认为，“至少有3种方法可以从n-人策略型博弈中导出合作博弈的特征函数，分别导出3种特征函数表示:最小化最大表示(mini-max representation)、防御均衡表示(defensive-equilibrium representation)和理性威胁表示(rational-threats representation) ”［6］。实际上，所有这三种方法的应用，都需要首先明确相关策略和相关策略对应的局中人期望效用函数的定义和表示。

以特征函数的最小化最大表示为例。给定一个具有可转移效用的策略型博弈(ui)i∈N)，冯·诺依曼和摩根斯特恩［2］提出把特征函数定义为

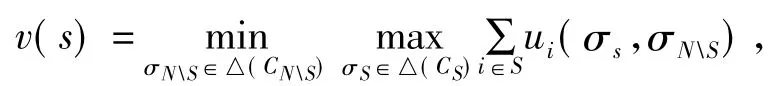
这里的NS表示N中不在联盟S内的所有局中人组成的集。

由此可见前述特征函数定义v(S)是联盟S的成员在对付互补联盟NS的最佳攻击威胁时所能保证得到的最大效用支付和。如果v(S)满足上述式子，我们就称v为具有可转让效用的策略型博弈Γ的联盟型最小化最大表示。

在上面的特征函数推导过程中，相关策略是推导的基本要素。

合作博弈允许联盟成员采取相关策略是针对局中人策略集做出的假定，因此在已经抛弃策略描述的联盟式博弈中不可能得到直接体现，而只能在由策略型博弈诱导的联盟型博弈特征函数的表达式中，通过局中人期望效用的计算间接地显现。

由于相关策略是将联盟中所有成员采用策略进行关联后得到的，其存在内生地在联盟内部搭建起了一种策略中介网络。这使得联盟全体成员具有全局策略连通性，并且这种连通性更接近于联盟全体成员的协调连通。这从相关策略的形式中也可以看出。

表1 相关策略与混合策略组合的比较

因此，相关策略假设实际上意味着所有可形成联盟的成员之间都存在策略的协调连通性，以此强调联盟中存在具有约束力的协议。

(2)可转让效用

在合作博弈联盟型框架中，研究者为了简洁描述博弈所处的特定底层社会或经济情况，常常同时采用可转让效用(transferable utility，简称TU)和附加支付(side payment，简称SP)这两个假设条件，以构建符合要求的效用理论。采用这种假设的联盟式合作博弈吸引了众多合作博弈研究者，这类博弈的研究也拥有了相对于其他合作博弈而言更为丰富的文献和正式结论，因而在合作博弈研究中占据重要地位。我们通常将同时运用TU和SP假设的合作博弈称作具有可转让效用的博弈(TU games)或者具附加支付或旁支付的博弈(games with side payment);而将不采用这两个假设的合作博弈称作不具可转让效用博弈(games without transferable utility)或者不具附加支付(或旁支付)的博弈(games without side payment)。本文主要分析TU博弈，借此对TU和SP假设作简要述评。

前面已经给出TU博弈的定义，也曾讨论由策略型博弈诱导的TU博弈特征函数。由其特征函数形式v(S):2N→ℝ可知，TU博弈仅用一个实数就概述了某个联盟的可得结果，即联盟可达到的总支付。为使该特征函数v(S)有意义，TU和SP缺一不可。

SP简单指博弈除去规则内生的任何支付之外，允许进行附加支付。

TU则在SP的基础上，假定存在一种无限可分且承载着效用的合意商品(一般等价物，比如货币)，作为联盟型博弈特征函数的测度单位，并且每一单位该种商品的转移都会带来转出者一单位效用的减少和接受者一单位效用的增加。因此效用可通过该种商品的流通而在局中人之间无损失地转移。这一情况也被称作效用是“无条件转移(unrestrictedly transferable)”的。

需要注意的是，可转让效用这个术语并不意味着效用可以直接在两个局中人间转移。效用作为一个派生概念是附着于商品之上的，不可能直接转移，而只能通过商品的转移而改变相关局中人的效用水平。而这种效用水平一增一减的现象，可以形象地看作效用在发生转移，从效用减少的一方转移到了效用增加的另一方。

根据冯·诺依曼和摩根斯特恩［2］，一个具有TU和SP的联盟型合作博弈定义如下。

定义5(TU博弈)二元组(N，v)是一个具可转移支付的联盟式合作博弈(a cooperative game in characteristic function form with transferable utilities)，如果N是一个有限的参与人集合，V:2N→ℝ是一个特征函数，它将联盟可获得的最大收益v(S)赋予每一个联盟S⊂N，且满足v(Ø)=0。

其中v(N)表示博弈中所有参与人集体(大联盟)创造的总财富。而价值的分配就是一个支付向量 x∈ℝn，它满足。

一般的n人联盟型合作博弈在博弈情况的刻画问题上有着极大的复杂性。为了最大程度地简化可能出现的联盟情况，研究者们希望通过假设得到联盟总得益的惟一测度，并将其作为特定联盟博弈的特征函数值。TU和SP的同时使用能够充分达到这个效果。

如前面提到的，TU与SP允许联盟总得益可在联盟成员内部任意分配。这令联盟可得的最大总支付作为一个实值量有意义且惟一，尽管略去了同一联盟中成员得益分配可能出现的差异。

然而达到方便联盟分析目的的同时，这些假设仍有着内在的特定局限性。有文献提出SP假设可能改变原有博弈的解［13］，因为它的存在大大强化了联盟成员间的策略连通性，进而强化了某些联盟出现的可能性。冯·诺依曼和摩根斯特恩在初次使用SP时就对于这种影响进行了详细描述［2］。

而TU在20世纪60年代也被证明是相当严格的条件，因为它实际上要求联盟内所有成员对于货币的效用函数都是拟线性的，即博弈局中人的偏好必须采用基数效用函数表示。这一点可以从具有TU的策略博弈效用函数Ui(cs)=ui(cs)+x中看出。

这在经济学理论术语中称为“拟线性效用加假设”，该假设条件下意味着联系不同市场的收入效应不存在。因此如果在市场博弈中采用TU假设，该博弈只能描述市场的局部均衡情况，无法同时讨论多个市场。这使得TU博弈无法完整描述大型经济的一般均衡情况。

鉴于SP和TU内在的这些局限性，Aumann和Peleg同时抛弃了TU和SP，在NTU博弈基础上发展了联盟式博弈的概念体系和部分解概念［11］［12］。NTU博弈此后被普遍应用于大型市场博弈分析。

在由博弈诱导的经济系统框架中，TU和SP假设意味着在原有局中人得益空间基础上并上一个“货币-效用流通”空间。这是一个对应于局中人集的货币资源分布空间，而在这个空间里，每一对局中人的对应货币资源点之间都存在着连通性。即存在一族作用gkij:X2→X2，对于任意选择的i和j属于联盟 S，满足，其中 kij满足

这样，我们就得到一个定义在联盟S上的封闭但具有全局连通性的货币资源空间，空间中的货币总量守恒。于是联盟总效用必然有上确界，即该联盟所能得到的最高得益总量，可用于概述联盟的效用特征。

正是因为SP和TU的存在，我们可以推断联盟型合作博弈中隐含的效用连通性状况。也正是这种理想化的连通性假设，在与之相关的大量文献中达到有效描述某种现实经济状态(如市场博弈)的目的的同时，充分证明连通性结构会对经济系统产生重要影响。

(3)超可加性

基于联盟式合作博弈的研究还常常假设特征函数v或V拥有分别定义的超可加性。事实上1944年冯·诺依曼和摩根斯特恩就在讨论一般非零和博弈的特征函数时提到，他们提出的特征函数具有超可加性［2］。这是关于特征函数可加性的最早论述。

接下来简要介绍在TU和SP条件下联盟式博弈特征函数的超可加性假设和来自连通性视角的可加性解读。首先给出特征函数的超可加性的定义。

定义6(特征函数的超可加性)给定联盟型博弈Г=(N，v)，当且仅当每一对属于N的联盟S和T都满足命题“如果 S∩T=Ø，则 v(S∪T)≥v(S)+v(T)”，称特征函数v是超可加的(super-additive)，并称博弈(N，v)是超可加博弈。

由定义可知，在超可加博弈中，不相交联盟间的合并必然增加他们的特征函数值。可以证明，如果v是前文介绍过的策略型博弈的最大最小化表示，则v一定是超可加的。其他表示则不一定。

还需要注意的是，对于任意一个联盟型博弈，我们都能通过“超可加覆盖”［6］定义一个与之相应的超可加博弈。这令超可加性假设拥有了更广泛的应用空间。

正如前面所介绍的，超可加性意味着超可加博弈中任何不相交联盟进行联合行动的价值至少与他们各自行动的价值一样大。许多学者运用超可加性假设来达到大联盟N最终形成的状态。Hart和Kurz对此写道:“我们设社会作为一个整体是有效地运转的，并将其作为一个假定;我们要设法解决的问题是收益是如何在成员中分配的。带着这样的视角，联盟并非是为了成员获得他们的价值后离开博弈而形成的。相反，他们将留在博弈中作为一个联合体与其他所有局中人谈判。［14］”这也可以视作是对合作博弈定义所强调的“存在具有约束力的协议”的一种诠释。

图1 联盟S形成时局中人合作连通性示意图

需要注意的是，Hart和Kurz将超可加性解释为假定社会运作是有效的［14］。这种解释同经济系统框架中涉及的基于连通性的“有效”概念是一致的。连通性视角下，经济系统由硬部和软部两大部分组成，而连通性就是因软部而存在的。在TU和SP条件下的联盟型合作博弈也可以被视作一个经济系统，其中局中人和联盟就是系统的经济元，属于硬部，而他们之间的各种联系都属于软部。在这个系统中，TU和SP共同描述了经济元(局中人和联盟)效用空间上的连通性状况。在这种解释下，超可加性描述的实际上是经济系统得以维系的系统经济条件，即“整体大于部分之和”。而整体较部分之和多出的部分就是前面所说的软部，即提供各种连通性的部分，或者也可以说整体价值与部分价值之和的差值都是软部的贡献。

从这个意义上来说，具有TU和SP假设的联盟式超可加博弈与经济系统框架实际上是对类似经济状态的不同描绘。而在由这类博弈所诱导出的对应经济系统中，连通性存在的原因相对清晰，特定连通性带来的价值也能得到定量的测度。图1至图3大致描述了超可加性博弈可能形成的联盟S、T和S∪T与它们形成时的局中人合作连通性情况。

如果将超可加性的判定表达式v(S∩T)≥v(S)+v(T)进行改写，可得到不等式v(S∩T)-v(S)-v(T)≥0。

不等式左边就可以作为连通性价值的度量，而这个超可加性判定式则意味着超可加博弈中连通性价值必然非负。这显然与经济系统的维系条件相一致。因此超可加性如果被解释为假定社会是有效运作的，其中的有效概念也与经济系统中的“系统经济”这一效率概念一致。

5 小结

经过简单的评述，我们从经济系统连通性的角度对合作博弈中涉及的几种连通性假设进行了讨论。其中最重要的是联盟内部连通性假设，这一假设实际上是通过相关策略、TU与SP以及超可加性等常用假设来保证的。在此基础上，我们找到一种与经济系统模型相一致的合作博弈，他们同时满足上面提到的所有假定。文中详细讨论了其中最典型的一类，即由策略博弈诱导的联盟型博弈。可以肯定，这类博弈可以方便地表示为一个拥有完全货币-效用连通性的有效运作的经济系统。这为发展一套能够刻画经济网络的经济系统模型提供了一个可能的起点。

［1］ Harsanyij C.A general theory of rational behavior in game situations［J］.Econometrica，1966，34(3):613–634.

［2］ Vonneumann J，Morgenstnrn O.Theory of games and Economic Behavior［M］.Princeton:Princeton University Press NJ，1944.

［3］ Nash J F.Non-cooperative games［J］.Annals of Mathematics，1951，54(2):286-295.

［4］ Nash J F.Two-person cooperative games［J］.Econometrica，1953，21(1):128-140.

［5］ Aumann R J，Hart S(Eds).Handbook of game theory with economic applicationsⅠ［M］.Amsterdam:Elsevier Science Publishers(North-Holland)，1992.

［6］ ［美］罗杰·B迈尔森.博弈论:矛盾冲突分析［M］.北京:中国经济出版，2001.

［7］ 高红伟，［俄］彼得罗相.动态合作博弈［M］.北京:科学出版社，2009.

［8］ Aumann R J.Game theory.［M］//Eatwell J，Milgate M，New-man P，(Eds.).New Pal grave Dictionary of Economics.London:Macmillan，1987(4):460-482.

［9］ 昝廷全.系统管理模式［CD］.北京:北京广播学院电子音像出版社，2005.

［10］ Weber R J.Games in Coalitional Form［M］//Aumann R J，Hart S，(Eds).Handbook of Game Theory with Economic Application，1992(2):1285-1303.

［11］ Luce R D，Raiffa H.Games and Decisions［M］.New York:Wiley，1957.

［12］ Aumann R J，Peleg B.Von Neumann-Morgenstern solutions to cooperative games without side-payments［J］.Bulletin of the American Mathematical Society，1960(66):173-179.

［13］ Kaneko M，Wooders M H.Utility theories in cooperative games［M］.Barberas，Hammond P J，Seidl C，(Eds).Handbook of Utility Theory:Extensions.Boston:Kluwer Academic Publishers，2004:1064-1098.

［14］ Hart S，Kruz M.Endogenous formation of coalitions［J］.Econometrica，1983(51):1047-1064.