Haynes230高温合金的静态再结晶动力学

彭聪辉， 常 辉， 胡 锐， 樊江昆， 柏广海， 傅恒志

(西北工业大学凝固技术国家重点实验室，西安710072)

Haynes230高温合金是美国20世纪80年代初研制成功的Ni-Cr-W系高温合金［1］，具有良好的高温强度、优良的抗氧化性和耐腐蚀性，以及较好的热稳定性［2］，已应用于航空、航天及核工业领域［3］。除了以板状、棒状以及涡轮盘状得到应用外，Haynes230高温合金正逐步应用于一些形状复杂件或薄壁件的制造中［4，5］。针对复杂零件成形问题，通常采用等温塑性成形方法实现高温合金件的精确成形［6］。等温塑性成形要求变形前的合金晶粒组织均匀、细小，从而使其变形抗力减小，实现精确成形［7］。

Shiomi Kikuchi［8］等人通过粉末冶金法制备了IN-100细晶高温合金，组织细化是在合金制备过程中完成的。王淑云［9］等人采用等温锻造变形对FGH96高温合金进行细晶处理，得到一种没有完全再结晶的变形态组织，宏观晶粒轮廓仍较为粗大。L Ceschini，HongJun Lv等人［10，11］研究了 INCONEL718合金的晶粒细化工艺，利用基体中析出均匀弥散的δ相钉扎晶界，来控制再结晶后晶粒尺寸。然而Haynes230高温合金为固溶强化型高温合金，基体为单一的奥氏体相，故上述工艺均不适用于该合金的组织细化。针对Haynes230高温合金，可以通过调整冷变形量及控制静态再结晶来细化晶粒，使其形成理想的细晶组织，从而改善合金高温塑性成形能力。本研究从经典再结晶理论出发，对冷轧Haynes230高温合金的静态再结晶行为进行研究，计算得到再结晶激活能及动力学曲线，为实现Haynes230高温合金的组织细化提供理论指导。

1 实验方法

实验材料为美国哈氏公司生产的退火态Haynes230高温合金板材，其主要化学成分如表1所示。板材尺寸为20mm×20mm×10mm，在双辊轧机上进行冷轧，变形量为20.5%，29.1%，39.7%，49.8%;对冷轧板材进行再结晶退火，退火温度：1100℃，1125℃，1150℃，1175℃，1200℃;保温时间：10min，20min，30min，40min，60min。沿试样轧制平面进行机械研磨和抛光，用盐酸与硝酸混合溶液(3∶1)进行腐蚀，用OLYMPUS/GX51型光学电子显微镜对其显微组织进行观察。采用直线截距法测量平均晶粒度［12］，通过金相网格法对显微组织进行定量分析［13］。

2 结果及分析

2.1 冷轧+再结晶退火后的显微组织及其分析

图1为Haynes230高温合金经20.5%变形量冷轧后在1100℃保温不同时间的显微组织。可以看出，保温时间为10min时，合金组织没有发生明显变化，原始晶粒晶界处形成少量细小的再结晶晶粒。随着保温时间的延长，细小的再结晶晶粒逐渐增多。

表1 Haynes230合金的主要化学成分(质量分数/%)Table 1 Main chemical composition of Haynes230(mass fraction/%)

保温至60min后，再结晶过程基本完成。另外，试样经室温冷轧及退火后，显微组织中出现了较多的孪晶，这是因为Haynes230高温合金具有较低的层错能，低层错能不仅会阻止试样在变形过程中位错的交滑移，同时也降低孪晶界的界面能，促使在位错开动之前金属所受应力已达到孪生变形所需应力。

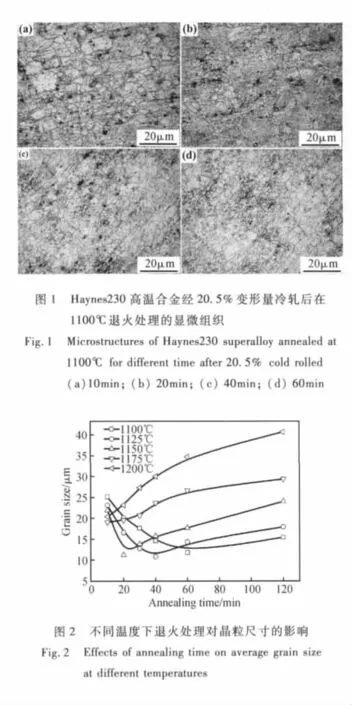
Haynes230高温合金经20.5%冷轧变形并在不同温度下保温过程中晶粒尺寸与退火时间的关系见图2。可以看出，在1100～1150℃退火时，保温时间从10min延长至120min，晶粒尺寸呈先减小后增大的变化过程，这说明在较低温度下再结晶过程较为缓慢，随着再结晶的进行，晶粒逐渐变小，再结晶完成后，晶粒逐渐长大。Haynes230高温合金在1125℃保温至 40min左右时，晶粒尺寸最小，为11.17μm。在1150℃下保温20min时，晶粒尺寸比1125℃下保温相同时间小，说明在1150℃下20min内形成的再结晶晶粒多于1125℃。随着保温时间的延长，保温相同时间下1150℃的晶粒尺寸比1125℃大，说明1150℃下再结晶晶粒长大的速率较大。当退火温度高于 1175℃时，保温时间大于10min后，晶粒始终在长大，说明在此温度范围内再结晶完成的时间较短。图3分别为合金经20.5%变形量冷轧后在1125℃，1150℃，1175℃，1200℃下保温60min的微观组织，可以看出冷轧Haynes230高温合金板材在1100～1150℃进行退火，可获得完全再结晶组织，晶粒细小均匀。

图3 Haynes230高温合金在不同温度下退火60min的显微组织Fig.3 Microstructures of annealed Haynes230 superalloy at different temperatures for 60min (a)1125℃; (b)1150℃;(c)1175℃;(d)1200℃

2.2 静态再结晶动力学方程

初次再结晶是通过再结晶晶核的形成及其生长来完成的，这一过程受到形核率和线生长速率的影响。Avirami［14～16］于1941提出了用于描述再结晶过程动力学的JMAK方程，对其两边取对数，可得：

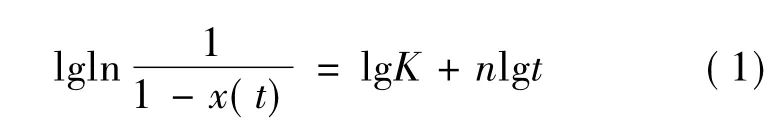
式中x(t)为再结晶体积分数，K为常数，t为保温时间，该式表明lgln{1/［1-x(t)］}与lnt之间具有线性关系。不同冷轧变形的Haynes230高温合金在1100℃下保温过程中时间与再结晶晶粒体积分数关系见表2，将t与x(t)带入式(1)，可以得到不同变形量下在1100℃保温过程中lgln{1/［1-x(t)］}-lnt图(图4)，显然，该图具有较好的线性关系，说明采用JMAK方程可以较好的描述冷轧Haynes230高温合金板材退火处理的静态再结晶过程。将实验数据经过最小二乘法拟合可得到其拟合方程，如图4中所示。

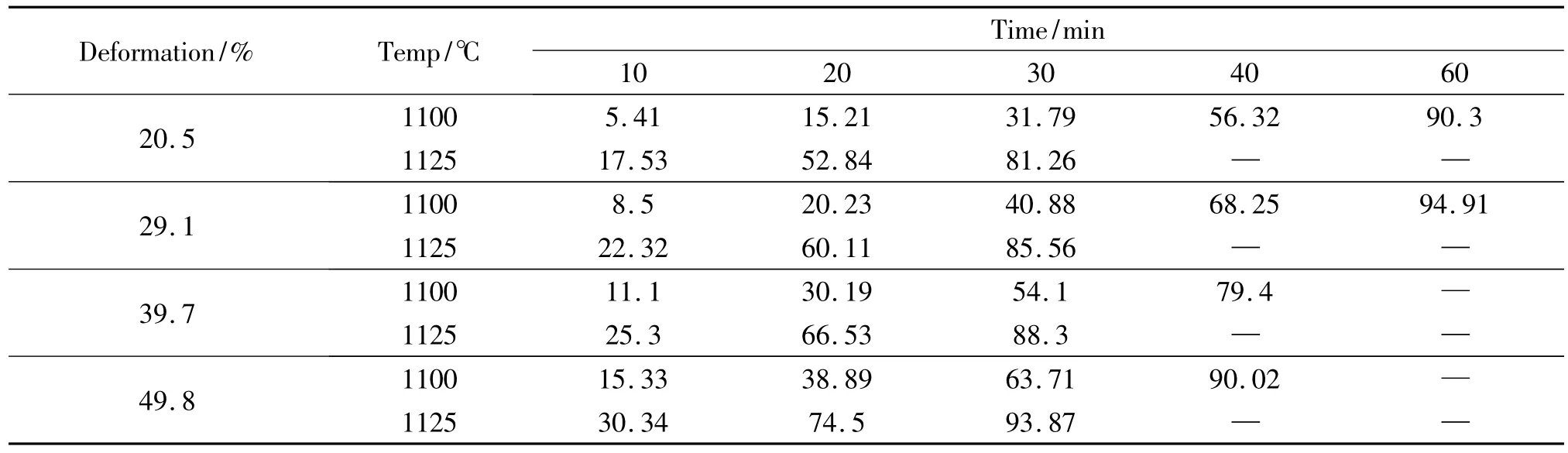
表2 不同变形量下1100℃和1125℃不同时间退火处理后的再结晶体积分数Table 2 Fraction of recrystal grains of Haynes230 alloy at 1100℃ and 1125℃ for different time after different deformation(%)

2.3 再结晶激活能与动力学曲线

再结晶过程中主要包括再结晶的形核和再结晶晶粒的长大两个部分，二者的激活能基本相等，故可用Q统一表示再结晶激活能。再结晶速率与温度的关系可按Arrhenius方程来确定，当再结晶晶粒体积分数一定时，再结晶速率与产生一定量再结晶晶粒体积分数所需时间t成反比，退火时间与激活能之间的关系为：

由不同温度下完成相同再结晶晶粒体积分数所需时间的比值就可以得到材料的再结晶激活能：

参照表2中合金在1125℃保温10min，20min，30min时的再结晶晶粒体积分数，由不同变形量的动力学方程(见图4)分别计算出合金在1100℃保温时20.5%，29.1%，39.7%和49.8%四个变形量下完成相应再结晶晶粒体积分数所需的时间。由式(3)可计算出其再结晶激活能依次为402.50～440.37kJ/mol，362.49～388.56kJ/mol，331.05～340.10 kJ/mol和299.41～318.35 kJ/mol。可以看出，随着变形量的增加，再结晶激活能逐渐减小。这是因为再结晶晶核优先在晶界的位错、空位等缺陷处形成。变形量越大，位错、空位数量越多，一方面为合金再结晶提供更多有利的形核位置，另一方面，位错、空位等结构缺陷处原子引力较低，使再结晶时克服原子引力所消耗的能量减小，从而降低再结晶激活能。

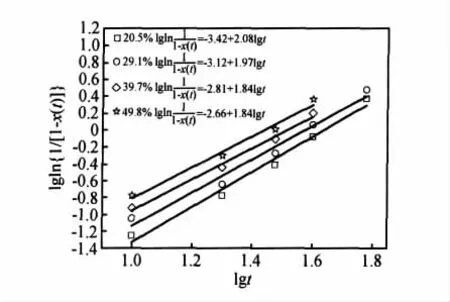
图4 不同变形量下1100℃再结晶lgln{1/［1-x(t)］}-lnt曲线Fig.4 Curves of lgln{1/［1-x(t)］}-lnt at 1100℃and different deformation

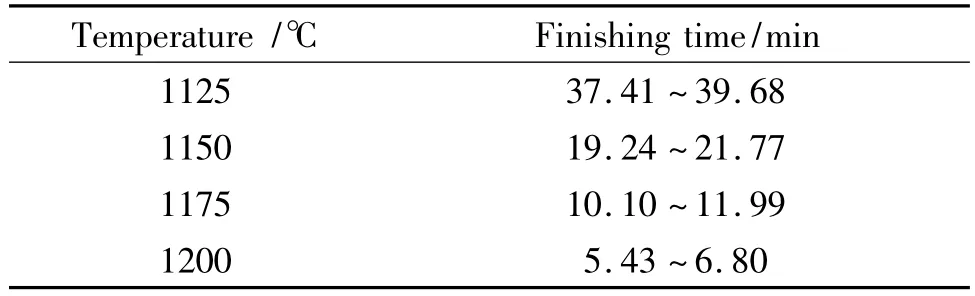
表3 20.5%变形量下再结晶完成时间与温度的关系Table 3 Relationship between time for recrystallization accomplishment and annealing temperature at deformation of 20.5%

按照再结晶完成温度的定义，将再结晶完成时间定义为再结晶晶粒体积分数达到总体的95%，由动力学方程(见图4)可得到合金经20.5%冷轧变形后在 1100℃退火时完成再结晶的时间为74.51min，带入式(3)可计算得到1125℃，1150℃，1175℃和1200℃下保温时再结晶完成时间(见表3)。根据图2，实验结果表明，合金经20.5%冷轧变形后在1125℃保温时再结晶完成时间范围为35～45min，1150℃时为 15～25min，1175℃以上均在10min以内，对照表3，可知计算结果基本符合实验结果。根据式(3)，取20.5%变形量下Q均值为419.462kJ/mol，可以计算得到各温度下的再结晶动力学曲线如图5a所示。根据动力学方程可得到1100℃下不同变形量时再结晶动力学曲线如图5b所示。由图可以看出，相同变形量下，随着退火温度的升高，再结晶形核孕育时间变化不明显，但完成再结晶所用时间急剧减少，这是由于温度越高，原子活性越大，其扩散速率越快的缘故;相同温度下退火，随着变形量从20.5%增大至49.8%，再结晶孕育期变化同样不明显，再结晶完成时间逐渐减少。如果继续增加变形量，一方面增加储存能及形核位置，另一方面降低再结晶激活能，这都有助于热激活过程的顺利进行，从而降低合金初次再结晶温度。

退火温度较低时(1100～1150℃)，再结晶开始时的速率较小，随着退火时间的增加而逐渐加快，再结晶体积分数为20%～70%时，速率最大，然后又逐渐减缓，直至再结晶结束。而在较高温度下退火时(1175～1200℃)，再结晶速率较快，在10min内就基本完成再结晶。

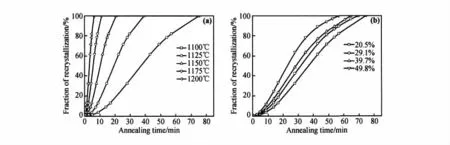
图5 Haynes 230高温合金再结晶动力学曲线Fig.5 Recrystallization kinetic curves of Haynes 230 superalloy (a)20.5%deformation degree at different temperatures; (b)1100℃ temperature at different deformation degrees

3 结论

(1)冷轧Haynes230高温合金板材在1100～1150℃范围内进行退火，可获得完全再结晶组织，晶粒细小均匀。

(2)冷轧Haynes230高温合金静态再结晶晶粒体积分数与保温时间的关系可用JMAK方程进行描述，结合实验数据，计算得到当合金变形量为20.5%，29.1%，39.7%和49.8%时，该合金的再结晶激活能分别为402.5～440.371kJ/mol，362.494～388.557kJ/mol，331.054～340.102kJ/mol和299.41～318.35 kJ/mol，加大变形量可降低合金再结晶激活能。

(3)当合金变形量为20.5%时，由其再结晶激活能计算得到在1100℃，1125℃，1150℃，1175℃和1200℃下再结晶完成时间分别为74.5min，37.41～39.68min，10.1～11.99min和5.43～6.8min，再结晶速率随温度的升高迅速增大。

［1］KLARSTROM D L.Oxidation-resistant nickel alloy：US，4476091［P/OL］.1982.［2010-8-26］.http：//www. wikipatents.com/US-Patent-4476091/oxidation-resistantnickel-alloy.

［2］Haynes International.Haynes 230 Alloy Brochure：No.H-3000［EB/OL］.［2010-8-26］.http：//www.haynesintl.com.

［3］KLARSTROM D L，HOBACK G L，ISHWAR V R.Rejuvenation heat treatment and weld repairability studies of Haynes230 alloy［D］.Munich：University of Munich，2000：34-35.

［4］POP D，WOLSKI K.Surface segregation in Haynes 230 alloy［J］.Appl surf Sci，2006，253：2244.

［5］KLARSTROM D L.Proceedings of the Symposium on Materials Design Approaches and Experiences［C］∥TMS Fall Meeting：Indianapolis，IN，USA，4-8 November，2001：297-307.

［6］吴诗惇.金属超塑性变性理论［M］.北京：国防工业出版社，1997：5-7.

［7］毛卫民，赵新兵.金属的再结晶与晶粒长大［M］.北京：冶金工业出版社，1994：56-68.

［8］KIKUCHI Shiomi，ANDO Shousaku，FUTAMI Shu，et al. Superplastic deformation and microstructure evolution in PM IN-100 superalloy［J］.Journal of Materials Science：1990，25(11)：4712-4716.

［9］王淑云，李惠曲，杨洪涛，等.粉末高温合金超塑性等温锻造技术研究［J］.航空材料学报，2007，27(5)：30-33.

［10］CESCHINI L，CAMMAROTA G P，GARAGNANI G L，et al.Microstructrual refinement and superplasticity of IN-718 superalloy［J］.Journal De Physique IV：Colloque C7，Supplement au Journal de PhysiqueⅢ，1993，3(11)：325-327.

［11］LU Hong-jun，JIA Xin-chao，ZHANG Kai-feng.Finegrained pretreatment process and superplasticity for INCONEL718 superalloy［J］.Materials Science and Engineering A：2002，(26)3：382-385.

［12］GB/T 6394—2002.金属平均晶粒度测定方法［S］.北京：中国标准出版社.

［13］黄启今.通用软件MICROSOFT WORD在显微组织定量分析中的应用［J］.中国体视学与图像分析，2002，7 (3)：182.

［14］AVRAMI M.Kinetics of phase changeⅠ—General theory［J］.Journal of Chemical Physics，1939，7：1103-1112.

［15］AVRAMI M.Kinetics of phase changeⅡ—Transformation time relations for random distribution of nuclei［J］.Journal of Chemical Physics，1940，8：212-224.

［16］AVRAMI M.Kinetics of phase changeⅢ—Granulation，phase change，and microstructure［J］.Journal of Chemical Physics，1941，9：177-178.