B2-NiAl弹性性质Ag合金化效应的理论研究

陈 律，文 韬

(空军航空维修技术学院，长沙410124)

B2结构的NiAl金属间化合物具有熔点高、密度低、强度高、热导率大、抗氧化性好等优异的物理和力学性能，作为高温结构材料，其应用却受到室温塑性较差的限制。合金化可以改变这种金属间化合物的电子结构、结合键类型与强度以及长程有序化的程度等［1］，被证明是一种可有效改善其力学性能的方法［2，3］。研究人员根据合金元素在NiAl化合物中的作用行为，将其分成三类［4］：A类元素Ti，Zr，Hf，Nb和Ta在NiAl中的固溶度很低，常以Heusler相(Ni2AlX)和Laves相(NiAlX)三元金属间化合物形式存在，显著提高NiAl合金的蠕变强度;B类元素V，Cr，Mo，W与NiAl形成伪二元共晶系，共晶组织改善NiAl合金的室温韧性;C类元素Fe，Co，Cu在NiAl中有很高的固溶度，大量加入NiAl合金中，形成塑性第二相而提高其室温塑性。最近周健等人［4］研究了Ag对NiAl合金显微组织和压缩性能的影响，其结果表明Ag合金化能显著提高NiAl合金的室温压缩塑性，而合金元素Ag在NiAl中的作用行为还不清楚。1992年Darolia等人［5］率先发现在NiAl单晶中加入 0.25%的 Fe可使 NiAl在＜110＞方向延展性从1%提高到6%，而Fe的加入量超过0.5%时韧化作用呈消失的变化趋势。Munroe等人［6］进一步指出高浓度Fe合金化不能改善NiAl合金的延性。由此可见，合金元素的浓度对合金化效应有很大的影响。

由于实验条件的复杂性和实验手段的限制，研究者一直没有研究清楚合金化元素Ag对NiAl合金的作用机制。第一性原理计算由于能从丰富的原子尺度信息解释许多实验现象而广泛地应用于金属间化合物的各种物理、力学性质与合金化效应的研究［7～11］。为了更好地理解元素Ag及其浓度对NiAl合金的作用机制，本工作采用第一性原理计算方法系统地研究不同浓度Ag合金化NiAl合金的弹性性质，以期从原子尺度解释合金化元素Ag对NiAl合金的作用机制。

1 计算模型与方法

B2-NiAl晶体结构如图1a所示，Ni原子占据8个顶角位置，Al占据体心位置，它的空间群为pm 3 m，可看成是由两个简单立方子晶格相互交错穿插而成。图1b是16个原子组成的2×2×2无缺陷NiAl晶体超胞模型，图1c，d分别是NiAl晶体Ni空位和Ni反位超胞模型。由于Ag在NiAl晶体中优先占据Ni原子位［12］，并且Ag在NiAl中的固溶度小于1%［13］。因此本工作针对Ni原子位进行了不同浓度(0～1%)的Ag合金化的模型计算。

计算程序为Castep(Cambridge Serial Total Energy Package)总能计算软件包。Castep是基于密度泛函理论的第一原理赝势平面波方法［14］，晶体波函数由平面波基组展开，势函数采用倒易空间表述的超软(Ultrasoft)赝势［15］，交换关联能函数采用GGA中的PBE关系式［16，17］。采用周期性边界条件，平面波数目由动能截断点决定，本计算中所有超胞模型的动能截断点均取330.0eV。根据对称性，超胞模型计算的K点网格数取4×4×4。各项计算之前，都用BFGS方法［18］对超胞结构进行几何优化，以求得其局域最稳定结构。使用基集修正［19］，自洽场计算(SCF)时应用Pulay密度混合法 ，体系总能量收敛值取1.0×10-3eV/atom，每个原子上的力要求低于0.01eV/nm，公差偏移小于5×10-4nm，应力偏差小于0.2GPa。

合金化时势函数采用VCA(Virtual crystal approximation)虚拟晶体近似［21］。VCA近似的主要假设是混合原子的虚拟势可由单原子势与其权重乘积的代数和来表示。该近似已被广泛地应用于无序体系和固溶体结构性质的计算，并被证实可有效地计算晶体的某些结构性质，如 Ramer等人［22］对 Pb (Zr1-xTix)O3晶格常数的计算，计算结果与实验数据一致，Souvatzis等人［21］分别用VCA方法和超胞模型计算了 W0.5Re0.5合金的弹性模量，相对误差＜5%。

图1 计算模型 (a)NiAl晶体结构;(b)Ni8Al8超胞;(c)Ni空位超胞;(d)Ni反位超胞Fig.1 Models of calculation (a)crystal structure of B2-NiAl;(b)Ni8Al8supercell; (c)NiAl supercell with Ni vacancy defect;(d)NiAl supercell with Ni anti-site defect

2 计算结果与讨论

2.1 B2-NiAl晶体的基本物性

首先计算了B2-NiAl晶体的晶格常数a、合金形成热ΔH与弹性模量Cij，结果列于表1，并与先前的实验数据［23～25］，以及Farkas等人［26］、Voter等人［27］和Rao等人［28］的计算结果进行比较。从表1可见，计算结果与实验数据比较接近，之所以存在一定的差距，初步确定其原因在于实验条件下NiAl单晶中杂质原子、热空位、组分缺陷、晶体取向、表面处理、预变形等因素对NiAl单晶本征物理性质的影响较大。计算结果与其他研究中的计算结果接近，表明本工作所选计算条件与参数基本合适。

表1 B2-NiAl的晶格常数a、形成热ΔH和弹性常数CijTable 1 The lattice constant a，the heat of formation ΔH and elastic constant Cijof B2-NiAl crystal

2.2 Ag合金化NiAl晶体的弹性性质

基于图1b的超胞模型，本工作计算了低浓度Ag合金化NiAl单晶的弹性常数。考虑到单晶弹性常数能被用来估算多晶材料的一些弹性性质［29］，进一步采用式(1)～(3)计算了B2-NiAl多晶材料的体模量B0、剪切模量G、弹性模量E［30］。

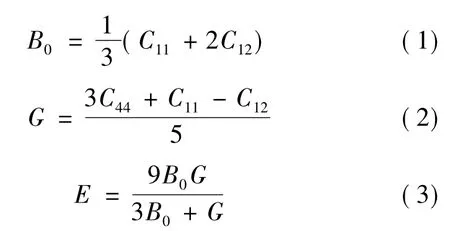
由于材料硬度与弹性模量E和剪切模量G密切相关［30］，虽然不同材料的硬度与其弹性模量的关系不尽相同，但一般来说，E与G的值越大，则材料硬度越高。按照Jhi等人［29］最近的观点，材料的硬度还与弹性常数C44存在单调对应关系，即C44越大，材料硬度越高。这样，通过式(2)与式(3)以及独立变量C44的计算值，图2示出了Ag合金化浓度x对NiAl多晶材料硬度的影响。由图2可知，随着Ag合金化浓度从0增加到1%，B2-NiAl晶体的C44，E，G大幅提高。可见，Ag合金化可显著提高NiAl晶体的硬度，这种效应归因于低浓度Ag的固溶强化［4］。

图3为B2-(Ni1-xAgx)Al单晶Cauchy压力C12-C44与多晶G/B0比值随Ag合金化浓度x变化曲线。基于Pugh等人［31］的经验判据，即：G/B0值越大，材料越脆，反之，延性越好，特别是考虑到这一判据在分析金属间化合物延性或脆性方面的应用可靠性［32］，本工作对图3中G/B0随Ag合金化浓度变化的曲线进行了分析。由图3可见，Ag合金化浓度在0～0.6%以及0.7% ～1%区间，G/B0值相对于未合金化时都要小，说明在上述两个合金化浓度区间Ag有利于NiAl晶体材料延性的提高，浓度在0.6%左右时效果最好。

考虑到Cauchy压力已被很好地用来表征和评判纯Ni和纯Al晶体的延展性以及半导体Si晶体的脆性［33］，即：金属键的Cauchy压力值为正，并且数值越大表示金属键越强、材料的延展性越好;而对于具有强方向性的共价键，Cauchy压力值为负，材料表现为脆性。据此进一步对图3中Cauchy压力C12-C44随Ag合金化浓度变化曲线进行了分析。由图3可见，未合金化时，Cauchy压力值为正，说明理想B2-NiAl晶体本征上是延性的金属间化合物，这一点已被Levit等人［34］对［123］软取向NiAl单晶的实验研究所证实，即：当很好地控制NiAl单晶中杂质原子、热空位、组分缺陷、晶体取向、表面处理、预变形时，可得到NiAl单晶高达28%的室温伸长率。Ag合金化时，随着合金化浓度从0增加到1%，图3显示Cauchy压力C12-C44值在0～0.6%以及0.7%～1%区间，相对于合金化前都有所增加，表明在上述两个合金化浓度区间Ag将提高NiAl晶体材料的延性，同样也反映出合金化浓度在0.6%左右最好。

考虑到晶体缺陷对金属间化合物的物理与弹性性质起着非常重要的作用，比如RuAl单晶室温塑性虽然比NiAl单晶差，但其点缺陷结构对塑性降低程度的影响却没有NiAl大，从而导致含有点缺陷结构的RuAl合金实际室温塑性比NiAl好［9］，而B2-YX(X=Cu，Rh，Ag，In)金属间化合物之所以表现出良好的室温延性，除了他们呈本征延性外，多晶材料中存在的点缺陷对其延性的积极影响也是重要原因之一［8］。由此推测：NiAl基合金室温塑性比较差可能源于其对结构缺陷与环境的高敏感性［35］，因此，本工作进一步对Ag合金化时缺陷NiAl晶体的弹性性质进行了计算。

2.3 缺陷NiAl晶体Ag合金化时的弹性性质

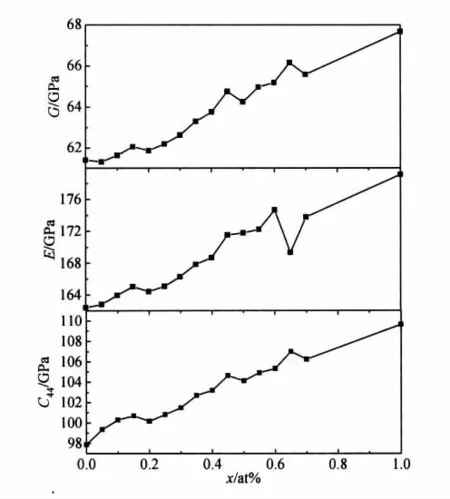
图2 B2-NiAl晶体C44，E，G随Ag合金化浓度x的变化Fig.2 The elastic constant C44，the elastic modulus E and the shear modulus G of B2-NiAl crystals as a function of Ag alloying concentration x

图3 B2-NiAl单晶Cauchy压力C12-C44和多晶G/B0比值随Ag合金化浓度x的变化Fig 3 The Cauchy pressure parameter(C12-C44)and the G/B0of B2-NiAl crystals as a function of Ag alloying concentration x

NiAl金属间化合物中的点缺陷结构主要为Ni空位和Ni反位［36，37］，因此本工作另计算了Ni空位(见图1c)与Ni反位(见图1d)缺陷NiAl单晶低浓度Ag合金化时的弹性常数。相应的单晶 C44和Cauchy压力C12-C44值与多晶弹性模量E、剪切模量G和G/B0比值随Ag合金化浓度x变化的曲线如图4与图5所示。当Ag合金化浓度x=0时，比较图2、图4a与图5a可见，相对于无缺陷的理想NiAl晶体，Ni空位与Ni反位的存在使NiAl晶体的弹性模量E分别提高75.4GPa和54.2GPa、剪切模量 G分别提高35.4 GPa和23.1 GPa;比较图3、图4b与图5b可见，Ni空位与Ni反位的存在分别使NiAl晶体G/B0值增大 0.27和 0.12，Cauchy压力 C12-C44值分别从55.1GPa减小至-15.3GPa和24.5GPa，表明NiAl晶体中点缺陷的存在使其硬度增加的同时也使材料延性大幅降低［9，35］。

进一步分析图4a与图5a可见，与无缺陷理想NiAl晶体情形不同(见图2)，随着Ag合金化浓度的增加，缺陷NiAl晶体的弹性模量E和剪切模量G基本上呈现稳步上升的趋势，在Ag合金化浓度x＜1%区间，不论是相对于未合金化完整晶体还是较之于未合金化的缺陷晶体，都明显可见Ag合金化时(Ni1-xAgx)Al多晶E和G值的提高，并且Ag合金化对缺陷晶体的强化程度比对完整晶体的更显著。可见Ag的固溶强化同样使缺陷NiAl晶体的硬度也大幅提高。

图4 Ni空位B2-NiAl单晶C44和Cauchy压力C12-C44与多晶E，G和G/B0比值随Ag合金化浓度x的变化Fig.4 The elastic constant C44，Cauchy pressure(C12-C44)of B2-(Ni1-xAgx)Al single crystals with Ni vacancy defect and the elastic modulus E，the shear modulus G and the ratio G/B0of corresponding polycrystals as a function of Ag alloying concentration x

而由图4b可见：当Ag合金化浓度x＜0.5%时，单晶Cauchy压力参数C12-C44值震荡不定，但基本上较未合金化时的有所提升，多晶G/B0值也较未合金化时的有所降低，表明在这一合金化浓度范围Ag对含Ni空位的NiAl多晶材料延性有改善作用，并以x=0.32% ～0.48%时，Ni空位的NiAl多晶延性的提升幅度尤为明显。而当Ag合金化浓度1%＞x＞0.5%时，Ag对Ni空位的NiAl晶体的韧化作用则消失。

由图5b可知Ni反位的情况：当Ag合金化浓度x＜0.5%时，虽然对NiAl晶体的韧化没有效果，但在1%＞x＞0.5%高Ag合金化浓度区间，随着Ag合金化浓度的增加，可见Cauchy压力C12-C44的显著升高与G/B0比值明显下降，并在x=0.73%～1%区间呈现相对较好的韧化效果。一个主要的原因很可能源于富Ag相的软化作用［4］。

图5 Ni反位B2-NiAl的晶体C44，E，G以及G/B0比值和Cauchy压力C12-C44值随Ag合金化浓度x变化Fig 5 The elastic constant C44and Cauchy pressure parameter(C12-C44)of B2-(Ni1-xAgx)Al single crystals with Ni anti-site and the elastic modulus E，the shear modulus G as well as the ratio G/B0of corresponding polycrystals as a function of Ag alloying concentration x

3 结论

(1)Ag合金化浓度在0～1%范围内均对NiAl晶体的硬度有明显影响，无论点缺陷存在与否，Ag合金化均可使B2-NiAl晶体的硬度大幅提高。在0～0.6%以及0.7%～1%区间，Ag将提高NiAl完整晶体材料的延性，并且以0.6%左右为最好。

(2)Ni空位或Ni反位降低B2-NiAl晶体的本征延性。当x≤0.5%时，Ag合金化能改善Ni空位的NiAl多晶材料延性，尤其x=0.32% ～0.48%时，Ni空位的NiAl多晶延性的提升幅度尤为明显;当1%＞x＞0.5%时，可明显提高Ni反位B2-NiAl晶体的延展性，在x为0.73% ～1%时呈现相对较好的韧化效果。

志谢：湖南大学材料科学与工程学院彭平教授课题组提供CASTEP软件与技术支持。

［1］DAROLIA R.Structural applications of NiAl［J］.J Mater Sci Technol，1994，10(3)：157-169.

［2］MORINAGA M，SAITO J，YUKAWA N，et al.Electronic effect on the ductility of alloyed TiAl compound［J］.Acta Mater，1990，38(1)：25-29.

［3］刘震云，林栋梁，黄伯云，等.NiAl金属间化合物研究现状［J］.机械工程材料，1998，22(2)：1-5.

［4］周健，郭建亭，李谷松.Ag对NiAl合金组织和性能的影响［J］，材料工程，2002，3：7-10.

［5］DAROLIA R，LAHRMAN D，FIELD R.The effect of iron，gallium and molybdenum on the room temperature tensile ductility of NiAl［J］.Scripta Metall Mater，1992，26 (7)：1007-1012.

［6］MUNROE P R，GEORGE M，BAKER I，et al.Microstructure，mechanical properties and wear of Ni-Al-Fe alloys［J］.Mater Sci Eng A，2002，325(1)：1-8.

［7］陈律，彭平，李贵发，等.L10-TiAl金属间化合物Mn、Nb合金化电子结构的计算［J］.航空材料学报，2005，25(5)：15-19.

［8］陈律，彭平，韩绍昌.B2-YX(X=Cu，Rh，Ag，In)点缺陷结构及其基本物性的理论计算［J］.稀有金属材料与工程.2007，36(12)：2089-2093.

［9］陈律，彭平，李贵发，等.B2-RuAl点缺陷结构的第一原理计算［J］.稀有金属材料与工程.2006，35(7)：1065 -1070.

［10］陈律，彭平，韩亚利.L10-TiAl基本物性的计算与比较研究［J］.材料科学与工艺，2007(1)：47-51.

［11］陈律，彭平，湛建平，等.Ru合金化Ni/Ni3Al相界断裂功的第一原理计算［J］.中国有色金属学报，2008，18 (5)：890-896.

［12］XU D S，LI D，HU Z Q.Substitution Behavior in NiAl-a First Principle Prediction Considering Lattice Relaxation［J］.Mater Res Soc Symp Proc，1999，538：377-382.

［13］郭建亭.有序金属间化合物镍铝合金［M］，北京：科学出版社，2003：66-69.

［14］SEGALL M D，LINDAN PHILIP J D，PROBERT M J，et al.First-principles simulation：ideas，illustrations and the CASTEP code［J］.J Phys：Condens Matter，2002，14 (11)：2717-2744.

［15］VANDERBILT D.Soft self-consistent pseudopotentials in a generalized eigenvalue formalism［J］.Phys Rev B，1990，41(11)：7892-7895.

［16］MARLO M，MILMAN V.Density-functional study of bulk and surface properties of titanium nitride using different exchange-correlation functionals［J］.Phys Rev B，2000，62(4)：2899-2907.

［17］WHITE J A，BIRD D M.Implementation of gradient-corrected exchange-correlation potentials in car-parrinello total-energy calculations［J］.Phys Rev B，1994，50(7)：4954-4957.

［18］FISCHER T H，ALMLOF J.General methods for geometry and wave function optimization［J］.J Phys Chem，1992，96(24)：9768-9774.

［19］FRANCIS G P，PAYNE M C.Finite basis set corrections to total energy pseudopotential calculations［J］.J Phys：Condens Matter，1990，19(2)：4395-4404.

［20］PULAY P.Ab initio calculation of force constants and equilibrium geometries in polyatomic molecules I：Theory［J］.Mol Phys，1969，17(2)：197-204.

［21］SOUVATZIA P，KATSNELSON M I，SIMAK S.Firstprinciples prediction of superplastic transition-metal alloys［J］.Phys Rev B，2004;70：012201-012203.

［22］RAMER N J，RAPPE A M.Virtual-crystal approximation that works：Locating a compositional phase boundary in Pb(Zr1-xTix)O3［J］.Phys Rev B，2000，62：R743-R746.

［23］VILLAS P，CALVERT L.Pearson's Handbook of Crystallographic data for Intermetallic Phases：2nd Edt［M］.OH USA：ASM International(OH)，1991.

［24］张永刚，韩雅芳，陈国良，等.金属间化合物结构材料［M］.北京：国防工业出版社，2001：120.

［25］WASILEWSKI R J.Elastic Constants and Young's Modulus of NiAl［J］.Trans TMS AIME，1966，236：455-457.

［26］FARKAS D，MUTASA B，VAILHE C，et al.Interatomic potentials for B2NiAl and martensitic phases［J］.Modelling Simul Mater Sci Eng，1995，3(2)：201-214.

［27］VOTER A F，CHEN S P.Accurate interatomic potentials for Ni，Al and Ni3Al［J］.Proc Symp Mater Res Soc，1987，82：175-180.

［28］RAO A I，WOODWARD C，PARTHASARATHY T A. Empirical interatomic potentials for L10TiAl and B2NiAl［J］.Proc Symp Mater Res Soc，1991，213：125-130.

［29］JHI S H，IHM J，LOUIE G S，et al.Electronic mechanism of hardness enhancement in transition-metal carbonitride［J］.Nature，1999，6726(399)：132-134.

［30］CHEN K Y，ZHAO L R，JOHN R，et al.Alloying effects on elastic properties of TiN-based nitride［J］.J Phys D：Appl Phys，2003，36：2725-2729.

［31］PUGH S F.Relations between the elastic moduli and the plastic properties of polycrystalline pure metals［J］.Philos Mag，1954，45：823-843.

［32］WANG J Y，ZHOU Y C.Polymorphism of Ti3SiC2ceramic：First-principles investigation［J］.Phys Rev B，2004，69：144108-144121.

［33］PETTIFOR D G.Theoretical predictions of structure and related properties of intermetallics［J］.Mater Sci Technol，1992，8(4)：345-349.

［34］LEVIT V I，BUL I A，HU J，et al.High tensile elongation of β-NiAl single crystals at 293 K［J］.Scripta Mater，1996，34(12)：1925-1930.

［35］DAROLIA R，WALSTON W S，NOEBE R，et al.Mechanical properties of high purity single crystal NiAl［J］. Intermetallics，1999，7(10)：1195-1202.

［36］WÜRSCHUM R，BADURA-GERGEN K，KÜMMERLE E A，et al.Characterization of radiation-induced lattice vacancies in intermetallic compounds by means of positronlifetime studies［J］.Phys Rev B，1996，54(2)：849-856.

［37］PIKE L M，CHANG Y A，LIU C T.Point defect concentrations and hardening in binary B2intermetallics［J］.Acta Mater，1997，45(9)：3709-3719.