正交面齿轮传动系统分岔特性

杨 振，王三民，范叶森，刘海霞

(西北工业大学机电学院，710072西安，yang95478@163.com)

进入21世纪以来，国外学者［1-4］对面齿轮的啮合原理、齿轮弯曲强度、齿面接触强度、切齿及磨齿加工、面齿轮疲劳寿命实验等进行了研究.国内学者［5-7］近几年对面齿轮的研究目前主要集中于齿面设计、齿轮弯曲强度、齿面接触强度、切齿加工等方面，关于其振动特性的研究还处于初期阶段.由于面齿轮传动系统含有间隙、时变啮合刚度、齿轮误差等参数，其本质上是一个强非线性系统，其振动特性会直接影响到传动系统的稳定性和可靠性［8］.

本文建立了包含齿侧间隙、时变啮合刚度、综合误差、支承等参数在内的正交面齿轮传动系统的弯-扭耦合非线性动力学模型，并用PNF方法求解了系统的动力学方程组，经分析后得到了系统分岔特性的变化规律.

1 系统的非线性动力学模型与方程

图1所示为根据集中参数理论建立的弹性支承下正交面齿轮传动的系统动力学模型，模型中不考虑绕各坐标轴的摆振.

该模型以直齿轮轴线为x轴，以面齿轮轴线为y轴，并以两轴的交点作为原点建立全局坐标系Σ:(O x y z).由于小齿轮为直齿圆柱齿轮，齿轮上无轴向作用力，因此只考虑2个坐标方向的支承刚度和阻尼，分别为kij、cij(i=y，z;j=p，g).

设主动轮p有驱动力矩Tp，从动轮g有不变的阻抗力矩Tg.整个传动系统共有6个自由度，分别为{Yp，Zp，θp，Yg，Zg，θg}T.

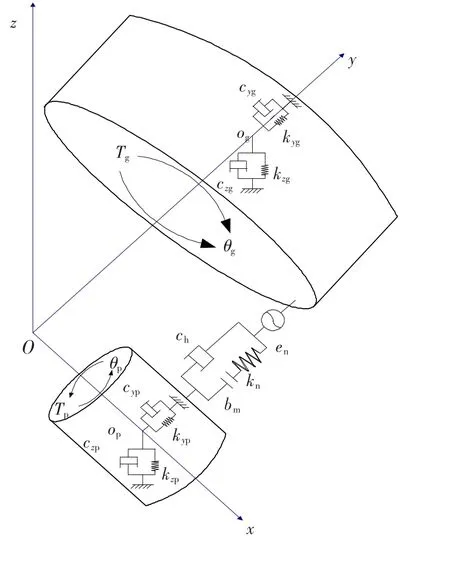
图1 正交面齿轮传动系统非线性动力学模型

2 系统的振动微分方程

由图1可以得到，两齿轮啮合点间因振动和误差产生的沿啮合点法线方向的相对位移λn为

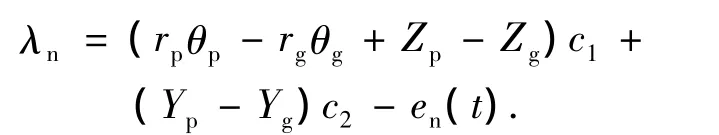
式中:c1=cos αn，c2=sin αn;rp，rg为两齿轮啮合点半径;αn为法面压力角;en(t)为齿轮副的法向综合传动误差.

则齿轮副在啮合时的法向动载荷及其沿坐标轴的分力分别为

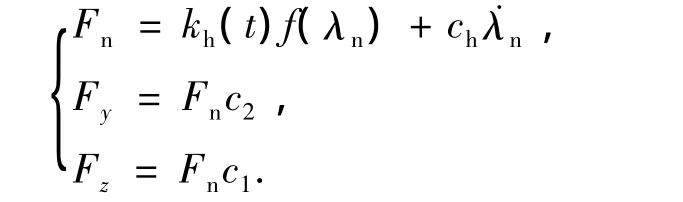
式中:kh(t)为时变啮合刚度;ch为啮合阻尼; f(λn)为间隙函数，其中:

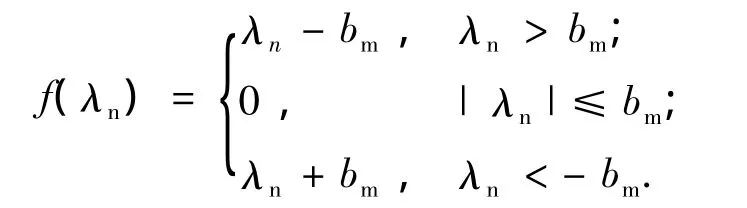
式中，bm为法向平均啮合间隙之半.

下面确定时变啮合刚度kh(t)和齿轮副综合误差en(t)的表达式.

由于面齿轮的空载重合度一般在1.6～1.8，因此实际的面齿轮副的综合啮合刚度是一个以啮合周期为周期的阶跃函数.另外，面齿轮的重合度在加载后会进一步增大，其啮合刚度的变化比较小，因此可以将其处理为在一个平均值下的微小波动，具体表达式如下:

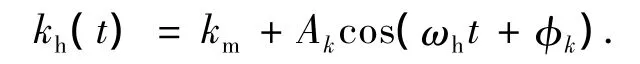
式中，km为啮合刚度的平均值，Ak为啮合刚度的波动幅值，ωh为齿轮副的啮合频率，φk为初相位.

由于对齿轮振动影响较大的误差比较多，如基节偏差、齿距偏差、齿形误差、齿距累积误差等，在此将其统称为齿轮副综合误差.具体的处理方法参考文献［9］，将其表示为啮合频率的简谐函数:

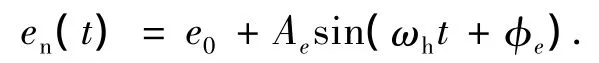
式中，e0为综合误差常值，Ae为综合误差的幅值，φe为初相位.

则图1所示的面齿轮传动系统的振动方程为

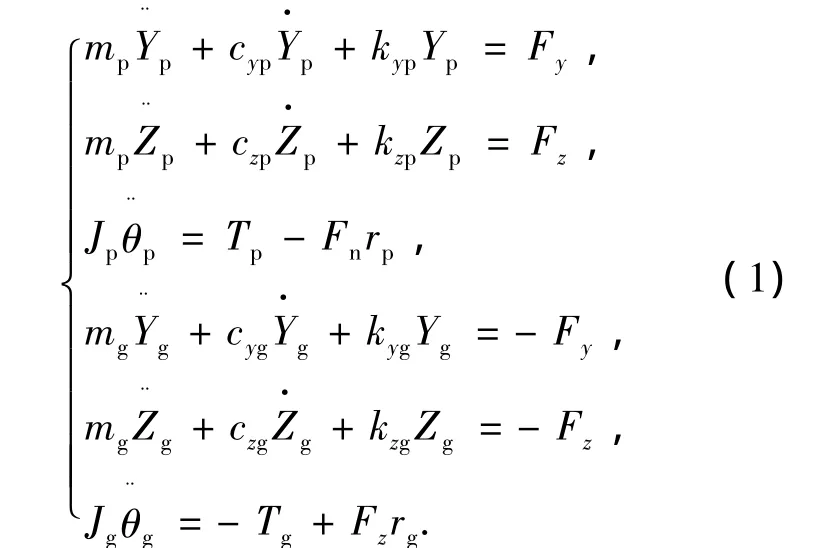
为了消除系统的刚体位移，引入齿面啮合点间的法向相对位移λn作为新的自由度，并对方程组(1)进行量纲一化处理后，得

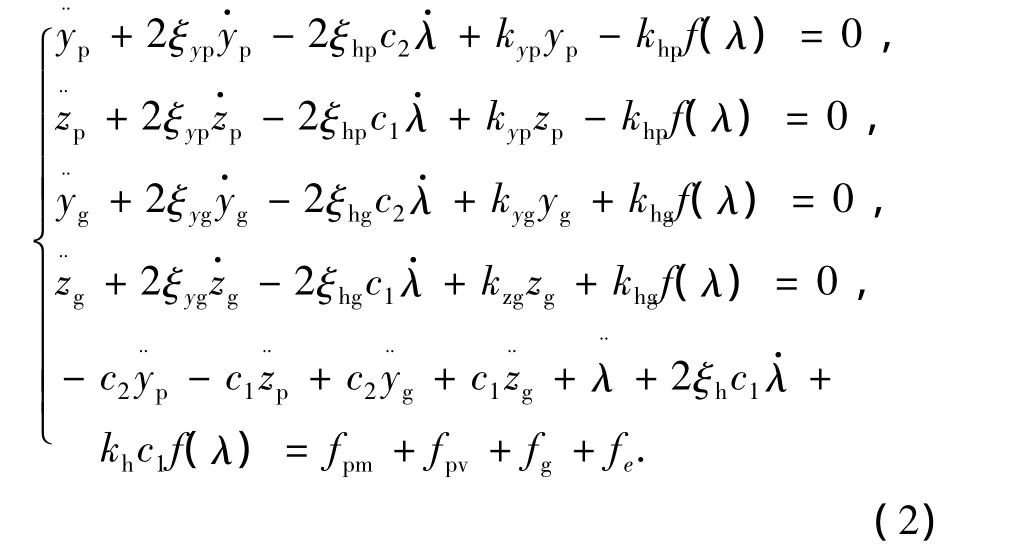
式中:yj=Yj/bm，zj=Zj/bm;λ=λn/bm;

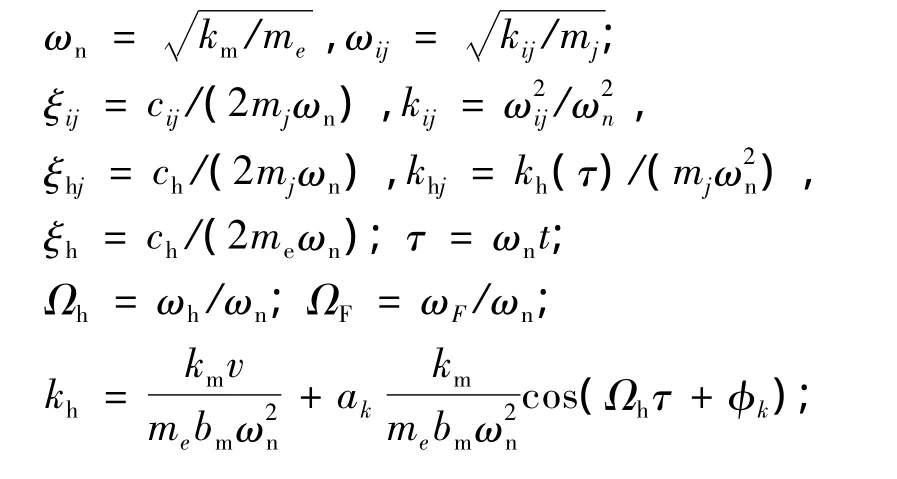
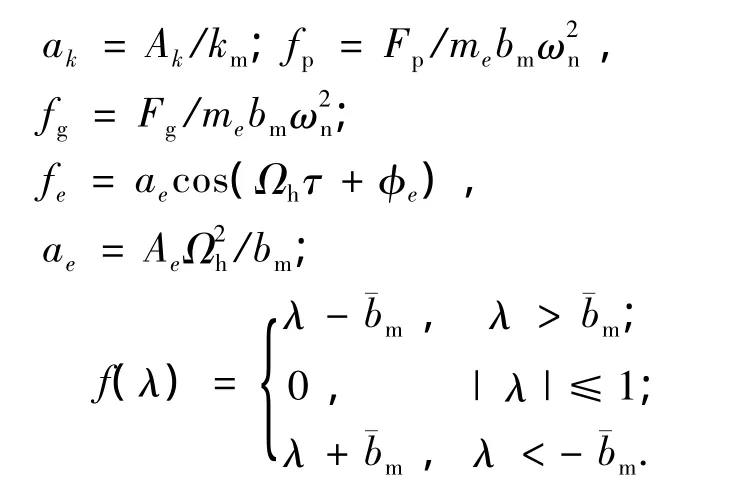
其中，i=y，z;j=p，g.

3 系统的分岔特性分析

对间隙型非线性方程组(2)，用PNF方法(参考文献［10］)对其进行求解，得到的系统响应也以量纲一化的形式给出.

系统主要参数为:齿数zp=36，zg=123;模数m=4 mm;齿宽B=30 mm;压力角αn=20°;传动误差均值e0=0 μm，幅值Ae=15 μm，初始相位角φe=0;驱动转矩Tp=300 N·m;负载转矩Tg=1 025 N·m;齿侧间隙bm=100 μm;啮合刚度km=3.2×108N·m-1;小直齿轮支承刚度kyp=kzp=2.8×108N·m-1，面齿轮支承刚度kyg=kzg=5.2×108N·m-1.

3.1 系统的倍周期分岔

图2为时变啮合刚度幅值系数ak从0.4增大到0.5的过程中系统的倍周期分岔特性图.由系统的庞加莱截面图可见，在ak=0.420处系统响应依然为5周期次谐响应(图3(a));当增大到0.460时，系统分岔为 10周期次谐响应(图3(b));然后在ak=0.485处进一步分岔为26周期次谐响应(图3(c));其后的分岔域越来越短，最后进入混沌响应(如图3(d)).

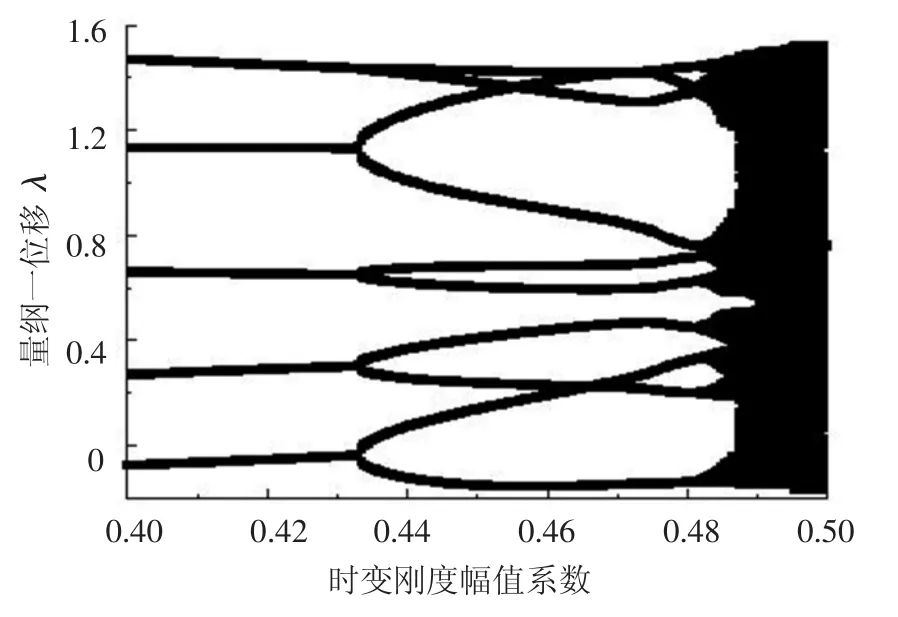
图2 系统倍周期分岔图(ak=0.4～0.5)

3.2 系统的拟周期分岔

当啮合阻尼比ξg由0.061减小到0.060时，可以观察到系统响应由拟周期道路到达混沌的过程，如图4所示.

图3 不同时变啮合刚度幅值系数ak对应的系统庞加莱截面图

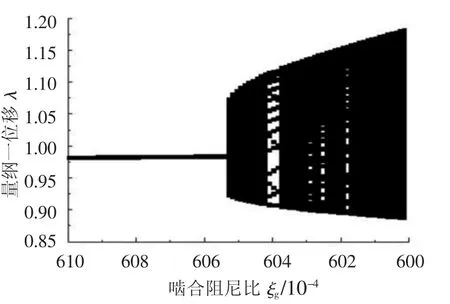
图4 系统拟周期分岔图(ξg=0.061～0.060)

由各参数点处系统响应的庞加莱截面图可见，在ξg=0.060 510 0附近系统响应为拟周期响应，如图5(a)所示;当ξg减小到0.060 416 9时，系统的拟周期环面破碎为数个小的吸引子区域，如图5(b)所示;当ξg继续减小到0.060 390 0时，系统响应为17周期次谐响应，如图5(c)所示;随着ξg进一步减小到0.060 375 0附近时，系统再次进入拟周期响应，如图5(d)所示.经过一系列的拟周期分岔后，系统最终进入混沌响应，此时系统响应相图和庞加莱截面图如图5(e)、图5 (f)所示.

由以上分析可以看出，啮合阻尼比从0.061减小到0.060的过程中，系统响应经历了周期—拟周期—拟周期环破碎—周期—拟周期…的拟周期分岔道路.

3.3 系统的边界激变

在一定的参数条件下，还可以观察到系统通过边界激变到达混沌响应的现象.

图6所示即为改变综合传动误差幅值ae时系统的激变，当ae=0.116时，系统响应为2周期响应(图7(a));当ae传减小到0.115附近时，系统响应发生激变进入混沌响应，如图7(b)所示.

图5 不同啮合阻尼比ξg对应的系统庞加莱截面图

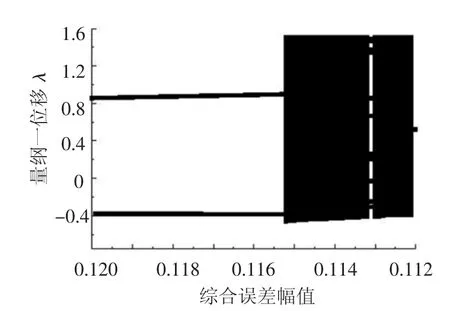
图6 系统激变分岔图(ae=0.120～0.112)

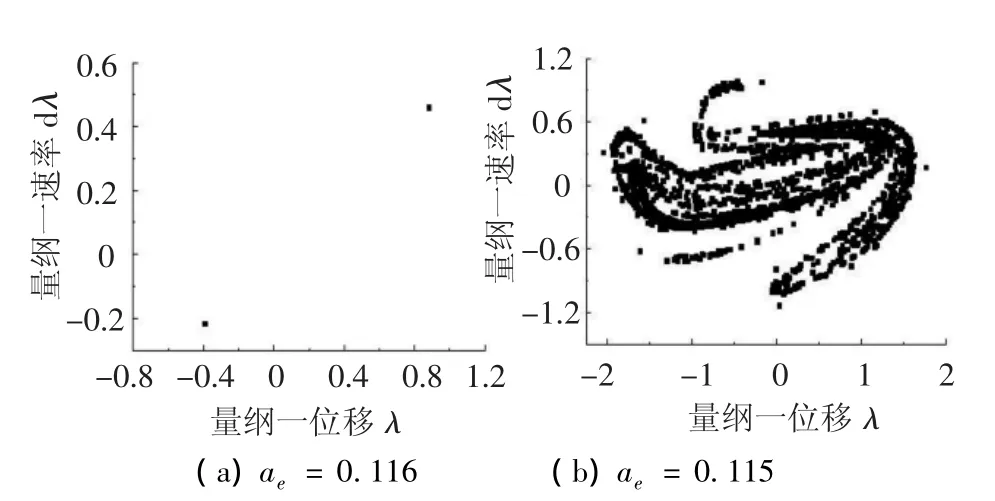
图7 不同综合误差幅值ae对应的系统庞加莱截面图

4 结论

1)建立了包含支承、齿侧间隙、时变啮合刚度、综合传动误差、阻尼和外激励等参数的面齿轮传动系统的非线性动力学模型.

2)系统通向混沌的途径主要有周期倍化道路、拟周期道路以及边界激变.

3)不同的系统参数，甚至同一参数的不同区段，系统会以不同的道路进入混沌区域.

［1］LITIVIN F L，ALFONSO F，LAUDIO Z Z，et al.Design，generation and TCA of new type of asymmetric face-gear drive with modified geometry［J］.Computer Methods in Applied Mechanics and Engineering，2001，190(3):5837-5865.

［2］LITIVIN F L，ALFONSO F，CLAUDIO Z Z，et al.Design，generation，and stress analysis of two versions of geometry of face-gear drives［J］.Mechanism and Machine Theory，2002，37(4):1179-1211.

［3］LITIVIN F L，IGNACIO G P，ALFONSO F，et al.Design，generation and stress analysis of face-gear drive with helical pinion［J］.Computer Methods in Applied Mechanics and Engineering，2005，194(9):3870-3901.

［4］GUINGAND M L，de VAUJANY J P，LCARD Y.Analysis and optimization of the loaded meshing of face gears［J］.Journal of Mechanical Design，2005，127(1): 135-143.

［5］李政民卿，朱如鹏.面齿轮插齿加工中过程包络面和理论齿廓的干涉［J］.重庆大学学报:自然科学版，2007，30(5):55-58.

［6］贺鹏，刘光磊.面齿轮传动安装误差特性研究［J］.机械科学与技术，2008，27(1):92-95.

［7］郭辉，赵宁，方宗德，等.基于接触有限元的面齿轮传动弯曲强度研究［J］.航空动力学报，2008，23(8): 1438-1442.

［8］LEWICKI D G，HEATH G F.RDS-21 face-gear surface durability tests［C］//AHS International 63rd Annual Forum Proceedings.Virginia Beach:American Helicopter Society，2007:1018-1027.

［9］唐增宝，钟毅芳.齿轮传动的振动分析与动态优化设计［M］.武汉:华中理工大学出版社，1994:36-37.

［10］杨振，王三民，范叶森，等.转矩分流式齿轮传动系统的非线性动力学特性［J］.机械工程学报，2008，44(7):52-57.