一种快速KMSE算法及其在异常入侵检测中的应用

范自柱，徐 勇，徐保根，朱 旗

(1.哈尔滨工业大学深圳研究生院，518055广州深圳，zzfan3@yahoo.com.cn; 2.华东交通大学基础科学学院，330013江西南昌)

核方法［1］的基本思想是将输入空间通过某种非线性映射变换到一个高维的特征空间，借助于“核技巧”［2］在新的空间中应用线性分析方法.“核技巧”最早应用于支持向量机(Support Vector Machines，SVM)中.随后，基于核的主分量分析(Kernel Principal Component Analysis，KPCA)［3］、基于核的Fisher鉴别分析(Kernel Fisher Discriminant Analysis，KFDA)［4］和基于核的最小均方误差(KMSE)［5］等核学习方法被提出.实际上，KMSE模型可以看作是在核主分量分析基础上实施特征提取的过程，而且在形式上它等效于最小平方支持向量机(Least Squares Support Vector Machines，LS-SVM)［6］与核鉴别分析.当样本数趋于无穷时，KMSE模型将以最小均方误差逼近特征空间中的贝叶斯判别函数.

根据再生核理论，KMSE模型在特征空间中的鉴别向量是此空间中样本的线性组合.相应地，KMSE模型对一个样本的特征抽取结果为该样本与所有(训练)样本间核函数的线性组合.因此，KMSE特征抽取效率与训练集的大小成反比.为了提高学习效果，人们往往需要数百甚至成千上万个样本进行学习(训练)，而这样大规模的训练集无疑会大大降低KMSE的特征抽取效率.针对这一问题，一些关于核的优化算法［7-10］被相继提出.本文首次将KMSE和其快速算法应用于异常入侵检测［11］这一信息安全领域，在经典的入侵检测实验数据集KDDCUP1999上的实验结果表明，KMSE是一种有效的异常入侵检测方法，经改进后得到的快速KMSE方法检测效率非常高，检测结果十分理想.

1 KMSE模型

KMSE是对传统的最小均方误差(MSE)应用核方法而得到的.本文主要考虑2类问题:假设在n个训练样本 x1，x2，…，xn中，前 n1个属于第1类，类别标识为1;其余的n2个属于第2类，类别标识为-1，且n1+n2=n.这些样本经过一非线性映射φ(·)得到特征空间中的2组样本: φ(x1)，φ(x2)，…，φ(xn1)对应第1类;φ(xn+1)，…，φ(xn)对应第2类.则KMSE模型为

其中:

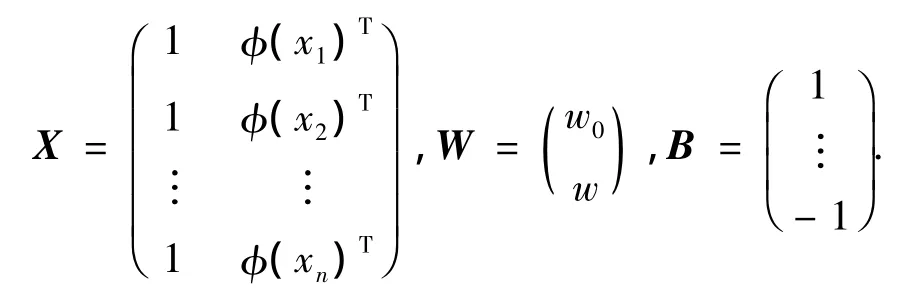
式中:W为特征空间中的鉴别方向;w为鉴别矢量;w0为阈值权;B中1的个数为n1，-1的个数为n2.根据再生核理论，W可以看作为阈值权w0与特征样本的线性组合［13］，式(1)中的W变为

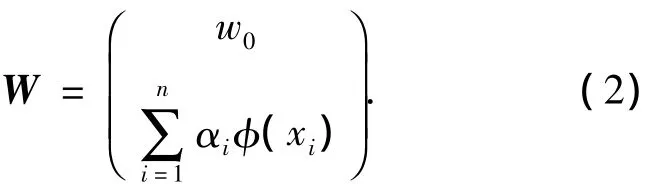
因此，借助核函数k(x，xi)=(φ(x)· φ(xi))，式(1)可以改写为

其中:

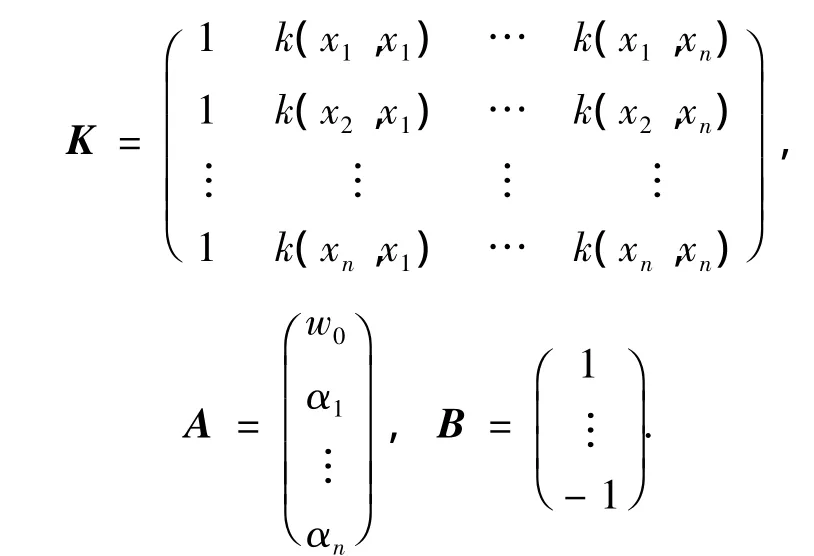
式(3)的最小二乘解的一般形式为

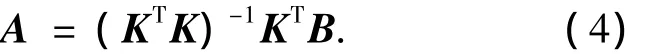
由于KTK是病态矩阵，所以需要引入一正则项μ，则式(4)变为

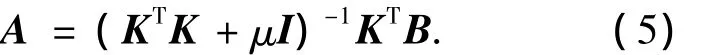
式中:I为单位矩阵;A即为将min(μATA+(BKA)T(B-KA))作为目标函数得出的解.根据式(5)求出A后，便可实现分类.设有一待测模式x，它在鉴别方向上的投影为

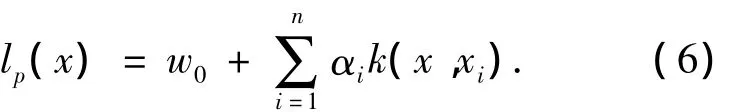
当lp(x)＞0时，将x分到第1类，其类标记为1;否则，它被分到第2类，其类标记为-1.

2 KMSE的快速算法(FKMSE)

由式(2)知，如果要确定一个样本的类别，需要把它与所有训练样本的点积求出，才能判别其类别.当训练样本非常多时，若要给大容量的测试集分类，显然，其效率是不高的.在输入空间中，训练样本的维数一般不是很高.由线性相关性理论，n+1个n维向量必线性相关，所以，当训练样本的个数大于其维数时，训练样本间必然存在线性相关性.根据线性相关理论，得出下面的结论:

定理1 对于特征空间F中的一组向量: φ(x1)，φ(x2)，…，φ(xr)∈F，如果它们线性相关，即存在一组不全为0的数:l1，l2，…，lr∈R，使得:

则有

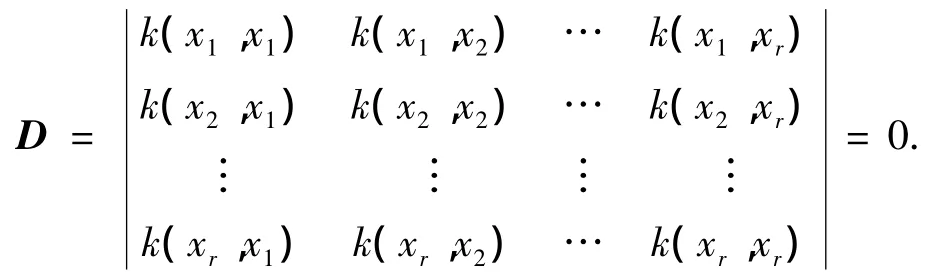
证明 依次用φ(x1)，φ(x2)，…，φ(xr)乘式(7)左右两边，得:

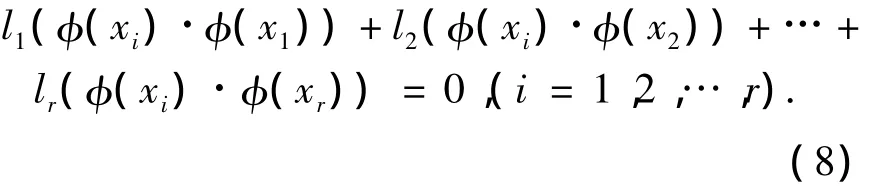
定义核函数k(x，xi)=(φ(x)·φ(xi))，得出齐次线性方程组为

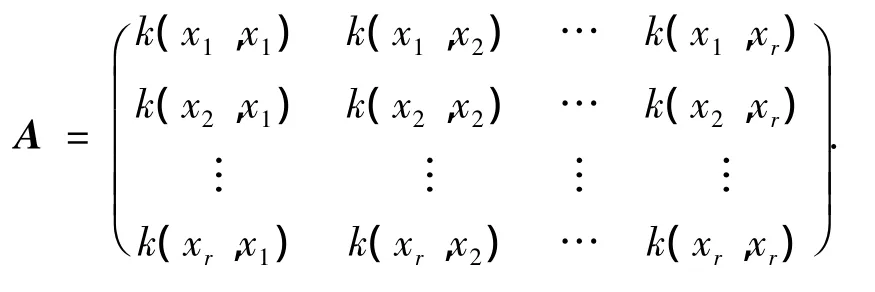
其中，L=(l1，l2，…，lr)T，显然，A是方阵，根据求解线性方程组的Crame法则，齐次线性方程组若有非零解，则det(A)=0，即D=0.由题设，l1，l2，…，lr不全为零，也即是式(9)有非零解，所以有D=0.得证.

定理1的逆否命题也很有用，即:若D≠0，则φ(x1)，φ(x2)，…，φ(xr)线性无关.

利用定理1，可以判断特征空间中的一组向量是否线性相关，如果相关，则根据某个准则选取该向量组的一个极大无关组，用这个无关组代替原向量组，从而可以减少鉴别方向W中涉及向量的个数.这样，式(6)中的n将减小，测试时所需的计算代价变小，因此，能够提高分类效率.理论上，一个向量组与它的极大无关组等价，也就是能够相互线性表示，而且，一个向量组往往不止一个极大无关组.在实际应用中，极大无关组的形式越简单往往被使用得越多，如单位向量组.在本文应用中，主要考虑方程组的求解误差，也就是训练模式向量对应的准则值.根据式(5)，本文选取的准则为:J即给出快速算法过程:

1)计算每个训练模式x1，x2，…，xn对应的准则值J.为了计算J，必须先计算每个xi(i=1，2，…，n)对应的矩阵K'为

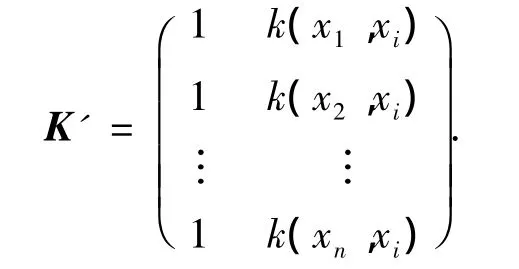
计算出K'后，把K'代入式(5)中求出A，最后把每个J计算出来，并且依J值的大小用快速排序法将xi(i=1，2，…，n)按升序排成一序列，记为R;令极大无关组B={}.

2)从R中选出第1个元素x1'，计算它对应的D=|k(x1'，x1')|，把x1'加入B，使其成为B的第1个元素:B={x1'}，R=R-{x1'}.

3)B中其他元素的确定.correlate(B)表示与B中所有元素线性相关的样本.设经过第i-1步选择，B中有i-1个元素，B={x1'，x2'，…，xi'-1}，与其对应的行列式为

取R中元素xi'，令

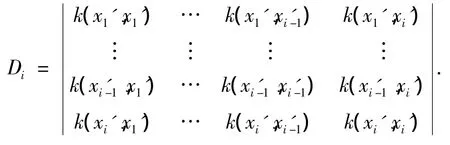
若Di=0，xi'∈correlate(B).则确定B中其他元素的过程的伪语言描述为:

最后获得基样本集B={x1'，x2'，…，xs'}.

4)用基样本集B代替整个训练样本集，修改式(6)，得:

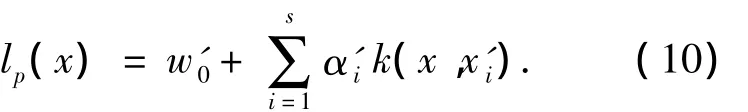
利用式(10)，可以对一待测模式x进行分类.一般地，s≪n，所以对待测样本的分类速度将会大大提高.

3 实验

本文实验包括2个部分:实验1和实验2.它们都是在2.4 GHz CPU，256 M内存环境中使用Matlab7.0实现.

3.1 实验1

在实验1中，使用文献［5，9］中提到的基准数据库，在7个基准模式集上进行.每个模式集被随机分成了100个部分，每个部分又包括4个子部分:训练数据集、训练标记集、测试数据集和测试标记集.实验采用高斯型核函数为

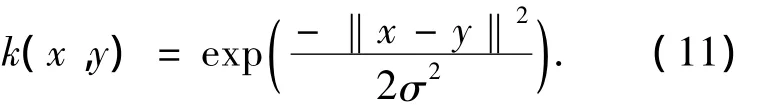
实验时，先对每个数据集的第1个子集进行训练，然后对100个测试集测试.按照这种方式，先在基准数据集上，根据式(5)实现了传统的KMSE方法(TKMSE).一方面是为了与新提出的方法FKMSE在算法效果方面进行对比;另一方面，是为了确定核函数中的参数，实验结果如表1所示.表1最后1列括号中的值为最优的核函数参数，式(5)中的正则项μ取1.0E-3.

表1给出了TKMSE、NKNM、FKNM、AB、SVM和FKMSE等6种方法的平均分类错误率及其标准差.其中:AB和SVM这2种方法的结果引自文献［5］;NKNM和FKNM这2种方法的结果引自文献［9］.表1中的分类效果由2项构成:第1项是100次测试所得的平均分类错误率;第2项是其标准差.对于每一数据集，表1中的括号项标出了使用5种方法NKNM、FKNM、AB、SVM和本文提出的FKMSE得到的最好分类效果.由表1看出，FKMSE与除TKMSE外的其他4种方法分类效果相当;对于数据集f.solar，FKMSE是5种非TKMSE方法中分类最好的.

表2给出了FKMSE和FKNM方法中的基样本数及其与总训练样本数的比例，基样本数后面的百分比是指一次训练得到的基样本个数与训练样本数之比.此比例普遍较低，7个数据集中最高的是15%，有的甚至低至约1%.这就是本文方法实现速度快的根本原因.同时，从分类效果来看，FKMSE与原方法TKMSE相差无几，基本可以取代原训练样本进行分类.从表1和表2中可以看出，虽然FKMSE的分类效果比TKMSE稍微下降一点，总体分类正确率下降大约2%.但是，它的效率大大提高了.表3给出了FKMSE和TKMSE这2种方法的分类时间.这里的分类时间是指测试100次所需要的时间，表中括号中的数值是FKMSE与TKMSE分类时间的比例.从表3可以看出，文中提出的快速算法比传统的方法测试速度要快一个数量级以上，极大地提高了分类效率.而且，根据表2和3，数据集的训练样本越多，本文方法的分类效率就越高.

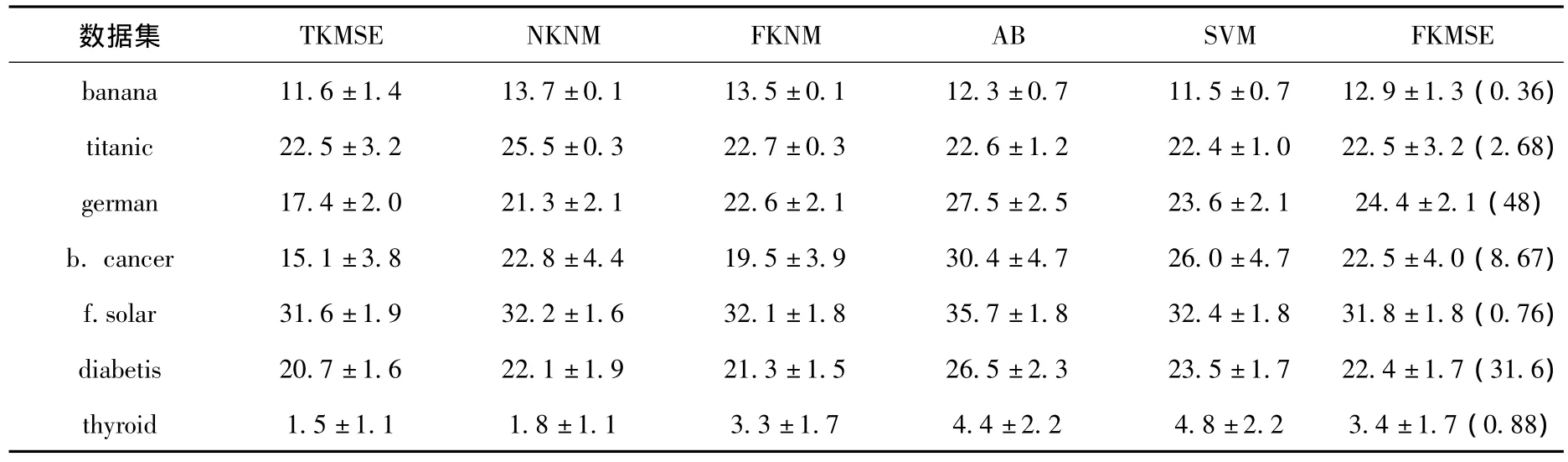
表1 分类错误率和标准差

表2 FKMSE和FKNM方法中的基样本数及其与总训练样本数的比例

表3 FKMSE和TKMSE分类时间

3.2 实验2

本文选用在入侵检测领域中的经典测试数据集KDDCUP1999［12］.该数据集主要由6个部分组成，实验在其中的一个子集kddcup.data-10-percent.gz上进行.这个子集包含约49万个样本，每个样本有41个特征.本文把数据集中的数据分成2类:1)正常数据，即类别表示为“normal”的数据; 2)异常数据，包含4类攻击:DOS、PROBE、R21和U2R.本文实验的训练集选取2 000个样本，由2类组成:1)“normal”;2)DOS攻击类型之一的“smurf”类，每类1 000个样本，都是随机抽取.测试集在kddcup.data-10-percent.gz中按先后顺序选取10 000个样本，分为10个测试子集，每个1 000个样本，样本的类别与训练集一致.

实验中，通过预处理，去除了12个特征，采用29个特征进行计算.实验也选用形如式(11)的高斯核函数，其参数选为训练样本方差的均值.其他参数同实验1.

表4给出了2种方法KMSE和FKMSE的入侵检测效果和时间.实验中的检测效果用平均检测率表示，一次检测率是指在一次测试中正确检测出的攻击次数与总的攻击次数之比.平均检测率则是对10个测试子集进行检测所得到的检测率均值.表中检测时间是指对10个测试子集进行检测所需的时间.从表4中可以看出，2种方法的检测效果皆很理想，所以它们都是异常入侵检测的有效方法.值得注意的是，本文提出的FKMSE方法在实验中，不仅检测效果很好，而且非常高效，其检测时间只有KMSE方法的0.2%.因此，比KMSE方法更适合实时大规模异常入侵检测.根据表4，在硬件条件不高的情况下，用FKMSE方法对10 000个样本检测，只需要2.9 s，就可以完全达到实时入侵检测的要求.

表4 KMSE和FKMSE的检测效果和时间

4 结论

1)原始输入空间的样本经非线性映射后变成特征空间的样本，它们之间往往存在线性相关性.因此，如果通过训练学习，剔除线性相关性，减少参与计算的样本的个数，将会提高分类效率.

2)FKMSE适合实时大规模异常入侵检测.

［1］TAYLOR S，CRISTIANINI N.Kernel methods for pattern analysis［M］.London:Cambridge University Press，2004.

［2］ZHANG D，SONG F X，XU Y，et al.Advanced pattern recognition technologies with applications to biometrics［M］.New York:IGI Global，2009.

［3］XU Y，LIN C，ZHAO W.Producing computationally efficient KPCA-based feature extraction for classification problems［J］.Electronics Letters，2010，46(6):452-453.

［4］MIKA S，RATSCH G，WESTON J，et al.Fisher discriminant analysis with kernels［C］//Neural Networks for Signal Processing IX，1999.Proceedings of the 1999 IEEE Signal Proceesing Society Workshop.Madison，WI:IEEE Press，1999:41-48.

［5］LIU W F，PUSKAL P，JOSE P.The kernel least-meansquare algorithm［J］.IEEE Transactions on Signal Processing，2008，56(2):543-554.

［6］XU Y.A new kernel MSE algorithm for constructing efficient classification procedure［J］.International Journal of Innovative Computing，Information and Control，2009，5(8):2439-2447.

［7］CAWLEY G C，TALBOT C.Efficient leave-one-out cross-validation of kernel fisher discriminant classifiers［J］.Pattern Recognition，2003，36(11):2585-2592.

［8］ZHENG W M，ZOU C R，ZHAO L.An improved algorithm for kernel principal component analysis［J］.Neural Processing Letters，2005，22(1):49-56.

［9］XU Y，ZHANG D，JIN Z，et al.A fast kernel-based nonlinear discriminant analysis for multi-class problems［J］.Pattern Recognition，2006，39(6):1026-1033.

［10］LEE D，JUNG K H，LEE J.Constructing sparse kernel machines using attractors［J］.IEEE Trans on Neural Networks，2009，20(4):721-729.

［11］肖立中，邵志清，马汉华，等.网络入侵检测中的自动决定聚类数算法［J］.软件学报，2008，19(8): 2140-2148.

［12］KDDCUP1999.http://archive.ics.uci.edu/ml/databases/kddcup99/kddcup99.html.