EGO算法的翼型气动外形优化设计

侯成义

(西北工业大学国防科技研究院，710072西安，peggy.cao@163.com)

遗传算法、粒子群算法等随机优化算法同基于梯度的优化算法相比具有很强的全局性和鲁棒性，然而这些随机优化算法进行需要用CFD、FEM分析等耗时的目标值评估的工程优化时，存在着计算量大的问题，严重制约了在工程中的应用.用代理模型代替费时的精确模型计算进行优化的方法得到了发展［1-2］，常用的代理模型有多项式响应面模型、人工神经网络模型、Kriging模型等.首先由一定数量的样本构造代理模型，用优化算法搜索代理模型的最优解并进行精确模型校验，进而更新校验点到代理模型直至满足收敛要求.由于代理模型的计算量比精确模型小得多，该方法可大幅度提高优化效率，但是其优化精度严重依赖于代理模型预测的能力，容易陷入局部最优［3］.M.Schonlau［4］提出的EGO(Efficient Global Optimization)算法在选取校验点时综合考虑了代理模型的预测值和预测精度，有效避免了陷入局部最优的风险，该方法在工程优化中得到了应用［5-6］.

本文采用拉丁超立方实验设计方法产生样本点，用EI(Expected Improvement)最优策略综合评价由Kriging代理模型获取的预测适应值及预测精度，并结合响应最优策略，用粒子群算法搜索最优校验点，结合Hicks-Henne型函数翼型参数化方法与雷诺平均N-S方程流场求解器进行了翼型优化设计.

1 优化系统

1.1 试验设计方法

选取合理分布的样本点对构造代理模型具有重要的影响，一般要求有限的样本应该尽可能全面的反映设计空间的特性.常用的实验设计方法有全析因设计、正交设计、均匀设计等，本文采用了拉丁超立方设计方法产生样本点.

1.2 粒子群优化算法

粒子群优化算法(Particle Swarm Optimization)［7］是一种模拟鸟群觅食行为的群体智能算法，该算法实现简单，参数设置方便，收敛速度快，能有效解决复杂优化问题.该算法以“粒子”作为个体，按照设定的规则进行群体的协作从而进行有效的搜索.首先随机初始化粒子种群位置和初速度，每个粒子通过跟踪自身所找的个体最优粒子pbest以及整个种群找到的全局最优粒子gbest，在粒子当前速度、pbest和gbest的位置的共同引导下，粒子在下一个时刻将飞行到新的位置.粒子的速度和位置更新公式分别为

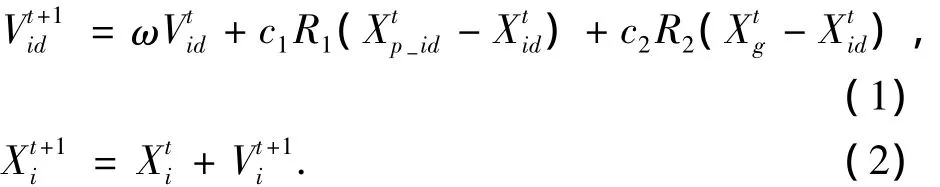
式中:d=1，2，…，n(n为搜索空间维数);i=1，2，…，m(m为种群规模);t为当前进化代数;分别为对应粒子的历史最优位置和全局最优位置;c1，c2分别为学习因子;R1，R2分别为(0，1)的随机数;ω为惯性权重因子，惯性权重因子决定了粒子先前速度对当前速度的影响程度.Shi Y采用随迭代进行惯性权重因子减小的方法，在优化初期提高全局搜索能力，而在后期加速收敛.

1.3 Kriging代理模型

Kriging代理模型［8］起源于地理空间统计学，是一种估计方差最小的无偏估计模型，通过相关函数的作用，具有局部估计的特点，它可以较好的预估未知点处函数值的分布情况.Kriging模型假设目标函数值与设计变量之间的真实关系可以写为

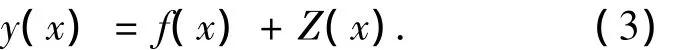
式中:f(x)为回归模型，是对设计空间的全局近似，为确定性部分，可以一个常数β表示;Z(x)为均值为0，方差为σ2的统计过程，表示对全局近似的背离，2个插值点的协方差为

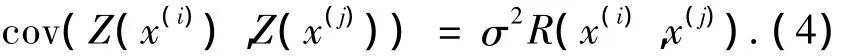
式中R为点x(i)和x(j)的相关函数，可用高斯函数表示为

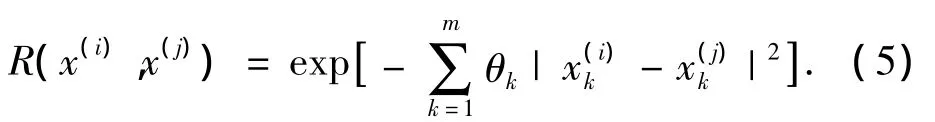
未知点x0处的预测值^y(x0)和方差估计值^σ通过下列形式给出:

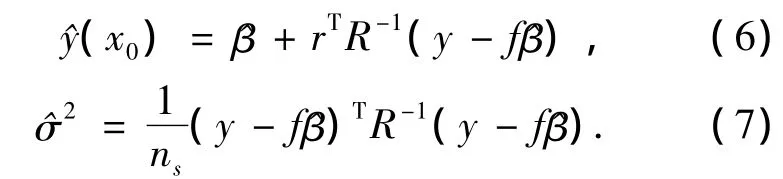
可以通过极大似然估计确定相关参数θk为

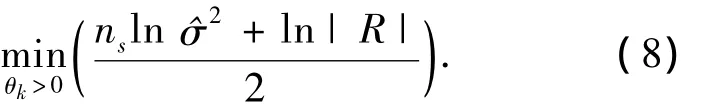
1.4 EGO算法

选择代理模型预测值的最优点作为校验点的方法称为响应最优策略.但是代理模型的预测精度总是有限的，如果代理模型在真实的最优解处预测精度较差，就有可能在选择校验点时总是无法搜索到该区域，使得优化陷入局部最优.因此在选择校验点时有必要综合考虑Kriging模型获取的预测适应值及预测精度.本文采用了EI(Expected Improvement)方法，根据下式确定个体的EI值，EI值越大说明该个体越需要校正.

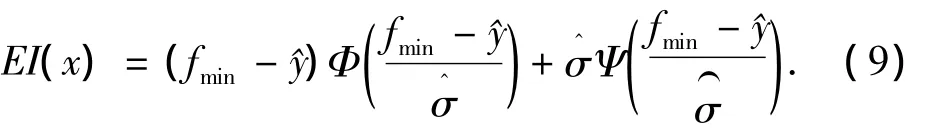
式中:fmin为样本点中最小适应值;^y为预测适应值为预测标准差;Φ，Ψ分别为标准正态分布和标准正态分布密度函数.当个体预测值越小，预测标准差越大，则个体的EI值越大，个体越需要校正.

1.5 优化流程

本文在选择校验点时，一部分校验点用响应最优策略选择，另一部分采用EI最优策略，2种方法交替进行.优化流程为:

1)由拉丁超立方设计方法在设计空间内生成一定数量的样本.

2)由样本点构建Kriging代理模型.

3)确定是采用响应最优策略还是EI最优策略，基于粒子群算法优化选择最优响应或最优EI校验点.

4)判断是否满足收敛条件，如果满足则退出，不满足则执行步骤5).

5)将校验点加入样本，执行步骤2).

2 翼型气动优化设计

翼型参数化方法采用的是Hicks-Henne型函数法［9］，新翼型由基本翼型的上表面或下表面加扰动构成，表达为

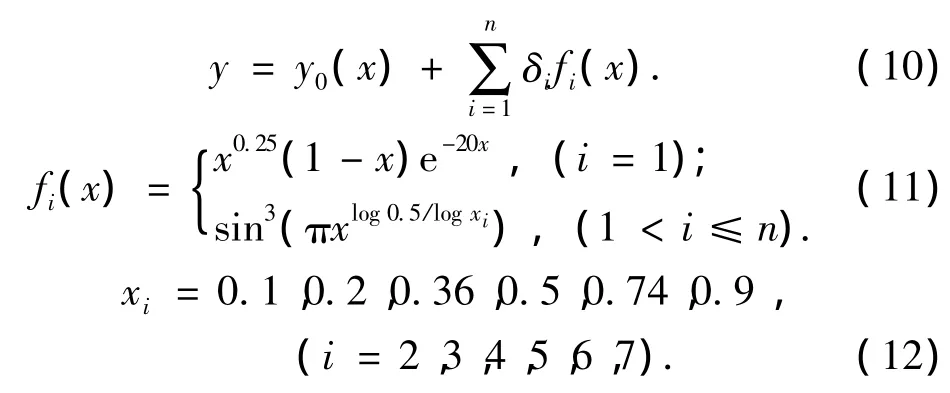
式中n为控制上表面或下表面变量的个数，本文选取n为7，即共计14个设计变量.

本文以RAE2822翼型为初始翼型进行翼型气动优化设计研究.采用雷诺平均N-S方程求解绕翼型流场，湍流模型为k-ω SST模型.设计状态为巡航马赫数0.73，雷诺数6.5E6，设计升力系数0.74，约束条件为最大相对厚度不减，低头力矩特性不差于初始翼型，优化目标为降低阻力系数.

由拉丁超立方设计方法产生120个翼型作为代理模型初始样本点，校验次数为240，EI最优策略进行2次后响应最优策略进行1次，如此交替进行，即分别进行160次和80次，PSO的种群规模为30，迭代步数为60.为了比较本文优化方法，还采用响应最优法和粒子群算法进行翼型优化，其中响应最优法初始样本数为120，校验次数为240，而粒子群算法种群规模为30，迭代步数为40，设计结果如表1所示.单纯的响应最优法优化陷入局部最优，其他2种方法得到了相似的优化结果，阻力降低了22.4%，粒子群算法用了1 200次流场计算，而本文方法仅用360次.图1和图2分别为本文方法优化前后翼型形状和压力分布，与初始翼型相比，设计翼型翼型完全消除了激波，阻力系数降低了0.003 4，而翼型最大相对厚度没有降低.设计翼型整体弯度降低，而通过增加后加载来保持升力系数.同时设计翼型增加了前加载和头部上表面吸力峰值，一方面增加了翼型升力，另一方面抵消了后加载所附加的低头力矩，使设计翼型保持着良好的低头力矩特性.

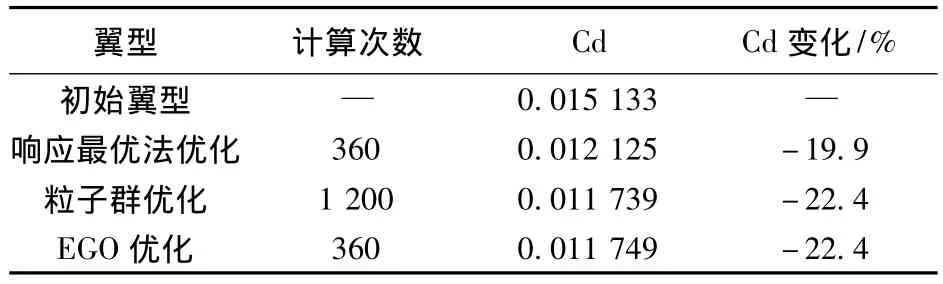
表1 不同优化方法计算次数及优化结果对比

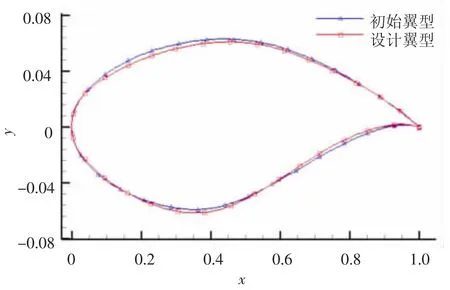
图1 设计翼型与初始翼型形状

虽然构造Kriging模型以及预测气动力需要耗费一定时间，但是与调用气动力计算的耗时相比要小得多，上文算例优化耗时约比粒子群算法减少68%.

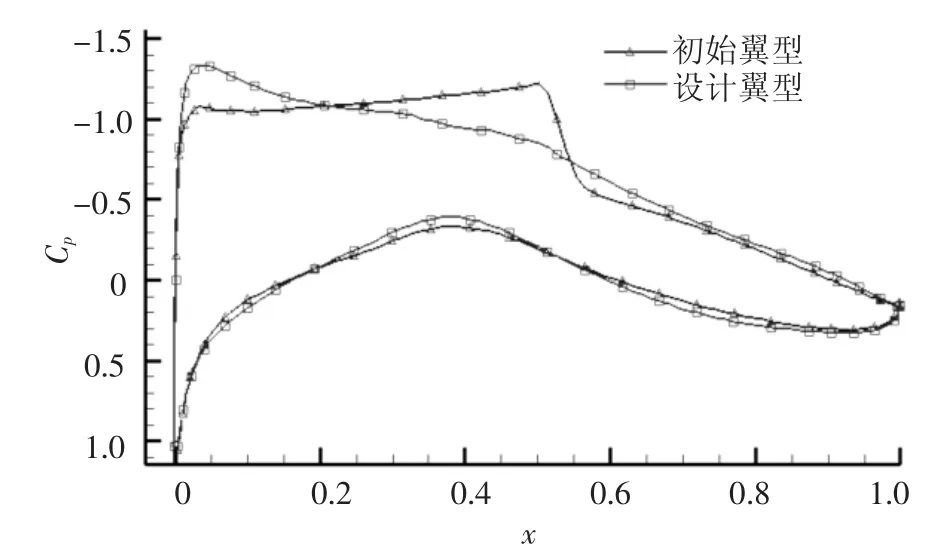
图2 设计翼型与初始翼型压力分布

3 结论

1)本文构建了将Kriging代理模型和粒子群算法相结合的高效优化系统，采用粒子群算法搜索由EI最优策略和响应最优策略交替选择的最优校验点，前者综合考虑代理模型的预测值及预测精度，可以有效避免陷入局部最优，后者可以促使快速收敛.

2)翼型优化设计算例表明本文方法克服了响应最优法容易陷入局部最优的缺点，保证优化精度，同时又有效地减少了计算量，大大提高了翼型气动优化设计的工程实用性.

［1］DUVIGNEAU R，VISONNEAU M.Hybrid genetic algorithms and neural networks for fast CFD-based design［R］.Atlanta:AIAA 2002-5465，2002.

［2］RAJAGOPAL S，GANGULI R.Multidisciplinary design optimization of an UAV wing using kriging based multi-objective genetic algorithm［R］.AIAA 2009-2219，2009.

［3］JONES D L.A taxonomy of global optimization methods based on response surfaces［J］.Journal of Global Optimization，2001，21(4):345-383.

［4］SCHONLAU M.Computer experiments and global optimization［D］.Ontario Canada:Waterloo，1997.

［5］王红涛，竺晓程，杜朝辉.基于Kriging代理模型的改进EGO算法研究［J］.工程设计学报，2009，16(4): 266-270.

［6］苏伟，高正红，夏露.一种代理遗传算法及其在气动优化设计中的应用［J］.西北工业大学学报，2008，26(3):303-307.

［7］KENNEDY J，EBERHART R C.Particle swarm optimization［C］//Proceedings of IEEE International Conference on Neural Networks.Washington，DC:IEEE Service Center，1995:1942-1948.

［8］CRESSIE N A C.Statistics for spatial data［M］.New York:John Wiley＆Sons，1993.

［9］HICKS R M，HENNE P A.Wing design by numerical optimization［J］.Journal of Aircraft，1978，15(7): 407-413.