采用滑块和RSB的太阳帆姿态控制

罗 超，郑建华

(1.中国科学院空间科学与应用研究中心，100190北京，zhengjianhua@cssar.ac.cn;2.中国科学院研究生院，100190北京)

太阳帆航天器是指利用太阳光压力获取推动力进行宇宙航行的飞行器.太阳帆航天器不需要携带燃料，但在太阳光压作用下可以持续加速，最终可达到传统航天器5～10倍的速度，尤其适用于深空探测.由于太阳帆自身的特点使得其姿态控制方法有别于传统空间飞行器，其特点主要有:干扰力矩大，相应的转动惯量也特别大，并且指向精度要求高.由于以上特点，传统的主动姿态控制方法如:喷气控制、反作用飞轮控制等很难满足太阳帆的姿态控制要求，这就需要考虑特殊的适合太阳帆姿态控制的方法.

目前国内外采取的太阳帆控制方案都是利用太阳帆自身特点，由太阳光压力来产生沿某个轴的力矩，进而实现三轴稳定控制［1-3］.按照控制原理可分为两类:质心偏移法、帆面转动法.前者具体有带有两轴万向节的控制杆，在帆面结构杆上滑动的质量块等;后者有滚转轴稳定条、角帆等.

本文采用的是滑块控制结合滚转轴稳定条RSB(Roll Stabilizer Bars)的姿态控制技术.与目前较为流行的采用控制杆的太阳帆姿态控制技术相比，基于滑块和RSB的方案保证了星体与帆的相对位置固定，利于星地通讯;对于太阳帆的展开过程没有特殊要求，保障了太阳帆姿态控制系统的可靠性;而且结构简单，易于制造控制，成本低廉，可靠性高，同时也能够满足太阳帆姿态大角度快速机动的要求.图1即是以滑块和RSB作为姿态执行机构的方形太阳帆.美国亚利桑那大学Bong Wie等［4-5］做了相关的研究.

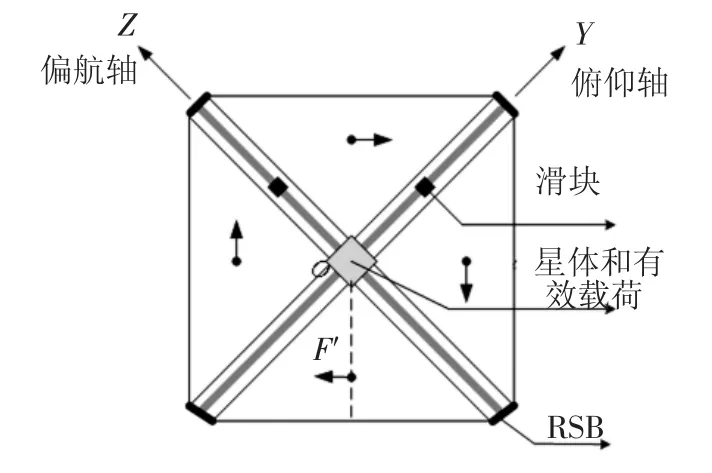
图1 带有滑块和RSB的太阳帆航天器

本文将首先建立太阳帆姿态动力学模型，然后利用非线性PID控制算法设计姿态控制器，并进行数值仿真和分析.最后结合空间中心提出的太阳极轨射电成像仪计划(Solar Polar Orbit Radio Telescope，简称SPORT)，设计适用于该任务的太阳帆三轴稳定姿态控制系统.

1 太阳帆航天器姿态动力学建模

1.1 定义坐标系

以绕太阳运行的太阳帆航天器为例，推导其姿态动力学方程的参考系设定为当地垂直-水平坐标系(LVLH)OXYZ，如图2所示.取航天器质心为坐标系原点O，由O到日心的连线为OZ轴，在轨道平面内与OZ轴垂直并指向前进方向的为OX轴，OY轴和前两轴构成右旋正交系，显然OY轴与轨道平面垂直.

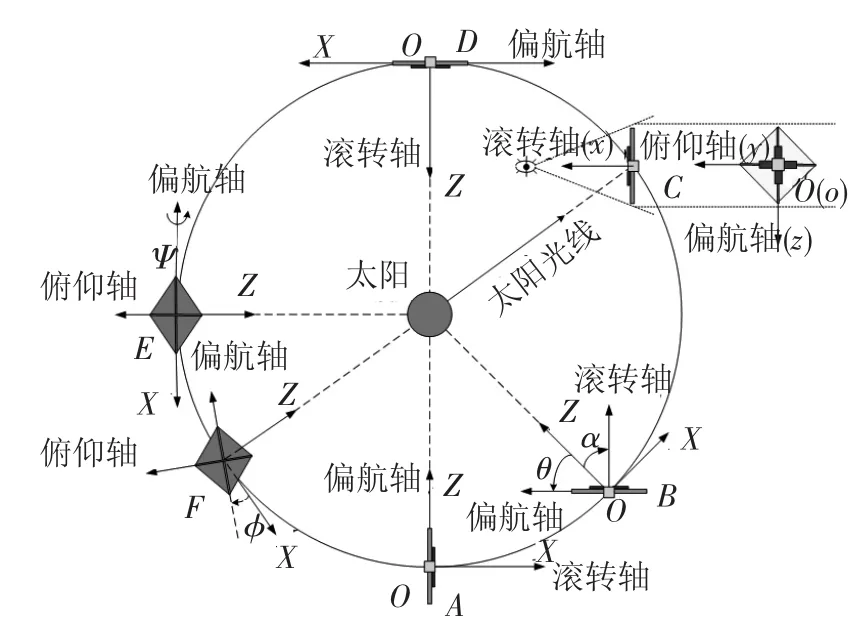
图2 绕日飞行的太阳帆航天器参考坐标系OXYZ和体坐标系oxyz

定义太阳帆体坐标系oxyz，滚转轴(Roll)ox沿帆面法线方向由帆的背光面(E、F处的暗色面)指向帆的反射面(C处的亮色面)，俯仰轴(Pitch)oy、偏航轴(Yaw)oz分别沿结构杆轴向，满足右手定则，见图1中C处.设太阳帆在圆轨道上飞行(为研究坐标系简便，暂不考虑帆的姿态对轨道形状的影响)，在A处，oxyz与OXYZ合，滚转角φ、俯仰角θ、偏航角ψ均为0°，太阳帆处于零照射模式，此时太阳光在帆面上不产生任何力矩，所以一般在这种飞行模式下进行展开太阳帆的动作.由该位置出发，在B处，太阳帆绕俯仰轴负方向转过了ϑ角，太阳光线与滚转轴夹角由90°变为α，太阳光开始在帆上产生控制力矩.从B到D，太阳帆在光压控制力矩作用下，绕俯仰轴负方向转过了90°角，此时太阳光垂直照射帆面，太阳帆处于全照射模式.从D到E，太阳帆绕偏航轴转过了ψ角;从E到F，太阳帆绕滚转轴转过了φ角.

需要注意的是，在A处，太阳帆帆面的光照为零，以太阳光压力为原动力的姿态控制机构失效，所以从A到B的过程中要借助其他姿态控制机构提供的力矩，如小型喷气装置、反作用飞轮等，直到太阳帆转过一定角度，帆上的太阳光压足够大时，才进入本文讨论的姿态控制范围.

1.2 姿态动力学建模

基于滑块和RSB的太阳帆姿态控制原理是:在太阳帆结构杆上运动的滑块用于控制太阳帆航天器的俯仰和偏航通道，即产生绕oy轴和绕oz轴的控制力矩Ty、Tz来分别调节姿态角ϑ和ψ.由于俯仰、偏航和滚转3个通道是耦合的，则利用滑块同时在俯仰通道和偏航通道上进行姿态调整时，必然会引起滚转通道的耦合效应，即绕ox轴的转动.此时为了控制滚转通道的姿态角φ，需要引入沿太阳帆法线方向的控制力矩Tx，RSB的作用就是通过控制帆面的倾斜角度来产生力矩Tx.

1.2.1 滑块控制

由滑块产生控制力矩的原理如图3，以在偏航轴oz上运动的滑块为例.由于制造的误差，太阳帆的质心 c.m.(center of mass)并不与形心——即压心c.p.(center of pressure)重合，而会有1个大小为ε的偏差，以质心O为原点，设压心在质心的正方向上.太阳光压力对帆面的作用效果可以等价于1个施加在c.p.上的力F，当结构杆上没有滑块时，太阳光压将产生1个绕oy轴负方向的干扰力矩Tdy，即

当质量为m的滑块在oz轴上运动时，太阳帆的质心位置就发生了变化.以原质心位置O点为原点，设滑块的位移为z(t)，则质心位置随时间变化的关系式为

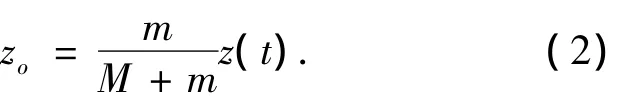
式中M为不包括滑块在内的太阳帆及星体总质量.此时太阳光压产生的力矩为

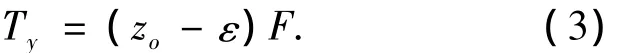
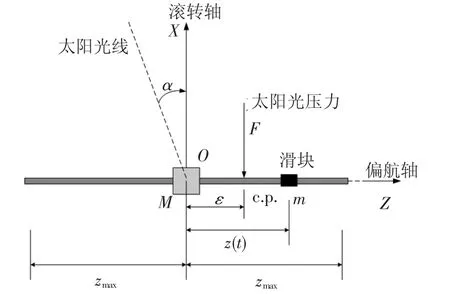
图3 以滑块作为执行机构控制俯仰轴姿态

将式(2)带入式(3)得

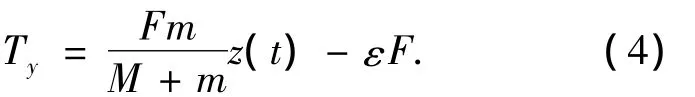
对照式(1)，可知(4)式中的Fmz(t)/(M+ m)项是起控制作用的力矩，该力矩的大小由滑块的质量和滑块在oz轴上的位移决定.

同理，在oy轴上运动的滑块所产生的偏航轴控制力矩Tz可表示为下式:

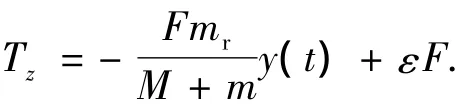
1.2.2 RSB控制

RSB是装在结构杆末端的可以绕结构杆轴转动的机械装置，参见图1，杆末端的4个黑色装置即为RSB.它的工作原理如图4所示.RSB在接到转动指令Θc后，转过Θ角，从而带动帆面倾斜了χ角，太阳光压力就会在倾斜了的帆面上产生大小为F'的分力.在控制帆面的运动时，4个RSB同时转动，且转动的方向和角度均一致，因此4片三角形帆倾斜角度始终能够保持一致，太阳光压在4片帆上产生的分力恰为2对共面力偶.这2对力偶共同产生了沿帆面法线方向的力矩Tx，即滚转轴控制力矩.

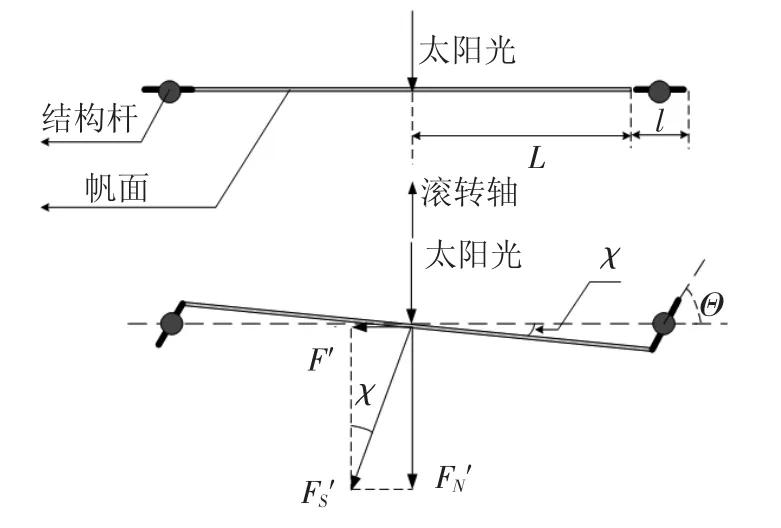
图4 RSB的工作原理

由于每片帆都是等腰直角三角形，Tx可由下式得到

由图4可知，设太阳光垂直照射帆面，则有F'=F'Ssin χ=F'Slsin Θ/2L，又有F'S=FS/4，代入式(5)得

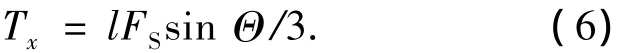
其中FS为太阳帆受到的总光压，由下式得到:

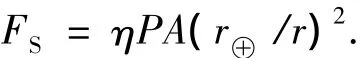
式中:η称为太阳帆推进系数，对于理想的太阳帆，ηmax=2，通常取η=1.8较符合实际情况; p=4.563×10-6N/m2为地球附近的光压系数;A是帆的有效反射面积;r⊕为地球到太阳的距离;r为太阳帆航天器到太阳的距离.当太阳光线与帆面法线夹角为α时，式(6)变为

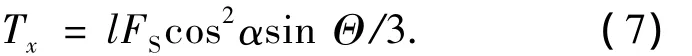
式(7)即为利用RSB控制滚转轴转动的力矩计算公式，可见力矩大小由RSB杆的长度及转过的角度决定.本质上该力矩是由太阳光压产生的，所以其大小还和太阳光压及照射角有关.

1.2.3 太阳帆姿态动力学方程

基于滑块和RSB控制的太阳帆姿态动力学方程可由下式表示:

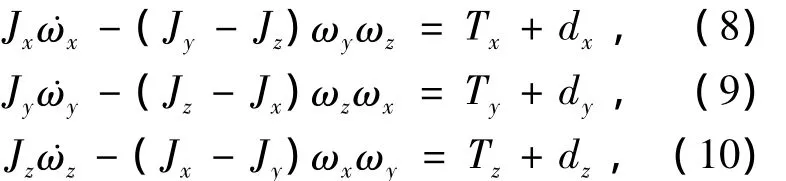
式中，Jx=Ix+mr(y2+z2)，Jy=Iy+mrz2，Jz=Iz+mry2，(Ix，Iy，Iz)是帆体的主转动惯量. mr为折合质量，可由下式得出:

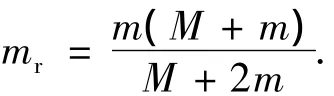
当M≫m时，mr≈m.Tx、Ty、Tz分别是3个轴的控制力矩，dx、dy、dz为干扰力矩.

将滑块和RSB的力矩计算公式代入式(8)～(10)中，并假设滚转轴受到的太阳光压干扰力矩为俯仰/偏航轴的50%，得到了以地球为中心引力体运行的太阳帆航天器的姿态动力学方程［6-7］，即

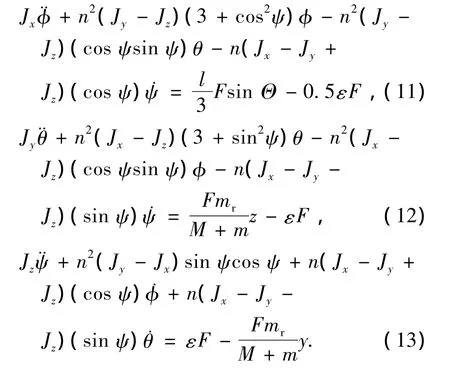
当太阳帆航天器以太阳为中心引力体飞行时，如中科院空间中心提出的SPORT任务(Solar Polar Orbit Radio Telescope)、美国NASA/JPL提出的SPI任务(Solar Polar Imager Mission)等，其轨道高度至少在0.5 AU之上，此时可以不考虑重力梯度力矩的干扰，由质心形心差引起的太阳光压干扰力矩是主要干扰项.

2 太阳帆航天器姿态控制器设计

太阳帆航天器的姿态控制多是机动控制，通常要求太阳帆姿态在短时间内机动较大角度，本文采用的姿态控制算法是适合大角度快速机动的非线性PID控制法［8］.相比较经典PID控制，非线性PID控制更加适合处理非线性系统问题，而且选取参数的方法也比较简单.

2.1 滚转轴(x轴)的控制器设计

滚转轴的姿态动力学方程可由式(11)简化为

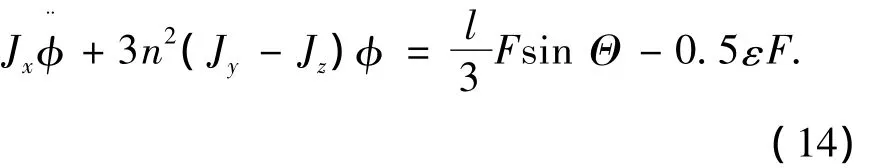
RSB的运动学方程如下:

式中:T为时间参数，Θc为RSB的控制指令，由下式得到

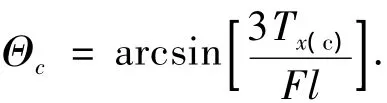
分析式(14)，单独控制x轴时，为了使控制简单，可以让y、z轴上的滑块保持在合适位置以使Jy=Jz.此时x轴的控制模型可以更简化为

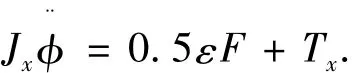
滚转轴姿态控制力矩指令Tx(c)由非线性PID控制算法设计为如下形式:

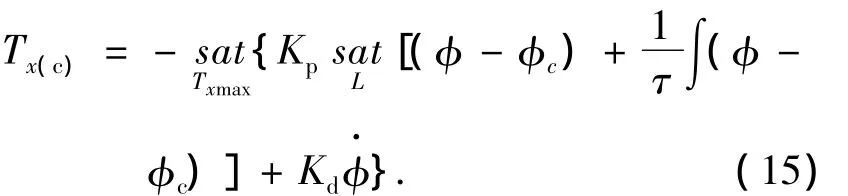
令e=φ-φc，Kp、Kd分别是姿态角和姿态角速度的增益参数，τ是积分环节参数，饱和函数定义如下:

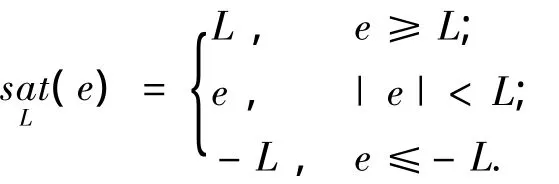
即，

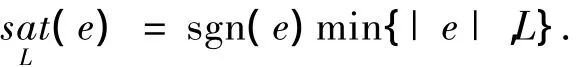
阈值L由下式选取:

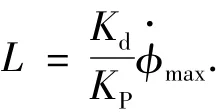
绕x轴旋转的角速度最大值 ˙φmax可定义为下式:

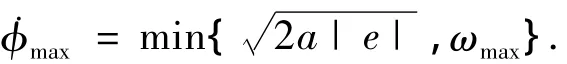
式中，ωmax是设计允许的最大角速度，a为最大角加速度，且

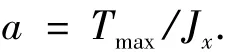
滚转轴姿态控制器式(15)中参数设计方法为

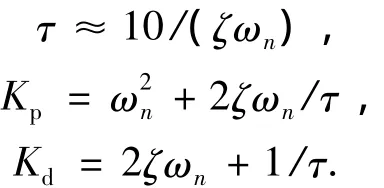
可见实际需要设计的参数只有控制器阻尼ζ和x轴预期转速ωn，式(15)中的各参数就能确定下来，从而得到滚转轴的控制力矩指令Tx(c).

2.2 俯仰轴(y轴)的控制器设计

由式(12)简化后的y轴姿态动力学方程为

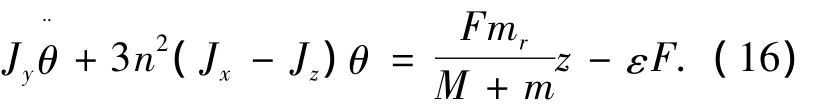
滑块的稳定位置zss由下式得到

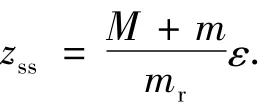
滑块的运动学方程如下

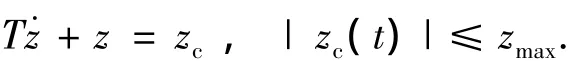
式中:T为时间参数，zc为滑块的控制指令，它由控制力矩指令Ty(c)决定，

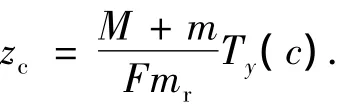
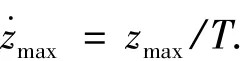
y轴姿态控制力矩指令Ty(c)设计为如下形式:

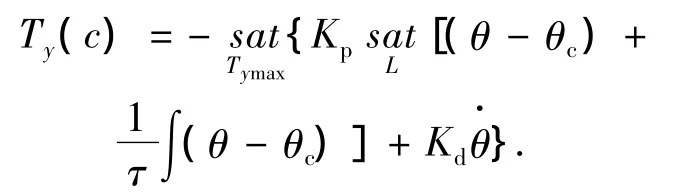
式中各参数物理意义及选择方法同x轴.

2.3 偏航轴(z轴)的控制器设计

偏航轴的控制器设计与俯仰轴相似，其控制力矩由在oy轴上运动的滑块产生.由式(13)简化后的z轴姿态动力学方程为

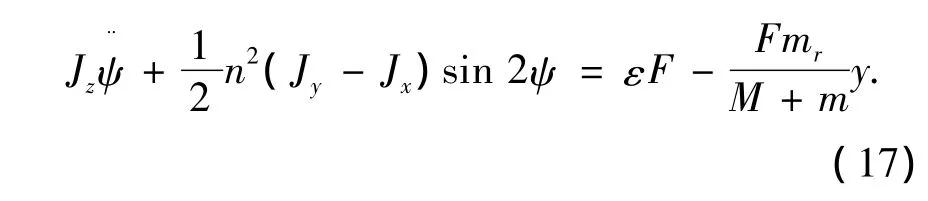
z轴姿态控制力矩指令Tz(c)设计为

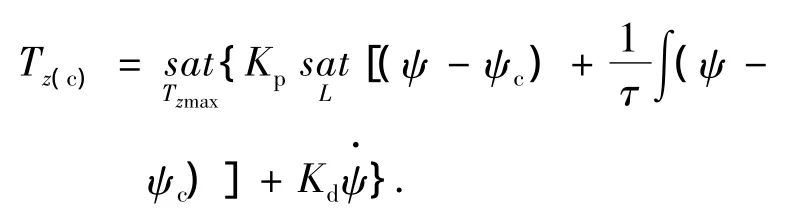
相应的滑块位置指令yc由下式得到:

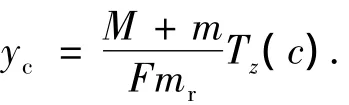
3 数值仿真和分析

采用按上述方法设计的太阳帆非线性PID姿态控制器，针对式(14)、(16)、(17)表述的简化后的非线性姿态动力学模型，进行数值仿真.表1是阿连特技术系统(ATK)公司研制的太阳帆的结构参数［5］，160 m级的太阳帆适合绕日飞行任务，如SPORT计划、SPI任务等.

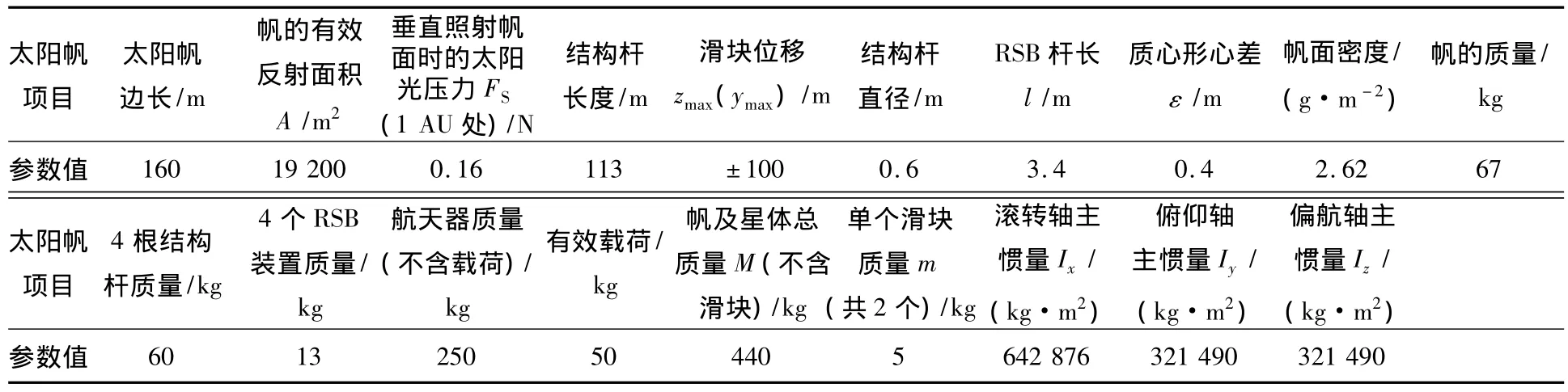
表1 160 m级的方形太阳帆结构参数表

3.1 太阳帆航天器参考输入短期响应测试

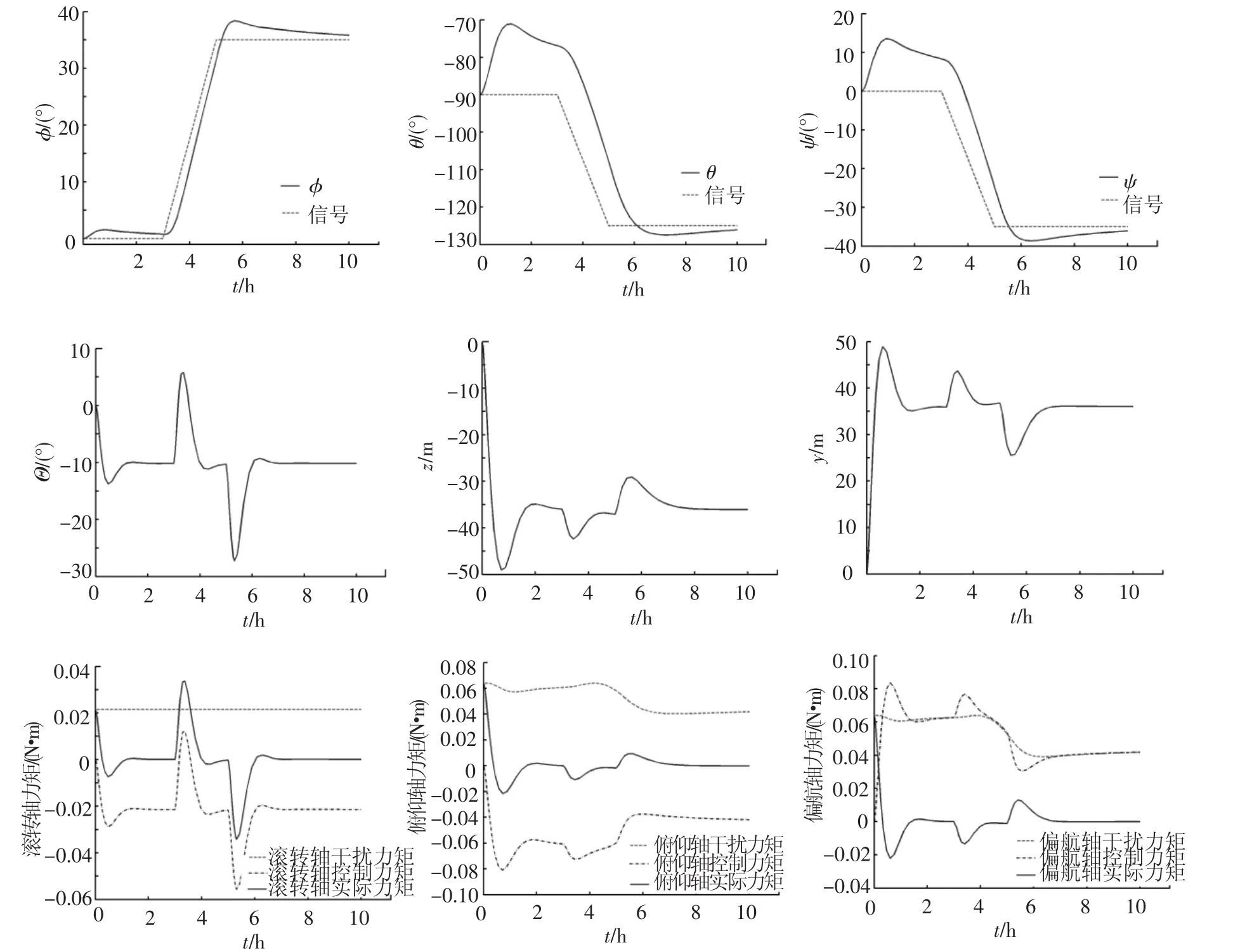
图5 三轴参考输入皆为斜坡信号时的系统响应

设太阳帆初始姿态角为(0°，-90°，0°)，即太阳帆处于全照射模式下(图2的D处)，轨道半径为1 AU.在短期响应测试中，使用斜坡信号作为参考输入分别对3个轴的姿态控制系统进行测试.系统响应过程如图5所示.输入始于3 h，由三轴姿态角的响应来看，过渡过程时间在8 h左右.在0时刻，执行机构RSB、滑块均处于零位，控制力矩为零，3个轴在干扰力矩作用下发生转动，偏离了初始位置.此时姿态控制系统开始工作，在控制指令作用下，RSB和滑块向期望位置运动，从而产生控制力矩，控制3个轴稳定到初始姿态角.滚转轴的干扰力矩大小只有俯仰/偏航轴的一半，因此滚转角φ偏离初始角的幅度最小.

在斜坡信号开始作用后，三轴的姿态角迅速跟踪参考输入至稳定值.整个过程中，RSB转角峰值只有-27.3°，距离极限位置±45°有较大的裕度，φ角响应的超调得到显著改善.俯仰/偏航轴上的滑块位移变化平缓，峰值显著减小.3个轴的控制力矩峰值分别为 -0.055 6、-0.080 9、0.083 7 N·m.仿真结果表明，在太阳帆姿态控制中，如果始终保持参考输入为震荡较小的信号，则系统响应将会非常平缓.

3.2 SPORT任务中轨道转移段的太阳帆姿态控制

SPORT计划要求探测器脱离黄道面进入太阳极轨，从黄道面的上方(或下方)居高临下地遥感观测日冕物质抛射(CME)的传播和演化，并对其进行成像.探测器运行轨道为太阳极轨轨道，近日点rp=0.5 AU，远日点ra=1.5 AU，轨道倾角i=90°，近心点角距ω=270°(远日点设在太阳北极附近).

利用太阳帆推进技术实现SPORT任务要求的目标轨道的完整飞行轨迹如图6所示，从脱离地球影响球(展开太阳帆时)到实现任务目标轨道，共耗时7.1 a.实际达到的目标轨道(图中粗实线)描述如下:半长轴a=1.000 2 AU，偏心率e=0.480 62，近心点rp=0.519 5 AU，远心点ra=1.481 0 AU.轨道倾角i=89.968°，升交点黄经24.014°，近心点角距ω=271.17°［9］.

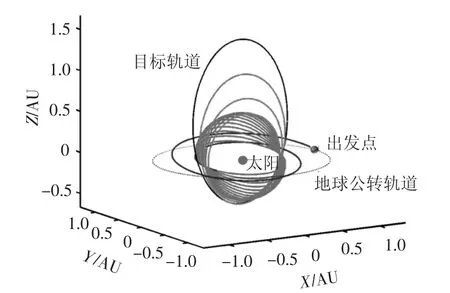
图6 利用太阳帆实现SPORT任务目标轨道仿真

在整个飞行过程中，太阳帆航天器的轨道转移大致可分为3个阶段:1)内螺旋轨道转移阶段;2)轨道倾角抬升阶段;3)轨道椭化及近心点角距调整阶段.相应的姿态调整规律以太阳帆控制角α、δ的形式表示为为atan(-360).α的输入保持，即35.26°.

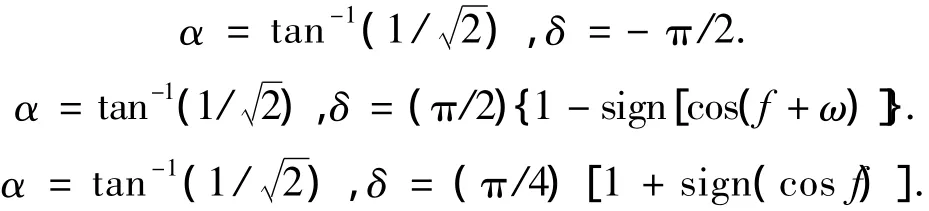
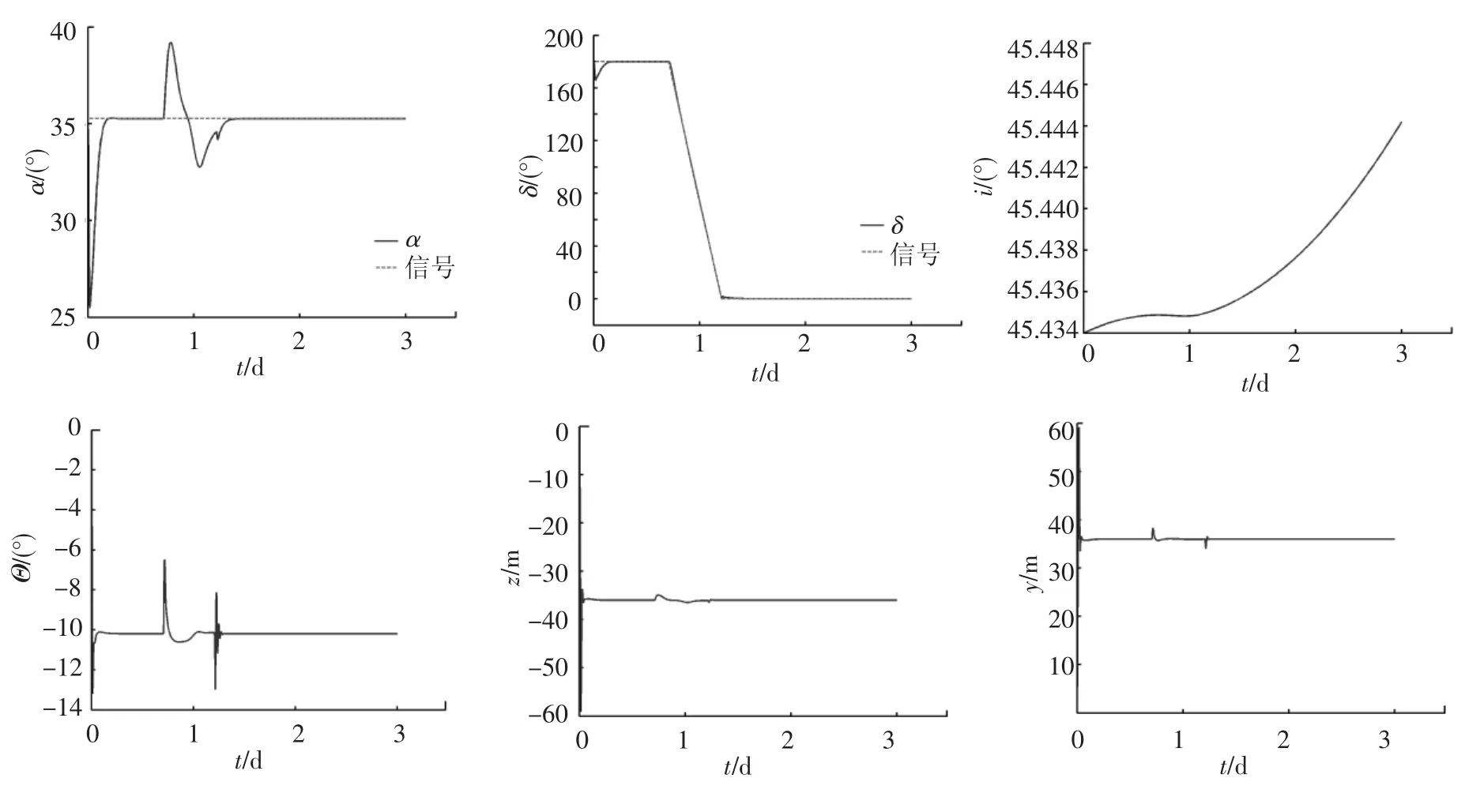
图7 太阳帆轨道倾角抬升阶段的姿态调整仿真

Bong Wie［4］给出了α、δ与姿态四元素的转换关系，本文以轨道倾角抬升阶段(该阶段姿态调整频繁且姿态变化幅度最大)的姿态调整为例，对处于轨道转移阶段的太阳帆姿态控制进行仿真试验.仿真结果见图7，为保证姿态控制过程不出现较大震荡，δ的输入为斜坡信号，信号斜坡斜率

从图7可看出，太阳帆控制角α、δ能非常好地跟踪输入信号，在较短时间内实现了姿态的大幅度调整，轨道倾角抬升速率为0.003 3(°)/d (整个轨道抬升阶段平均速率为0.051(°)/d). RSB转角峰值和滑块位移峰值都距离极限位置有较大裕度.仿真结果表明，该姿态控制系统能够满足太阳帆轨道倾角抬升段的姿态调整要求.

4 结论

通过本文的研究表明，基于滑块和RSB控制的太阳帆航天器三轴姿态控制技术，能够满足太阳帆航天器姿态在短时间内调整较大角度的要求，从而实现相应的轨道转移;由滑块移动和RSB转动产生的控制力矩较小，实现了姿态的精确控制.文中采用的非线性PID控制算法简单有效，据此设计的控制器能够完成太阳帆姿态控制的任务.

与带有控制杆的方案相比较，基于滑块和RSB控制的太阳帆航天器三轴姿态控制技术具有更大的实际应用价值，在未来的太阳帆航天器研究中将有广阔的应用前景.

［1］WIE B.Dynamic modeling and attitude control of solar sail spacecraft:Part I，II［C］//AIAA Guidance，Navigation，and Control Conference and Exhibit.Monterey:［s.n.］，2002，AIAA-2002-4573.

［2］METTLER E，PLOEN S R.Attitude dynamics and control of solar sails with articulated vanes［C］//AIAA Guidance，Navigation，and Control Conference and Exhibit.Pasadena，CA:Jet Propulsion Laboratory，National Aeroncutics and Space Administration，2005，2005-6081.

［3］崔祜涛，骆军红，崔平远，等.基于控制杆的太阳帆姿态控制研究［J］.宇航学报，2008，29:170-176.

［4］WIE B.Thrust vector control analysis and design for solar-sail spacecraft［J］.Journal of Spacecraft and Rockets，2007，44(3):545-557.

［5］WIE B，MURPHY D.Solar-sail attitude control design for a sail flight validation misson［J］.Journal of Spacecraft and Rockets，2007，44(4):809-821.

［6］刘暾，赵钧.空间飞行器动力学［M］.哈尔滨:哈尔滨工业大学出版社，2003:165-172.

［7］章仁为.卫星轨道姿态动力学与控制［M］.北京:北京航空航天大学出版社，1998:265-268.

［8］WIE B，MURPHY D，HEIBERG C.Rapid multi-target acquisition and pointing control of agile spacecraft［C］// AIAA Guidance，Navigation，and Control Conference and Exhibit.Denver，CO:［s.n.］，2000，AIAA-2000-4546.

［9］罗超，郑建华，高东.太阳帆航天器的轨道动力学和轨道控制研究［J］.宇航学报，2009，30:2111-2117.