薄膜加载变形的有限元数值优化反演求解

石广丰，刘丽萍，袁帅

（1.长春理工大学，长春 130022；2.长春职业技术学院，长春 130033；3.中国专利信息中心，北京 100088）

薄膜反射镜技术是解决空间望远镜主镜大口径、轻量化问题的主要手段，而利用静电成形法是薄膜反射镜成形的革命性控制方法［1］。但是，反射镜聚合物薄膜的超柔、低刚度特点使得薄膜反射镜的面形控制受到极大的挑战。目前由已知薄膜加载条件，求薄膜变形（正演求解）的问题广泛研究，已有很多成果［2］。多电极静电薄膜反射镜面形控制的核心问题就是由已知目标面形（一定面形精度的抛物面）反求初始平面状态下的薄膜受载性质［3］，这属于薄膜加载变形的反演求解问题。

1978年国外的D.J.Mihora给出了薄膜反射镜的反演数值解法［4］，但具体内容未见报道。1986年E.S.CLAFLIN和N.BAREKET给出了基于泊松方程小变形理论的最小二乘法解析求解方法［5］。2004年JéromeJuillard和MihaiCristescu在已知目标面形的前提下，求VonKarman方程的解析解［6］。在国内，浙江大学的徐彦通过求解变形前后的薄膜力学平衡微积分方程方法在均布载荷作用下以抛物面为目标面反演求解了初始面形和载荷大小［7］。从国内、外的现状分析可知，目前关于薄膜加载变形的反演求解问题研究的并不多。

本文建立了薄膜加载变形的有限元数值优化反演求解模型，并通过 ANSYS有限元仿真软件的APDL参数化语言编制了优化求解程序，对一定预张力条件下的薄膜受载性质和面形之间的关系进行了研究，对于薄膜反射镜的非均布载荷成形控制具有重要意义。

1 反演求解

1.1 优化算法

由薄膜受载变形的正演求解问题，我们可以求出薄膜在一定预张力［8］条件下受均布载荷所得的变形值。若将这个变形值条件下的抛物面面形作为目标，反演求解所需的离散均布载荷的大小，可大大减少数值迭代计算的次数和时间。即薄膜加载变形的正演问题为反演求解问题提供了计算的基础（如图1）。算法如图2所示。

图1 薄膜受载变形的求解方法Fig.1 Solution methods of membrane pressed to deform

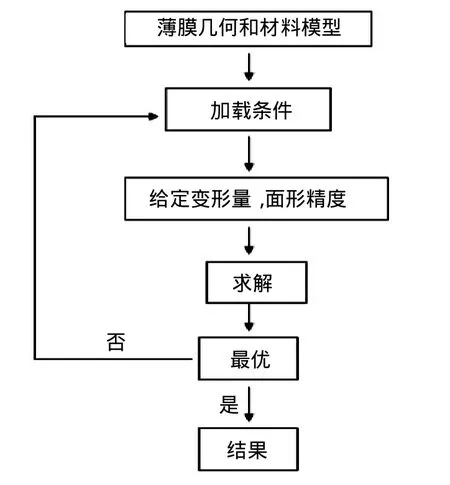
图2 薄膜加载变形反演求解算法Fig.2 Algorithm of inverse solution about membrane forced to deform

下面介绍一下在有限元分析软件ANSYS环境中利用其APDL程序语言建立薄膜加载变形反演求解的参数化求解模型。

1.2 有限元求解模型

（1）薄膜区域加载

以6 mm 的单元大小对［9］300mm口径、25m厚的聚酰亚胺薄膜进行划分，结点数2276，有限元模型如图3和4所示。薄膜材料属性如文献［3］。从表1可以看出均压条件下薄膜中心变形量数值和Hencky-Campbell薄膜大变形级数解析解［10］在小数点后三位是相同的，可见程序的正确性。

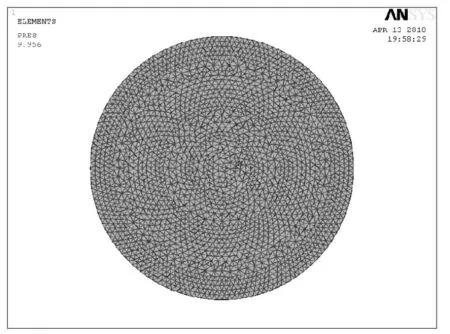
图3 薄膜有限元模型Fig.3 Finite element model of the membrane

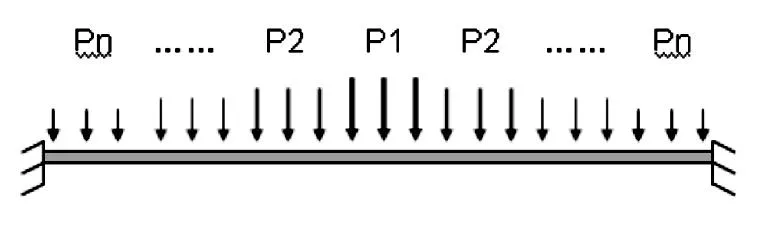
图4 分区均布加载形式Fig.4 Style of discrete equal pressures exerted on the membrane

外界的温、湿度变化会对薄膜的面内张力产生影响，根据薄膜热膨胀系数与热张力的关系，薄膜预张力为［9］

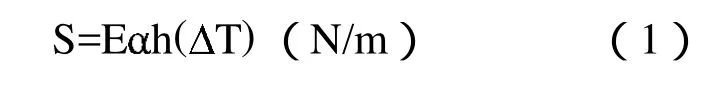
根据式（1），可以在模拟环境中通过采用降温的方法来模拟薄膜边界预张力的变化。

表1 一定边界条件下的薄膜受载变形对比Tab.1 Contrast of membrane deformation under certain boundary condition and pressure

（2）面形目标提取

薄膜成形面形和理想面形偏差的均方根是评价面形质量的重要手段。将结点坐标值和结点变形值相加，得到变形后的结点坐标。在轴截面内可由两个固定边界点和中心变形点确定理想抛物线。由计算面形和理论面形对应结点的坐标偏差RMS可反映迭代计算的优化目标。

（3）面形优化

在确定优化目标之后，将离散均布载荷分别作为变量进行全局优化，计算面形和理论面形中心变形量偏差和薄膜极限拉伸强度作为状态变量，可实现一定边界预张力和薄膜材料模型条件下薄膜成形所需的离散优化载荷大小。

2 求解分析

为了分析离散环形均布载荷的多少对优化面形的控制作用，利用上面的求解模型得到了薄膜分别在变形中心变形量为0.5mm、1mm和1.5mm三种情况下的载荷多少与所得薄膜面形精度之间的关系。从图3中可以发现当划分载荷等径宽区域的数目超过3以上时，薄膜的面形精度区域稳定。因此可以利用三环离散均布载荷来进行面形控制的优化分析。

图3 优化面形偏差RMS随等径宽分区载荷环数变化的关系Fig.3 Relation between optimized surface RMS and the annulus number change of equal pressures exerted on membrane in the radial direction

采用三环等径宽载荷作用区域对薄膜进行不同预张力条件下的优化载荷加载变形求解。从表2-表4中可以看出：

（1）当预张力相同的条件下，非均布优化载荷可使面形精度显著提高；但随着均步载荷的增大，非均压优化面形的精度下降，即在已有控制条件下，小变形的面形精度高，薄膜变形越大，面形越差。

（2）预张力越大，薄膜面形优化后的精度也越大，预张力增大所提高的面形精度和薄膜非均布优化所得的面形精度相当。

（3）薄膜变形量越小，薄膜面形的均压和优化非均压的面形精度之间优化幅度越小；薄膜变形量越大，薄膜面形的均压和优化非均压的面形精度优化幅度越大，优化非均布电压之间差值也越大，优化面形对比分析明显。当预张力增大时，薄膜面形的均压和优化非均压的面形精度之间的优化幅度降低。

（4）虽然优化后的面形精度得到提高，薄膜中心变形量却有一定偏差。可以缩小薄膜中心变形量偏差状态变量来达到精确矢高控制的目的，但会牺牲部分面形精度。因此应当合理设置薄膜中心变形量偏差状态变量和面形目标优化精度，获得所需面形的控制目的。

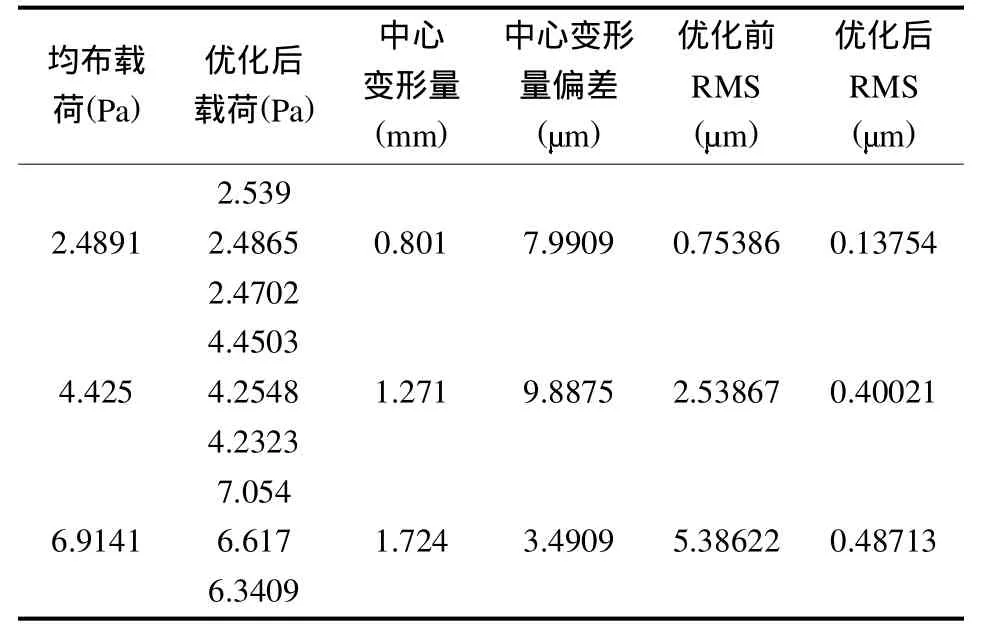
表2 对应降温-6.7538℃时的优化加载和面形关系Tab.2 Relation between optimized pressures and precision of membrane surface at the changed temperature of-6.7538℃

表3 对应降温-15.1751℃时的优化加载和面形关系Tab.3 Relation between optimized pressures and precision of membrane surface at the changed temperature of-15.1751℃

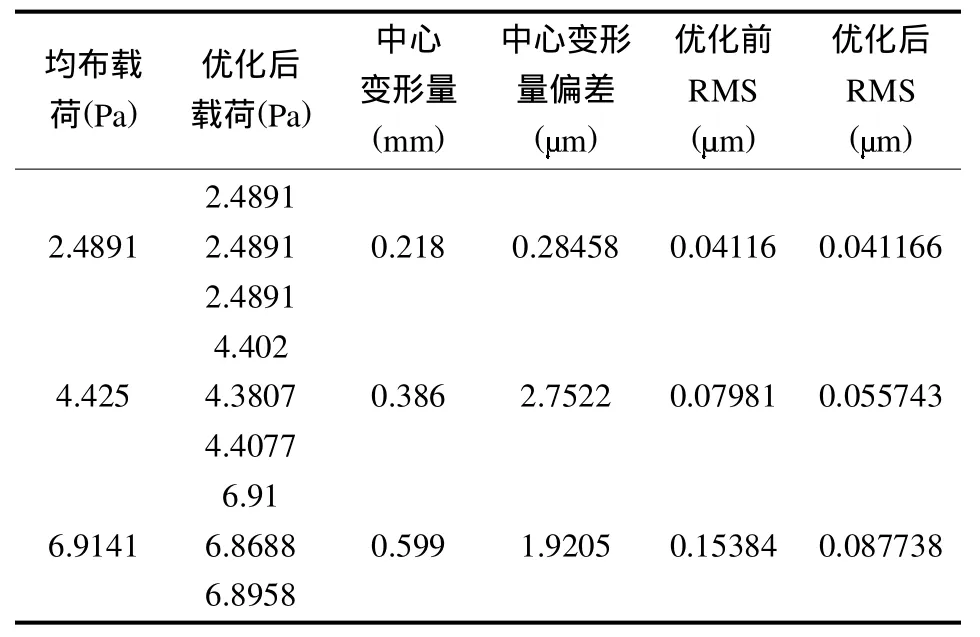
表4 对应降温-26.9262℃时的优化加载和面形关系Tab.4 Relation between optimized pressures and precision of membrane surface at the changed temperature of-26.9262℃

通过此反演求解模型可以初步分析出薄膜预张力、离散均布优化载荷和面形精度和矢高之间的影响关系，找到了面形离散均布载荷控制的依据。

3 结论

给出了以一定面形精度和中心变形量的抛物面为目标的柔性平面薄膜加载变形的反演求解算法和有限元模型。通过对300mm口径、25um厚的聚酰亚胺薄膜三环等径宽离散均布载荷的反演优化求解，分析了薄膜边界预张力和优化载荷对薄膜面形精度和矢高的控制规律和特点。在薄膜边界预张力一定的情况下，薄膜面形精度由优化载荷和变形矢高决定；对于大变形的薄膜面形控制，在施加优化载荷的同时，提高薄膜边界预张力可有效提高薄膜面形精度。

本文工作为薄膜反射镜的大变形高精度面形控制研究奠定了理论基础。

［1］石广丰，金光，张鹏.静电薄膜反射镜的关键技术研究［J］.长春理工大学学报：自然科学版，2009，32（4）：592-638.

［2］齐迎春.空间薄膜反射镜的成像机理研究［D］.中国科学院研究生院，2007.

［3］石广丰，金光，刘春雨，等.薄膜反射镜成形控制［J］.光学精密工程，2009，17（4）：732-737.

［4］Mihora D J，Stresses in adaptive membrane reflector［C］.Eighth U.S.National Congress of Applied Mechanics，University of California at Los Angeles（UCLA），1978，6.

［5］Claflin E S，Bareket N.Configuring an electrostatic membrane mirror by least squares fitting with analytically derived influence functions［J］.Opt Soc Am，1986，3（11）：1833-1839.

［6］Jérome J，Mihai C.An inverse approach to the design of adaptive micro-mirrors［J］.J Micromech Microeng，2004，14：347-355.

［7］徐彦，关富玲，马燕红.充气可展天线的反射面设计及精度测量［J］.浙江大学学报：工学版，2007，41（11）：1921-1926.

［8］石广丰，金光，张鹏，等.边界位移调节量对薄膜反射镜成形的影响［J］.半导体光电，2010，31（3）：402-405.

［9］齐迎春，金光，许艳军.空间薄膜反射镜面形设计及优化［J］.光学精密工程，2007，15（6）：818-823.

［10］Campbell J D.On the theory of initially tensioned circu lar membrane subjected to uniform pressure［J］.Quart J Mech，1956，4：84-93.