准绝对式距离码编码器的研究

盖竹秋

（1.中国科学院 长春光学精密机械与物理研究所，长春 130033；2.长春理工大学，长春 130022）

光电轴角编码器是一种数字式测角装置，它把轴角信息转换成数字代码，与计算机系统连接后可实现角度信息的动态测量和对系统姿态的实时控制。随着科学技术的进一步发展，人们对深空探测设备、高精度雷达、数字经纬仪等仪器设备的测量、定位精度提出了更高的要求，高精度的角度传感器是这些仪器的关键部件，它的定位精度的提升对整机性能的提高起到了关键性的作用。尤其在一些大型军用设备和高技术装置中得到了更为广泛的应用。

国内高精度的绝对式编码器，目前还是采用60年代技术，即在圆盘平面内光刻上同心环（码道），并行读出格雷码，输出的位数越高码道数越多，高精度码盘码道数为二十三圈，它占用了轴端面很大的尺寸。为了减少码盘码道数，80年代研发了矩阵式绝对式编码器，码道数减少仅1/4。

为提高测角的精度，一味的增加码道数，势必受到码盘尺寸的限制，对码盘的刻划工艺和信号的提取技术都提出了相当高的要求，不易实现。因此提出采用距离编码的方案，在不损失测角精度的前提下以减小码盘尺寸为目的开发新的准绝对式编码方法，并以此为基础为基地大型光电经纬仪开发高精度角位移测量技术，也可为天基观测设备提供超小型、高分辨率的角度测量技术，为实现工程应用开展前期预研工作具有重要的意义。

1 距离码编码的工作原理

码盘是编码器的核心部件，它是一块具有若干同心码道的玻璃或金属圆盘，每条码道由若干透明与不透明相间的线条构成，每条码道的线条宽度及码道线条间的相互位置按一定规律排列，以满足编码器输出码制及分辨率的要求。常见的有绝对式码盘和增量式码盘两种。绝对式编码器直接输出位置的绝对值，但是由于码道多，尺寸大，电路处理复杂；增量式编码器输出的是上电时刻的相对位置，要输出绝对位置，必须寻到唯一的一个零位标记点。

准绝对式编码器采用距离码码盘。它是兼顾绝对式和增量式码盘特点的一种新型编码方式，仅有两圈码道，一圈为增量圆光栅，另一圈为标记不同角距离的标记点N，相邻标记点的距离在全周的位置是单一的，它将测角分成了N个区，通过移动扫描两个相邻标记点间的距离，则可读出区，从而判断出码盘绝对位置。如图1所示为距离码码盘图案示例：

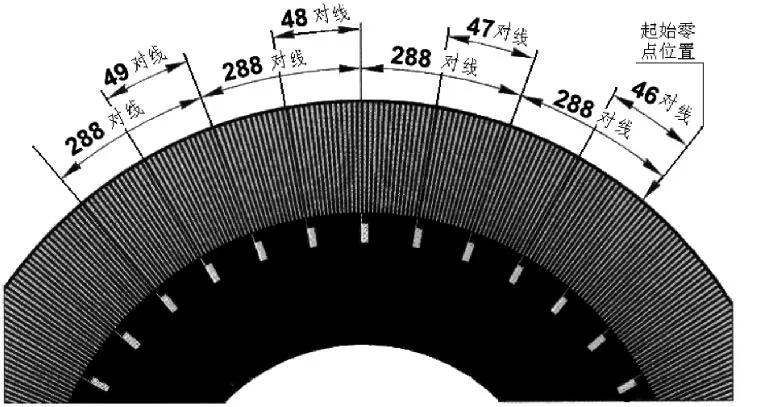
图1 距离码码盘示意图Fig.1 Schematic diagram of interval encoder

其中外圈为主光栅，整周刻线为28800对线，内圈为200个零位标记点，标记点将主光栅分成100个区（N=100），每个区为288对线。距离码编码方案码道少，电路处理简单，可靠性高。N值越大，移动扫描的距离越小。输出绝对角度位置所需要转动的角度越小。

2 码盘信号的提取与译码实现

2.1 码盘信号的提取

采用刻划中径为137mm，光栅密度为28800对线的高密度光栅，光栅节距14.9m。整周编制200个绝对零点，距离最近的两个零点圆周距离为0.6mm。常规的零点信号提取方法无法避免距离很近的两个零点信号的相互影响。采用单刻线零点提取方法，刻线宽度为增量光栅节距的一半，采用激光聚焦照亮单缝刻线的方法，提取宽度适宜的绝对零点信号。

准绝对式距离码编码器结构如图2所示。

由光源发出的光线经过光学系统后变成平行光，平行光透过码盘和指示光栅（指示光栅也称作狭缝）。当码盘与指示光栅产生相对运动时，将透过的光线切割成强弱变化的莫尔条纹光信号，经光电接收器转换成相位相差90°的G0、G90、G180和G270四路电信号。这些电信号包含了转动轴与不动基础间的相对角度位移信息，如图3所示，这些信号由电路系统采集，并经过软件计数，莫尔条纹的电子学插值细分，校正处理等环节得到二进制角度代码输出。

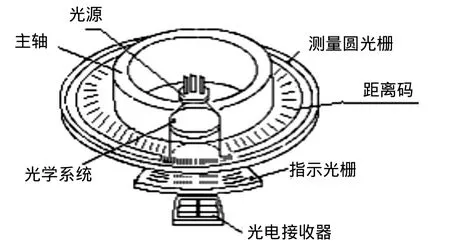
图2 准绝对式编码器结构图Fig.2 Structure of semi-absolute encoder

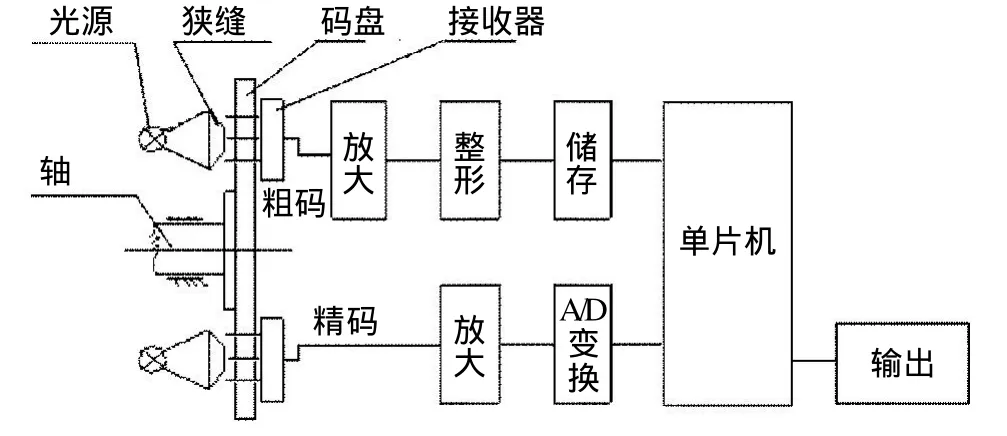
图3 码盘信号处理原理图Fig.3 Schematic diagram of sampling encoder's signals

2.2 距离码译码

由图1可看出，两个相邻零位点之间的主光栅线对数是不同的，当读数头扫描两个相邻零位标记点时，通过判断相邻标记点之间的主光栅脉冲数可以断定码盘的绝对位置。所以在硬件设计上需要既要实现获取零位点的到来时刻，同时又要有计数逻辑电路来记录主光栅的脉冲数，在软件中编制位置表确定当前的绝对位置。

如图4所示，接收器输出的相位相差90°的G0、G90、G180、G270四路信号经过差分放大形成SINQ和COSQ两路正弦信号，经过计数逻辑单元，对SINQ脉冲采用软件中断方式进行计数；同时，将另一路脉冲信号COSQ送入单片机，根据信号的状态判断编码器的旋转方向。

当编码器正向旋转时，其计数原理如图 5所示，每当单片机进入中断计数的时候，SINQ和COSQ 要么同为“+”，要么同为“-”，即 SINQ和COSQ的高低电平状态总是相同：

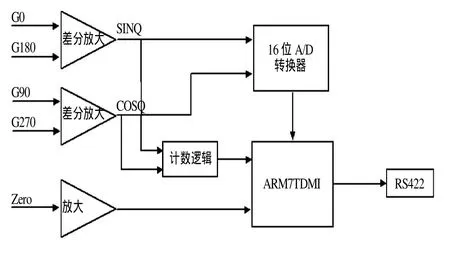
图4 脉冲计数处理示意图Fig.4 Schematic diagram of counting impulse

图5 正转计数原理Fig.5 Schematic diagram of counting while rotating clockwise

当编码器反向旋转时，其计数原理如图 6所示：每当单片机进入中断计数的时候，SINQ和COSQ一个为“+”，另一个为“-”，即SINQ和COSQ的高低电平状态总是相反：

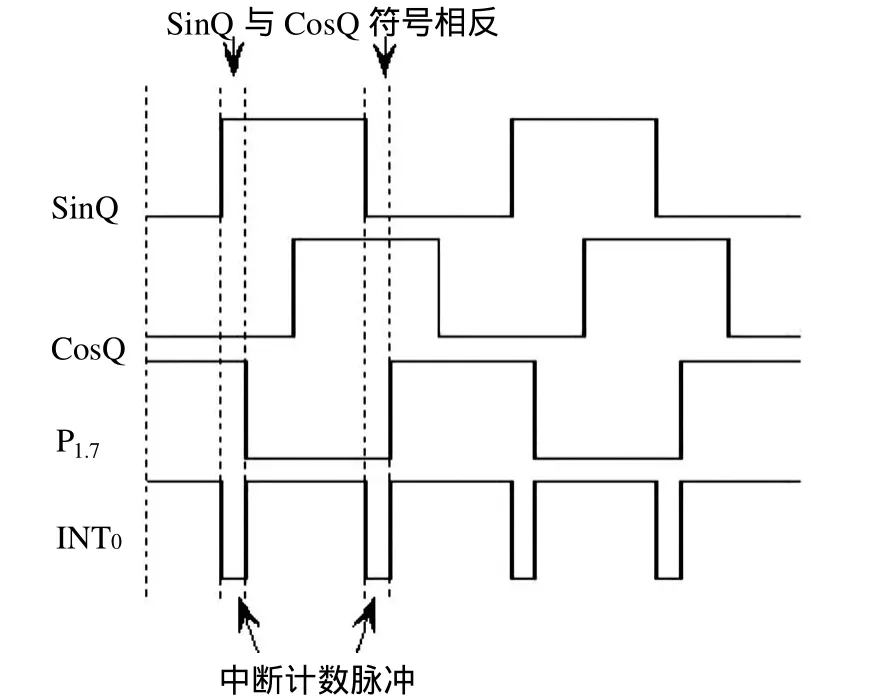
图6 反转计数原理图Fig.6 Schematic diagram of counting while rotating counter-clockwise

通过以上的计数方法，很容易确定两个相邻标记点之间的主光栅的脉冲数，从而确定角度的绝对位置。再将SINQ和COSQ两路正弦信号通过A/D转换器采集到单片机，进行软件电子学插值细分，细分8192份，可得到更高的角度分辨力，提高角度传感器的探测能力。由公式（1）可以得出：角度分辨力约为0.005″。

3 测量实验与结果

3.1 实验方案

根据传感器的特点，采用对径相加数据采集系统，以消除码盘偏心和轴系晃动对测角精度的影响，系统原理如图7所示。

图7 数据处理系统原理图Fig.7 Schematic diagram of data processing system

角位移传感器由4个读数头组成，每个读数头都包括4路相位互差90度的正弦信号及零位标记点信号，这四个读数头分别由4块独立的电路处理系统完成编码功能，并通过RS485串口将数据发送给PCI板卡，PC机数据处理系统通过PCI总线读取4个头的数据，进行对径数据相加技术，完成具有0.005″分辨率的角度编码。

四个读数头的电路处理系统是相同的。具有ARM7TDMI核的微处理器对量化后的数据进行电子学插值细分处理，细分出8192份；同时，差分放大后的两路信号 SINQ、COSQ在计数逻辑单元中经过整形，送入计数电路产生光栅线计数脉冲，送入ARMTDMI的中断计数程序中完成计数，最后将插值细分后的数据对中断计数校正完成编码输出到PCI总线上。

对于输送到计算机PCI总线上的4个读数头的数据，采用VC++6.0的多线程技术，为每一个读数头创建一个数据采集线程，以保证数据采集的实时性要求，同时在另一线程中对数据进行处理。

对采集到的读数头1、3的数据进行对径相加处理，形成数据A，同样对采集到的读数头2、4的数据进行对径相加处理，形成数据 B，再对 A、B两组数据进行对径相加处理，形成最后的数据用灯排显示，并将结果计算为度分秒显示在软件界面中。其实验系统如图8所示。

图8 实验系统Fig.8 Experimental system

3.2 检测结果

编码器的精度检测采用光管和23面棱体组合检测法，如图9所示。

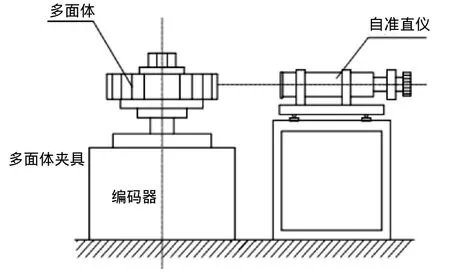
图9 精度检测原理图Fig.9 Schematic diagram of measure angle precision

将 DLT-23型多面体棱镜安放在编码器的回转中心上，其一个反射面的法线应与编码器的零位大致重合，然后将自准直仪对准这一反射面，用微动装置调到零位转换点，从自准直仪的数显箱读取一个数，然后继续转动编码器至第二个检测点，读取第二个数。以此类推，读取23个面的数据，它们与理论值的差，就是编码器的测角误差。误差曲线如图10所示。

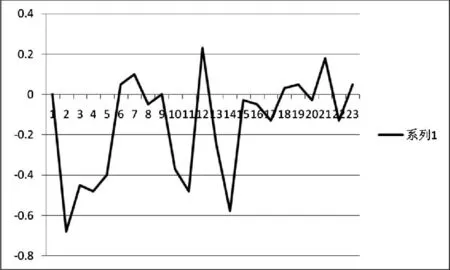
图10 误差曲线Fig.10 Curve of error

4 结论

对于28800线的主光栅，分100个区，上电后码盘输出绝对位置信息需要转过的最小寻零角度为：0.575°，角度测量分辨力约为：0.005″，精度可达到0.26″。可以满足目前大型经纬仪的使用要求。

准绝对式距离码编码器的2码道的编码方案，兼顾了绝对式和增量式码盘的特点，既缩小了码盘的尺寸，又可快速输出绝对角度位置，而且通过改变主光栅的线对数，可以达到更大的测量范围，具有很好的工程应用前景。

码盘分区越多，即N值越大，移动扫描的距离越小。距离编码减小了码盘刻划区，同时码道的数目减少，光电器件数减少数倍，提高了编码器的可靠性。

［1］叶盛祥.光电位移精密测量技术［M］.四川科学技术出版社，2003.

［2］曹振夫.小型绝对式矩阵编码器［J］.光学机械，1985（5）：65-70.

［3］韩旭东.增量式光电轴角编码器精度的组合比较检定法［J］.光学精密工程，2001（6）：80-84.

［4］熊经武，万秋华.23位绝对式光电轴角编码器［J］.光学机械，1990（2）：52-60.

［5］吴凡，刘恩海，方玉廷.GBJ128高精度绝对式光电轴角编码器［J］.光电工程，2000，27（6）：62-65.

［6］杨进堂，杨庆辉.莫尔条纹动态细分误差的测量［J］.计量学报，1998（7）：14-16.

［7］赵志巍.一种绝对式三轴联动多圈编码器的研制［J］.长春理工大学学报，2009，32（1）：8-10.