隧道开挖对周围土体及桩基影响的试验研究
孙 庆,杨 敏,冉 侠,Leung C F
(1.同济大学岩土及地下工程教育部重点实验室,上海200092;2.同济大学地下建筑与工程系,上海200092; 3.中信泰富(中国投资)有限公司,上海200080;4.新加坡国立大学土木工程系,新加坡119260)
由于城市大规模建设导致可用土地面积逐渐减少以及城市人口的不断增加,很多城市开始大规模开发地下空间,尤其是地铁建设更是如火如荼.但是在规划建设地铁隧道之前已经建成了很多建筑物,因此隧道开挖不可避免地要靠近已存在的桩基础.在软土中隧道开挖一般会引起明显的地表沉降,目前计算隧道开挖引起的土体自由场位移的方法主要有 Peck等[1]、M air等[2]提出的经验方法以及Loganathan等[3]提出的解析解.隧道开挖引起的土体位移会进一步引起邻近既有桩基内力和变形的变化,Hegarden[4],Loganathan[5],Feng[6],Jacobsz[7], Ong[8]等通过离心机试验模拟了隧道开挖对邻近桩基的影响.
本文主要是利用离心机试验对于隧道与桩的间距不同的情况下研究了隧道开挖引起的地表瞬时和长期沉降以及邻近桩基础的瞬时和长期反应,包括对桩基的竖向(轴力和沉降)和水平向(弯矩和侧向变形)的影响.
1 离心机试验模型
图1和图2分别给出了本文研究的离心机模型示意图和实物照片.本次试验是笔者在新加坡国立大学岩土工程实验室土工离心机上完成的.离心模型试验中的各项参数应与原型有一定的相似关系,才能保证模型反映原型的性状.基于量纲分析和控制方程,可以确定模型和原型的相似关系,离心机模型与原型之间常用物理量的相似准则可参考文献[9].试验过程中离心机稳定运转时加速度为100g.试验中所用模型箱由不锈钢合金制成,其内部尺寸为525 mm×200mm×490 mm(长×宽×高).模型箱的其中一面边墙为75mm厚透明的有机玻璃板,可以使安装在平台上的CV-M 1照相机获取试验中的图像.另一面边墙的中下部接通一个可以使丙酮溶液流入到隧道模型的管子.为了最小化土体与模型箱间的摩擦,模型箱的所有内墙都涂上一层润滑剂.模型箱内放置试验用的高岭土、隧道和桩模型以及测量仪器.本次试验所用的土为马来西亚高岭土(土颗粒相对密度Gs=2.65,液限wL=80%,塑限w P=40%,压缩指数C c=0.65,回弹指数C s=0.14).模型箱底部铺有20mm厚的砂层用来模拟底部的排水条件,砂层与粘土层由一薄层土工织物隔开,砂土的平均粒径为0.16mm,颗粒相对密度G s为2.65.

图1 离心机模型示意图(单位:mm)Fig.1 Sk etch of a typica l centrifugem odel pack age(unit:mm)

图2 离心机模型照片Fig.2 Photograph of a typical centrifugem odel package
1.1 模型桩
试验中的两根模型桩都是外边长为8.0mm,内边长为6.0 mm的方形铝管.桩长都是250.0 mm,并且沿桩身有10组应变片用以测量桩的轴力和弯矩.图3给出了模型桩的示意图.为了防止水和泥土引起应变片短路而无法正常工作,两根桩外均涂有一层环氧树脂保护.桩横截面的最终边长为12.6 mm,因此所模拟的原型桩的横截面边长为1.26 m.在试验之前,需要通过按悬臂梁方法对弯矩的测量进行多工况标定,以及通过在桩顶分级加载的方法对轴力的测量进行标定,荷载和输出应变之间的关系已由文献[6]详细阐述.
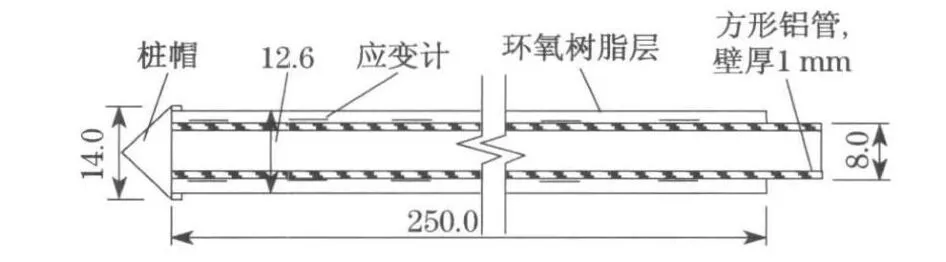
图3 模型桩示意图(单位:mm)Fig.3 Sketch o f instrumented model pile(unit:mm)
1.2 模型隧道
本文试验中所采用的模拟隧道开挖的方法是由Sharma等[10]在离心机试验中采用并改进的方法.图4和图5分别给出了模型隧道的示意图和实物照片.模型隧道的内部是高密度的聚苯乙烯泡沫,隧道衬砌由铜箔制成,把矩形的铜箔包在直径60mm的聚苯乙烯泡沫圆柱体外,连接处用电子焊枪进行焊接.模型隧道的长度为200mm,与模型箱的宽度一样.在100g的时候,相当于模拟一个直径6 m,长20m的隧道开挖.在模型隧道的内部要插入两根管子,分别用来提供和排出丙酮溶液.两根管子被绑在一起,以便在隧道开挖过程中可以迅速的排出液体.为了实现从上到下的隧道开挖顺序,两根管子置于模型隧道的拱顶附近.

图4 模型隧道示意图(单位:mm)Fig.4 Sketch of model tunnel(unit:mm)
1.3 试验过程
在进行离心机试验之前首先要进行土样的制备.将高岭土干粉末与水按质量比1∶1.2的比例在真空搅拌机内搅拌4~5 h直至浆液没有泡沫为止.然后将土样灌入到模型箱中达到预定高度,并使土样在20 kPa的压力下预固结一周左右,以缩短后续在离心机100g超重力场条件下的固结时间.

图5 模型隧道照片Fig.5 Photograph ofm odel tunnel
预固结阶段结束之后,土样中插入6个竖向位移传感器和4个孔压传感器,然后将模型箱放到离心机上加速到100g,使土体继续固结.在100g的重力加速度下持续4 h左右直到地表沉降和孔压稳定时,离心机停止转动进入下一阶段.
土体完成自重固结之后,离心机停止转动.把模型箱的前后挡板取下,将一直径为60mm,壁厚0.8 mm的不锈钢管在距土体表面150 mm处开挖一圆柱洞腔,与此同时将模型隧道插入洞腔中,然后将标记珠置于土中如图2所示位置,用来表征土体的运动轨迹,再将模型箱的挡板安装回原位.
模型箱安装固定好之后,使土体在100g的重力加速度下再次固结4 h左右,直至孔隙水压力和地表沉降读数稳定.然后打开电磁阀让丙酮流入模型隧道,隧道的开挖过程可以通过摄像机在控制室中进行观察,当隧道模型内的聚苯乙烯溶解之后,只剩下用来模拟隧道衬砌的黄铜箔来支撑土体.通过监测计算本次试验地层损失比为2%.为了进一步研究隧道开挖对土体位移以及桩基的长期影响,在开挖完成之后,离心机保持100g的重力加速度继续旋转直至孔隙水压力完全消散.试验过程中,孔隙水压力可由安装在土体中的4个孔隙水压力传感器(PPT)测得,安装在地表的传感器可以测得地表沉降曲线,而桩的变形和受力则由安装在桩上的激光传感器和应变计测得.
2 试验结果分析
除非特殊说明,以下试验结果均用原型尺寸进行说明.本文研究的3组试验简图如图6所示.在所有的试验中隧道的覆盖层厚度(C)和隧道直径(D)分别为12m和6m.试验1主要研究地层损失比为2%时隧道开挖引起的土体自由场位移和邻近桩基的反应.试验1,2,3对比研究隧道与桩的间距变化时,隧道开挖对桩基受力和变形性状的影响.试验1, 2,3中的隧道轴线与桩轴线之间的距离X分别为1.0D,1.5D,2.0D,即6,9,12 m.隧道开挖的地层损失比都是2%.

图6 试验简图Fig.6 Test sketch
本文将隧道刚刚开挖完成的阶段称为“瞬时”阶段,土体完全固结后的阶段称为“长期”阶段.通过试验发现隧道开挖720 d之后的土体位移和桩基反应基本可以忽略.
2.1 衬砌变形
图7给出了隧道衬砌的瞬时和长期变形形状.从图中可以观察到隧道衬砌的变形类似于椭圆,隧道衬砌在水平轴线方向是向两侧突出的,衬砌顶部是向下收缩的,底部变形很小.图中分别给出了隧道开挖2 d和720 d之后的衬砌变形情况,720 d之后衬砌的变形基本稳定.

图7 隧道衬砌随时间的变形示意图Fig.7 Sk etch of tunnel lin ing ovalisation w ith tim e
2.2 隧道开挖引起的土体位移
Peck等学者根据大量的实测资料提出用高斯曲线描述隧道开挖引起的地表沉降槽,地表沉降S的计算公式为
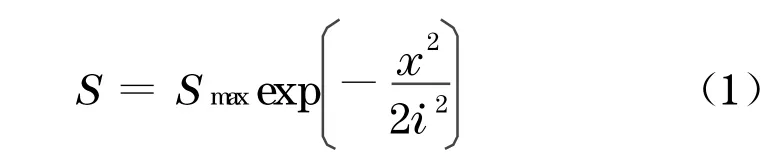
式中:x为从沉降曲线中心到所计算点的距离;S max为地面沉降的最大值,位于沉降曲线的对称中心上(对应于隧洞轴线位置),可由下式确定:

式中:V L为地层损失比,即单位长度地表沉降槽的体积占隧道开挖的名义面积的百分比;i为从沉降曲线对称中心到曲线拐点的距离,一般称为“沉降槽宽度”.根据O'Reilly和New的建议[11],i和隧道深度z0之间存在如下的关系:

式中:K称为沉降槽宽度系数,主要取决于土性.根据Mair等的建议对于粘土K取0.5是合适的.
图8所示经验公式计算得出的瞬时地表沉降曲线与离心机试验结果非常一致,且最大沉降值都出现在隧道中心线的正上方.从图8中可以看出,地表沉降随时间继续增大,这是粘土固结、土中孔隙水压力消散的结果,但到720 d之后地表沉降基本稳定.试验中地表沉降稳定的最大值为142 mm,比隧道刚开挖之后沉降的最大值31 mm增加了3.5倍,所以隧道开挖对地表沉降的长期影响是不容忽视的.经验公式得到的地表长期沉降最大值与试验值接近,但是沉降槽宽度要小于试验值,也就是低估了地表沉降的影响范围.

图8 地表沉降曲线的对比分析Fig.8 Comparison of surface settlem ent troughs
2.3 隧道开挖引起的桩基反应
隧道开挖对桩基的竖向和水平向受力性状都有影响,竖向影响包括桩的轴力和沉降,水平向的影响包括桩的弯矩和侧向变形.这些影响都是桩基设计时没有考虑的附加荷载,对桩基会产生附加沉降、轴力和弯矩.
2.3.1 隧道开挖引起的桩身轴力和沉降
由于试验中“轴向桩”的应变片在测长期效果时已经脱落,所以没有得到长期的试验结果.图9给出了试验1,2,3中隧道开挖完成瞬时引起的桩身轴力.轴力值都是从桩顶逐渐增加,在隧道起拱线深度(-15m)附近达到最大值,然后逐渐减小直至桩端.这说明对于长桩不论隧道与桩的间距如何变化,桩身竖向荷载的传递规律都是相似的.而且桩身轴力值随着隧道与桩间距的减小而增加.桩身最大轴力值由221 kN(隧道与桩间距为1.0D时)减小到129 kN(隧道与桩间距为1.5D时),最后当隧道与桩间距为2.0D时减小到82 kN.

图9 隧道开挖完成瞬时引起的桩身轴力Fig.9 Tunnelling-induced pile axial force p rofiles for short term

图10 隧道开挖完成瞬时桩基位置处自由场的土体沉降Fig.10 Free-field vertical soilmovem ent at pile location for short term
图10给出了隧道开挖完成瞬时桩基沉降以及在桩基位置处自由场的土体沉降.土体沉降随着与隧道间距的增加而减小,这与3组试验中轴力的变化规律相一致.这里引入一个新的概念——“中性面”.在中性面以上土体的位移大于桩的沉降,沿桩身产生的是负摩阻力,而在中性面以下桩的沉降大于土体的位移,沿桩身产生的是正摩阻力,所以桩身轴力在中性面处出现拐点达到最大值,这与图8所示桩身轴力的分布相吻合.而且不管隧道与桩的间距如何变化,中性面都位于隧道起拱线附近,这与桩的最大轴力位置相一致.
2.3.2 隧道开挖引起的桩身弯矩和侧向变形
隧道开挖引起的土体位移会引起邻近桩基的附加弯矩.图11给出了隧道开挖完成瞬时(short term,ST)和长期(long term,LT)的桩基弯矩随隧道与桩间距的变化情况.从图中可知,无论是长期效应还是瞬时开挖完成的影响,桩身弯矩最大值都位于隧道起拱线深度(-15 m)附近.这与Cheng[12]的数值分析和Pang[13]的现场实测数据相一致.桩顶和桩底的弯矩都为零,这是由于桩头自由而桩底约束相当于铰接的缘故.对于隧道开挖完成瞬时和长期所引起的桩身最大弯矩都随隧道与桩间距的增加而减小,但是减小的幅度越来越小,例如隧道开挖完成瞬时引起的桩身弯矩绝对值从151 kN◦m(隧道与桩间距为1.0D时)减小到61 kN◦m(隧道与桩间距为1.5D时),最后减小到42 kN◦m(隧道与桩间距为2.0D时).而不论隧道与桩的间距如何变化,桩身的最大弯矩都随时间的增加而增大,例如试验1中隧道开挖2 d后桩身的最大弯矩为-151 kN◦m,而隧道开挖720 d后的弯矩值为-213 kN◦m,其绝对值增加了41%,这充分说明了隧道开挖对桩基影响的时效性.

图11 隧道开挖引起的桩身弯矩Fig.11 Tunnelling-induced pile bendingm om ent
桩的侧向变形主要与土体位移、桩的抗弯刚度以及桩土间的接触有关.图12给出了3组试验中隧道开挖引起的桩身侧向变形.试验中由于桩顶是自由的,所以桩身的最大侧向变形都出现在桩顶位置.对于隧道开挖完成瞬时和长期所引起的桩身最大侧向变形都随隧道与桩间距的增加而减小.而不论隧道与桩的间距如何变化,桩身的最大侧向变形都随时间的增加而增大,例如试验1中隧道开挖2 d后桩身的最大侧向变形为4.1 m,而隧道开挖720 d后的变形值为8.0m,其值增加了近1倍.

图12 隧道开挖引起的桩身侧向变形Fig.12 Tunnelling-induced pile lateral def lection
3 结 论
本文通过3组离心机试验分析了隧道开挖完成瞬时及长期引起的土体位移及对邻近单桩的影响,并对隧道与桩的间距变化对桩基受力和变形性状的影响进行了研究,由于试验中“轴向桩”的应变片在测长期效果时已经脱落,所以结论中有关隧道开挖的长期影响中都不包括对桩身轴力和沉降的影响结果.主要结论如下:
(1)隧道开挖引起的地表沉降随时间逐渐增大,但到隧道开挖720 d之后基本稳定.最终沉降量要比初始沉降量增加了3.5倍,所以隧道开挖对地表沉降的长期影响是不容忽视的.高斯曲线法计算的瞬时沉降与试验值比较吻合,但是计算的长期沉降低估了地表沉降的影响范围.
(2)不论是瞬时开挖完成还是长期影响,隧道开挖引起的桩身最大轴力和弯矩都出现在隧道起拱线附近,而且桩基反应都是随着隧道与桩间距的增加而减小.
(3)本文引入了中性面的概念,在中性面以上土体的位移大于桩的沉降,沿桩身产生的是负摩阻力,而在中性面以下桩的沉降大于土体的位移,沿桩身产生的是正摩阻力,所以桩身轴力在中性面处达到最大值,
(4)隧道开挖引起的桩身长期弯矩和侧向变形比隧道开挖完成瞬时引起的弯矩和侧向变形有显著增加,说明隧道开挖对桩基的长期影响不容忽视.
[1] Peck R B.Deep excavations and tunneling in soft ground[C]∥ State of the A rt Report.Proceedings of the 7th International Conference on Soil Mechanics and Foundation Engineering.Mexico City:[s.n.],1969:225-290.
[2] Mair R J,Taylor R N,Bracegirdle A.Subsu rface settlem ent p rofiles above tunnels in clays[J].Geotechnique,1993,43 (2):315.
[3] Loganathan N,Poulos H G.Analy tical prediction for tunneling-indu ced ground movemen t in clays[J].Jou rnal of Geotechnical and Geoenvironmen tal Engineering,1998,124 (9):846.
[4] H egarden H JA M,Van Der Poel T J,Van Der Schrier JS. Ground movem ents due to tunneling:influence on pile foundations[C]∥Proc In t Sym posium on Geotechnical Aspects of Underg round Constru ction in Soft Ground. Rotterdam:Balkema,1996:519-524.
[5] Loganathan N,Poulos,H G,Stew art D P.Cen trifuge m odel testing of tunneling induced ground and pile deformations[J]. Geotechnique,2000,50(3):283.
[6] Feng SH.Centrifuge modeling of tunnel-pile in teraction[D]. Singapo re:National University of Singapore,2003.
[7] Jacobsz S W,Bowers K H,Moss N A,et al.The effects of tunnelling on piled structures on the CTRL[C]∥5th International Symposium on Geotechnical Aspects of Underground Construction in Soft Ground.Amsterdam: Taylor&Francis,2005:15-17.
[8] Ong C W,Leung C F,Chow Y K.Ex perimental study of tunnel-soil-pile in teraction[C] ∥ Proc Underg round Singapore.Singapore:National University of Singapore,2007: 256-263.
[9] Leung C F,Lee F H,Tan T S.Principles and application of geotechnical centrifuge model testing[J].Jou rnal of Institution of Engineers Singapore,1991,31:39.
[10] Sharma JS,Bolton M D,Boyle R E.A new technique for simu lation of tunnel excavation in a centrifuge[J]. Geotechnical Testing Journal,2001,24(4):343.
[11] O'Reilly M P,New B M.Settlemen t above tunnels in the United Kingdom-their magnitude and prediction[C] ∥Proceedings of Tunneling'82.London:Institu tion of M ining and Metallurgy,1982:173-181.
[12] Cheng C Y.Finite element study of tunnel-soil-pile in teraction [D].Singapore:National University of Singapore,2003.
[13] Pang C H.The effects of tunnel constru ction on nearby piled foundation[D].Singapore:National University of Singapore,2006.

