用约化方法对可展期的企业债券定价

任学敏,刘红梅

(同济大学 数学系,上海200092)

,化为抛物型方程的基本形式为

随着金融市场的发展和完善,投资者对金融风险的承受力的增强,发行企业债券成为公司融资的重要渠道.企业债券的明显特性是具有信用风险.目前处理企业债券定价和信用风险主要有两种方法,结构化方法和约化方法.结构化方法是把公司债券看成是关于公司资产的欧式看跌期权,其敲定价格为债务额.最早由Merton等人[1]提出.为解决由Merton模型得到的公司违约概率过低问题,考虑到公司可在债券到期前破产,Black和Cox等人[2]提出了首次通过模型,即当公司资产值下降到事先约定的阈值(违约边界)时,债权人有权强制公司破产以保护债券持有人的利益.Longstaff和Schwartz[3]把首次通过模型推广到随机利率情形.为解决连续模型的在债券快到期时的违约概率几乎为零的问题, Zhou[4]引入了跳扩散模型.而约化方法则把公司违约看成是一个外在的过程,用Poisson过程来描述,即第一次发生跳时公司就违约.约化方法由Jarrow和 Turnbull[5],Jarrow,Lando和 Turnbull[6]以及Duffie和Singleton[7]等人最早采用.

本文考虑一种可展期的企业债券,即企业在发行债券时事先约定,企业有权在债券到期日 T视市场利率水平决定是否以发行时的收益率把企业债的到期日延长到T1(T1＞T).显然,在到期日T,如果市场利率上升,企业的重新融资的成本将提高,企业将会选择延展债券的到期日;反之,如果市场利率下降,企业的重新融资的成本将下降,企业将不会延展债券的到期日.从债券投资人角度看,这给了企业一个规避利率风险的权利,同时,由于是企业债券,在可能的延展期[T,T1]内,投资人还要承受企业可能破产的风险,因此,必须给投资人以补偿,即提高其收益率或等价地降低售价.

1 约化方法简介及偏微分方程推导

约化方法仅考虑违约时间,回收率通常是外在(exogenous)给定的.跳的强度λ可为常数、确定的函数或随机过程.由于λ为常数时模型简单,使用上比较容易并能得到解析解,所以本文中采用λ为常数,λ为随机过程的情形可参阅文献[5-7].

由于Poisson过程在时段[s,t]发生k次跳的概率为

记τ为第一次跳发生的时刻,则公司[0,T]时段的违约概率为

1.1 利率r为常数时企业零息票债券定价

对可能违约的企业零息票债券,P(t,T)为其在t时刻的价格,假定其回收率为R∈[0,1].

(1)面值回收情形:回收在T时刻,原定在到期日T投资人可得1元的,一旦违约,则只能在到期日得到R元,其现值为

这里E(◦)为数学期望.

如R=0,则

这等价于违约日拿相应的无风险零息票的R倍,即

(2)市价回收情形:投资人在违约日拿违约前有风险零息票价值的R倍,这时

式(6)中第二个等号成立是因为问题类似于面值回收中回收为零的情形.可把回收率R看成是概率,公司在[t,t+dt]以概率λ dt违约,其中又以概率R不造成损害,以概率1-R得到零回收,亦即相当于公司以(1-R)λ dt的概率破产并回收为零,所以,由式(4)可得结论.式(4)和式(6)是很有启发性的,即在面值零回收和市价回收时,企业债券的处理与国债类似,只是由于信用风险的原因,其贴现率分别用r +λ和r+(1-R)λ代替以补偿投资者.

1.2 利率是随机时企业零息票债券定价

由于影响企业债券价格的主要因素是信用风险和利率的变化,因此通常应假定利率是随机的.记P(r,t)和D(r,t)分别为有相同到期日的零息票企业债券和国债的价格,在风险中性鞅测度下,假定短期利率服从Vasicek模型[8]

式中:α,θ,σr为正常数;Wt为标准布朗运动.构造一个投资组合Π=P(r,t)-Δ D(r,t),Δ为国债的份数.在[t,t+dt]时段,企业以概率1-λ dt不破产,由Ito公式,组合的价值变化为

可得

如果采用市价回收,即Q=ε P,这里0≤ε≤1,则企业债券满足

可得

从而

2 模型和求解

2.1 基本假设

(1)公司发行了零息票公司债券,到期日为 T,同时公司有权在到期日T决定是否以发行时的名义收益率把到期日延展到T1.

(2)公司的违约强度λ是常数,违约时间记为τ.一旦公司发生违约,回收为违约前市价的ε份, 0≤ε≤1,即采用市价回收.

(3)公司是否延展债券的到期日由在到期日 T的市场情况决定,即公司再举债的所需名义收益率高于初始的名义收益率时,公司将延展债券的到期日.

(4)市场利率满足Vasicek模型,即

2.2 定价公式

记D(t,r)为与公司的债券有相同到期日的无风险零息票的价格,则其有仿射结构解[8]

其中

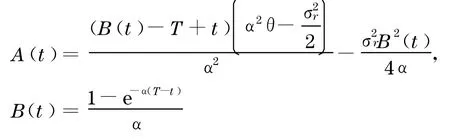
由式(13)和(15)可知,如果公司在T时刻发行在T1时刻到期的零息票公司债券,则其价格为

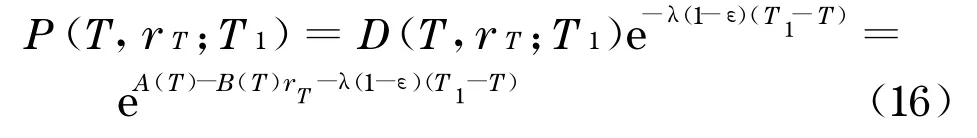
其中

由于在到期日投资人可得1元,其平均收益率RT,T1(连续复利)满足

从而

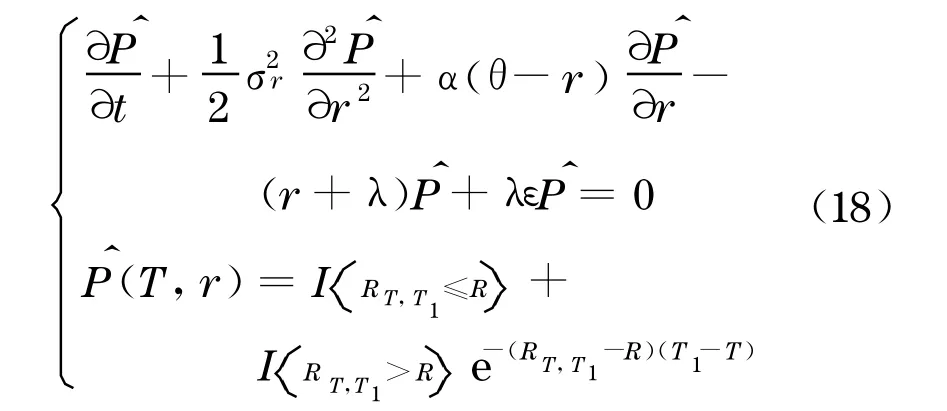
记τ=T-t,则方程可以改写为

其中

下面,用基本解的方法[9-10]求解方程(20),即设G(τ,r;ξ)为下面方程的解:

这里δ(◦)为δ函数.则问题(20)的解可以表示为

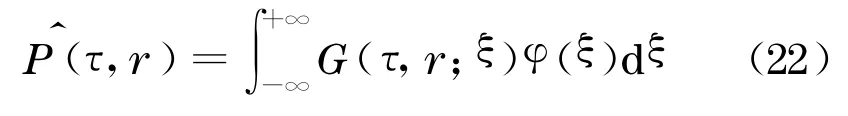
下面先求解问题(21),基本思路是化为标准型.

首先做函数变换G(τ,r;ξ)=ue-β(τ)r,以消去函数项系数中的r,则函数u满足下面的方程:

其中

再对问题(25)作函数变换u=Ve-ξ(τ)及自变量变换x=y+γ(τ),以消去函数和其一阶导数项,则V (τ,y)满足下面的问题:

,化为抛物型方程的基本形式为

由基本解的公式可得

将变换还原到原变量以及函数即得

其中β(τ),η,γ(τ)如前定义.故问题(20)的解为

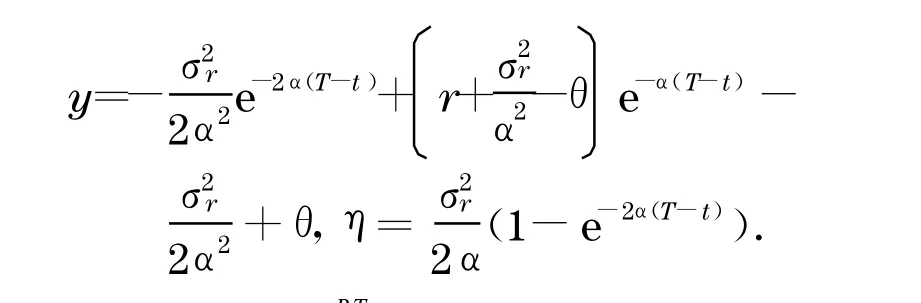
由R满足等式eRTP(0,r)=1,可得R为下面的超越方程的解:

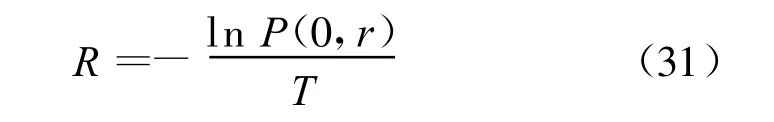
因为P(0,r)包含R.利用数值方法可求出名义收益率.

上述方法可进一步考虑公司信用等级的变化对债券价格的影响,利用标普或穆迪的信用等级转换概率矩阵可知在名义到期日时公司违约强度的改变的概率,只要在最后定价时取数学期望即可.

2.3 一些数值结果和分析

影响可展期企业债券名义收益率的因素有发行时的利率水平、到期日、可展期限、利率模型的参数、公司的违约概率和一旦违约时的回收率等,以下分析单个因素对可展期债券的收益率的影响.取参数α =0.379,r0=0.05,ε=0.4,σr=0.077,θ=0.098.

(1)在其他条件不变时,可展期债券的名义收益率比普通债券的收益率高以补偿投资者.

由图1可知,收益率差在可展期限固定时(3年),差额随到期日变大而减少,原因是补偿额分摊到了更长的时间段.其金融意义是显然的,理论证明也不复杂,因为可展期和普通债券满足的方程一样,但终值是普通债券的大,由极值原理即得结果.

(2)公司违约时回收越低或违约可能越大,可展期债券的名义收益率越高,以补偿投资人在可能的延展期内承受的更高的信用风险,但随着延展期变长,收益率曲线呈驼峰状,这与从普通企业债所得到的结果类似,实证研究也发现该结果.图2是在违约概率一定时,不同的回收率对债券收益率的影响.图3是在回收率一定时,不同的违约概率对债券收益率的影响.而图4是综合违约概率和回收率,即违约损失对收益率的影响.

(3)发行时的利率水平越高,可展期债券的收益率也越高,且随着可展期限的增加而增加,这是因为需给投资人的补偿增加(图5),但在可展期限一定时(3年),收益率并不一定随着债券到期日的增大而增加,这是由于补偿在更长期限的分摊和随着到期日变大,利率变化中的均值回归现象变得明显(图6).

图1 名义到期日与收益率差的关系Fig.1 Relationship betwee n the nominal maturity and diffrence of return rate s

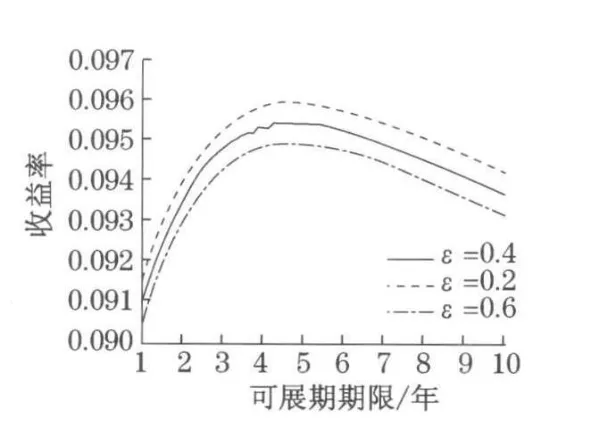
图2 回收率和可展期期限对收益率影响Fig.2 Impact of re cove ry rate and e xte ndable maturity on the return rate

图3 违约率和可展期期限对收益率影响Fig.3 Impact of default rate and extendable maturity on thereturn rate

图4 回收率和违约率及可展期期限对收益率综合影响Fig.4 T otal impact of recovery rate and default rate and e xte ndable maturity on the return rate

图5 初始利率水平和可展期期限对收益率的影响Fig.5 Impact of initial inte rest rate and exte ndable maturity on thereturn rate

图6 初始利率水平和首次到期日大小对收益率的影响Fig.6 Impact of initial inte rest rate and first maturity on thereturn rate

3 结论

从以上的讨论可知,可展期企业债券实际是一张嵌入利率期权并有违约风险的合约,相应的期权金和信用风险补偿体现在较高的回报率上.与一般的企业债券不同,其到期的名义回报(不违约时的回报)事先是不确定的,它依赖于将来的利率水平.补偿水平与利率未来的波动、可延展的期限及公司的违约可能的大小等因素有关.

[1] Merton R.On the pricing of corporate debt:the risk structure of interest rates[J].Journal of Finance,1974,29:449.

[2] Black F,Cox J C.Valuing corporate securities:some effects of bond indenture provisions[J].Journal of Finance,1976,31:351.

[3] Long staff F,Schwartz E.A simple approach to valuing risky fixed and floating rate debt[J].Journal of Finance,1995, 50:789.

[4] Zhou C.A jump-diffusion approach to modeling credit risk and valuing defaultable securities[R].Washing ton:Federal Reserve Board,1997.

[5] Jarrow R,TurnbullS.Pricing derivatives on financial securities subject to credit risk[J].Journal of Finance,1995, 50:53.

[6] Jarrow R,Lando D,Turnbull S.A Markov model for the term structure of credit risk spreads[J].Review ofFinancial Studies,1997,10:481.

[7] Duffie D,Singleton K J.M odeling term structure of defaultable bonds[J].Review of Financial Studies,1999,12:687.

[8] Vasicek O.An equilibrium characterization ofthe term structure[J].The Journal of Financial Economics,1977, 5:177.

[9] 姜礼尚.期权定价的数学模型和方法[M].北京:高等教育出版社,2003.

JIANG Lishang.The mathematical models and methods in option pricing[M].Beijing:Higher Education Press,2003.

[10] 姜礼尚,孙和生,陈志浩,等.偏微分方程选讲[M].北京:高等教育出版社,1997.

JIANG Lishang,SUN Hesheng,CHEN Zhihao,et al.Some topics on partial differential equation[M].Beijing:Higher Education Press,1997.