结构变形监测的单频GPS动态三差法

刘志平,何秀凤,张书毕,王 坚

(1.中国矿业大学 国土环境与灾害监测国家测绘局重点实验室,江苏徐州 221116; 2.河海大学卫星及空间信息应用研究所,江苏南京210098)

近年来,GPS技术在烟囱、高塔、桥梁等高耸和大跨度工程结构变形监测得到了应用并取得了较好效果[1-2],尤其是一机多天线技术为大范围精密变形监测实践的广泛开展提供了新思路[3].目前,GPS精密变形监测一般利用双差观测值提取变形,其关键难点是双差模糊度固定以及周跳探测与修复.为解决这些问题,陈永奇等提出了双频单历元模糊度快速固定方法[4].之后,张小红、李征航及徐绍铨等针对不同监测对象特点分别研究了改进单历元方法和似单差方法[5].但是,改进单历元法对初始值精度、观测视场和接收机硬件要求较高;似单差方法需对非差相位观测值进行钟差、大气误差等改正,而在无约束条件下采用单频单历元观测值固定双差模糊度的可靠性低[6].此外,以上提及方法均是先利用精确的初始值求解双差模糊度,为快速固定模糊度需经常更新初始值,同时要求监测对象的实际变形范围约半个波长,从而难以用于桥梁、高楼及烟囱等高耸和大跨度工程结构物的动态变形监测.

针对上述问题,本文提出了适合于高耸、大跨度结构等快速、大变形监测的单频GPS动态三差法.文中从函数模型、随机模型以及数学模型适用性分析三方面对该方法进行了详细阐述,其特点是三差值不存在模糊度参数,大气误差削弱更为彻底,基准点、基线向量分别采用伪距单点定位、单频相对定位即可满足动态三差模型的初始值精度要求,并可实时地估计动态三维变形.此外,对于三差值中的周跳影响,可采用抗差最小二乘法[7]处理,也利用时-频域转换方法[8-10]将其与结构信号进行分离.应用单频GPS动态三差法对南京长江三桥进行振动监测试验研究,计算结果显示,与双频单历元监测方法提取的变形序列基本吻合,且基于该方法求解的动态变形序列结合 Fourier频谱分析和经验模式分解EMD(empiricalmode decom position)准确地提取了三桥主梁一阶竖弯处的固有频率0.25 H z及其响应信号,表明新方法满足高精度动态变形监测的需要.

1 单频GPS动态三差法

1.1 函数模型

在图1所示的GPS动态三差法变形监测中,T1为基准点,T2,T2′分别为监测点初始位置与历元ti, ti+1变形后的位置,且T 1,T 2初始坐标和基线向量b已知,(ti)为某历元相应站点与卫星的距离,d为历元ti,ti+1的变形向量,δd为历元ti+1相对历元ti发生的动态变形.

图1 GPS动态三差法变形监测示意图Fig.1 Deformation monitoring w ith GPS dynam ic tr iple-differencem ethod

将式(3)减去式(2),并化为如下的函数关系式:

因此,若在某两连续历元基准站T 1与监测站T 2′同步观测n颗卫星,顾及式(4)右端第一项在动态变形监测应用中可忽略(见第1.3节),则基于式(4)～(5)可建立误差方程式如下:

式中:

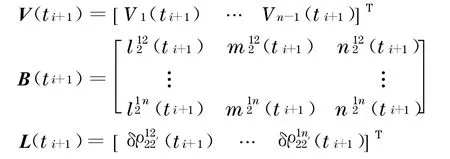
由函数模型(6)可知,该模型采用两个连续跟踪历元的单频三差值避免了模糊度固定难题,可实时估计动态变形δd.而且,模型参数δd不会如单历元模型参数d的求解受限于模糊度固定问题,没有“约半个波长”的上限约束.此外,模型中设计矩阵B不同于常规静态三差模型设计矩阵,而与双差模型中基线参数的系数矩阵完全一致,建模极为方便.因此,称函数模型(6)为适于快速、大变形监测的单频GPS动态三差模型,相应的数据处理方法称为单频GPS动态三差法.

1.2 随机模型

大量的理论和实践研究表明,基于卫星高度角的正弦函数定权方案可较好地表示GPS观测值的先验方差.若某观测历元ti同步观测卫星数为n,则可将基准站T1、测站T2′至各卫星的非差相位观测值先验方差定义为

式中:一般取a=3 mm,b=5mm[5];E为相应站点的卫星高度角.

设不同卫星、测站之间的相位观测值不相关,则利用误差传播定律可得某观测历元ti双差相位观测值的方差协方差矩阵为(s1为参考卫星)

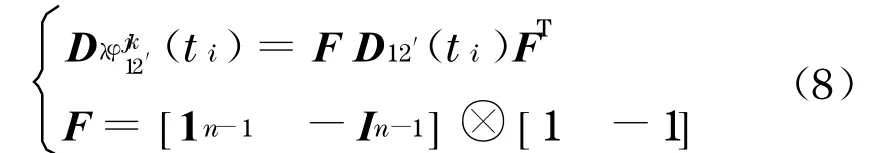
式中:⊗为K ronecker积;1n-1表示n-1维元素均为1的列向量;I n-1为n-1阶单位矩阵.

进一步假设历元间的双差相位观测值不相关,则基于式(8)可得动态三差法随机模型为

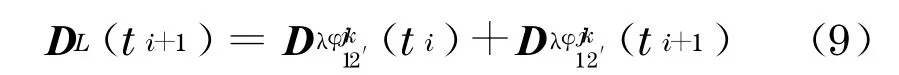
1.3 适用性分析

1.3.1 对初始值精度的要求

式中:mx1表示基准点的误差列向量;mb表示基线向量的误差列向量.

1.3.2 对双历元时间间隔的要求

基于式(4)和(6),在动态变形监测条件下忽略参数d,则与式(10),(11)同理可得动态三差模型误差σM满足下式:

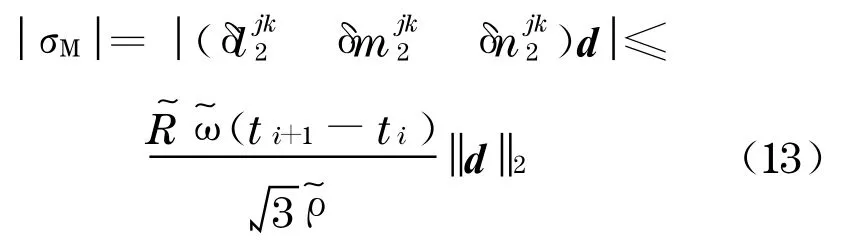
1.3.3 对共视卫星数的要求

在动态变形监测情况下仅考虑参数δd,综合函数模型(6)和随机模型(9)可得动态变形的最小二乘参数估计为

由式(15)可知,单频载波同步观测卫星4颗以上便可估计动态三差模型参数,对于双基准-动态三差模型,共视卫星数可降低为3颗.

1.3.4 载波相位周跳的影响分析

若某观测历元发生周跳,则利用该历元及其相邻历元观测值的动态变形进行求解将受影响.但对于三差观测值,载波相位周跳相当于粗差,只需采用抗差最小二乘法即可得到正确的动态变形[7],而不必进行周跳探测与修复.而且,在桥梁、高楼以及工业烟囱等大跨度和高耸的工程结构物动态变形监测实践中,由于对空观测视场开阔、信号信噪比高,长时间连续周跳的概率低.此时直接由式(15)获取整个连续监测时段内的三维动态变形序列,则该序列在频率域上表现为周跳发生的频率特征与振动监测信号频率特征的叠加.对此序列进一步分析可知,时序中振动信号的主频特性会贯穿整个时域,而周跳频率特性随环境变化不会固定不变地贯穿整个时域,在频域内表现出不同信号的频谱差异.因此,也可在后处理过程中采用时频分析工具分离周跳的影响[8].

2 结构监测试验与结果分析

大型桥梁是在工程测量中较为常见的结构监测对象.为验证GPS动态三差法的正确性和有效性,将该方法应用于南京长江三桥结构振动监测试验研究.南京长江三桥全长约15.6 km,其中跨江大桥长4 744m,主桥跨径648 m.三桥振动监测试验采用三台接收机,其中两台分别设在主桥南侧和桥中心布索区作为监测点,另一台设在南岸防洪堤坝带有强制归心装置的观测墩上作为基准点.数据采集于2008年5月19日10时,分3个时段进行,卫星截止高度角设为10°,各采样时段长度约为2 h,采样频率分别设置为2,5和10H z.现采用动态三差法对桥中心测点5 H z时段L1载波观测值按0.2 s时间间隔逐历元解算动态变形.图2显示了高程方向的动态变形计算结果(5 000个历元).

图2 桥中心点高程动态变形时序及频谱分析Fig.2 Vertical dynam ic deformation and Fourier spectrum o f the bridge cen ter

图2a曲线表示三桥在车辆负荷、风力效应等条件下的高程方向变形序列,其中也包含了GPS相位观测值各种误差影响.为分析该动态变形序列的频率特征,对该序列直接进行Fourier频谱分析,如图2b所示.由图2b频谱分析结果可知,三桥中心点(主梁一阶竖弯)垂直变形序列的主频约为0.25Hz,与有限元计算的固有频率0.245 3 H z[11]基本一致.

图3表示动态三差法和单历元法获取的单历元变形及其较差.图3a单历元变形由图2a动态变形序列进行一阶累加生成,图3b采用双频单历元方法解算并将后续变形减去第1个历元的变形而得,图3c表示以上两种方法所得的单历元变形差值.图3a正变形最大值为36.5 mm、负变形最大为-61.2 mm,分别对应第335,1 979个历元,图3b中相应历元的变形为29.3 mm、-63.4 mm;图3b正变形最大值为32.9 mm、负变形最大为-64.1 mm,分别对应第1 072,1 980个历元,图3a中相应历元的变形为30.2 mm、-56.9 mm,结果均比较吻合.图3c中,变形较差均值为-1.2 mm,均方根值为4.9 mm,且基本服从正态分布,与当前GPS载波观测精度水平一致.因此,在图2结论的基础上,图3进一步验证了文中GPS动态三差法的正确性和有效性.应说明的是,时段内可见卫星达9～10颗,为双频单历元方法确定三维变形和模糊度参数提供了良好数据条件,而文中动态三差法采用单频载波即可快速估计动态变形,且避免了模糊度固定的难题.

图3 动态三差法与单历元法变形结果比较Fig.3 Comparison of deformation by single-epoch method and dynam ic trip le-dif ferencemethod

为从动态变形中识别和提取三桥固有模态响应信号,利用经验模式分解(EMD)法[10,12]和Fourier频谱分析对动态变形序列进行分解与频谱分析.为节省篇幅,仅显示了部分EMD分量及其频谱,见图4.比较图4b中EMD分量im f4与图2b频谱可知,模态函数分量im f4与动态三差法变形时序的主频一致,表明图4a中EMD分量im f4即为南京三桥中心点结构固有模态的响应信号.此外,现有研究表明多路径效应周期一般在数十秒至数十分钟之间,初步判断EMD残余res包含了多路径效应等误差.

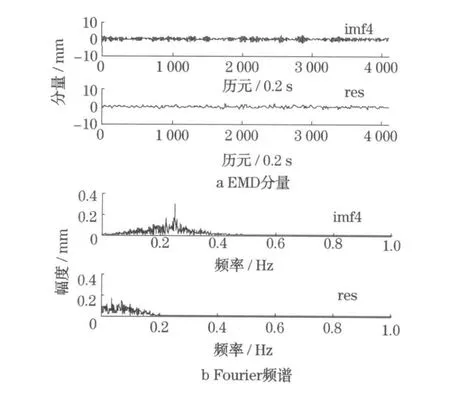
图4 高程动态变形EMD分量及其Fourier频谱Fig.4 EMD com ponen ts and its Four ier spectrum of vertica l dynam ic deform ation

3 结论

本文提出了适用于工程结构快速、大变形监测的单频GPS动态三差法.该方法利用采样率约0.1 Hz以上动态数据,仅考虑动态变形参数,摒弃了单历元法和似单差法需正确固定模糊度的关键难题,具有初始值精度要求低和实际动态变形无半个波长上限约束的特点.结合南京长江三桥结构振动监测试验对所提出方法进行验证,结果表明,单频动态三差法与双频单历元方法所获单历元高程变形量在5 mm均方误差意义下一致,且基于该方法得到的动态变形序列采用经验模式分解和频谱分析正确提取了三桥主梁一阶竖弯处的固有频率为0.25 H z及其响应信号.此外,鉴于文中短基线、高采样率的应用情况,未考虑电离层误差模型改正.随着GPS现代化和GALILEO计划的完成,若将单频动态三差法推广至双频、多频动态三差法,可进一步提高动态三差法结构变形监测的精度及可靠性.

[1] Li Xiaojing,Ge Linlin,E liathamby Ambikairajah,et al.Fu llscale structu ral monitoring using an in tegrated GPS and accelerom eter sy stem[J].GPS Solu tions,2006,10:233.

[2] Clem en t Ogaja,Li Xiaojing,Chris Rizos.Advances in structu ral monitoring with global positioning system technology:1997—2006[J].Journal of Applied Geodesy, 2007,1(3):171.

[3] HE X F,YANG G,DING X L,et al.Application and evaluation of a GPSmulti-an tenna system for dam deformation monitoring[J].Earth,Planetsand Space,2004,56(12):1035.

[4] 陈永奇,James Lutes.单历元GPS变形监测数据处理方法的研究[J].武汉测绘科技大学学报,1998,23(4):324.

Chen Yongqi,James Lu tes.Developm ent of the methodology for single epoch GPS deformation m onitoring[J].Jou rnal of Wuhan Technical University of Surveying and Map ping,1998, 23(4):324.

[5] 刘志平.基于GNSS精密定位方法的高边坡变形稳定性研究[D].南京:河海大学土木工程学院,2009.

LIU Zhiping.GNSS-based deformation m onitoring and stability analysis of steep slopes[D].Nan jing:H ohai University.College of Civil Engineering,2009.

[6] 胡丛玮,刘大杰.单历元确定GPS整周模糊度的分析[J].南京航空航天大学学报,2001,33(3):267.

HU Congw ei,LIU Dajie.Prelim inary analysis on single epoch GPS ambiguity resolution[J].Jou rnal ofNanjing University of Aeronau tics&Astronau tics,2001,33(3):267.

[7] Yang Y,Song L,Xu T.Robust estimator for correlated observations based on bifactor equivalent w eigh ts[J].Jou rnal of Geodesy,2002,76:353.

[8] H ristopulos D T,Mertikas S P,A rhontakis I,et al.Using GPS formonitoring tall-building response to w ind loading:filtering of ab rupt changes and low-frequency noise,variography and spectral analysis of displacem ents[J].GPS Solutions,2007, 11:85.

[9] 姚连璧,姚平,王人鹏,等.南浦大桥形变GPS动态监测试验及结果分析[J].同济大学 学报:自然科学版,2008,36 (12):1633.

YAO Lianbi,YAO Ping,WANG Renpeng,et al.GPS-based dynam icmonitoring and analy sis of Nanpu Bridge deformation [J].Journal of Tongji University:Natu ral Science,2008,36 (12):1633.

[10] 刘超,王坚,胡洪,等.动态变形监测多路径实时修正模型研究[J].武汉大学学报:信息科学版,2010,35(4):481.

LIU Chao,WANG Jian,HU Hong,et al.Research on realtime correcting model of multipath in GPS dynam ic deformation monitoring[J].Geomatics and Information Science ofWuhan University,2010,35(4):481.

[11] 朱乐东,李超,郭震山.环境随机振动频域法全桥气弹模型模态识别[J].结构工程师,2005,21(6):38.

ZHU Ledong,LIChao,GUO Zhenshan.M odal identification of full bridge aeroelastic model with frequency-dom ain app roach of ambient random vibration[J].Stru ctural Engineers,2005, 21(6):38.

[12] Flandrin P,Riling G,Goncalves P.Empirical mode decomposition as a filter bank[J].IEEE,Signal Processing Letters,2004,11(2):112.