非接触爆炸下纵向箱型梁舰船的极限承载能力研究
王佳颖 张世联 彭大炜
上海交通大学船舶海洋与建筑工程学院,上海 200030
非接触爆炸下纵向箱型梁舰船的极限承载能力研究
王佳颖 张世联 彭大炜
上海交通大学船舶海洋与建筑工程学院,上海 200030
以德国F124护卫舰纵向箱型梁甲板结构型式的舱段为研究对象,采用流固耦合方法计算其在空爆作用下的甲板变形。采用阻尼因子法,对各冲击因子下箱型梁和普通甲板结构型式舱段塑性变形后的极限承载能力进行比较分析。研究结果表明:在遭受非接触爆炸冲击后,箱型梁甲板结构型式与普通甲板结构型式相比,具有变形小、变形后舰体极限承载能力下降低等优势,因而能够显著提高舰船生命力。
纵向箱型梁;极限承载能力;大变形损伤;非接触爆炸;阻尼因子法
1 引言
在实际作战中,水面舰船强力甲板会遭受各式武器(如反舰导弹、激光炸弹等)的打击。其中空中非接触爆炸冲击波由于其冲击范围较大,当炸药量较大时,会使船体强力甲板产生大变形破坏,而强力甲板的大变形会明显削弱舰船总纵极限承载能力,降低舰船生命力。
为提高舰船生命力,各海军强国积极研究开发新型防护结构形式。其中在舰船强力甲板上设置纵向箱型梁,已在欧洲一些新型作战舰船 (图1)上得到了实际运用[1]。目前,对于舰船受损后极限承载能力已经开展一些研究[2-7]。但与纵向箱型梁舰船受损后极限承载能力有关的公开研究资料不多。本文以德国F124护卫舰纵向箱型梁的3根箱型梁布置型式为参考研究对象,设计了普通舱段、新型纵向箱型梁舱段结构及其空中非接触爆炸工况,采用流固耦合方法计算两种舱段强力甲板塑性变形。采用SMITH法和非线性有限元阻尼因子法对两种舱段完整状态下极限承载能力进行计算比较,验证阻尼因子法的可靠性。然后通过阻尼因子法计算不同大小非接触爆炸冲击因子下舱段变形损伤下的极限承载能力。探讨了在非接触爆炸后纵向箱型梁舰船结构型式与常规结构型式相比其极限承载能力的优势。研究结果表明新型纵向箱型梁能够显著提高舰船生命力。
2 舱段结构与爆炸工况设计
取舰船平行中体三舱段为设计对象,首先设计了普通舱段结构(以下简称模型Ⅰ),并且以模型Ⅰ为母型,参照F124护卫舰在强力甲板上设置3根新型纵向箱型梁,即为纵向箱型梁舱段(以下简称模型Ⅱ)。箱型梁高宽均为0.8 m,板厚为10 mm。添加箱型梁后,横剖面面积增加约6%,中和轴提高约0.32 m,甲板剖面模数增加约16%。图2给出了纵向箱型梁舱段的横剖面示意图。
这里设计爆炸炸药中心距强力甲板中心上方6 m。炸药类型为标准TNT炸药,炸药量分别为300、450、600、800、1 000 kg。 这里用基于冲击波超压的冲击因子Φ来描述爆炸冲击的强弱,这种冲击因子的定义如下:

式中,Φ 为冲击因子;W 为炸药(TNT)重量,kg;R为爆心与目标点的距离。
表1对各工况炸药重量、冲击因子等进行了编号汇总。

表1 爆炸计算工况汇总表Tab.1 Summary of explosion calculation conditions
3 舰船舱段爆炸载荷下的塑性变形计算
3.1 爆炸冲击有限元计算方法
这里采用显示求解方法和流固耦合技术求解非接触爆炸问题,在空间域内采用拉格朗日和欧拉两种求解方法。为节省计算时间,舰船平行中体三舱段采用二维板单元模拟,其余船体部分使用一维梁单元模拟,其惯性距和质量匹配船体梁参数。船体振动过程中的附连水质量计算采用Lewis F M和Todd F H等人提出的计算公式和图谱分析的方法[8]来计算。采用0维弹簧单元模拟水弹性,梁单元与三舱段模型间采用刚性MPC连接。爆炸冲击波对舰船舱段的破坏作用采用能够考虑耦合面破裂的流固耦合算法,这需要快速耦合算法(Param,Fastcoup)[9]。
空气和炸药由欧拉单元来模拟,其中炸药采用高密度高能空气来模拟,建立两个欧拉域,分别为舱段外部空气介质和爆炸目标强力甲板下方封闭舱室空气介质。在计算中建立两个一般耦合关系[10],分别用来描述舱段外部空气与舱段外部的耦合以及爆炸目标强力甲板下方封闭空气与周围舱室板的耦合。计算初始时间步长取1×10-6s,最小步长1× 10-10s,计算时间为 0.08 s。 图 3 给出了舰船有限元总体模型图,图4给出了爆炸一般耦合关系示意图。
这两种方法在时间域上均采用显示积分法,以拉格朗日法为例对显示积分方法加以说明。如果当前时间步是步n,显示求解方法将运动微分方程:



假设加速度在一个时间步长上是恒定的,采用中心差分法进行时间推进:

这里采用空气欧拉域爆炸冲击波的计算用欧拉求解器,其采用控制容积法和显式积分做材料流动的具体方法如下。
将控制方程在流场中任意封闭曲面所包含的容积内进行积分,得到积分形式的控制方程:

对控制方程进行一系列变换得到关于单元型心处的各物理量在tn+1时刻的线性方程:


式中,FM为单元形心处的质量;FMom为单元形心处的动量;FTE为单元形心处的能量。在已知tn时刻的各物理参数已知的情况下,可以求出tn+1时刻的各物理参数。
3.2 材料本构关系与状态方程
EOSGAM模型定义空气的γ律状态方程:

式中,p 为压力;e 为比内能,取 0.21 GJ/m3;ρ为空气密度,取 1.25;γ 为比热比,取 1.4。
TNT炸药用高能密度空气模拟,密度为1 600 kg/m3,能量密度为 4.2 GJ/m3。
舱段结构采用双线性弹塑性应力应变关系,密度 7.85 ×103kg/m3,弹性模量 2.1 × 105MPa,泊松比0.3,静态屈服应力390 MPa,硬化模量2 154 MPa,失效应变0.18。材料采用能考虑动态应变率效应的Cowper-Symonds模型,同时考虑材料应变强化效应,其本构方程如下:

式中,σd为动态应力;σ0为初始屈服极限;σy为静态屈服应力;ε˙为等效应变率;材料常数 D = 40/s,P=5,E 为弹性模量;Eh为硬化模量;εp为等效塑性应变。
3.3 爆炸冲击波的传播
在外部空气欧拉域中炸药爆炸后所形成的冲击波快速地向外传播。此处以工况model I6,600为例,图5显示了不同时刻冲击波压力分布图,包括了冲击波初始压强分布图(0 ms)、冲击波传播图(2 ms)、冲击波与舰船结构的相互耦合(4 ms)以及冲击波的绕射作用图(8 ms),最终外部欧拉域会恢复至大气压强平衡状态。
3.4 强力甲板变形结果
从工程角度看,一般塑性动力学问题关心的是结构的最大变形。这里结构最大变形发生在炸药下方舱段两横舱壁之间的强力甲板,因此将其取出分析其变形结果。模型Ⅰ强力甲板的最大变形发生在甲板中心处,而模型Ⅱ强力甲板的最大变形点发生在甲板中心略偏处。图6a和图6b分别给出了模型Ⅰ和模型Ⅱ强力甲板中心点的垂向位移随时间变化曲线。图7a和图7b给出了工况modelⅠ6,1000和工况 modelⅡ6,1000的舱段变形图。

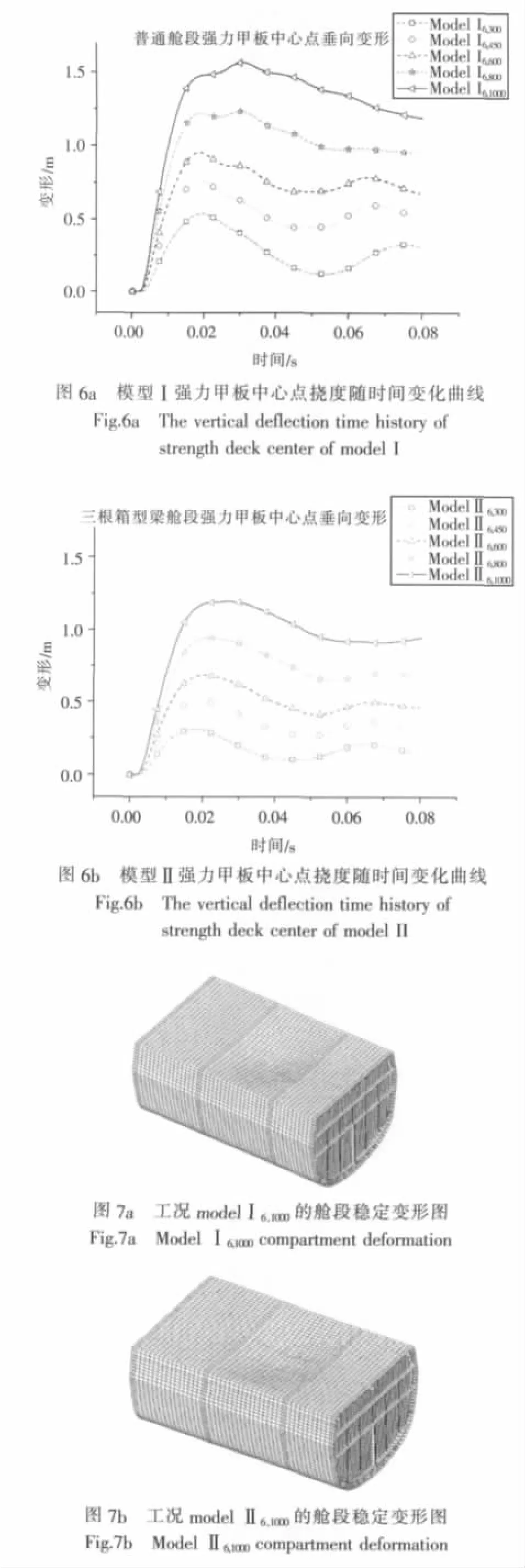
由计算结果可知,在相同的爆炸载荷作用下,模型Ⅱ的结构变形明显小于模型Ⅰ,且模型Ⅱ的大变形模式与模型Ⅰ相比,发生了明显的变化。普通强力甲板的大变形模式从舰体横剖面看呈半波型;而新型纵向箱型梁强力甲板的大变形模式从舰体横剖面看呈W型。不同的变形模式会改变强力甲板的极限轴向承载能力。
4 舱段极限承载能力的计算
4.1 极限承载能力计算方法
本文目的是研究纵向箱型梁对舰船舱段极限承载能力的贡献,因此这里主要考察舱段中垂极限承载能力。为简化计算,文中极限承载能力的计算忽略爆炸后结构残余应力影响,仅考虑塑性变形对舱段极限强度的影响。目前,常用的船体极限分析方法可分为:直接计算法、逐步破坏分析法(Smith法)、非线性有限元方法和理想结构单元法。文中采用法国船级社MARS 2000程序对船体极限承载能力进行Smith法计算,使用ABAQUS软件对非线性有限元法的舱段极限承载能力进行计算。
非线性有限元法常用的有三种求解方法:弧长法、阻尼因子法以及准静态法。由于阻尼因子法[11]比弧长法在数值收敛性上更好,比准静态法计算效率更高,因此文中采用阻尼因子法进行极限承载能力的计算。
阻尼因子法采用载荷步长增量来进行非线性迭代求解。其通过在平衡方程式中引入阻尼力项来求解结构不稳定崩溃的问题,求解的平衡方程为:

式中,{Fν}为阻尼力矢量,取决于结构变形的速度,其计算公式如下:

式中,c为阻尼系数;M*为人工质量矩阵;广义节点速度{ν}= {Δu}/Δt。
加载的初始阶段,结构处于稳定状态,此时广义节点速度{ν}很小,故阻尼力项{Fν}很小,可以忽略。随着载荷的不断增加,结构趋向于不稳定,当外载{P}已经不能完全由结构内力{I}来平衡时,结构达到极限状态,相当部分的应变能将释放转化为动能,广义节点速率{ν}迅速增大。此时,阻尼力项{Fν}通过做功消耗释放的应变能,从而在平衡方程式(14)中起到维持求解系统的“平衡”作用。
阻尼因子法无法继续有效跟踪结构在“卸载”过程中的载荷—位移路径,通过考察阻尼力项{Fν}为维持系统“平衡”所做功的历史变化曲线,就能够确定结构的极限承载能力。
为了能较精确地计算大变形损伤状态下舰体的极限承载能力,将平行中体3舱段变形后的有限元模型进行细网格划分。在舱段模型两端部建立刚性MPC,主节点在剖面型心处,从节点包括舱段端部所有节点,在两个主节点上施加相反方向、大小相等的弯矩,计算舱段极限承载能力。
由于Smith法目前还不能对变形受损下的舱段极限强度进行计算,因此本文首先采用法国船级社MARS 2000软件中Smith法和阻尼因子法对两种舱段完整状态下极限承载能力进行计算比较,考察非线性有限元阻尼因子法的可靠性,然后采用阻尼因子法对各爆炸因子下舱段受损后的极限承载能力进行计算。
4.2 完整状态极限承载能力计算
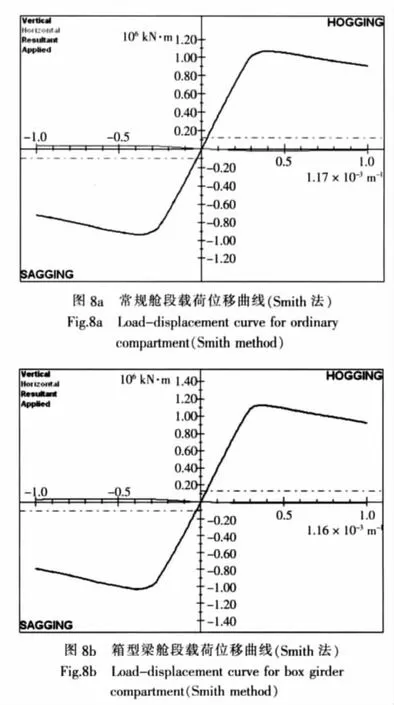
采用Smith法和阻尼因子法计算两种舱段完整状态下的极限承载能力。图8给出了Smith法计算得到的两种舱段完整状态下载荷位移曲线。图9给出了非线性有限元阻尼因子法计算得到的两种舱段完整状态下载荷位移曲线。当舱段结构达到了极限状态时,阻尼项所做的功骤然增大。图10给出了两种舱段完整状态下,使用阻尼因子法加载中阻尼项所做的功。
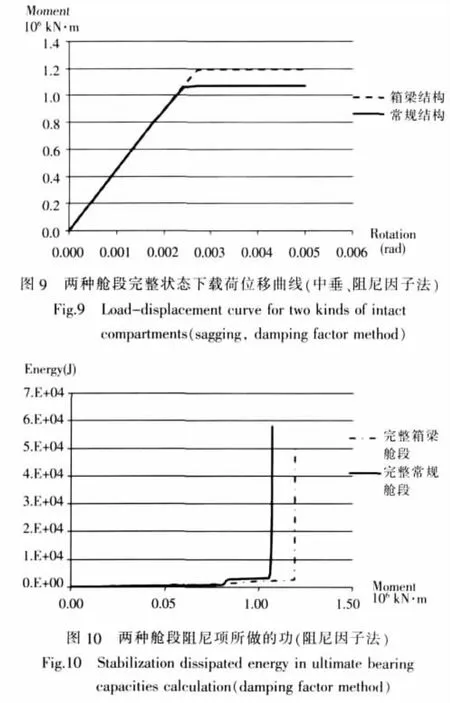
表2比较了采用Smith法和阻尼因子法对两种舱段完整状态下极限承载能力的计算结果。Smith法计算的极限承载能力要略小于阻尼因子法的计算结果,这是由于MARS 2000中考虑了板格的初始变形以及焊接残余应力等影响,而非线性有限元计算中并没有考虑这些不利因素。

表2 Smith法和阻尼因子法极限承载能力计算结果比较Tab.2 Comparison of ultimate bearing capacities between two calculation methods
4.3 受损后极限承载能力计算
图11a给出了 modelⅠ6,1000工况的舱段极限状态应力图;图11b给出了modelⅡ6,1000工况的舱段极限状态应力图。图12a给出了受损后普通舱段载荷位移曲线;图12b给出了受损后箱型梁舱段载荷位移曲线。

根据非线性有限元计算结果,普通舱段在大变形损伤状态下中垂极限崩溃过程如下:
1)由于强力甲板中心区域的变形过大,中心区域的承载能力很小,强力甲板靠近舷侧区域的结构面内应力不断增大,接近屈服状态;


2)屈服区域不断扩大,甲板整体变形开始增大;
3)强力甲板和舷侧等纵向结构都呈现极限状态,船体梁的承载能力无法再提高;
4)随着强力甲板纵桁的弯压崩溃,强力甲板整体失去轴向承载能力,发生卸载。
纵向箱型梁舱段在大变形损伤状态下中垂极限崩溃过程如下:
1)强力甲板中间纵向箱型梁受压接近屈服状态;
2)强力甲板靠近舷侧区域的结构面内压应力增大,屈服区域不断扩大,甲板整变形开始加大;
3)强力甲板和舷侧等纵向结构都呈现极限状态,船体梁的承载能力无法再提高;
4)随着强力甲板纵桁与纵向箱型梁的崩溃,强力甲板整体失去轴向承载能力,发生卸载。
表3给出了完好状态和不同非接触爆炸冲击因子下大变形损伤状态后,模型Ⅰ和模型Ⅱ舱段的各工况中垂极限强度计算值和对应的最大变形,与完好状态相比大变形损伤状态极限承载能力的降低比例,以及模型Ⅱ与模型Ⅰ各工况极限承载能力之比。图13给出了两种舱段极限承载能力随非接触爆炸冲击因子变化曲线。

表3 大变形损伤状态下中垂极限承载能力对比Tab.3 Ultimate strength comparison of the two kinds of compartments under large deformation damage condition

分析计算结果,可以得到如下结论:
1)在完整状态下,纵向箱型梁使中垂极限强度提高了 11.9%;
2)在相同的非接触爆炸冲击载荷作用下,新型箱型梁舱段强力甲板的最大变形比普通舱段的减小21%以上;
3)随着冲击因子的增加,变形后的新型箱型梁舱段极限承载能力的下降速度要明显低于普通舱段;
4)设置3根新型箱型梁强力甲板在非接触爆炸载荷变形后变形模式接近W型,在相同爆炸载荷冲击下,中间箱型梁能减小板架整体变形,增加了塑性变形后强力甲板的有效承载宽度和承载能力,因此新型箱型梁舱段在非接触爆炸冲击下较普通舱段具有更高的承载能力。
5 结论
1)本文以德国F124型护卫舰为研究对象,通过对不同冲击因子下的普通舱段和新型箱型梁强力甲板变形后的极限承载能力进行非线性有限元计算,研究结果证明,新型纵向箱型梁舰船在遭受非接触爆炸冲击后,与普通舰船相比,具有强力甲板变形模式更优、变形更小、船体极限承载能力损失小等优点,能够显著提高舰船生命力。
2)非接触爆炸冲击后造成的材料残余应力应变、热应力等其他因素也会对爆炸冲击后船体极限承载能力带来一定程度的影响,其机理较为复杂,还需在今后研究中进一步分析。
[1]王正国,熊治国.决定舰船生命力的因素[J].国外舰船工程,2005(12):1-6.
[2]马春燕.水面舰艇新型抗损结构设计与剩余强度研究[D].哈尔滨:哈尔滨工程大学,2006.
[3]杨平,刘俊梅.破损船体剩余极限强度的评估与分析[J].武汉理工大学学报,2006,30(6):1034-1037.
[4]聂武,冯琦,陈国龙.舰艇破损剩余强度反分析研究[J].哈尔滨工程大学学报,2003,24(5):473-476.
[5]祁恩荣,崔维成.破损船体极限强度非线性有限元分析[J].船舶力学,2005,9(5):83-91.
[6]AKHRAS G,GIBSON S,YANG S.Ultimate strength of a box girder simulating the hull of a ship[J].Canadian Journal of Civil Engineering, 1998,25(5):829-843.
[7]刘玉秋.大型水面舰船主船体破损后应力及剩余强度研究[D].哈尔滨:哈尔滨工程大学,2001.
[8]金咸定,赵德有.船体振动学[M].上海:上海交通大学出版社,1997.
[9]丁沛然,钱纯.非线性瞬态动力学分析—MSC.DYTRAN理论及应用[M].北京:科学出版社,2006.
[10] MSC.MSC/DYTRAN Version 4.0 User’s Manual [M].U.S.A.,1997.
[11] ABAQUS.ABAQUS Analysis User’s Manual[M].U.S.A.,2007.
Ultimate Bearing Capacity Analysis of Longitudinal Box Girder of Warship under Non-contact Explosion
Wang Jia-ying Zhang Shi-lian Peng Da-wei
School of Naval Architecture,Ocean and Civil Engineering,Shanghai Jiaotong University,Shanghai 200030,China
Utilizing the longitudinal box girder deck structure of Germany F124 frigate as a study case,the strength deck deformations under non-contact explosion were calculated by the fluid-structure coupling method.Ultimate bearing capacities of box girder and ordinary warship compartment structure with plastic deformation damage under various impact factors were compared and analyzed by the damping factor method.The results indicate that under non-contact explosion, compared with ordinary deck structure,box girder structure is more advanced with smaller deformation and slower decreasing of ultimate bearing capacity after deformation, so that it can significantly improve the survivability of warship.
longitudinal box girder; ultimate bearing capacity; large deformation damage; non-contact explosion;damping factor method
U661.41
A
1673-3185(2011)01-22-08
10.3969/j.issn.1673-3185.2011.01.005
2010-04-06
王佳颖(1983-),男,博士研究生。研究方向:船体结构抗爆与极限强度。E-mail:www_frank@126.com
张世联(1952- ) ,男,教授,博士生导师。 研究方向:船舶结构力学。 E-mail:slzhang@ sjtu.edu.cn

