湍流边界层脉动压力波数—频率谱模型对比研究

王春旭 曾革委 许 建

中国舰船研究设计中心，湖北 武汉 430064

湍流边界层脉动压力波数—频率谱模型对比研究

王春旭 曾革委 许 建

中国舰船研究设计中心，湖北 武汉 430064

湍流边界层噪声是舰船主要水动力噪声之一。湍流边界层噪声预报须选用适当的脉动压力波数—频率谱模型。引入6种常用的脉动压力波数－频率谱模型，在波数域和频域内进行对比；运用这些模型对槽道流边界层脉动压力自功率谱进行预报，并引入试验结果进行对比，为工程应用中选择适当的脉动压力波数—频率谱模型提供依据：Corcos模型物理意义明确，但预报精度稍差；Chase模型表达式复杂，经验性更强，物理意义不明晰，预报精度较高。

湍流边界层噪声；波数—频率谱模型；脉动压力；自功率谱

1 引言

当舰船、鱼雷或者拖曳导流罩航行时，物面边界层由层流发展为湍流。湍流边界层为时间—空间上随机变化流动状态。湍流边界层内随机的速度扰动会产生随机的脉动压力，这种随机脉动压力一方面直接产生辐射噪声，另一方面激励物面弹性结构振动并产生辐射噪声，统称为“水动力噪声”。俞孟萨［1］对这个问题做过全面的综述。无论是计算湍流边界层脉动压力直接辐射噪声，还是预报其激励弹性结构振动而产生的辐射噪声，其方法仍是基于“声比拟”思想的，将边界层脉动压力作为“力源”代入到声比拟方程预报相应的辐射噪声。因此，如何定性定量地描述湍流边界层内部随机脉动压力是首要的问题，统计湍流理论是最适当的选择，采用频率—波数谱定量地描述这种面分布的时间空间随机脉动压力。频率—波数谱是通过大量的试验测量拟合出来的经验表达式。Corcos［2］、Efimtsov［3］、Smol’yakov 和 Tkachenko［4］、Ffowcs－Williams［5］、Chase［6－7］先后基于试验提出一系列被广为应用的频率—波数谱模型，各有特点。

本文将对6种常用湍流边界层脉动压力的波数—频率谱模型在波数域和频域进行对比，并将算例与试验结果对比，分析各种模型的特点、应用适用性及边界层湍流噪声预报方法。

2 边界层脉动压力频率—波数谱的比较

在如图1所示的坐标系统下，对于充分发展的平板湍流边界层，脉动压力频率—波数谱可以表示为 y、z 方向波数的函数Φ～p（ky，kz，ω），通常它是通过试验拟合得到的，并认为平板上各点边界层厚度完全一样。频率一定情况下，边界层内脉动压力的主要能量集中在 ky＝0，kz＝ω ／Uc附近，即所谓的迁移波附近，如图2所示。如何定量准确描述边界层的压力脉动频率－波数谱是边界层湍流噪声研究的重点。迄今为止，出现了多种频率波数谱模型，本文选取应用较多的6种进行分析。为了考察各自适用性，在相同条件下对其进行对比分析。

2.1 Corcos模型

Corcos首先拟合了窄频带边界层壁面压力相关函数，它是关于y、z方向的流动特征尺度ry、rz的函数，表达式如下：αy，αz是可选择的参数，用以与试验数据进行匹配。对ry、rz进行Fourier变换可得到边界层壁面脉动压力的频率—波数谱。需要注意的是，其中的壁面脉动压力功率谱密度Φ（ω）有多种选择，本文采用Blake［8］建议的方法，得到的壁面脉动压力的频率－波数谱如下：

不同的文献给出了多种 αy、αz取值，Blake 给出的值是 αy＝0.77，αz＝0.1。 Uc表示边湍流边界层内的迁移速度，一般取为：Uc＝0.7～0.8U∞。 已有的研究表明，采用Corcos模型预报边界层噪声，其低波数段往往过大。

2.2 Efimtsov 模型

Efimtsov模型沿用了Corcos模型的方法，但是在壁面脉动压力空间相关函数中引入了边界层厚度δ及尺度空间分离的影响，定义相关长度Λy＝ Uc/（|ω|αy），Λz＝ Uc/（|ω|αz）如下：

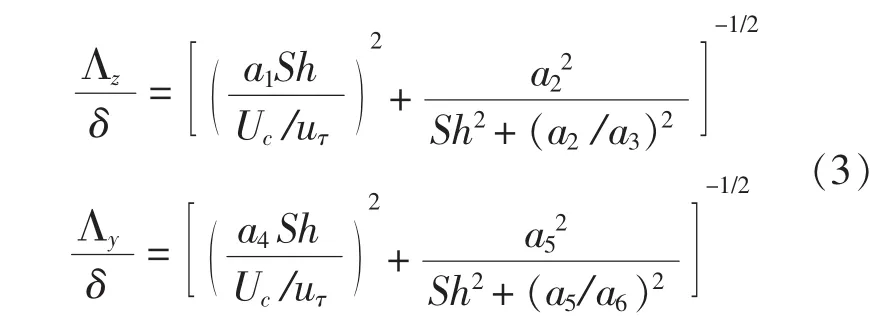
应用时，将式（2）中的参数 αy，αz分别用αy＝Uc/（|ω|Λy），αz＝ Uc/（|ω|Λz）。 其中，Strouhal数定义为Sh＝，uτ是摩擦速度。其中的常系数a1～a6分 别 取 值 如 下 ：0.1，72.8，1.54，0.77，548，113.5， 这对应于 Corcos 模型中 αy＝ 0.77，αz＝0.1的取值。

2.3 Smol’yakov 和 Tkachenko 模型

和 Efimtsov模型推导思路一样，Smol’yakov和Tkachenko模型在壁面脉动压力空间相关函数表达式中考虑了空间分离和边界层厚度的影响，最终拟合成指数形式函数。但是并不是将横向和纵向分离变量表达式做简单相乘，而是引入了指数因子－（/Λ+/）1/2，联合考虑空间分离的影响。对壁面脉动压力空间相关函数表达式做Fourier变换，得到其脉动压力频谱—波谱模型。与试验结果对比，较之Corcos模型，在低波数段有改进，但仍然偏高，因此引入一个修正项ΔF，使之在低波数段与试验结果吻合，但是不对迁移波附近造成大的影响。最终的频谱—波谱模型表示如下：

式中，δ* 是边界层位移厚度，取值为 δ*＝ δ／8。

2.4 Ffowcs－Williams模型

Ffowcs Williams从 Lighthill声比拟理论开始，并假定Lighthill方程右端的速度声源项是Corcos形式，得到一个频谱—波谱模型，包含多个未知参数及函数，至今未完全确定，需要进一步更精细的试验确定。其中常用的一个简化模型，忽略了可压缩性，对其中的未知函数做了一些假定，形成的表达式形式上是对Corcos模型进行修正：

2.5 Chase 模型Ⅰ

Chase采用和Ffowcs－Williams相同的方法，应用了一些更具体更具启发性的假定得到一个边界层脉动压力频谱—波谱模型：

根据Chase的建议，其中的参数取值如下：CM＝ 0.074 5，CT＝ 0.047 5，h ＝ 3.0，bM＝ 0.756，bT＝0.378。

2.6 Chase 模型Ⅱ

Chase模型Ⅰ在两个方面存在着不足：其一是在气动声学领域它不能涵盖超音速域（|kz|＜ω/c0）；其二它也不能描述在试验中观察到的低波数段（ω／c0＜kz＜ω／Uc）“白波数”现象。为了改善后一种缺陷，Chase解除了低波数段的波数—频率谱对波数依赖，即Φ～p（k，ω）|k|2，给出了一种改进的频谱波谱模型：

与Chase模型Ⅰ相比较，FM仍然是严格的，FT则进行了简化，其他的参数建议使用如下：h＝3.0，hCM＝ 0.466，hCT＝ 0.014，b ＝ 0.75。

2.7 频率—波数谱波数域比较

为了考察以上各种模型的适用性和特点，固定 Ma＝ 0.003 3，边界层厚度为 0.1 m，在不同频率下比较上述各个模型波数—频率谱结构。

图3给出的是Sh＝666，ω＝999时6种脉动压力波数—频率谱的比较；图4对应的是Sh＝266，ω=399的情况；图 5对应的是 Sh＝66，ω＝99的情况，图6对应的是Sh＝26、ω＝39的情况。横坐标是流向方向的波数，用迁移波波数无量纲化。纵坐标表示脉动压力谱幅值。

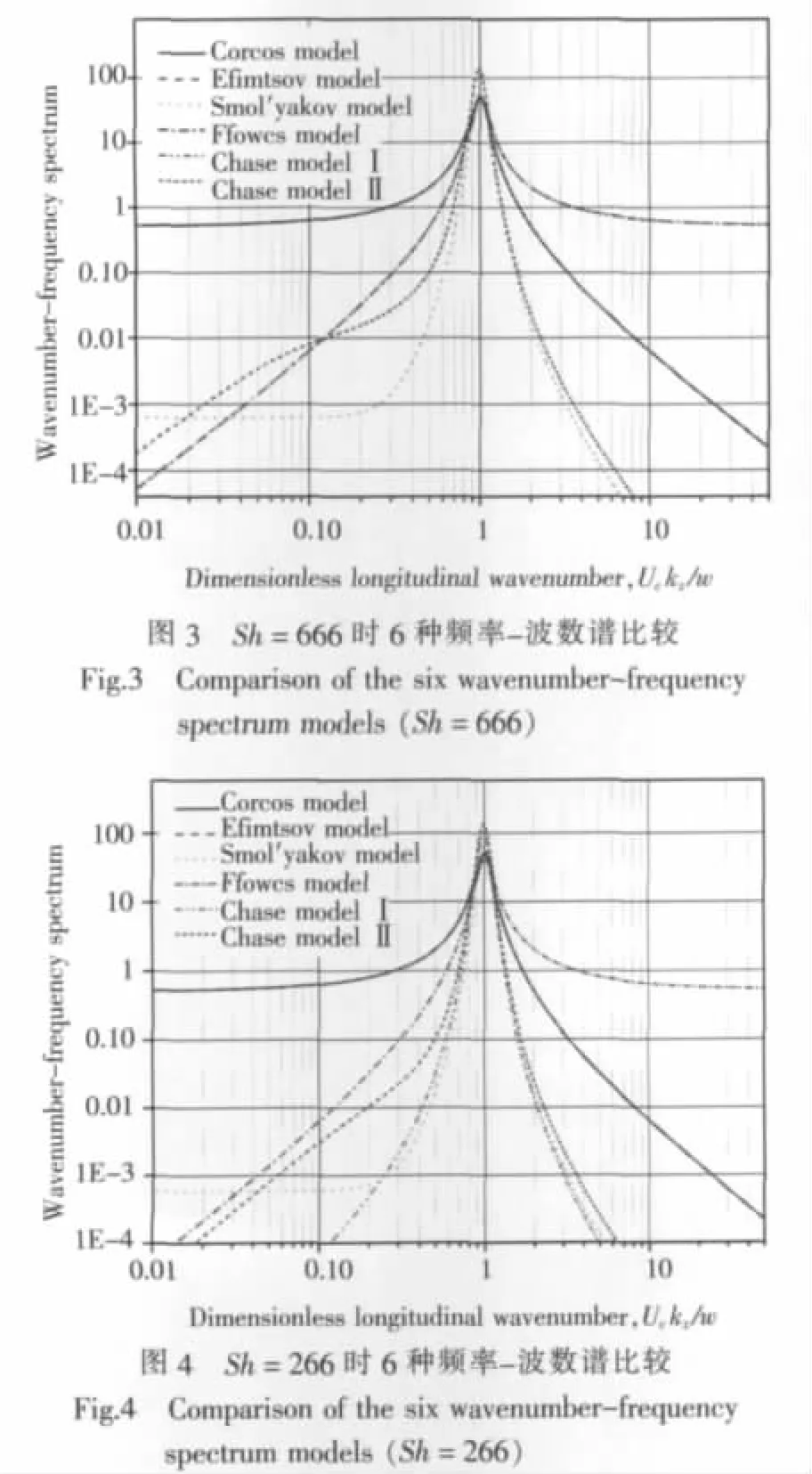
在中高频段（Sh＝666，Sh＝266），Corcos模型和Efimtsov模型完全重合，在迁移波附近预报声级和其他模型相似，在低波数段，较之其他模型，预报声级要高出很多。Smol’yakov和Tkachenko模型联合考虑了横向和纵向空间分离作用，并引入修正因子，使得其迁移波附近波数－频率谱结构比其他模型要窄，在低波数段值也较小。在低波数段，均能体现试验中观察到的“白波数”现象。

在低频段（Sh＝66，Sh＝26），边界层厚度的影响显现出来，Corcos模型没有考虑边界层厚度δ的影响，与高频时相比，几乎没有改变。而Efimtsov模型由于其相关尺度变小，迁移波显著变宽，波峰迅速减小。Smol’yakov和Tkachenko模型的相关尺度也受到边界层厚度的影响，但对迁移波变宽度和峰值影响均较小。

Ffowcs Williams模型较之Corcos模型，低波数段减小，高波数段增大，但基本不受频率影响，在各频率下谱结构基本保持不变。

频率减小，Chase模型Ⅰ和Chase模型Ⅱ差别变小，趋近于一致。在高频时能看到Chase模型Ⅱ相对于Chase模型Ⅰ在低波数段的 “白波数”现象，低频时不明显。

3 湍流边界层脉动压力自谱预报

3.1 边界层脉动压力自功率谱预报方法

为了进一步考察第2节6种频率－波数谱模型的噪声预报的特点及其优劣，在此采用这6中模型对湍流边界层脉动压力自功率谱进行预报，并与试验结果进行对比。

对于选定的湍流边界层压力脉动的波数—频率谱，边界层脉动压力自功率谱可以如下给出［9］：

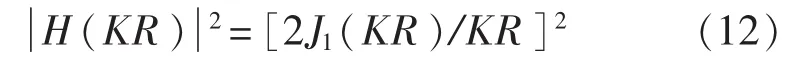
式中，J1第一类一阶Bessel函数；R是传感器半径

3.2 槽道流数值模拟

利用式（11）预报边界层脉动压力自功率谱，需要先对Horne和Handle槽道流进行数值模拟，提取相关流场信息。

第2节中六种波数—频率模型、式（11）所要用到的流场信息有：边界层厚度、边界层对流速度、摩擦速度、位移边界层厚度。因此，并不需要知道流场详细的细节，非稳态雷诺平均（URANS）方法足以提供上述需要的结果。另一方面，尽管Horne和Handle试验的槽道流是一个三维问题，但是该槽道截面形状比较大，而且并不需要知道流场模拟的结果细节，因此可以将问题简化为二维问题。

标准k－ε模型封闭雷诺应力是URANS方法最常用的形式，但是该模型是针对充分发展湍流建立的，在壁面附近，常需采用壁面函数，不利于应用。本文中的数值模拟采用Jones和Launder［12］提出的低Re数k－ε模型，控制方程全流域都适用，近壁区域不再使用壁面函数。

将控制方程式采用一阶混合格式离散。采用基于交错网格的SIMPLE算法进行计算。其他计算参数如下：无穷远来流速度 U＝0.7 m／s，取流体运动粘性系数ν ＝ 1.05 × 10－6m2／s。 计算起始点 x＝1.25 m处速度剖面用1／7幂次率剖面模型给出。计算流场长度为1.5 m。

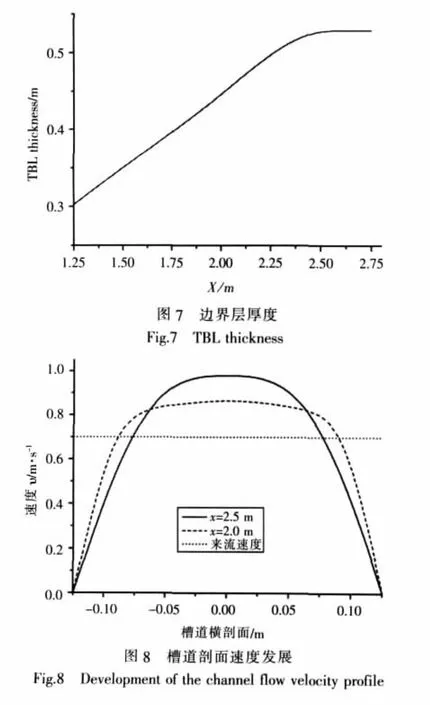
图7给出的是边界层厚度发展，边界层厚度是用来流速度 U＝0.7 m／s定义的。大约在 x＝2.55 m处以后，边界层厚度保持不变。

图 8给出了 x＝2.0 m 和 x＝2.5 m 处的速度剖面，从中可看出边界层的发展。

3.3 槽道壁面湍流脉动压力自谱预报

Horne和 Handle［11］在美国海军研究试验中心（NRL）的矩形截面水槽中测量了湍流边界层脉动压力自功率谱。水槽矩形截面尺寸为457 mm×25 mm（18∶1），所用两个圆形传感器的直径为 0.5 mm，间距为 2H，在雷诺数 Rh＝UH／υ＝25 000 （U为槽道中心线最大速度，H为槽道高度）情况下，测量的脉动压力自谱如图9～图11中实线所示。可见，边界层脉动压力自功率谱主要表现为0.1～1 kHz的连续谱，在高频段脉动压力自谱衰减很快。

根据3.2节槽道流数值计算结果及式（11），即可用第2节6种波数—频率谱模型计算槽道边界层脉动压力自功率谱并进行比较。

图9是Corcos模型和Efimtsov模型边界层压力脉动自谱预报以及与试验的比较。从该图可以看出，Corcos模型和Efimtsov模型预报边界层压力脉动自谱基本相同，在低频方向稍有差异，与图3～图6结论一致；与试验数据相比，在频段1～100 Hz，规律和量级上比较都吻合，但在该频段两端，吻合度比较差，特别是在高频方向，这两个模型预报值最后都趋于常数，这与式（1）中壁面脉动压力功率谱密度Φ（ω）的选择有关。

图 10是 Smol’yakov模型和 Ffowcs Williams模型边界层压力脉动自谱预报以及与试验的比较。Ffowcs Williams模型式（6）可以看作是对Cor-cos模型式（1）的修正，与图 9 Corcos模型和E-fimtsov模型预报结果相比，这种修正作用很大，特别是在高频段，与试验结果吻合较好。

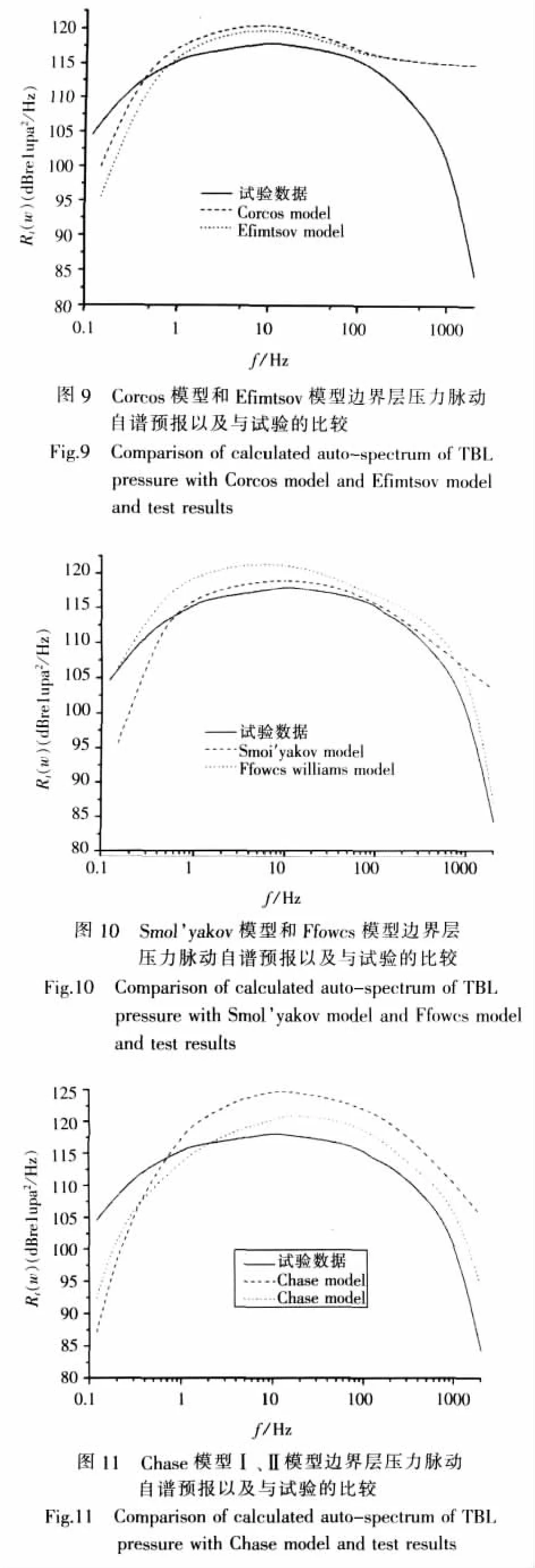
图11是Chase模型Ⅰ、Ⅱ边界层压力脉动自谱预报以及与试验的比较。与试验结果相比，Chase模型Ⅰ、Ⅱ在频谱结构和量级上都有较好的吻合度，Chase模型Ⅱ更优。

4 结论

本文引入了6种常用的边界层脉动压力波数—频率谱模型，在频域和波数域对比分析各模型特点。运用这些模型对某槽道流TBL脉动压力自谱进行预报并与试验数据进行对比，分析各模型适用性。得出相关结论可供工程应用参考。

一般性结论是：Corcos模型及在此基础上发展的模型形式简单，推导过程中物理意义明确。但是在低波数段、低频段、高波数段或者高频段不稳定，影响噪声预报结果。Chase模型根据试验结果进行了大量修正，表达式复杂，更经验化，已不具备明确物理意义，但是准确性较好。

［1］俞孟萨，吴有生，庞业珍.国外舰船水动力噪声研究进展［J］.船舶力学， 2007， 11（1）： 152－158.

［2］CORCOS G M.The structure of the turbulent pressure field in boundary－layer flows ［J］.Journal of Fluid Mechanics，1964，18（3）：353－378.

［3］EFIMTSOV B M.Characteristics of the fields turbulent wall pressure fluctuations at large Reynolds numbers［J］.Soviet Physics－acoustics，1982，28（4）：289－292.

［4］SMOL’YZKZV A V，TKACHENKO V M.The Measurement of turbulent fluctuation［M］.Springer－Verlag，1983.

［5］FFOWCS－WILLIAMS J E， Boundary layer pressures and the Corcos model：a development to in corporate low wavenumber constrains ［J］.Journal of Fluid Mechanics，1982（125）：9－25.

［6］CHASE D M.Modeling of the wavevecter－frequendy spectrum of turbulent boundary wall pressure ［J］.Journal of Sound and Vibration， 1980（70）：29－67.

［7］CHASE D M.The character of the turbulent wall pressure spectrum at subconvective wavenumber and a suggested comprehensive model［J］.Journal of Sound and Vibration，1987（112）：125－147.

［8］BLAKE W K.Mechanics of flow induced sound and vibration 1 Complex flow structure interaction ［M］.New York：Acadamic Press，1986.

［9］CAPONE D E.Calculation of turbulent boundary layer wall pressure spectra ［J］.The Journal of Acoustic Society of America，1995，98（4）：2226－2234.

［10］KO S H.Performance of various shapes of hydrophones in the reduction of turbulent flow noise ［J］.The Journal of Acoustic Society of America，1993，93（3）：1293－1299.

［11］HORNE M P， HANDLER R A.Note on the cancellation of contaminating noise in the measurement of turbulent wall pressure fluctuations ［J］.Experiments in Fluids，1991（12）：136－139.

［12］JONES W P， LAUNDER B E.The calculation of low－Reynolds－number phenomena with a two－equation model of turbulence ［J］.International Journal of Heat and Mass Transfer， 1973（16）：1119－1130.

A Comparative Study of Models for the Wavenumber-Frequency Spectrum of TBL Fluctuation Pressure

Wang Chun－xu Zeng Ge－weiXu Jian
China Ship Development and Design center，Wuhan 430064，China

The Turbulent Boundary Layers （TBL） noise is one of the major components of hydrodynamic noise.For prediction of the TBL noise， however it requires a suitable model of the wavenumber－frequency spectrum of TBL fluctuation pressure，so choosing a most appropriate model becomes substantially important.Six kinds of wavenumber－frequency spectrum models were introduced and compared in frequency domain and wavenumber domain in this study.The auto－spectrum of TBL pressure of a channel was calculated with the six models as mentioned above， and also compared with the experimental results.Some of available results are presented for practical use.The study shows that the Corcos model has definite physical significance but less accuracy， other than Chase model， which is empirical and has much more complicated expression， but usually leads to more accurate results with the experimental＇s.

TBL noise； wavenumber－frequency spectrum model； TBL fluctuation pressure； auto－spectrum

U661.44

A

1673－3185（2011）01－35－06

10.3969/j.issn.1673-3185.2011.01.007

2010-07-20

“十一五”装备预研课题（51310040402）

王春旭（1981－），男，博士。研究方向：舰船声隐身技术。E-mail：chxwang＠ yahoo.cn

曾革委（1968－），男，博士，研究员。研究方向：舰船声隐身技术。

许 建（1966－），男，博士，研究员。研究方向：舰船声隐身技术。