基于波面随机性的船舶底部砰击压力计算方法研究
陈 震 肖 熙
上海交通大学 船舶海洋与建筑工程学院,上海 200030
基于波面随机性的船舶底部砰击压力计算方法研究
陈 震 肖 熙
上海交通大学 船舶海洋与建筑工程学院,上海 200030
基于海浪波面的随机特性,研究船舶底部砰击压力的计算方法。分析纵向入水角对船底砰击压力量值的影响程度,建立二者之间的定量关系。在预报船舶砰击压力时引入随机海浪的波面条件,计及船舶运动和海浪波面倾角因素对砰击压力的影响。采用蒙特卡罗数值模拟法对砰击压力的统计规律进行研究,结果表明:计及纵向入水角的船底砰击压力计算方法,更加合理地反映波面条件和船底波面形状等因素的影响。
船舶底部砰击;波面随机性;纵向入水角;蒙特卡罗法
1 引言
在过去的几十年里,船舶砰击方面研究取得了很大进展,但是仍有一些与砰击相关的基本问题未完全解决,例如船舶底部砰击的临界相对速度至今尚无明确的物理解释[1];静水落体试验和船模适航性试验结果相差甚大,海浪波面条件对砰击压力的影响程度未知等。当发生砰击时,船舶底部纵向龙骨线与波面之间存在一定夹角,该夹角使得船体各横剖面并非同时入水,而是自船中至首部各剖面依次撞击波面。船舶发生砰击时船底龙骨线与波面夹角具有随机性,砰击压力大小不仅与船底横剖面形状有关,还应考虑船舶运动和波面条件等因素。 Ochi和 Schenzle[2-3]开展的船模砰击试验充分说明波面条件对船舶底部砰击压力量值的影响。
本文研究船舶运动和海浪波面条件对船舶砰击压力的影响,讨论了静水落体试验与船模在波浪中砰击试验结果差异的原因,通过引入纵向波倾角参数,计及波面条件对砰击压力的影响,并根据船舶在波浪中的运动和海浪波面斜率等随机变量的统计特性,采用蒙特卡罗数值统计试验的方法研究了船底砰击压力的统计值和概率密度函数。
2 船舶砰击纵向入水角
船舶底部发生砰击时船底龙骨线与波面之间的夹角定义为纵向入水角。纵向入水角由船舶纵摇角、海浪波面倾角和船舶初始倾角组成(图1)。
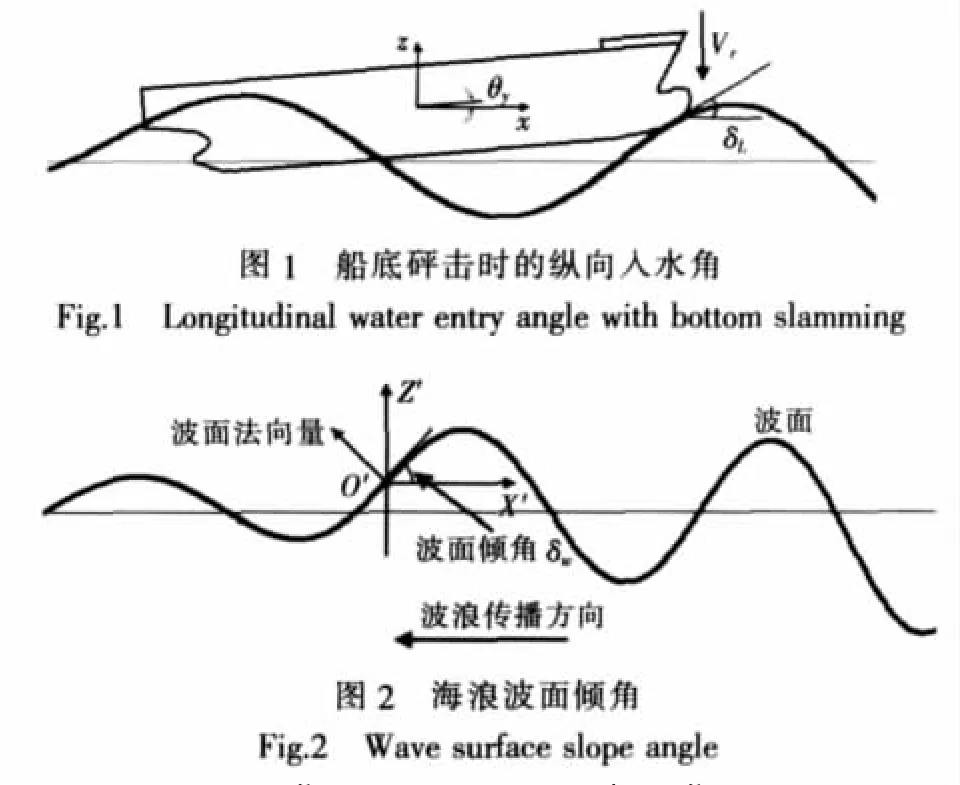
如图1所示,迎浪情况下船舶砰击纵向入水角为:

式中,δL为纵向入水角;δw为波面倾角,迎波面为正;θy为船舶纵摇角;θk为船底龙骨线初始倾角,即非正浮的船舶首尾倾角。
船舶在航行过程中,船舶运动纵摇角和海浪波面倾角均随机变化,因此纵向入水角也为随机变量。将船舶在随机海浪中运动视为窄带随机过程,瞬时值近似服从正态分布。
海浪波面倾角反映了波面的局部斜度,波面局部斜度并非均匀,波峰附近要比其他处大得多。对于任意时刻不规则海浪,波面倾角为该时刻波面位移与水平X轴之间的夹角。波面位移是正态随机过程,作为波面位移线性变换的波面斜率服从联合正态分布。若将波浪看成二维长峰波,可得出二维海浪波面斜率的概率密度函数[4-5]:
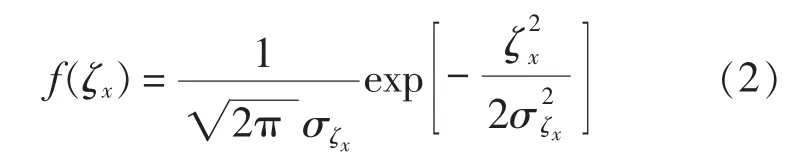
式中,ζx为 x 方向的波面斜率;σ为x方向波面斜率的方差。
海浪波面倾角随机变量的概率密度函数可从波面斜率密度函数推导得出。根据波面倾角和波面斜率的关系 δw=arctg(ζx),由随机变量函数的概率密度函数计算和式(2),导出波面倾角的概率密度函数[6]为:
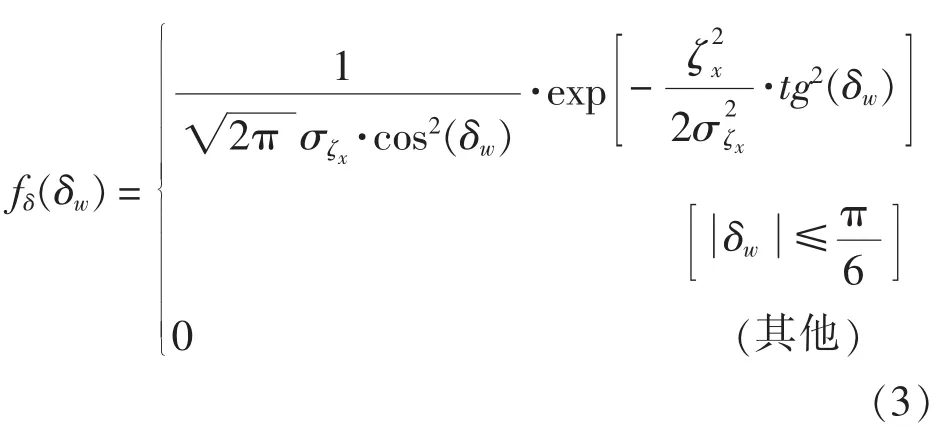
3 考虑纵向入水角的船底砰击压力计算
试验和理论研究表明,砰击压力大小与入水砰击速度平方成正比[7],计算公式为:

式中,ρ为水密度;k1为无因次形状系数;Vr为砰击瞬时垂向相对速度;
式(4)中形状系数k1和砰击瞬时垂向相对速度Vr是确定砰击压力大小的重要参数。对于船底入水砰击而言,砰击压力系数取决于底部横剖面形状 (特别是1/10设计吃水以下部分船体形状)和波面条件等因素。
3.1 纵向入水角对砰击压力的影响
纵向入水角包含船舶运动纵摇角和波面倾角的因素,对砰击压力大小的影响程度通过分析锥形体与楔形体入水试验结果得出。锥形体是规则三维落体,在垂直于XY平面各个方向具有相同的入水角,锥面与X轴方向夹角α和与Y轴方向夹角β相等,即α=β=0。楔形体是两维落体,与X轴方向夹角α=0,与Y轴夹角为β。两种落体入水,在斜面上产生的最大冲击压力有明显差异,Chuang[7]根据试验测得的结果绘制曲线见图3。
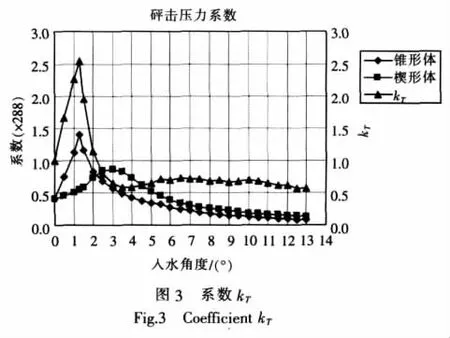
在相同斜升角的情况下,在斜升角小于2°时,锥形体远大于楔形体入水冲击压力。升角大于1°以后,锥体表面压力迅速降低,入水角大于2°后,锥形体压力低于楔形体的压力。楔形体入水角大于6°,锥形体入水角大于4°时,空气垫效应微弱。
将相同斜升角时锥体表面压力系数与楔形体表面压力系数的比值kT作为该角度下纵向倾角对楔形体入水砰击压力的影响程度,则有:

式中,kW为楔形体静水落体砰击压力系数。
值得注意的是,图3中的kT曲线在0°~2°段纵向入水角对楔形体砰击压力具有放大作用,这是由于空气垫对二维落体和三维落体缓冲效应的不同造成的。这种情况只有在船体横剖面斜升角与纵向入水角均很小,空气层明显被捕获的情况才会显现。
式(5)将波面倾角因素与落体剖面形状两个因素分离开加以考虑,由船体纵向入水角和船底剖面形状分别确定系数kT和kW。系数kT则反映了由于船舶纵摇运动和波面倾角引起的纵向入水角对砰击压力的影响程度,形状系数kW来源于静水落体试验,只取决于落体剖面形状,与船舶运动和波面的不规则程度无关。
3.2 船底剖面砰击压力系数的确定
在预报船底砰击压力大小时,需要根据船底剖面形状确定砰击压力系数,进而由式(4)、式(5)计算砰击压力量值。式(5)中形状系数为一定斜升角的楔形体入水试验测量结果,船底剖面形状与规则的楔形体有一定差别,导致这二者所受到的砰击压力特点会有一定差别[8]。以下讨论由船底剖面形状确定形状系数。
为了能在船舶设计初期阶段利用某些简单参数快速计算砰击压力系数,选取船舶底部基本的参数包括1/10吃水,水线半宽、平底半宽和水线下剖面面积作为基本参数用来确定砰击压力系数。根据以上参数,设计不同的剖面形状,采用Ochi砰击压力系数回归公式研究各参数对砰击压力系数的影响程度。
图4为某船1/10吃水以下船底剖面扩展图,为了研究平底宽度对砰击压力系数的影响程度,将原先15站、16站、17站原始型线扩展为8条型线,每组型线平底半宽WF与水线半宽WB自0.1~0.8,根据Ochi回归公式计算各条型线的砰击压力系数绘于图5。

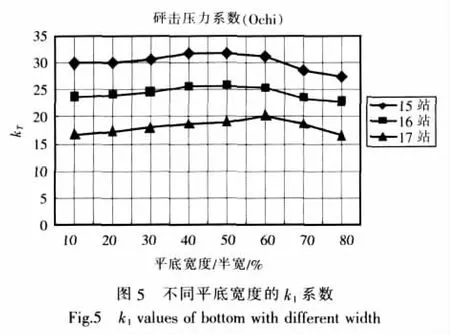
平底半宽对砰击压力系数k1的影响程度不是很大,对砰击压力量值大小主要取决于船底剖面的宽度吃水比。在根据船底剖面形状确定砰击压力系数时,由船底中心与舷侧1/10吃水高度处连线倾角作为楔形体斜升角,确定砰击压力系数是合理的。
4 算例
本文以某集装箱船为例,计算了船舶在实际海况下船首底部砰击压力统计值,并与Ochi方法进行了比较。集装箱船的主尺度数据列于表1,图6为其线型情况。
计算了该船在7级海况(有义波高7.8 m)和8级海况(有义波高为10.5 m)下船舶运动响应和船波相对速度。表2为海浪波面斜率方差和各航速时船舶纵摇角方差计算结果。

表1 主尺度数据Tab.1 Main dimensions
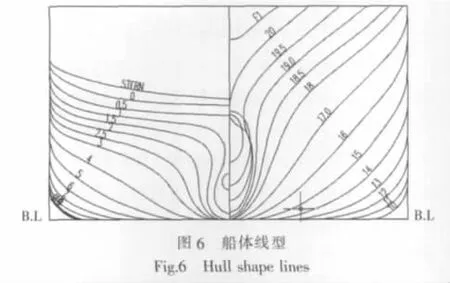

表2 波面斜率和船舶纵摇运动响应计算结果Tab.2 Calculation results of motion response and wave slope at different sea states
在垂向相对速度相同的情况下,由于纵向入水角因素的影响,船底砰击压力仍为随机变量,其概率特性取决于海浪波面条件和船舶运动情况。本文采用蒙特卡罗随机抽样法[9]研究在垂向相对速度相同的情况下,底部砰击压力的统计规律。
根据海浪波面斜率、船舶纵摇角随机变量的概率密度函数生成随机数[10]。随机数为10 000个,由式(1)计算船舶砰击纵向入水角,并由此确定系数 kT,根据式(4)、式(5)计算得出系列底部砰击压力值,对此砰击压力系列进行统计计算分析。
图7分别为8级海况下海浪波面倾角和纵向入水角的频次直方图和正态分布拟合曲线,由图中可见,海浪波面倾角和纵向入水角基本上能够较好地符合正态分布规律。

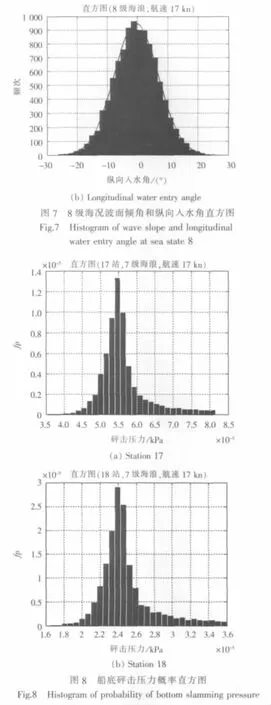
图8为17站、18站船底砰击压力概率直方图,相对速度取十分之一最大平均值。在船首底部即使以相同相对速度发生砰击,砰击压力仍具有一定随机性,其概率特性与海浪波面条件以及船舶运动情况有关。船首17站、18站、19站船底砰击压力概率直方图极值所对应的砰击压力分别为546 kPa、239 kPa 和 188 kPa, 累积概率为 0.57、0.52和 0.62。从概率意义上讲,该砰击压力是在实际观测中出现概率最大的数值。
表3中列出了7级、8级海况下17~19站船首底部砰击压力的统计平均值,并给出了根据Ochi理论计算的结果。Ochi根据船模适航性试验测得的砰击压力回归值普遍大于考虑纵向入水角影响的船舶砰击压力有义值,与十分之一最大平均值较接近。

表3 砰击压力统计值Tab.3 Statistics value of slamming pressure(kPa)
5 结论
本文研究了海浪波面条件对船底砰击压力的影响,提出了考虑纵向入水角因素的船底砰击压力计算方法,讨论了在船波之间具有相同相对速度时砰击压力随机变量的概率特性。通过本研究得到如下结论:
1)海浪波面条件是解释二维落体试验与船模适航性试验砰击压力较大差异的重要原因,在计算船底砰击压力时应计及该因素的影响;
2)考虑纵向入水角的船底砰击压力计算方法,更加合理地反映波面条件和船底剖面形状等相关因素;
3)在随机海浪中,船波之间具有相同相对速度时砰击压力并非定值,而是服从一定概率分布的随机变量,其概率特性与海浪波面条件和船舶运动有关。
[1]胡嘉骏,蔡新钢.船舶表面点砰击压力的预报方法[J].船舶力学:2005,9(1):63-70.
[2]OCHI M K, MOTTER L E.Prediction of slamming characteristics and hull responses for ship design[J].SNAME,1973:144-176.
[3]OCHI M K,MOTTER L E.Prediction of extreme values of impact pressure associated with ship slamming [J].China Ocean Engineering,Journal of Ship Research,1969 (13):86-91.
[4]XU D L,LIU X H,ZHANG J.Statistical distribution of surface slope in a 3-D ocean wavefield [J].China Ocean Engineering,2000,14(3):289-296.
[5]徐德伦,楼顺里,赵锰,等.一种海浪破碎的判别方法[J].海洋学报,1990,12(5):648-653.
[6]陈震,张世联,肖熙.船舶外飘砰击有效砰击角概率分布[J].上海交通大学学报,2010,44(10):1405-1408.
[7]STAVOVY A B,CHUANG S L.Analytical determination of slamming pressures for high-speed vehicles in waves[J].Journal of Ship Research,1976,20(4):190-198.
[8]陈铁云,王刚.高速船舶结构设计中流体冲击载荷的数值计算[J].上海交通大学学报,1998,32(11):30-33.
[9]尹增谦,管景峰.蒙特卡罗方法及应用[J].物理与工程,2002,12(3):45-49.
[10]朱晓玲,姜洁.任意概率分布的伪随机数研究和实现[J].计算机技术与发展,2007,17(12):116-118.
Calculation Method of Bottom Slamming Pressure Based on Randomness of Wave Surface
Chen Zhen Xiao Xi
School of Naval Architecture,Ocean and Civil Engineering,Shanghai Jiaotong University,Shanghai 200030,China
The paper studied the prediction method of ship bottom slamming pressure based on the randomness of ocean wave surface.The effect of longitudinal angle between keel and wave surface on slamming pressure was analyzed and the quantitative relationship was established.The factors of ship motion and inclination angle of wave were considered by introducing wave surface condition while calculating slamming pressure of ship bottom.Monte-Carlo simulation method was used to study the statistics characters of slamming pressure with the same relative velocity between ship sections and wave surface.The results show that the method of ship bottom slamming pressure calculation considering the longitudinal angle can properly reflect the influences of factors in terms of wave surface condition and bottom wave surface.This study provides the foundation for a further study of extreme value of slamming pressure at short-term sea state.
ship bottom slamming;wave surface randomness;longitudinal water entry angle; Monte-Carlo simulation
U662.2
A
1673-3185(2011)01-07-05
10.3969/j.issn.1673-3185.2011.01.002
2010-04-16
国家自然科学基金资助项目(50709018);高等学校博士学科点专项科研基金资助课题
陈 震(1976-),男,博士,副教授。研究方向:船舶与海洋工程现代强度理论与结构设计。E-mail:chenzhen@ sjtu.edu.cn

