三维数字空间法与波叠加法结合的近场声辐射计算
熊济时 吴崇健 徐志云 曾革委
中国舰船研究设计中心,湖北武汉 430064
三维数字空间法与波叠加法结合的近场声辐射计算
熊济时 吴崇健 徐志云 曾革委
中国舰船研究设计中心,湖北武汉 430064
传统的波叠加法是边界元法的有效替代方法,其具有计算速度快计算精度较高等优点,但是也有复杂模型的建立较困难,以及对模型适应性较差等缺点。为了克服传统波叠加法的缺点,从而使其能够计算较为复杂模型的声辐射,将三维数字空间方法与传统波叠加法结合,因为三维数字空间方法具有建模迅速,对模型适应性很好等优点。分别采用边界表示法和体积表示法建模,且通过简单算例计算表明,采用这两种方法与传统波叠加法结合计算外场声辐射是完全可行的,并且结果的精确度相对较高,采用边界表示法的效率相对较高。
声辐射;波叠加法;边界表示法;体积表示法
1 引言
对于振动体的外场声辐射问题,目前最常用到的数值方法是有限元(FE)和边界元(BE)方法[1-4],这两种方法极大地加速了声辐射问题的工程发展。但它们有明显的不足,即对不同阶的奇异积分要做相应数值处理,当遇到具有解非唯一性的特征波数时,对该奇异积分的处理更加困难。为了寻找边界元的有效替代方法,20世纪80年代末,Koopmann 等[5-6]和 Miller等[7]提出了基于简单源替代的波叠加方法 (Wave Superposition Method,WSM)。其主要思想是:任何物体辐射的声场可以由置于该辐射体内部若干个简单源产生的声波场叠加代替,而这些简单源的源强可以通过匹配辐射体表面上的法向振速得到。在声辐射问题中,场中的声压和质点振速必须同时满足波动方程和辐射体表面上的边界条件,而波叠加方法就是寻求近似解来满足这样的边值问题。该方法通过在声辐射体内放置若干个满足波动方程的声源,来近似表面上的边界条件,这种方法被证明等效于Helmholtz积分方程,也就是说和边界元方法在理论上是一致的。该方法由于不需要求解边界积分方程,从而避免了繁琐的各阶奇异积分处理,大大降低了数值实现的难度,且更易于理解和在工程上进行推广。
从理论上讲,波叠加法适合于计算任意光滑表面物体的声辐射,计算平台通常选择Matlab,因为Matlab是当今世界上使用最为广泛的数学软件,它具有相当强大的数值计算、数据处理、系统分析、图形显示,甚至符号运算功能,是一个完整的数学平台,在这个平台上,你只需寥寥数语就可以完成十分复杂的功能,大大提高了工程分析计算的效率[8]。对于形状相对简单的物体,可以很方便地在Matlab上进行建模,但是如果物体的外形很复杂,在Matlab上建模则变得很困难。另外,如果物体外形变化,则相应的计算程序要做较大的改动,即传统的WSM方法的外形适应性不好,为了解决这一问题,Zellers[9]和 Hwang[10]采用了一种简单的三维数字空间方法来建模,然后运用基于实际边界的波叠加方法来求解物体的声辐射。这种方法的最大优点是建模迅速,对模型外形的适应性非常好,另外这种方法能够较好的解决边界奇异值的问题,但是计算精度没有传统的WSM方法高。为了充分发挥传统WSM方法和三维数字空间方法的优点,本文将传统的WSM方法与三维数字空间方法结合来求解三维物体的声辐射,即采用三维数字空间方法来建模,然后运用基于虚拟边界的波叠加方法来求解物体的声辐射。
2 传统的波叠加方法
由线性欧拉方程和叠加积分,辐射体表面的速度可以用下式来表示:
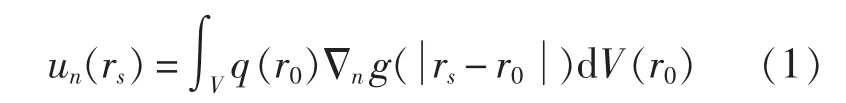
式中,rs是S表面点的位置矢量;q(r0)是辐射体内虚拟源分布在点 r0处的源强值;g(r,r0)为自由场的格林函数。对于复杂结构而言,很难找到其解析解,因此有必要对其进行离散。连续分布的虚拟源可以由N个离散的点源来取代,再在辐射体表面选取M个离散点,获取其法向加速度值,则辐射体表面某点的法向速度可以表示如下:

式中,Qi是第i小段的源强,由N个简单声源可以构建复杂振源的表面法向速度,而表面法向速度un(rs)是已知的,因此式(2)可用于计算每个简单源的源强Qi。假设一共获知N个点上的法向振速,那么将其构成一个N维列向量U,并将虚球源上的N个点源的源强构成一个N维列向量Q,将它们之间的关系写成矩阵形式:

D是M×N的传递矩阵,其表达式如下:
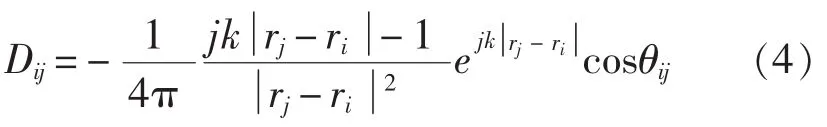
当M>N时,即可获得方程的唯一解,获得虚拟点源源强之后,再通过式(5)可以计算得到任意点的声压:

其中,M为单极矩阵,其与自由格林函数成正比。
3 三维数字空间方法
数字表达意味着计算机图形,所有的图像都用离散的像素来表示,而无需真实形状的数值或理论信息,这意味着为了在计算机域中表示一个物体,必须将物体转化为离散的形式。三维数字空间方法即是以离散像素来表示具体的物体。具体实现的方法有两种,一种是边界表示法,即将表面表示成一系列的三角形或者四边形的细小平面;另一种是体积表示法,即将物体的体积以细小的体积单元代替。如图1所示,分别给出了一个圆球的两种表示方法。

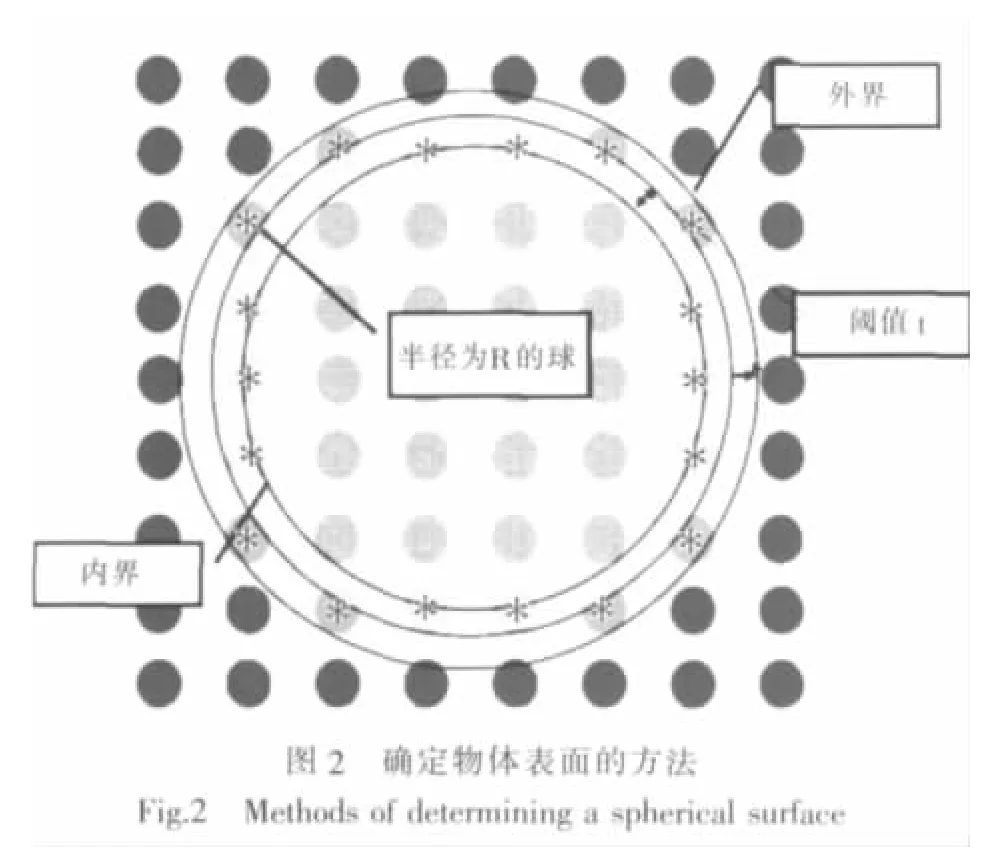
上图给出了三维物体的数字表示信息,而在波叠加法中只需要给出物体表面的信息,因此首先需要描述物体的表面,与通常的有网格方法不一样,边界表示法只是提取物体表面的节点信息来描述物体的表面,而无需考虑表面单元的信息;而体积表示法通常有两种描述方法,一种是直接从划分网格的软件导入,例如从ANSYS、PATRAN、I-DEAS等;另一种是采用理论方法来描述一个物体的表面,通常是一些比较规则的表面如球面、椭球面等。两种方法都需要设置一个如图2所示的阈值(阈值越大则选中的节点数越多,所描述的表面却越不真实,阈值越小则选中的节点数越小,但是所描述的表面却越真实,但是如果节点数太少,计算精度则可能受到影响),将符合阈值要求的节点认定为表面节点。图2给出了第二种方法确定物体表面的方法,图中红色带*点组成的图形用来近似描述球表面。Zellers[5]和Hwang采用了体积表示法来建模,然后运用基于实际边界的波叠加方法来求解物体的声辐射。
4 数值计算
由于脉动圆球的声辐射有解析解,因此本文采用脉动圆球作为计算模型,所有计算均在MATLAB7.0平台完成,圆球半径取为1 m,表面脉动速度为1 m/s,计算了距离实际边界表面1 m距离处的声辐射 (本文定义的近场为距离实际边界表面1 m处),分别采用边界表示法和体积表示法来求解。
4.1 边界表示法
由于在文献[8]中已经做过虚拟源半径与实际边界半径之间关系的研究,研究表明虚拟源半径取到实际边界的0.2倍时,即可满足计算要求。因此本文首先通过ANSYS软件前处理器建立半径分别为1 m和0.2 m的两个物理模型,并将两个模型分别划分网格,分别在ANSYS中提取两个模型的外表面节点坐标,半径为1圆球的节点坐标定义为(X,Y,Z),它表示实际边界的节点坐标;半径为 0.2 m 圆球的节点坐标定义为 (x,y,z),而它则表示虚拟边界的节点坐标;然后分别将其保存为两个文本文档 1.txt和 2.txt;再将这些节点信息导入MATLAB;最后根据公式(4)计算得到虚拟源与振动源表面之间的振速传递系数矩阵D,根据式(3)计算得到虚拟源的源强值,根据式(6)得到单极系数矩阵,就可以根据式(5)算出外部辐射声场。
4.2 体积表示法
本文与Zellers和Hwang一样,也采用体积表示法建模,但是采用传统的WSM方法来求解声辐射。首先将三维空间划分为细小的晶格,然后将在网格文件导入或者直接用理论方法描述的物体置于划分好的三维空间当中,设置阈值,找出符合阈值条件的节点;再将符合条件的所有节点按一定比例缩小,使新得到的节点位于实际物体边界内部,作为虚拟边界节点;最后根据传统的WSM方法生成矩阵并且求解得出外部辐射声场。
4.3 结果及讨论
首先我们给出脉动圆球外场声辐射的解析解(无量纲声压)表达式如下:

式中,a为圆球的半径;r为外场中某点与球心之间的距离(r=2 m);p(r)为距离 r处的声压;k 是波数。再分别按照上述步骤,采用边界表示法和体积表示法也计算出脉动圆球的外场声辐射。
假定数值计算得到的无量纲声压实部为per,无量纲声压虚部为pei,对应的无量纲声压解析解分别为pr和pi,则实部误差εr和虚部误差εi分别为:
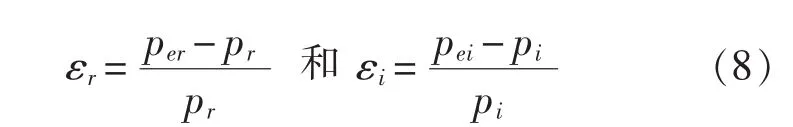
采用边界表示法时,分别考虑了两种情况,第一种情况是半径为1 m球表面包含114个节点,半径为0.2 m球表面也包含114个节点;第二种情况是半径为1 m球表面包含114个节点,而半径为0.2 m球表面包含78个节点,计算结果如图3所示。图3a为脉动圆球数值解与解析解之间的误差随波数变化实部,图3b为脉动圆球数值解与解析解之间的误差随波数变化虚部,数值解的实部和虚部在波数为0~20范围内基本上都与解析解相吻合,误差很小。虚拟边界表面节点选取较多时,计算精度较高,但是在ka=15.7≈5*pi时,最大实部误差达到了1%左右,最大虚部的误差更是达到了10%以上,这是因为脉动圆球的特征波数为pi的整数倍。

采用体积表示法时,将三维空间划分为边长为0.02 m的立方体格子,然后将半径为1 m球置于三维空间当中,设置阈值为10-6,找出符合阈值条件的表面节点,共150个,然后将这些表面节点按0.2的倍数缩减,重新得到150个小球的表面节点,最后将半径为1 m球表面的节点作为实际边界节点,而半径为0.2 m球表面边界节点作为虚拟边界节点,分别代入传统波叠加方法,求解出脉动圆球的声辐射。图4给出了采用体积表示法时,数值解和解析解之间误差的实部和虚部。结果同样示出了波数为0~20范围内的误差值,从图中可以看出,实部和虚部的误差值都非常小,均在0.1%以下,结果的精度要显著高于Hwang给出的结果。

从图3和图4来看,只要边界节点选择恰当的话,边界表示法和体积表示法均能得到较好的结果。边界表示法只需要构造辐射体的表面,在进行数字空间构造时网格处理量较少,而体积法则需要构造出整个辐射体,在进行空间构造时处理的网格数通常非常大,构造工作量相对较大(本文当中的晶格数量为50×50×50=125 000),因此边界表示法比体积表示法效率更高。
5 结束语
传统的WSM方法是一种声辐射的无网格计算方法,其具有计算速度快,精度较高的优点,但是其外形适应性不是太好,对于复杂模型的建立难度较大,因此对于工程推广应用有一定的限制。三维数字空间方法则具有建模迅速,对模型外形的适应性非常好等优点。本文将两者结合用于求解外场声辐射,并以具有解析解的脉动圆球声辐射算例来验证了方法的可行性,以及此种计算方法的结果具有较高精度这一特性。
[1]谭林森,骆东平,吴崇健,等.潜水器动力舱振动与声辐射[J].华中理工大学学报,1999,27(11):7-9.
[2]徐张明,沈荣瀛,华宏星.利用FEM/IBEM计算流体介质中的壳体的结构声耦合问题 [J].振动工程学报,2002,15(3):363-367.
[3]徐张明,汪玉,华宏星,等.船舶结构的建模及水下振动和辐射噪声的FEM /BEM计算 [J].船舶力学,2002,6(4):89-95.
[4]商德江,何祚镛.加肋双层圆柱壳振动声辐射数值计算分析[J].声学学报,2001,26(3):193-201.
[5]KOOPMANN G H,SONG L,FAHNLINE J B.A method for computing acoustic fields based on the principle of wave superposition[J].Journal of Acoustic Society America,1989,86(6):2433-2438.
[6]SONG L,KOOPMANN G H,FAHNLINE J B.Numeric errors associated with the method of superposition for computing acoustic fields [J].Journal of Acoustic Society America,1991,89(6):2625-2633.
[7]MILLER R D.A comparison between the boundary element method and the wave superposition approach for the analysis of the scattered fields from rigid bodies and elastic shells [J].Journal of Acoustic Society America,1991, 89(2):2185-2196.
[8]熊济时,吴崇健,曾革委,等.基于波叠加法的近场声辐射研究 [C]//2009年第22届全国振动与噪声高技术及应用学术会议,2009:135-140.
[9]ZELLERS B C.An acoustic superposition method for computing structural radiation in spatially digitized domain[D].USA:The Pennsylvania State University, 2006.
[10] HUANG Y S.A wave superposition method formulated in digital acoustic space [D].USA:The Pennsylvania State University,2009.
Near-Field Sound Radiation Numeration Based on Wave Superposition Method in the 3D Digital Space
Xiong Ji-shi Wu Chong-jian Xu Zhi-yun Zeng Ge-wei
China Ship Development and Design Center, Wuhan 430064, China
The traditional Wave Superposition Method (WSM) may be substituted for the Boundary Element Method (BEM) because of its capabilities of rapid computation and greater precision.However,with merely reliance on mesh geometry,it cannot accommodate fast shape changes in the design stage of a consumer's product or machinery, where a great amount of iterations of shape changes are required.In order to overcome these shortcomings of WSM,a new approach to representing geometry was introduced by constructing a uniform lattice in the 3D digital work space.With this method, geometry was represented with boundary nodes or small lattice that can easily adapt to shape changes and therefore is more suitable for shape optimization.The boundary representation and volume elements representation method respectively combined with WSM were validated by computing sound radiation of simple structures.The results show that both methods are entirely capable of handling this calculation,and have higher precision, in addition, the boundary representation method exhibits higher efficiency than volume element representation method.
sound radiation; wave superposition method; boundary representation method; volume elements representation method
O422.6
A
1673-3185(2011)01-41-05
10.3969/j.issn.1673-3185.2011.01.008
2010-03-12
船舶工业国防科技预研基金(08J1.4.3)
熊济时(1977-),男,博士研究生。研究方向:噪声与振动控制。E-mail:xiong26@163.com
吴崇健(1960-),男,研究员,博士生导师。研究方向:噪声与振动控制

