一类半波对称FFT改进算法与电网谐波分析

汤天浩，郑 慧

（上海海事大学电力传动与控制研究所，上海200135）

引言

由于电力电子技术的飞速发展，各种电力电子装置普遍使用，谐波所造成电力系统污染等危害也日趋严重。因此，近年来，电能质量控制研究已被人们逐渐重视，成为国际电气工程领域的研究热点之一。电能质量控制的问题涉及面很广，而谐波测量和谐波分析是研究电能质量问题中的一个重要分支，也是解决谐波问题和治理电网污染的出发点和主要依据。

长期以来，傅里叶变换（FT）一直是研究分析谐波的经典方法和有效工具，也广泛用于电力系统的谐波测量分析中。随后又发展了用离散傅里叶变换（DFT）或快速傅里叶变换（FFT）进行频谱分析进而得到各次谐波幅值和相位。在实际应用当中，电网谐波分析就是通过对信号进行同步采样，将周期信号展开为傅里叶级数，得到各次谐波系数进而进行各项谐波指标的计算，如THD，HRn等。

然而，FT不具有时域分析能力，对含有短时高频分量和长时间低频分量的电能质量信号进行分析时具有局限性。为了改善FT的局限性，1994年出现了窗口FT即后来的短时FT算法，比如：矩形窗、三角形窗、汉宁窗、海明窗、布莱克曼窗等。但是短时FT的时频窗口是固定的，不适于分析信号的突变过程，且其离散形式没有正交展开，难以实现高效算法。

本文首先通过对DFT与周期信号傅里叶级数以及非周期信号FT之间关系的研究，得到了用FFT对非周期信号进行精确谐波测量的公式。进而，针对一类电网波形具有半波对称性的特点，提出了一种改进的FFT算法。改进的FFT算法对于只含奇次谐波分量的一类半波对称性波形，在算法流程中省去了偶次谐波分量部分。因此，改进的FFT算法的计算量是传统FFT的一半，大大节省了运算时间。

1 快速傅里叶变换算法

1.1 DFT基本算法[1]

对于对N点序列x(n)，其DFT变换定义为：

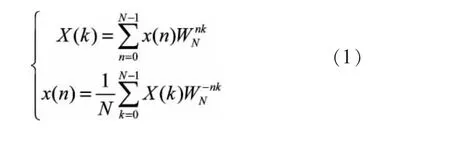
显然，求出其N点X(k)需要N2次复数乘法及N(N－1)次复数加法。而实现一次复数乘法需要四次实数乘两次实数加，实现一次复数加则需要两次实数加。当N很大时，其计算量是相当可观的。

由于上式中W因子的取值具有如下特点：

（1） W0=1，WN/2=-1；

（2） WNN+r=WrN，WN/2+r=-Wr。

因此，在DFT中包含了大量重复运算，如果能够巧妙地利用W因子的周期性及对称性，将大大减少运算量。

1.2 基于频率抽取得的FFT算法

FFT算法最早由Cooley和Tukey于1965年提出，该算法使N点DFT的乘法计算量由N2次降为N/2log2N。自Cooley-Tukey的算法提出之后，FFT的发展方向有两个：一是针对N等于2的整数次幂的算法，如基2算法、基4算法等；二是以Winograd为代表的一类N不等于2的整数次幂的算法。近年来，又不断涌现许多新的算法，比如：由A.M.Grigoryan等人提出的流图简化算法[2]。

如果采用时间抽取（DIT）基2 FFT算法，将频域 X(k)的序号 k按奇、偶分开，对式（1）的 DFT，先将x(n)按序号分成上、下两部分，得：

式中：WNNk/2=（-1）k；k＝0，1，…，N－1。

分别令 k＝2r，k＝2r＋1，可以推导出奇、偶两个计算序列：

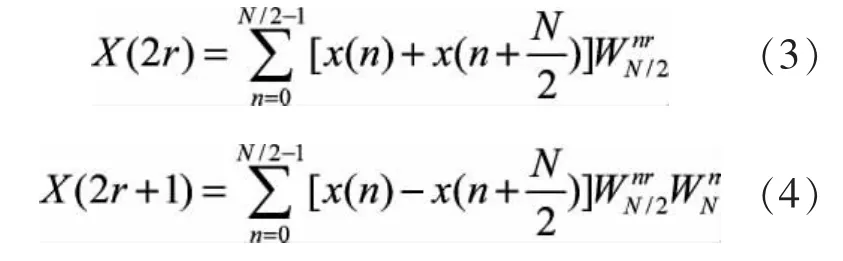
这样就将一个N点DFT分成了两个N/2点的DFT，分的办法就是将X(k)按序号k的奇、偶分开。

2 基于半波对称的DIF基2FFT改进算法

2.1 FFT算法及特点

由上节对频率抽取（DIF）基2 FFT算法的分析可知，该算法是将每一组计算得到的输出序列按奇、偶分开而得到的一种快速傅里叶变换算法。而且，通常FFT算法都是全波分析和计算，即同时计算各次谐波，包括奇次谐波和偶次谐波。

2.2 基于半波对称FFT算法的提出

为研究电力系统谐波，需先分析电力系统谐波的产生根源及其特点。电力系统的谐波主要是由于电力电子装置等非线性负载的大量使用造成的，且具有如下特性[3]：

（1） 奇对称性的特点是 f(－t)＝－f(t)，展开为傅里叶级数时没有余弦相。

（2） 偶对称性的特点是 f(－t)＝f(t)，展开为傅里叶级数时没有正弦相而只有余弦相。

（3） 半波对称的特点是 f(t±T/2)＝－f(t)，没有直流分量且偶次谐波被抵消。

因为电力系统往往是由双向对称的元件组成的，这些元件产生的电压和电流具有半波对称性[4]，这类半波对称特点使我们在谐波分析时可以忽略电力系统中的偶次谐波。

如果考虑一类电力系统谐波的半波对称特性，并利用DIF的基2 FFT算法的奇、偶序列的可分性，对频率抽取（DIF）基2 FFT算法进行改进，可得到一个只计算奇次谐波的用于电网谐波分析的快速傅里叶变换算法。

2.3 一类半波对称的DIF基2FFT计算方法

考虑到一类电力系统的电压和电流具有半波对称性，其偶次谐波被抵消。因此仅需在上节给出的DIF基2FFT算法中，仅需进行奇序列计算。但X（2r+1）仍然是高复合数（N/2）的 DFT，对 X（2r+1）仍然按照式（2）进行分解，即：

分别令 r＝2l，r＝2l+1，l＝0，1，…，N/4－1。 有：

式中：l＝0，1，…，N/4－1。

例如：N＝8，则有 l＝0，1，这时 f(n)和 i(n)都是两点的 DFT，无需再分。 将 l＝0，1 代入式（10）和（11）有：

这样，我们就得到了8点DFT的奇次谐波。若N＝16，32或2的更高的幂，可按上述方法继续分下去，直到两点的DFT为止。

2.4 算法的实现

2.4.1 算法的实现

改进的算法仍然是基于频率抽取 （DIF）基2 FFT算法的，即：在每一级都对频域序号k按照奇、偶分开，直到两点的DFT为止。其抽取过程可用一个树形图来表示，如图1所示，由于改进算法是不计算偶次谐波的，因此图2中只对奇次谐波进行抽取。

图1 改进算法的树形图

整个算法的关键是计算每一级所对应的g(n)，h(n)，f(n)，i(n)，…，对照图 1，可以画出每一级所对应的 g(n)，h(n)，f(n)，i(n)，…，的树形图，如图 2 所示。 由于只需计算奇次谐波部分，因此可以直接从X(2k+1)作为第一级开始往下分，每一级所对应的h(n)，f(n)和 i(n)，…，均用 h(n)，h1(n)，h2(n)，…，来表示。 图中m 表示第 m 级，m＝1，2，log2N－2。 l表示第 m 级所需要计算的 h(n)的个数，即 h1(n)，h2(n)，…，hl(n)，l＝1，2，…，2m。

2.4.2 码位倒置

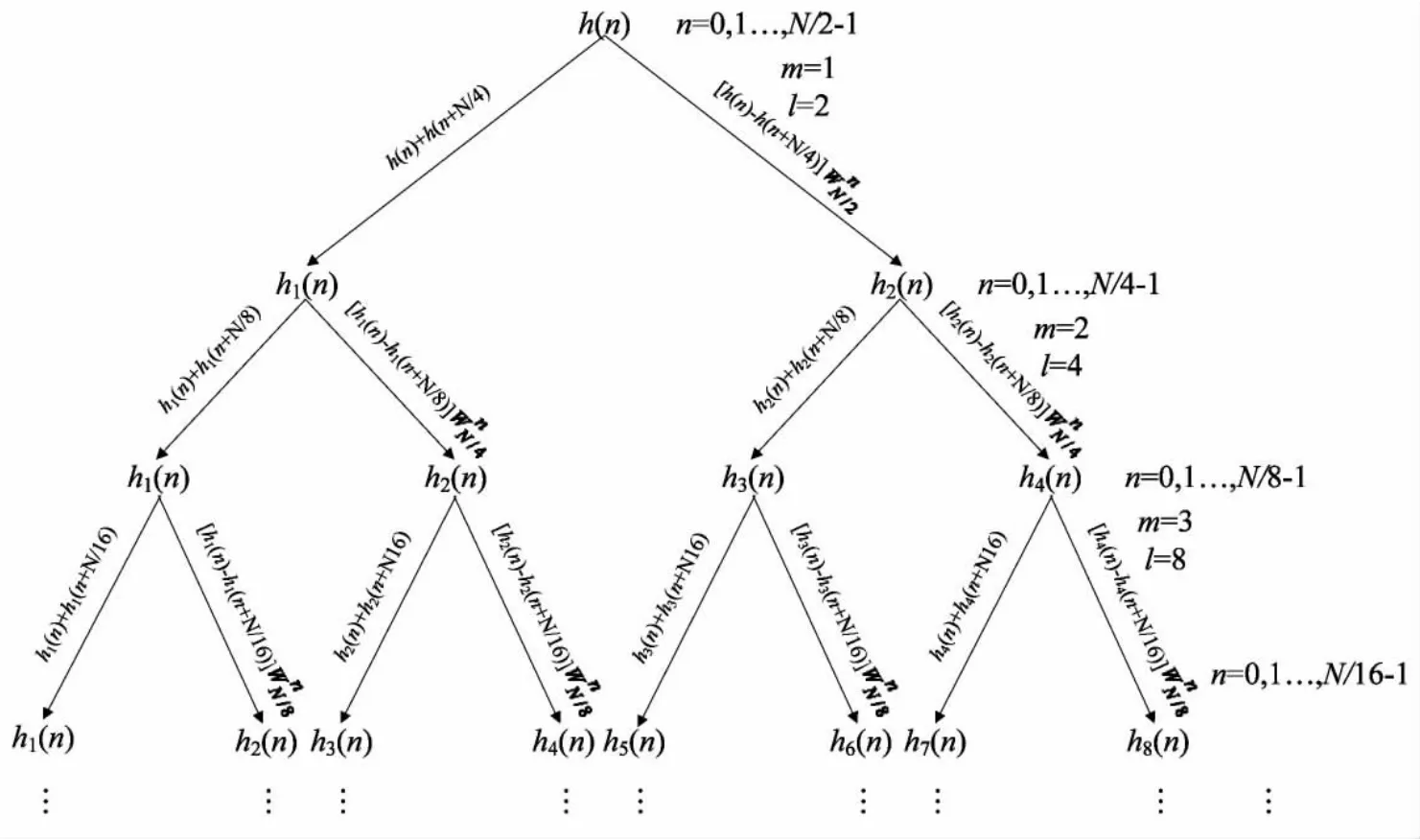
图2 改进算法的树形图

由频率抽取信号流图，其变换后输出序列X(k)的次序不再是原来的自然顺序，如果将输出X(k)的序号写成二进制，并将二进制数码翻转，它们对应的十进制序号这正是我们需要的自然顺序输出。在改进算法中，只计算了奇次谐波分量，对于直流分量和偶次谐波分量可以直接令其为零，这是因为在半波对称波形中不含直流分量和偶次谐波分量。这样在编程的时候，前N/2点数据直接赋值为0，而后面N/2点就等于前面计算出来的各奇次谐波分量，对于这样的N个数据，我们就可以利用码位倒置的规律，最后得到X(k)的自然输出序列。图3给出了只有奇次谐波的16点DIF基2 FFT改进算法流程图。

图3 输出只有奇次谐波的16点DIF基2 FFT改进算法

2.5 算法比较

在MATLAB下编写了该改进算法的程序——half_dif.m，并通过对方波信号的仿真分析，证明了该程序的正确性。表1给出了方波信号谐波的理论值、用一般FFT分析的谐波值以及用改进算法进行分析的谐波值，这里，为方便比较，只给出了其中直流分量、基波分量和2到15次谐波的幅值。

表1 方波信号（0—15次）谐波幅值表

通过比较可以发现，利用改进算法进行谐波分析，其奇次谐波跟一般FFT分析的结果是一致的，而偶次谐波则跟理论值是一致的，与前面的理论分析是相吻合的，从而证明了该程序的正确性。

3 电力系统谐波分析实验

本文利用matlab里面的GUI向导设计器设计了一个用于电网谐波测量分析的人机交互界面，可以实现如下功能：

（1）可以由用户确定滤波器截止频率、阶数以及滤波器型号，其中包含了三种基本滤波器：巴特沃思滤波器、切比雪夫I型滤波器和椭圆滤波器。

（2）由用户输入一周期采样点数N。

（3）实现对一些基本信号的谐波测量分析，

（1），（2）所确定的滤波器以及采样点数都是针对这些基本信号的。基本信号包括：方波信号、矩形信号和正弦加3次、7次谐波信号，其中正弦信号幅值为1，相位为0，而3次、7次谐波幅值均为0.5，3次谐波相位为π/2，7次谐波相位为0，如图4所示。（1），（2）都是用于基本信号的谐波测量分析。

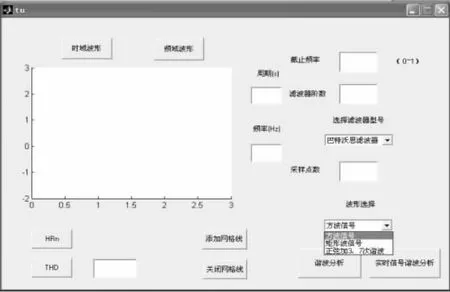
图4 三种基本信号波形选择界面图

实现对实时信号的谐波测量分析，如图5所示。其中图5（a）为对逆变器一相输出电压的测量波形，图5（b）为谐波分析结果。

图5（a） 逆变器输出电压时域波形显示界面图

图5(b) 各次谐波含有率波形显示界面图（正弦加3，7次谐波信号）

4 结论

本文根据一类电网信号具有半波对称性的特点，提出了一种用于电网谐波测量改进的快速傅里叶变换算法，该算法的计算量是传统FFT算法的一半，因此大大减少了运行时间；在对改进算法进行详细推导的基础上，详细介绍了算法的实现过程；并完成了在matlab下对改进算法的程序的编写，该程序在matlab里面可以像其工具箱里面的FFT函数一样直接被调用；进而通过电网谐波分析实验，验证了所提方法的可行性。

[1] 胡广书.数字信号处理――理论、算法与实现[M].北京：清华大学出版社，2003.

[2] Artyom M Grigoryan，Veerabhadra S Bhamidipati.Method of Flow Graph Simplification for the 16-Point Discrete Fourier Transform[J].IEEE Transaction on Signal Process,2005,53(1):384-359.

[3] George J Wakileh（奥地利）著，徐政译.电力系统谐波——基本原理、分析方法和滤波器设计[M].北京：机械工业出版社，2003:4-21.

[4]Marek ROGó z˙.Model of the Harmonic Analyzer for the Needs of Power Quality Assessment[A].In:Proceedings of the 8thInternational Conference on Electrical Power Quality and Utilisation[C].Cracow,Poland,2005:21-23.

[5]Hui Zheng,Zhao Chen,Dongkai Peng and Tianhao Tang.A Variable N Synchronous Sampling Method for Grid Aperiodic Harmonic Detection and Analysis[A].In:Proceedings of ICFPEE2010[C].Shenzhen,China,2010.