基于非线性观测器的DFIG直接功率控制

刘金山，张 淼，陈思哲

（广东工业大学 自动化学院,广州 510006）

引言

由于化石能源的日渐枯竭和环境污染的日益严重，大规模开发以风能为代表的各类可再生能源，已经成为人类社会实现长期可持续发展的必然选择。

基于双馈感应电机(DFIG)的风力发电机组，具有灵活调节有功和无功功率、实现最大风能捕获、减小机械应力和提高电能质量等优点，而且其变流器只需传输滑差功率，容量小、成本低，因此在大功率风力发电中得到广泛应用[1]。

功率控制技术是DFIG风力发电机组控制中的关键问题。国内外许多学者对DFIG的功率解耦控制进行了深入的研究，文献[2-4]设计了基于定子磁链定向的功率解耦控制方法，文献[5,6]设计了基于定子电压定向的功率解耦控制方法，以实现对有功和无功功率的独立调节。

由于矢量控制依赖电机精确参数，文献[7,8]设计了DFIG的直接转矩控制方法。直接转矩控制具有动态响应快且不依赖电机参数等优点，然而滞环控制会产生开关频率不固定和电流畸变等问题，影响输出电能质量[9]。

参照直接转矩控制的原理，文献[10]提出DFIG直接功率控制(DPC)方法。由于该方法依旧采用滞环控制，因此仍无法解决功率变换器开关频率变化所引起的谐波问题。文献[11]在DPC中引入空间矢量调制技术，提出了开关频率固定的DPC方法，在每个固定的时间周期内，根据定子磁链、转子位置、功率参考值和实际值的偏差直接计算出功率变换器应输出的转子电压矢量，从而使开关频率固定，改善了输出电能质量。在此基础上，文献[12]提出了基于转子磁链、转子电流和电磁转矩的三种开关频率固定的DPC控制策略。

本文在传统DPC的基础上，设计了跟踪微分器(TD)和状态观测器，以改善系统的动态性能。仿真结果表明，与传统DPC方法相比，本文提出的基于非线性观测器的DPC方法能有效地解决快速性与超调量之间的矛盾，实现快速无超调控制，同时减小动态过程中有功功率和无功功率间的相互影响，具有更好的动态性能。

1 DFIG的数学模型

图1 为基于DFIG的风力发电机组结构。DFIG的定子绕组直接与电网连接，转子绕组由双PWM变换器励磁，其中转子侧变换器用于控制DFIG，而网侧变换器主要用于稳定直流侧电容电压。

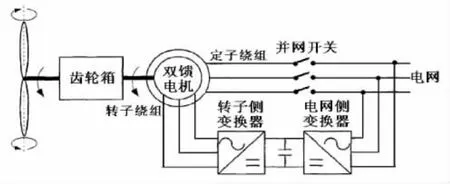
图1 基于DFIG的风力发电机系统

在同步旋转坐标系中，DFIG的电压方程为：

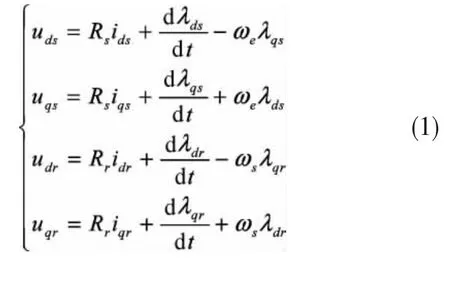
DFIG的磁链方程为：

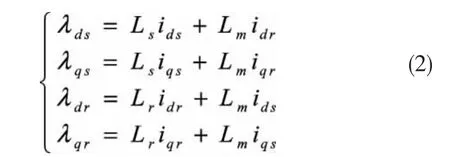
其中，ωs=ωe-pnωr，Ls=Lls+Lm，Lr=Llr+Lm。

上述各式中：u，i，λ分别表示电压、电流、磁链；Rs，Rr分别表示定、 转子电阻；Lm，Lls，Llr分别表示定转子互感、定子漏感、转子漏感；ωe表示同步转速，ωr表示转子速度，ωs表示转差速度，pn表示极对数；下标 d，q分别表示 d，q轴， 下标 s，r分别表示定、转子。

根据DFIG数学模型可绘出其等效电路如图2所示[13]：

令同步旋转坐标系的d轴与定子磁链矢量重合，忽略定子电阻的影响，当电网电压幅值恒定时，有

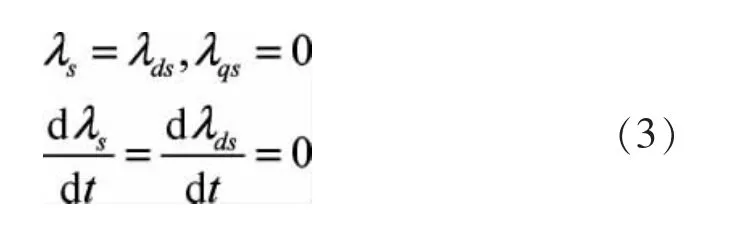
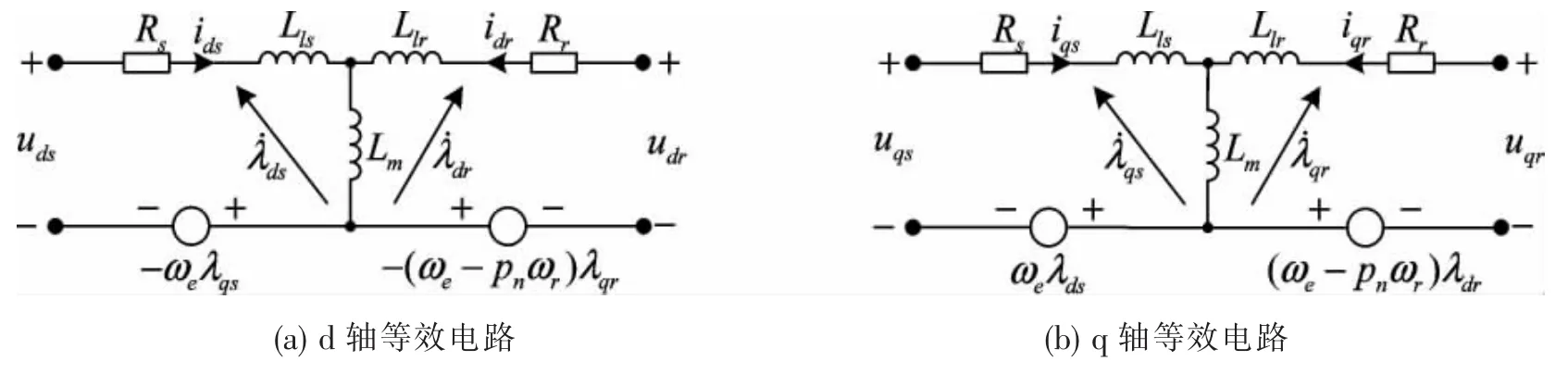
图2 同步旋转d-q坐标系中DFIG的等效电路

把（3）式代入（1）式可得并网后的定子和转子电压方程：

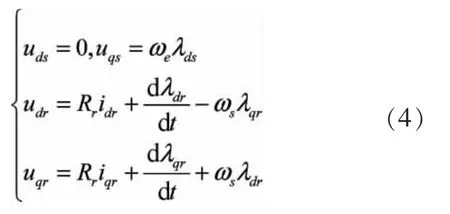
由式(2)、(3)、(4)可以计算出定子有功和无功功率为：

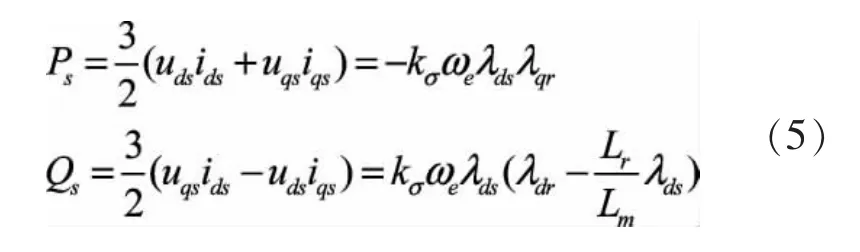
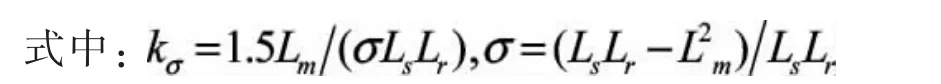
整理(4)、(5)式，忽略转子阻抗得到功率控制的微分方程为：

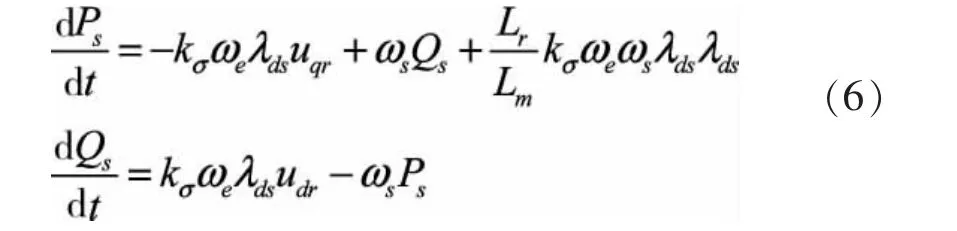
2 基于非线性观测器的DPC设计

2.1 跟踪微分器（TD）

对TD输入信号v(t)，它将输出2个信号z11和z22，其中 z11跟踪 v(t)，而 z*11=z11，从而把 z22作为 v(t)的“近似微分”。其作用是根据参考输入v(t)和受控对象的限制来安排过渡过程，得到光滑的输入信号，并提取出此过渡过程各阶导数的动态环节。跟踪微分器的算法公式为：

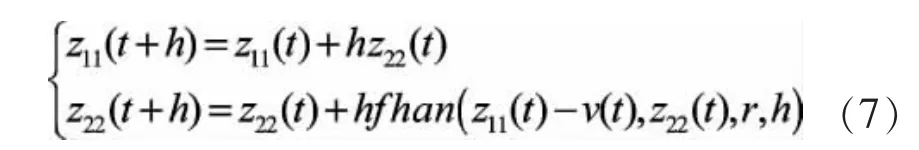
fhan（z11（t）-v（t），z22（t），r，h）为如下非线性函数：

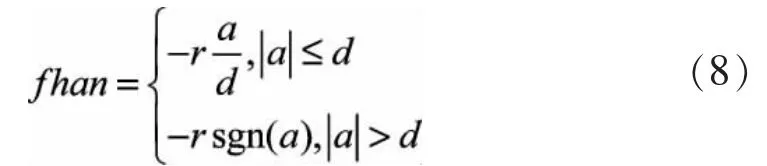
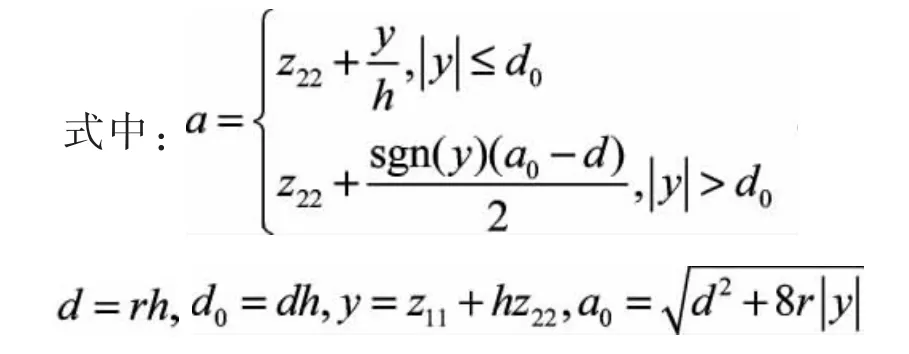
上述各式中r和h为可调参数。输入信号v(t)在系统中为有功功率给定P*s和无功功率给定Q*s，输出信号z11,z22在系统中显示为：P*11,P*22和Q*11,Q*22。

2.2 非线性状态观测器

状态观测器的作用是有效跟踪其观测的状态变量及其各阶“广义微分信号”。本系统中输入y为测得的有功功率Ps和无功功率Qs,输出z1,z2为有功功率Ps1，Ps2和无功功率Qs1，Qs2。其算法公式如下：

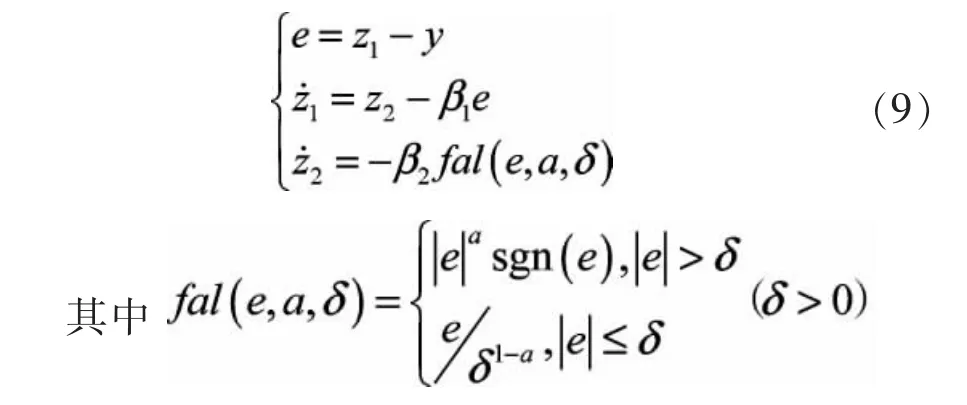
2.3 控制器结构

系统的原理框图如图3所示。

系统主要由四部分组成：信号检测、状态观测器、跟踪微分器、功率解耦和功率控制器。

（1）信号检测。定子三相电压和电流通过坐标变换转化为静止坐标系下的电压和电流，由静止坐标下的定子电压和电流根据式(10)估算出定子磁链及其同步旋转速度，根据式(11)在静止坐标系中直接计算出定子有功和无功功率。

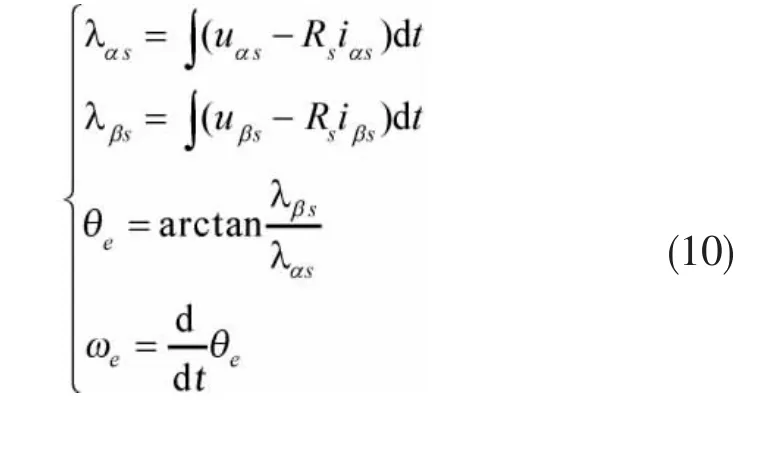
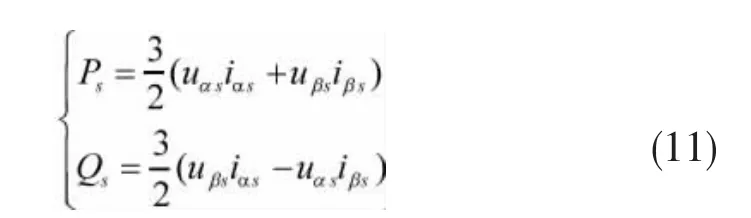
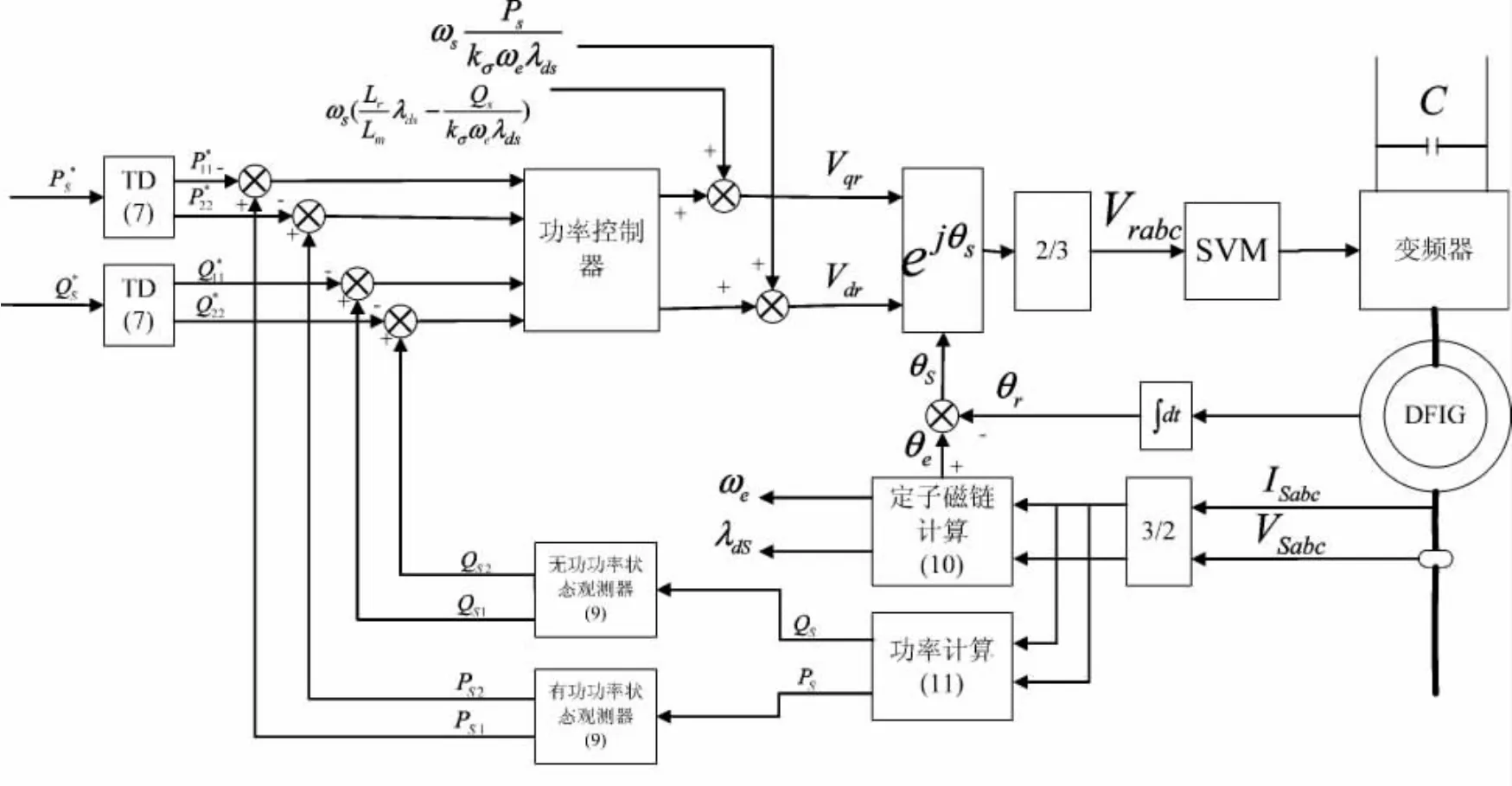
图3 基于非线性观测器的DPC原理框图

（2）状态观测器。利用式（9）构造的非线性状态观测器对DFIG的有功、无功功率进行状态观测估算。

（3）跟踪微分器。通过式（7）的跟踪微分器得到给定有功和无功功率的过渡状态指令信号。

（4）直接功率控制。采用比例控制器控制系统的有功、无功功率及其近似微分状态分别跟踪有功、无功功率指令及指令的近似微分状态；通过前馈补偿消除有功和无功功率间的交叉耦合；通过坐标变换将转子电压从同步坐标系变换到转子坐标系，并通过SVM模块控制转子侧变换器。

3 仿真验证

在本文前面介绍的内容基础上，运用Matlab/Simulink分别对传统DPC和基于非线性观测器的DPC进行仿真研究。仿真模型中DFIG参数如下：额定功率1.8 kW，额定频率50 Hz，同步转速1 500 RPM，定转子匝数比3.166 7，定子额定电压380 V，转子额定电压120 V，定子额定电流4.5 A，转子额定电流10 A，定子漏感0.018 6 H，定子电阻2.659 6 Ω；归算到定子侧的定转子间互感0.298 7 H，转子漏感0.018 6 H，转子电阻5.898 5 Ω。控制器参数如下：r=150，h=0.01;a=0.5，δ=0.01，β1=8 000，β2=6 000；kp1=0.015；kp2=0.000 03，kq1=0.035，kq2=0.000 03。

DFIG并网运行时，一开始有功和无功功率给定为零。0.6 s时刻给定系统-1 000 W（“-”为产生有功功率，吸收无功功率）的有功功率阶跃信号，进行传统DPC和基于非线性观测器的DPC的仿真对比，仿真结果如图4所示。图5为0.6 s时刻给定系统1 000 Var的无功功率阶跃信号的仿真结果。

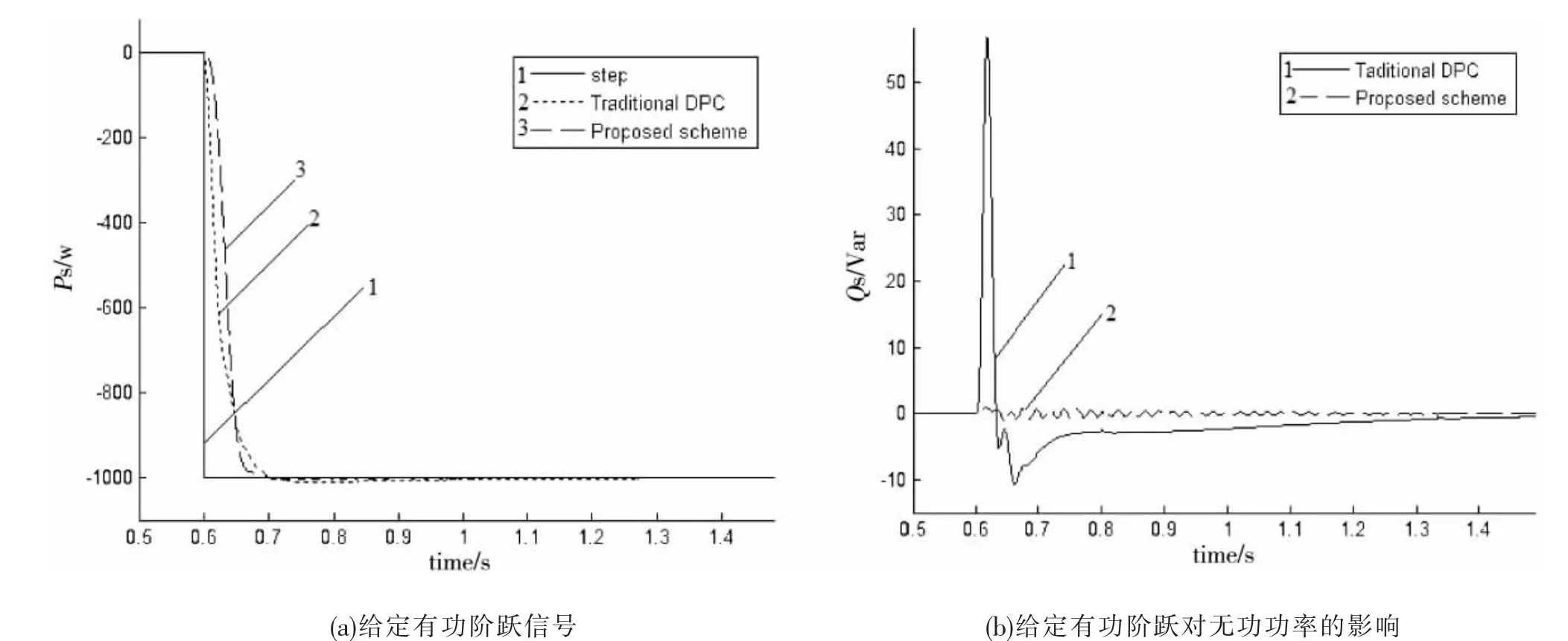
图4 给定有功功率阶跃信号的仿真对比

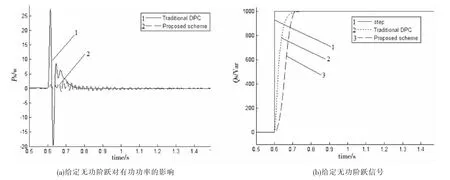
图5 给定无功功率阶跃信号的仿真对比

从图 4（a）和图 4（b）可见，在跟踪有功功率阶跃信号速度相同的条件下，相比传统DPC，基于非线性观测器的DPC较大地削弱了对无功功率的影响。 由图 5（a）和图 5（b）中可见，跟踪无功功率阶跃信号速度相同的情况下，基于非线性观测器的DPC给有功功率带来的影响远小于传统DPC。由此可见，基于非线性观测器的DPC能够基本消除有功和无功功率突变造成相互间的影响。

传统DPC存在超调量与快速性之间的矛盾，而基于非线性观测器的DPC较好地解决了此问题，仿真结果如图6所示。

图6 中step为给定有功功率阶跃信号,Traditional DPC slow为传统DPC超调量较小时的跟踪波形,Traditional DPC fast为传统DPC快速响应时的跟踪波形,Proposed scheme为本文所提出方法的波形。由图6a可见,传统DPC很难做到快速无超调控制，基于非线性观测器的DPC能够实现。由图6（b）可见，在有功功率无超调的情况下基于非线性观测器的DPC定子电流上升速度快于传统DPC，体现更好的动态性能。

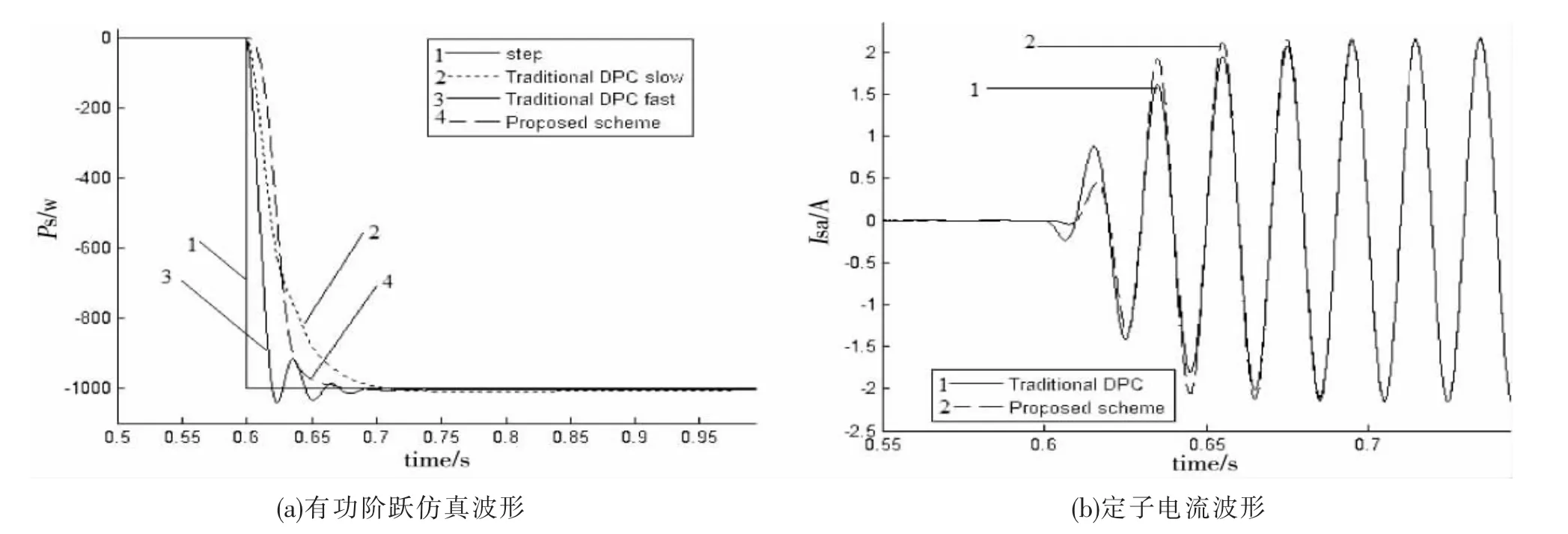
图6 传统DPC与本文提出方法的动态性能对比

4 结论

本文详细论述了基于非线性观测器的DPC思想及实现，该控制策略结构简单且具有较好的动态性能。对传统直接功率控制和基于非线性观测器的DFIG直接功率控制进行了仿真对比研究,结果表明,本文提出的控制方案实现了快速无超调的控制效果，同时减小动态过程中有功功率和无功功率的相互影响。

[1]Si Zhe Chen,N C Cheung,K C Wong,Jie Wu.Integral Sliding-Mode Direct Torque Control of Doubly-fed Induction Generators Under Unbalanced Grid Voltage.IEEE Transactions on Energy Conversion,2010,25(2):356-368.

[2] 贺益康,郑康,潘再平,等.交流励磁变速恒频风力发电系统运行研究[J].电力系统自动化,2004,28(13):55-68.

[3] Tapia A,Tapia G,Ostolaza J X,et al.Modeling and Control of a Wind Turbine Driven Doubly Fed Induction Generator[J].IEEE Transactions on Energy Conversion,2003,18(2):194-204.

[4]Pena R,Clare J C,Asher G M.Doubly fed induction generator using back-to-back PWM converters and its application to variable-speed wind-energy generation[J].IEE Proceedings on Electric Power Applications,1996,143(3):231-241.

[5] 李辉,杨顺昌,廖勇.并网双馈发电机电网电压定向励磁控制的研究[J].中国电机工程学报,2003,23(8):159-162.

[6] Muller S,Deicke M,Doncker R W D.Doubly fed induction generator systems for wind turbines[J].IEEE Industry Applications Magazine,2002,17(1):26-33.

[7]Arnalte S,J C Burgos,Rodríguez-Amenedo J L.Direct torque control of a doubly fed induction generator for variable speed wind turbines[J].Electric Power Components and Systems,2002,30(2):199-216.

[8] 马小亮,刘志强.双馈电动机直接转矩控制技术的研究[J].电工技术学报,2003,18(5):63-68.

[9]Buja G S,Kazmierkowski M P.Direct torque control of PWM inverter-fed AC motors-a survey[J].IEEE Transactions on Industrial Electronics,2004,51(4):744-757.

[10] Xu L,Cartwright P.Direct Active and Reactive Power Control of DFIG for Wind Energy Generation[J].IEEE Transactions on Energy Conversion,2006,21(3):750-758.

[11] Zhi D,Xu L.Direct Power Control of DFIG with Constant Switching Frequency and Improved Transient Performance[J].IEEE Transactions on Energy Conversion,2007,22(1):110-118.

[12] 郭晓明,贺益康,何奔腾.双馈异步风力发电机开关频率恒定的直接功率控制 [J].电力系统自动化,2008,32(1):61-65.

[13] 陈思哲.双馈感应风力发电机组的控制研究 [D].广州:华南理工大学,2010.

[14] 韩京清,王伟.非线性跟踪-微分器[J].系统科学与数学,1994,14(2):177-183.

[15] 韩京清.非线性PID控制器[J].自动化学报,1994,20(4):487-490.

[16] 韩京清.自抗扰控制器及其应用 [J].控制与决策,1998,13(1):19-23.