航天继电器多余物微粒碰撞噪声检测的 冲击试验条件

王淑娟 王国涛 翟国富 张 辉

（哈尔滨工业大学军用电器研究所 哈尔滨 150001）

1 引言

航天继电器广泛应用在航空、航天、军事、现代工业等领域中，在信号控制、传递、处理和交换等方面起到至关重要的作用[1-3]。主要用于导弹、运载火箭、人造卫星、宇宙飞船、航天飞机及其配套地面测控设备中完成信号传递、执行控制、系统配电等功能，是国防电子系统中主要电子元器件之一。

航天继电器的可靠性直接影响着整个国防电子系统的可靠性。在航天继电器生产制造过程中，可能把一些金属屑、焊锡渣、松香、棉丝腊线头、密封剂等多余物（微小微粒）封装在内而附着在继电器内部构件表面上。在航天器工作过程中，由于强烈的冲击或振动使多余物微粒激活，在继电器内部随机游动、碰撞，可能导致航天继电器发生误动作，甚至造成航天事故[4-6]。所以，研究航天继电器的多余物检测技术及相应的预防措施，对于保证整个国防电子系统的可靠性具有重要的理论意义和实用价值。

微粒碰撞噪声检测（Particle Impact Noise Detection，PIND）试验是一种检测航天继电器内部多余物的有效方法，已经被国军标 GJB65B、GJB2888−97 等规定为航天继电器出厂前的必做试验[7-8]。其原理是：由PIND 的振动台产生一系列指定的机械冲击和振动，通过冲击使被束缚的微粒松动，再通过一定频率的振动，使微粒同腔体内壁撞击，将撞击产生的能量以声音和电压波形的形式输出。美国军用规范规定，PIND 检测设备要使用一台最低频率响应为 500kHz、视觉显示灵敏度为20mV/cm 的示波器和一套带有扬声器的，用于监视来自微粒碰撞噪声检测电子线路音频信号的声频系统，规定在PIND 试验中使用正弦振动试验条件与冲击试验条件，正弦振动规定了三个频率：27Hz、40Hz、100Hz，冲击试验条件加速度规定为（200± 40）g，在整个试验过程中加速度恒定，g 是重力加速度[9]。检测系统如图1 所示。

图1 美军规范规定的微粒碰撞噪声检测系统 Fig.1 The PIND system of MIL-R-883E

在PIND 试验中，多余物微粒可能由于机械原因卡住或因静电吸附等原因不能自由游动，从而在振动试验中无法与腔体内壁碰撞发声而导致检测失败。因此，PIND 试验总是要进行多次冲击，冲击试验条件施加的好坏决定了 PIND 试验的成功与否。文献[10-12]通过建立PIND 试验过程的动力学模型研究了振动试验条件下微粒碰撞的一些规律。但是目前对于冲击试验条件的研究鲜有报道。为研究PIND 试验中冲击试验条件的实现过程，精确获得冲击加速度峰值和脉冲持续时间，需要对冲击过程的动力学机理进行分析，找出影响冲击加速度峰值和脉冲持续时间的关键因素；研究冲击试验条件对多余物微粒的分离效果有助于提高试验条件的有效性和针对性，增加PIND 检测的成功率。本文正是在这种背景下展开研究的。

2 PIND 冲击过程的动力学分析

我国及其他国家对航天继电器施加的冲击试验标准中，均规定了冲击脉冲的波形、容差带和相应的速度变化量及容差。其中，半正弦脉冲和后峰锯齿波脉冲是最常使用的冲击波形[7-8]。根据冲击波形物理实现方法的不同，冲击机可以分为自由跌落式冲击机和非自由跌落式冲击机。对于自由跌落式冲击机，其原理是通过一定方式使工作台提升到一定高度，然后突然释放，工作台撞击铁砧上的缓冲器产生冲击，不同类型的缓冲器可以产生各种形状的冲击脉冲。现有的PIND 仪大都是由美国PTI 公司生产的，Model 4501 型PIND 仪是国内应用较多的PIND 检测装置，Model 4501 及哈尔滨工业大学军用电器研究所自行研制的微粒碰撞噪声多余物自动检测系统均使用同样的振动台系统，图2 是其结构图。在冲击开始前，电枢被提到一定的高度（可能具有初速度），之后受电磁力作用向下加速运动，电磁力撤销后电枢在重力的作用继续向下运动，最后与铁砧上的缓冲器发生撞击产生冲击，由于缓冲器的制动作用，使电枢产生向上的冲击加速度，因而属于非自由跌落式冲击。

图2 Model 4501 型PIND 仪振动台结构图 Fig.2 Shaker assembly of model 4501

2.1 动力学分析

将缓冲器看成是有阻尼的线性弹簧，冲击过程可以等效为单自由度线性质量－弹簧系统，如图3所示。图3 中M 为电枢的质量，C 为缓冲器阻尼系数，K 为缓冲器的刚度。

图3 等效的质量-弹簧系统 Fig.3 The model of the ball and space relay cavity

设定向上为正方向，x 代表电枢的位移，电枢与缓冲器刚刚接触时刻为 t=0、x=0，初速度，G 为重力，则其运动方程为

变换后，可以写成

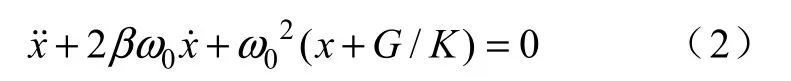
通常使用的缓冲器为橡胶材料，尽管其内摩擦比金属弹簧大1000 倍以上，但阻尼很小，因此，。式（2）简化为

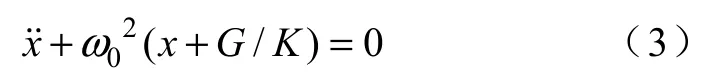
解这个方程，其通解为

对式（4）进行一次、二次微分，得到速度、加速度

由初始条件以及式（5）、式（6），可得

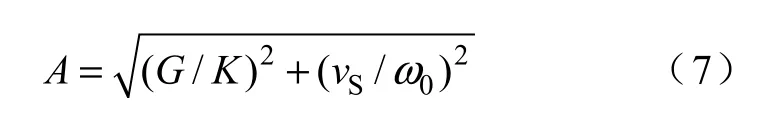
实际情况中00ϕ ≈ °，由式（6）可得冲击加速度 ( )a t 为

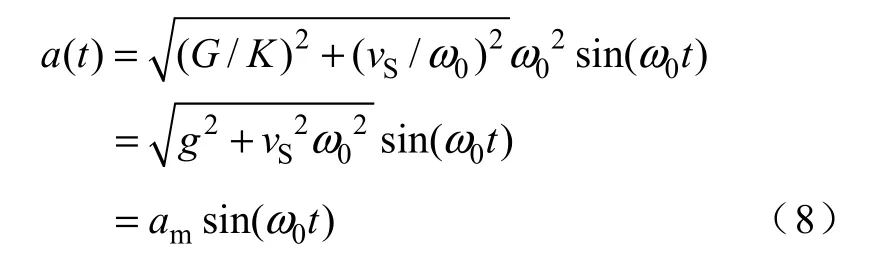
式中ma ——冲击加速度幅值；

g——重力加速度。

在实际使用中，冲击加速度应远大于重力加速度，可得

冲击加速度的周期为

冲击脉宽st 为电枢与缓冲器碰撞的半个周期

式（9）、式（11）表明，冲击加速度为半正弦脉冲，冲击加速度的峰值由初速度及系统固有频率决定，冲击脉宽由系统固有频率决定。图4 为冲击过程中加速度的波形。

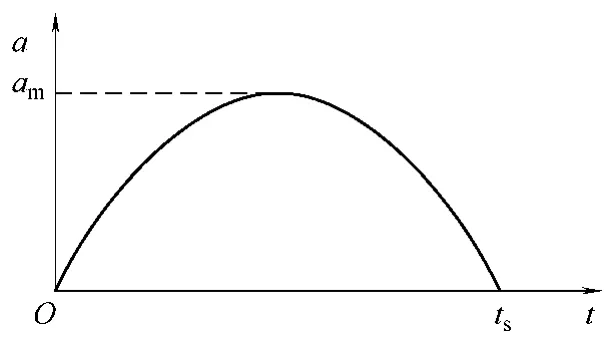
图4 冲击加速度的半正弦波 Fig.4 The waveform of half sine impact

2.2 恢复系数对加速度的影响

在上面的分析中，并没有考虑冲击过程中的能量损失，设e 为电枢与铁砧缓冲器的恢复系数，则电枢与缓冲器的碰撞后速度v 为

在碰撞过程中，根据冲量定理

考虑式（12）、式（13），可得

由于实际振动台电枢与铁砧缓冲器的硬度都很大，恢复系数接近1，在实际应用中经常取恢复系数为1，这时式（14）与式（9）结果一致，式（14）考虑了冲击过程中能量的损失。

2.3 系统参数对冲击加速度的影响

方程（14）表明，冲击加速度的幅值由系统的固有频率、材料特性及电枢初速度决定。非线性恢复力系数δ 的增加意味着缓冲器的硬度变大，冲击加速度的峰值变大，冲击脉宽变小。在实际应用中，通常以冲击加速度的峰值与冲击脉宽的乘积来衡量冲击强度。随着δ 的增加，冲击强度是增加的。随着刚度K 的增加，冲击加速度的峰值变大，冲击脉宽变小，冲击强度增加。

随着Sv 的增加，冲击加速度的峰值变大，冲击脉宽不变，冲击强度增加。当缓冲器材料确定以后，电枢初速度是影响冲击加速度峰值的关键因素。

3 最小冲击加速度与多余物特征参数的关系

微小多余物微粒吸附在腔体内部结构上的主要原因是静电。静电是由原子外层的电子受到各种外力的影响发生转移，分别形成正负离子造成的。任何两种不同材质的物体接触后都会发生电荷的转移和积累，形成静电。多余物微粒与航天继电器腔体壁碰撞时，由于摩擦也会产生静电，对于非导体的多余物微粒，静电会迅速达到饱和，使得静电作用增强，导致多余物微粒吸附在腔体内部结构上。

研究表明：当多余物尺寸小于100μm 时，静电力会远大于重力。在PIND 试验过程中，不存在外电场，此时静电力主要是电像力[13]。带电体的电荷与自身形成的电场之间，也会产生相互作用。这种电荷与因自身电荷感应产生的像电荷间的作用力，称为电像力。电荷q 发出的电通量将终止于包含q的空间导体表面处产生的感应面电荷上，电荷q 与该面电荷之间以库仑力相互作用，与正、负电荷间的库仑力相同，电像力是与距离平方成反比的近距力。

将多余物微粒视为半径为r、密度sρ 、电导率κ 、电荷密度χ 的小球，当其因电像力EF 附着于继电器腔体壁时，由电荷守恒定理

由欧姆定律，有

由高斯定理，有

联立式（15）、式（16）及式（17），得到

积分得到

式中，0ρ 为t=0 时的电荷密度，单位为C/m3；τ 为电荷驰豫的时间常数， /τ ε κ= ，单位为s。

吸附时间t 有最大值ft ，ft 为静电达到饱和所需时间。由式（19）可知，吸附发生后t 时，小球的电荷q 为

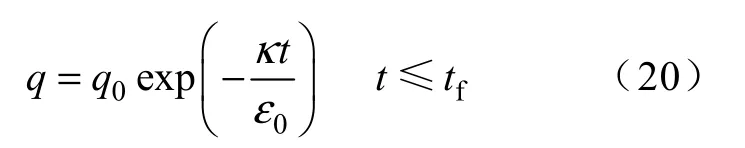
于是电像力EF 为

小球的质量m 为

图5 为微粒的受力图，EF 为电像力，SF 为冲击力，x 为微粒中心与腔体壁的距离，方向以向下为正。在冲击试验条件作用下，小球受到的冲击加速度峰值为Sma ，最大冲击力为SmF ，则有

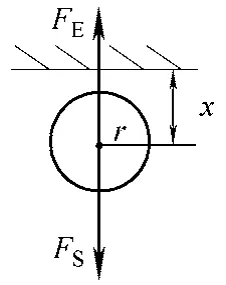
图5 微粒的受力分析 Fig.5 Analysis of particle under stress

为使多余物与腔体壁分离，冲击力应大于电像力，即应有SmF ＞EF ，考虑式（21）及式（22），可得

若小球为绝缘体，则

在整个分离过程中，应有

式中，a 为微粒的加速度。

冲击力SF 可表示为，可以得到

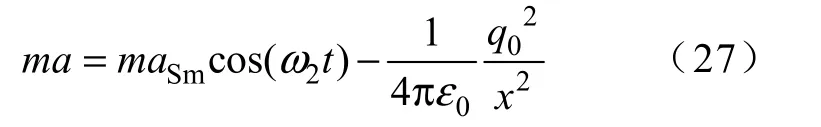
即为冲击过程中多余物微粒的运动方程。

最小冲击加速度尽管可以使多余物微粒活动，但不一定能使微粒与腔体壁完全的分离。通常冲击脉冲为半正弦脉冲，按半正弦曲线变化，而电像力与分离距离的二次方成反比。在整个分离过程中，冲击加速度与电像力所产生的加速度均减小，若冲击加速度始终大于电像力加速度则分离可以进行完全，即多余物微粒被激活，反之，激活过程并不完全。

综上可知，多余物微粒能否激活是由冲击加速度峰值和冲击脉宽共同决定的，二者作用同样重要。

4 冲击试验条件的确定原则

由上文可知，冲击加速度峰值越大对多余物微粒激活效果越好，但是显而易见，冲击对被测器件的破坏作用也同时增大。PIND 试验是一种非破坏性的试验，冲击试验条件不应破坏被试继电器的物理特性及电特性。本部分研究以现行国军标为基准，确保冲击试验条件对被试件的破坏作用不大于现行国军标的前提下，增加冲击试验条件的加速度峰值以提高冲击试验条件对多余物微粒的激活效果，提高PIND 试验的检测精度。

被试器件在冲击过程中的应力是导致其损坏的直接因素，要以现行国军标为基准调整冲击试验条件，应保证被试器件在不同冲击试验条件下所受的应力相等，因此，应选择“损伤等效原则”作为调整冲击条件的准则。

“损伤等效原则”具体为：若被试件的固有频率为fn，受到脉冲峰值加速度为A1、脉冲持续时间为T1的半正弦波脉冲的冲击，amax1为其加速度最大响应值；改变后的冲击脉冲峰值加速度为A2，持续时间为T2，amax2为其加速度最大响应值。若下式成立则两者损伤效果相当

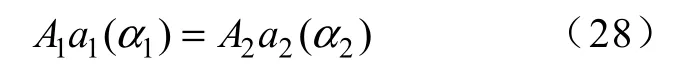
式中，α1、α2为相应于T1、T2的归一化频率（α= fnT）；a1(α1)、a2(α2)为相应于T1、T2的归一化响应系数，a1(α1) = amax1/A1，a2(α2) = amax2/A2，其数值可以从IEC68 标准和相应国家标准的冲击试验方法给出的对称半正弦脉冲的冲击响应谱中查找得出[14]。

为了更好地说明，现将GJB 360A 方法213 的试验条件A、B、C 与PIND 试验的两种冲击条件列于表1 中，并计算其损伤度。对于有可靠性指标要求的航天继电器，一般其固有频率都很高，本计算中继电器固有频率取2000Hz。

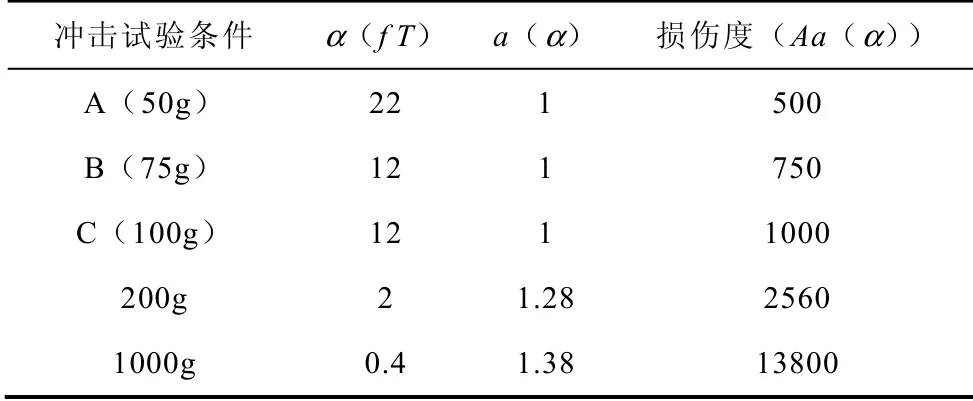
表1 损伤等效原则 Tab.1 Equivalent damage principle

表1 表明，5 种冲击试验条件的损伤效果依次增加，按照冲击加速度峰值的大小递增排列。考虑表1 最后两行，冲击加速度峰值200g、冲击脉宽1ms是GJB 65B−99 附录B 的现行规定，以此为基准应用“损伤等效原则”：将冲击加速度峰值设定为1000g，则其归一化响应系数a=2560/1000g=0.256，查表得到其归一化频率为α = 0.11，则冲击脉宽为0.11/2000=55μs，即冲击加速度峰值为1000g、冲击脉宽55 μs 的冲击试验条件与GJB 65−B 附录B 的冲击试验条件对被试继电器的损伤可以认为是相当的。

表2 给出了改变冲击加速度峰值后的一些“损伤等效”的冲击试验条件，可以看到，随着冲击加速度峰值的增加，冲击脉宽很快减小。

表2 损伤等效原则确定的冲击试验条件 Tab.2 Impact test conditions by equivalent damage principle

5 实验验证

取某型号的航天继电器4 只，其中2 只放入铅锡混合微粒（焊料），质量分别为0.01mg、0.12mg，标记为R1、R2。另外2 只放入橡胶微粒，质量分别为0.02mg、0.16mg，标记为R3、R4。采用哈尔滨工业大学军用电器研究所自行研制的微粒碰撞噪声多余物自动检测系统进行PIND 试验。为减小各次试验间相互干扰，同一继电器相邻两次试验时间间隔至少为10min。考虑到市面上PIND 用振动台冲击脉宽多为1000μs、100μs，所以制定实验方案如下：①使用冲击时间1000μs 的振动台，采用GJB 65B−99 附录B 的试验条件进行试验，标记为C1，每只继电器试验30 次；②使用冲击时间100μs 的振动台，冲击加速度峰值400g，其他条件按照GJB 65B−99 附录B 的规定进行试验，标记为C2；每只继电器试验30 次。实验结果如下：

表3 列出了两种PIND 试验方案的检测结果。使用方案C1 时，R1、R2、R3、R4 的多余物检出次数分别为20、27、19、26，总检出次数为92，检出比率分别为 66.7%、90.0%、63.3%、86.7%。使用方案C2 时，R1、R2、R3、R4 的多余物检出次数分别为27、23、25、21，总检出次数为96，检出比率分别为90.0%、76.7%、83.3%、70.0%。

表3 PIND 试验结果 Tab.3 Experimental results

由实验结果可见，冲击加速度峰值的提高可以提高PIND 试验的检测精度，并且可以更有效地激活微小多余物，从而提高PIND 试验的检测精度。但对于较大的多余物则不能有效激活，检测精度略有下降，此时应选用较小的冲击加速度峰值条件（较大的冲击脉宽）。这一结果同加速度峰值越大激活效果越好的理论预测有偏差，分析原因如下：

（1）理论预测是对理想条件下即理想空腔中多余物检测进行分析，而实际继电器内部环境并非理想空腔，其内部存在线圈、衔铁、触点等各种组件，差异很大。

（2）PIND 检测本身存在一定随机性，影响多余物的检测精度的因素除了多余物微粒激活效果外，还有振动试验条件、被测器件内部结构、检测时的各种噪声干扰等其他影响因素。

另外，冲击加速度峰值的提高对金属多余物微粒的检测效果提升相对更加明显；冲击脉宽的增大对非金属多余物微粒的检测效果提升更加明显。

现行多余物检测的难点和重点是微小质量多余物检测和金属多余物检测，因此，在实际选用冲击试验条件时，可以使用多种冲击试验条件以最大限度地激活多余物。

6 结论

（1）本文建立了PIND 冲击过程的数学模型，分析了冲击加速度半正弦波的形成机理，推导了冲击加速度幅值与冲击脉宽的表达式，并分析了能量损失情况及系统参数对冲击加速度的影响。

（2）基于电像力理论分析了多余物微粒的吸附现象，推导了最小冲击加速度与多余物微粒物特征参数的关系，指出多余物微粒能否激活是由冲击加速度峰值和冲击脉宽共同决定的。

（3）根据“损伤等效原则”调整冲击试验条件，在原GJB 65B−99 的PIND 冲击条件基础上，给出了等效的冲击条件表。

（4）实验结果表明选择不同的冲击条件，可以实现对不同大小的多余物微粒进行有效的激活。冲击加速度峰值的提高可以提高PIND 试验的检测精度，并且可以更有效地激活微小多余物，从而提高PIND 试验的检测精度。

[1] Ding Maosheng,Wang Gang,Li Xiaohua.Reliability analysis of digital relay[C].8th IEE International Conference on Developments in Power System Protection,The Netherlands,2004,1:268-271.

[2] Roettjer P.Testing techniques to improve relay reliability[J].EE:Evaluation Engineering,2005,44(4):44-48.

[3] Ishikawa K,Miki T,Mamiya H,et al.Early-stage analysis for MEMS structural optimization II:its application to microrelay reliability[C].Proceedings of the ASME/Pacific Rim Technical Conference and Exhibition on Integration and Packaging of MEMS,NEMS,and Electronic Systems:Advances in Electronic Packaging,2005,Part C:1631-1636.

[4] 郑南昌.控制系统继电器可靠性分析与措施[J].火箭推进,2005,31(4):58-62.

Zheng Nanchang.Reliability analysis and counter- measures of relays in the control system[J].Journal of Rocket Propulsion,2005,31(4):58-62.

[5] 李大南.航天型号产品多余物及其预防和控制标准的实施检查[J].航天标准化,2006(1):17-20.

Li Danan.The implementation inspects of space product superabundance and its prevent and standards[J].Astronautics standardization 2006(1):17-20.

[6] Hammerstrom I,Kuhn M,Wittneben A.Channel adaptive scheduling for cooperative relay networks[C].2004 IEEE 60th Vehicular Technology Conference,2004,60(4):2784-2788.

[7] GJB 65B−1999.有可靠性指标的电磁继电器总规 范[S].

[8] GJB 2888−1997.有可靠性指标的功率型电磁继电器总规范[S].

[9] MIL-STD-883E 2020.7,Particle Impact Noise Detection Test[S].

[10] Zhang H,Wang S J,Zhai G F.Dynamic model of particle impact noise detection[C].IEEE IECON,2004:2577-2581.

[11] Zhang H,Wang S J,Zhai G F.Test conditions discussion of particle impact noise detection for space relay[C].IEEE IECON,2004:2566-2572.

[12] 张辉,王淑娟,翟国富.航天继电器多余物微粒碰撞噪声检测的单周期稳定性分析[J].航空学报,2005,26(3):362-366.

Zhang H,Wang S J,Zhai G F.One-period stability analysis of particle impact noise detection for space relay reminders[J].Acta Aeronautica ET Astronautica Sinica,2005，26(3) :362-366.

[13] 鲍重光.静电技术原理[M].北京:北京理工大学出版社,1993.

[14] 汪凤泉.电子设备振动与冲击手册[M].北京:科学出版社,1998.