基于稳定性CICC 设计模型
蒋华伟 李国平 赵玉娟 武松涛
(1.河南工业大学信息学院 郑州 450001 2.中国科学院等离子体物理研究所 合肥 230031)
1 引言
CICC(管内电缆导体)是在Hoenig 等人提出的内冷超导体(ICSs)和 CIC 概念基础上演变而 来[1]。经过多年研究、发展和改进的CICC 因具有良好冷却、高电压绝缘、大电流、低损耗、多级变位股绞缆等优点而为中国大科学工程EAST、韩国KSTAR 以及国际热核聚变试验反应堆ITER[2]等超导磁体的首选导体。
CICC 的结构决定其间的热交换是一个复杂的过程,加上CICC 运行在大电流和快变磁场中,其稳定性还受到能量裕度和AC 损耗等的制约,这使得工程上CICC 的绞缆成为一个精细复杂、多次尝试和改进、工作量巨大的烦琐过程。如果采用数值仿真设计,则会使工作量相应地减轻,周期缩短。
目前针对CICC 所开展的数值模拟研究工作主要集中在稳定性、损耗等方面。其中关于CICC 导体稳定性工作,如文献[3]针对热传导和沿导体长度方向上的失超传播等问题,提出数值分析方法。文献[4]中提出子缆包绕及中心冷却的CICC 导体3D绞缆数值模拟模型,它可以输出股线的空间结构、每级子缆的面积等。文献[5]针对KSTAR 上的导体,探索了瞬时热传递和暂态温度裕度补偿特性;在给定运行条件下,对能量裕度、质量流分布及CICC中氦流对入口位置、压力等质量流衰减和温升峰值的依赖性进行研究。
在导体损耗方面进行的研究工作有:文献[6]对NbTi 超导CICC 的AC 损耗与股线内接触电阻进行了研究,获得AC 损耗和接触电阻的对应关系。文献[7]使用实验分析的方法,研究了处于交变脉冲环境中多股绞制的超导电缆的电磁问题,用数值方法评价了AC 损耗。另外在文献[8]中提出一种通过调节导体中子缆纽绞方向和节距的方法,来解决导体不能同时获得低损耗和高稳定性的难题。
这些研究多基于理论实验方法获得CICC 的稳定性与磁场、电流密度、温度和质量流等的关系,以及寻找CICC 导体结构对AC 损耗影响的因素,为 CICC 的稳定性运行作了大量有意义的探索工作。但没有涉及基于给定运行条件对CICC 导体结构进行设计研究,虽然文献[3]中L.Bottura 等进行了导体数值分析,但主要是对CICC 的失超传播进行模拟,不是导体结构的数值模拟设计。为此,本文在上述研究工作基础上,提出了基于稳定性、质量流和AC 损耗机理的CICC 结构设计数值仿真模型,并尝试完成导体结构的模拟设计研究。
2 CICC 数值模拟理论
2.1 CICC 稳定性裕度
运行在复杂变化电磁场环境中的 CICC,其稳定性不仅受运行条件、空隙率、子缆的扭距、股线及子缆结构等影响,而且受液氦流速和质量流的约束,另外CICC 的稳定性还与铜超比和股线表面镀层(高阻层)等密切相关。因此,对CICC 稳定性的研究是导体设计的核心和关键。
由于CICC 的稳定性是受某一温度范围内液氦焓差的限制,这样可对该温度区间内液氦的热容进行积分得到焓差的值。数学描述如下:
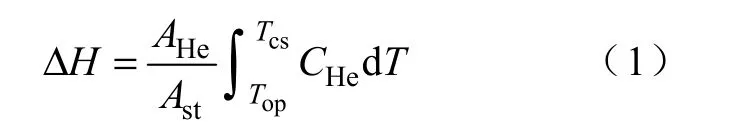
式中,AHe和Ast是液氦和超导体的面积;Tcs、Top是分流温度和运行温度;CHe是液氦的热容。
根据能量平衡并结合在整个干扰区间内液氦和股线的情况,可以粗略地估计出在好冷却区间、过渡区间和差冷却区间的稳定性裕度。
在好冷却区,运行电流小于下极限电流,温度能够上升到分流温度,由于液氦的热容远大于超导股线的(超导股线的贡献可忽略不计,近似为零),可用的最大液氦热沉为
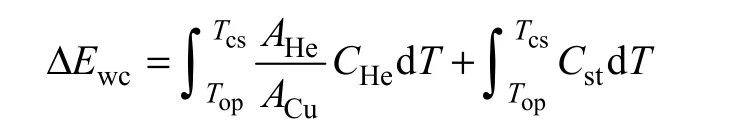

式中,ACu是铜的面积;Cst是超导股线的热容。
在过渡区间,运行电流处在下、上极限电流之间,液氦的温度仅可以上升到恢复温度Trec。
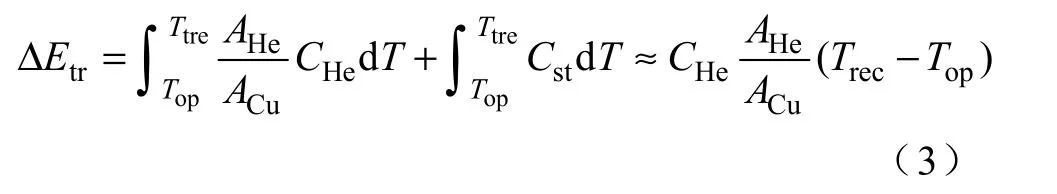
在差冷却区间,运行电流大于上极限电流,没有可利用的液氦焓差,由于超导股线的热容非常小,导体可利用的焓差近似为零,所以有

2.2 CICC 稳定与质量流
在对ITER 的导体进行实验研究和分析时,发现液氦的有用焓值(稳定性)与质量流的关系如图1 所示(内部温度:4.5K,最大输出温度:6K),这说明了CICC 导体的稳定性与质量流之间存在一定的相关性。
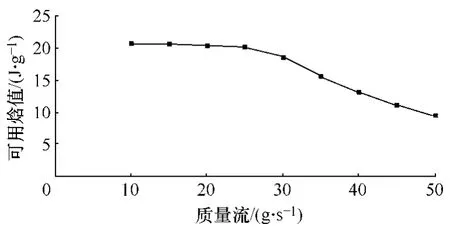
图1 焓值与质量流的关系 Fig.1 Relationship between enthalpy and mass flow rate
实际中稳定性与质量流关系的资料是通过试验等提供的曲线图,由这些图不仅得不出CICC 稳定性与氦流量之间的准确关系,甚至也难以获得曲线上每一点真正对应的数据,用程序进行导体稳定性研究及导体结构数值模拟设计时,由于不知道稳定性裕度和质量流之间的确定关系,就无法进行精确的计算,因此需要对它们进行量化,用数学表达式来描述它们之间的定量关系。
为此采用图像处理和最小二乘法相结合的方法来量化它们之间的关系[9]。首先对图像进行处理,然后利用最小二乘法对二值化的图像曲线进行拟合,最后获得CICC 稳定性裕度与迫流氦流量之间的量化关系,这样就可以为后面的CICC 数值模拟设计提供经验计算模型。
3 CICC 结构数值仿真设计模型
3.1 CICC 设计的基本思路
由三根超导股线构成的一级子缆的情况,已经进行过数值仿真研究[10]。本次的情况是给定运行电流、温度、背景场及预定的稳定性裕度、温度裕度、导体的空隙率等参数,但不知是否含有纯铜股线。其设计的基本思路是:在给定运行条件下,根据空隙率、稳定性裕度、温度裕度等,结合stekly 参数小于1 的情况,利用导体中铜的面积和湿边周长(考虑稳定性裕度)和电缆空间电流密度(优化铜组分),以及超导材料的临界电流密度(温度裕度),获得关于超导股线根数、超导股线直径和铜超比等参数的矩阵方程,由此模拟获得CICC 导体结构。
在构造仿真计算模型中采用了以下假定条件:
(1)一级子缆采用3 根股线绞缆(可以包括铜股线;一般全为超导股,通过铜超比来调节)。
(2)为获得合理的电流密度,给定导体运行在过渡区间,即运行电流大于下极限电流小于上极限电流。并设定stekly 参数小于1,即导体产生的焦耳热小于被液氦带走的能量。
(3)若有纯铜股线则可处理成三种情况:在计算起稳定作用的铜面积以及湿边周长时都包括纯铜股线的作用;仅在计算起稳定作用的铜面积时考虑铜股线的作用;仅在计算湿边周长时考虑铜股线的作用。在模拟程序中对此分别进行处理。
在绞缆中,模拟程序还对导体进行了如下处理:若子缆间内切圆的直径大于前一级子缆的直径,则用相应的纯铜股线来填充,以增强CICC 导体的结构和运行稳定性。
3.2 导体设计稳定性裕度算法模型
根据导体运行在过渡区[10](Ilim,low<Iop<Ilim,up),由稳定性裕度和stekly 参数 α 可得
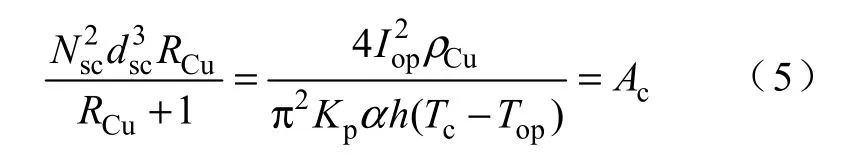
式中,Nsc、dsc分别代表CICC 中超导股线的根数和直径;RCu为铜超比;Iop是运行电流;ρCu为铜的电阻率;Kp是计算湿边周长因子;h 为液氦的热传递系数;Tc是临界温度。
3.3 导体设计空间电流与温度裕度算法模型
根据电缆空间极限电流密度[10],由上极限电流密度与过渡区极限电流密度可得

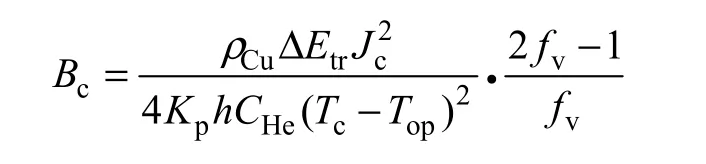
式中 式中,ΔEtr为过渡区的稳定性裕度;Jc表示临界电流密度;fv为导体空隙率。
根据温度裕度和临界电流[10]可以得到
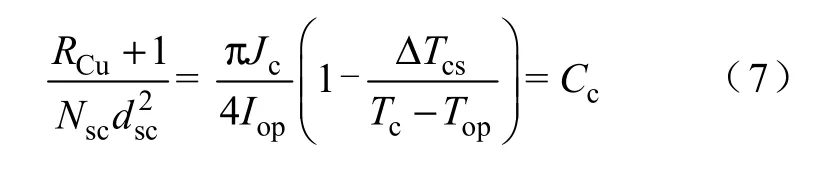
式中,ΔTcs代表CICC 的温度裕度。
3.4 导体数值仿真设计模型
由上面的推导可得式(5)~式(7)三个方程。很显然,上述包含三个未知量Nsc、dsc、RCu的方程是不难求解的。可是,当把式(7)代入到式(5)时会得到类似于式(6)的方程。这说明在空间电流密度上对CICC 铜组分的优化不是孤立的问题,是与稳定性裕度、温度裕度及临界电流有着必然的联系。这样就只剩下两个方程,因此无法唯一确定上面三个未知量。鉴于此,可以把RCu、dsc表示成Nsc的函数,逐步尝试用由一、二、三、四等层的结构来确定超导股数Nsc,再求出符合实际要求的RCu及
dsc。
由式(7)得到RCu表达式为

然后把式(8)代入式(5)得到关于dsc的方程

根据不同的CICC 结构来确定Nsc,结合运行电流和临界温度等条件,来获得合理的股线直径dsc,最后由式(9)求得RCu。
根据上面的数学模型,项目组独立研发了CICC结构设计的模拟程序。在CICC 数值仿真时,对不同结构下的Nsc,调用求解dsc三次方程的子程序计算dsc,并判定合理的股线直径dsc,然后计算出相应的铜超比RCu。模拟运行结果如图2 所示。
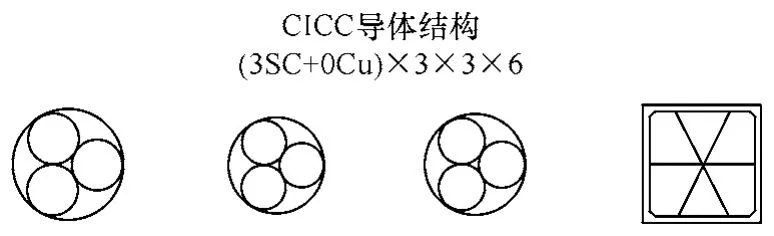
图2 数值仿真得到的CICC 结构 Fig.2 CICC configuration by simulation design
4 CICC 交流损耗
通过上面数值模拟设计所获得的CICC 导体结构,能否满足实际运行条件,还要考虑AC 损耗等因素对稳定性的影响。因为CICC 运行在复杂电磁场和其他恶劣环境中,会产生包括磁滞损耗、耦合损耗和涡流损耗在内的交流损耗[11]扰动,一旦导体的稳定裕度不满足扰动条件,就会产生局部的正常区,若该种趋势得不到遏制就会发生失超传播,最后导致CICC 的整体失超。
CICC 的磁滞损耗可用洛伦兹力做功来表示,对导体所处变化磁场中的磁化曲线进行积分即可。具体由Poynting 矢量S=E×H 对电流或场积分,或由导体的电流密度和电场点积Jc·E 进行积分计算获得,单位体积上纵向磁滞损耗的经验公式为
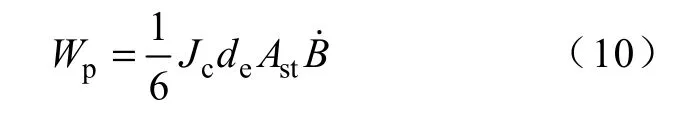
式中,de为超导丝的有效直径;B˙为磁场变化率。
对处于交变磁场中的 CICC,在铜基体中由于产生耦合电流而形成耦合损耗。CICC 是由多股、多级子缆扭绞而成的超导电缆,各级子缆的扭距长度和横向电阻率也存在差异,因此,关键是如何根据这些参数来计算CICC 导体的耦合损耗时间常数和耦合损耗。
当外场的变化速率不大时,计算损耗时可以不考虑屏蔽效应,这样其表达式为
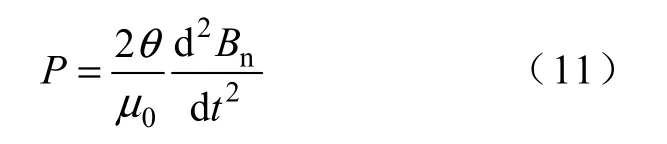
式中,θ 为耦合损耗时间常数;μ0是真空磁导率;Bn为横向磁场的大小。
对线圈励磁、等离子体放电或破灭等极端情况,CICC 的超导细丝大都处于饱和状态,则需考虑饱和系数。因此,耦合损耗功率可采用如下方法。
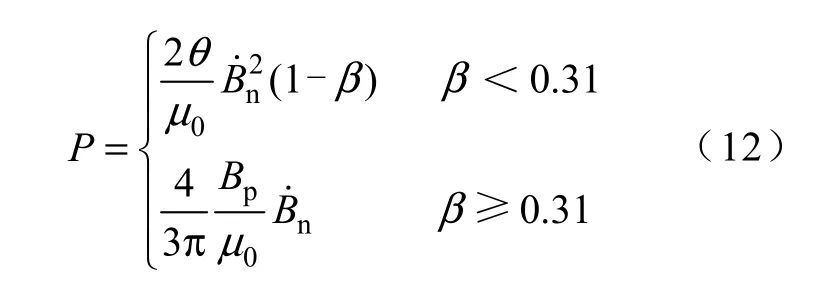
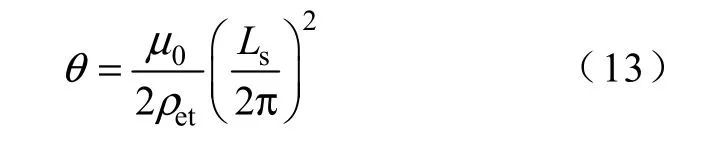
式中,ρet是铜基体中的有效横向电阻率;Ls为股线长度。
对耦合损耗功率在磁场变化时间范围内积分,就可以获得耦合损耗

由耦合损耗和磁滞损耗可获得CICC 在给定运行条件下的交流损耗。经模拟程序计算可以获得数值仿真设计中 CICC 导体耦合损耗时间常数θ 为41.25ms,交流损耗Ec为78.27mJ/cm3(具体比较见表)。
5 结果比较与分析
为了对比数值模拟设计结果,在中科院等离子体所获得了目前国际上正在进展中聚变装置磁体上CICC 导体的最新数据,特别是根据印度SST—1 的CICC 结构制作了导体模型,进行了CICC 导体试验和数据验证。最后从数据库中调出相应运行条件下的模拟设计数据,将其与印度SST—1 的工程设计值比较见下表。
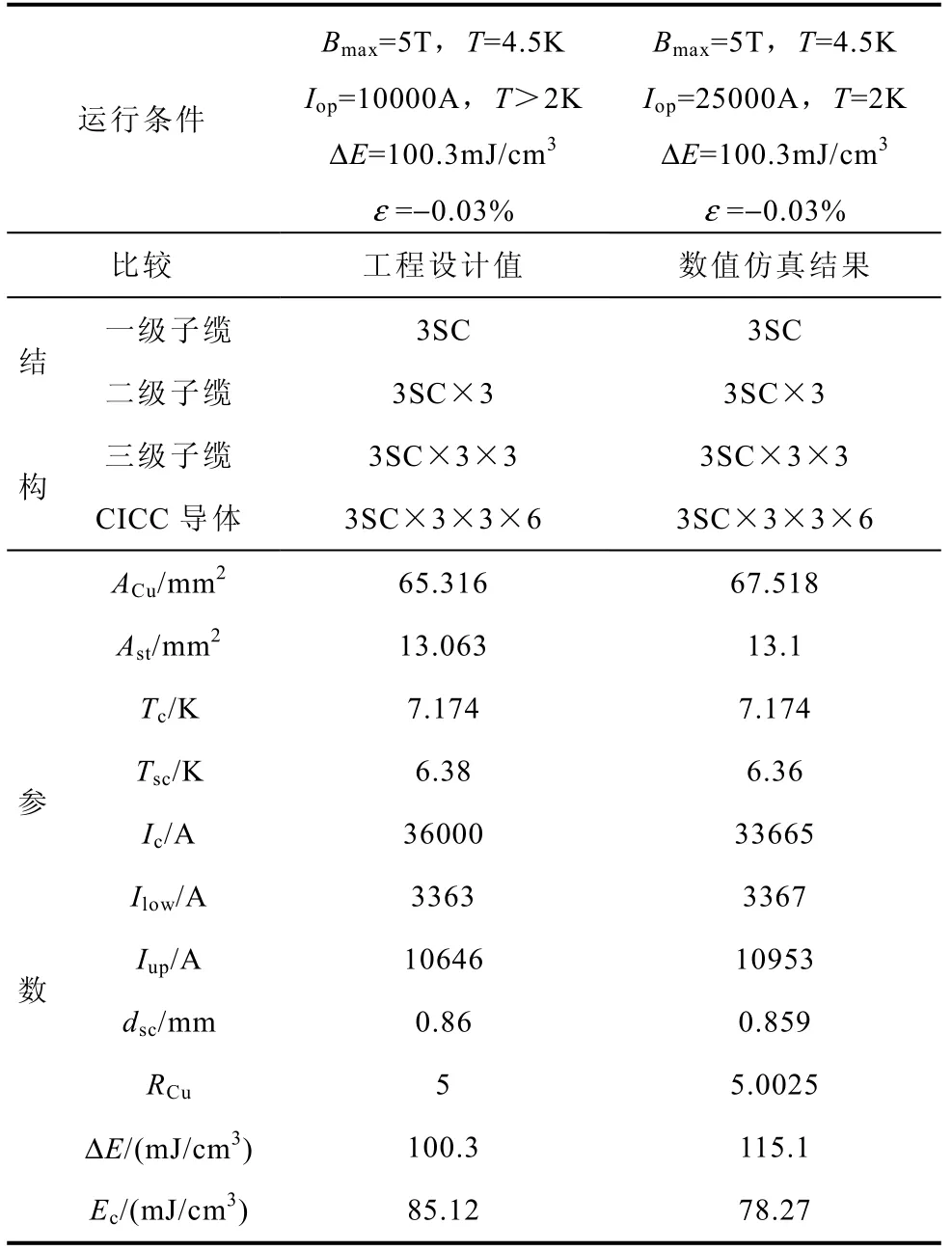
表 数值仿真设计结果与工程设计值比较 Tab. Comparison between simulation results with that of and engineering design
由上表可知,数值仿真给出的CICC 结构与工程设计结果吻合得很好。但在设计参数上存在一定的差异:如在数值仿真中,由于绞缆系数不同导致ACu的不同;Ic的不同主要因为Ic计算方法不同所致(数值仿真采用Ic=AscJc;工程上是由经验给定某一运行条件下单股超导线的临界电流计算而来);稳定性裕度ΔE 不同主要是因为ACu不同;交流损耗的差异主要由耦合损耗时间常数所致。
针对这种问题,在本程序中根据导体一级子缆结构、股线直径以及电缆层(级)数,拟采用合适的湿边周长系数等来弥补计算误差。同时,根据一级子缆结构,并结合参考文献[10]的有关结果,来选取相应的液氦热传递系数加以修正。
由对比分析还可得出:在给定的运行条件下,由程序得到的 CICC 结构,经模拟计算获得损耗Ec=78.27mJ/cm3,小于工程设计值85.12mJ/cm3,说明模拟获得的导体其扰动小于工程设计结果;数值仿真程序所得到的导体稳定性裕度ΔE=115.1mJ/cm3,它大于工程设计值100.3mJ/cm3,说明数值模拟得到导体相对更稳定;同时数值仿真设计中交流损耗小于工程设计和仿真获得的稳定性裕度值,这说明模拟设计的CICC 导体是可以在该条件下较好地稳定运行,因而数值仿真的结果是基本合理和可靠的。
6 结论
本文提出 CICC 结构数值仿真设计的基本思路,并给出一级子缆采用3 根股线、CICC 运行于过渡区间以及纯铜线起不同作用的假定条件,推导和构建了数值仿真设计的算法模型;并对导体的交流损耗进行了理论研究和模拟计算。为工程上快速准确设计导体开辟了新的思路和方法。
通过仿真得出CICC 结构,并对数值仿真设计结果与工程设计值进行了比较,由导体的损耗值不大于稳定性裕度可知CICC 是可稳定运行在给定工况下;另外还分析了模拟设计与工程值产生差异的原因,提出了改进方法。这为磁体系统中CICC 的设计提供了参考。
[1] Dresner Lawrence.Twenty years of cablie-in-conduit conductors,1975-1995[J].Joural of Fusion Enery,1995,14(1):3-11.
[2] Martinez A,Duchateau J L,Tadris L.Transverse heat transfer coefficients on a full size dual channel CICC ITER conductor[J].Cryogenics,2006,46(6):530-540.
[3] Bottura L,Calvi M,Siemko A.Stability analysis of the LHC cables[J].Cryogenics,2006,46(7-8):481- 493.
[4] Qin Jinggang,Wu Yu.A 3D numerical model study for superconducting cable pattern[J]. Fusion Engineering and Design,2010,85(1):109-114.
[5] Qiuliang Wang,Cheon Seong Yoon,Sungkeun Baang,et al.AC losses and heat removal in three-dimensional winding pack of Samsung superconducting test facility under pulsed magnetic field operation[J].Cryogenics,2001,41(4):253-265.
[6] Nijhuis A,Ilyin Yu,Abbas W,et al.Change of interstrand contact resistance and coupling loss in various prototype ITER NbTi conductors with transverse loading in the Twenty Cryogenic cable press up to 40,000 cycles[J].Cryogenics,2004,44(5):319-339.
[7] Kazutaka Seo,Katsuhiko Fukuhara,Mitsuru Hasegawa.Analyses for inter-strand coupling loss in multi-strand superconducting cable with distributed contact resistance between strands[J].Cryogenics,2001,41(2):121-137.
[8] Kawagoe A,Sumiyoshia F,Mitob T,et al.Compact stranded superconducting conductors with both low AC loss and high stability.I.Proposal of a new design[J].Cryogenics,2004,44(9):617-622.
[9] 蒋华伟,张庆州.基于图像曲线和最小二乘法进行函数拟合的研究[J].计算机应用与软件,2007,24(7):43-44.
Jiang Huawei,Zhang Qingzhou.Research on function fitting based on image curve and method of least squares[J].Computer Applications and Software,2007,24(7):43-44.
[10] 蒋华伟,李战升,武松涛.考虑应变的管内电缆导体设计模型[J].西安交通大学学报,2010,44(5):75-79.
Jiang Huawei,Li Zhansheng,Wu Songtao.Simulation model for cable-in-conduit conductor design considering strain effect[J].Journal of Xi’an Jiao Tong University,2010,44( 5):75-79.
[11] 李保增,毕延芳,吴维越,等.大型超导电缆交流损耗的计算[J].低温与超导,2000,28(4):14-18.
Li Baozeng,Bi Yanfang,Wu Weiyue,et al.Calculation of AC losses in large scale supercon- ducting cable[J].Cryogenics and Super Conductivity,2000,28(4):14-18.

