LCL滤波的三相电压型PWM整流器无传感器有源阻尼控制方法

郭希铮 游小杰 李欣然

（1. 北京交通大学 北京 100044 2. 中国北车股份有限公司研究院 北京 100078）

1 引言

电压型PWM整流器（Voltage Source Rectifier，VSR）具有直流电压可控、网侧输入电流畸变率低、高功率因数以及能量双向流动等优点，在光伏并网发电、有源电力滤波器等工业领域得到了广泛的应用[1-2]。

三相电压型PWM整流器输出滤波器采用LCL滤波器要达到相同的滤波效果时，其总电感量比 L滤波器小得多，有利于提高电流动态性能，使中间直流电压的取值更为合理，同时能降低成本，减小装置的体积和重量。在中大功率应用场合，LCL滤波器的优势更为明显。

LCL滤波器存在其物理参数决定的谐振频率，威胁系统的安全运行。为解决此问题，多采用在滤波电容支路串联阻尼电阻的无源阻尼（Passive Damping, PD）方法使系统稳定。这种方法具有简单可靠，不需要改变控制器结构及参数等优点，但是由于阻尼电阻的损耗，造成系统效率降低。

通过改变控制器结构使得系统稳定的“有源阻尼”（Active Damping, AD）技术受到越来越多的关注。Pekik Argo Dahono提出一种“虚拟电阻”的AD控制策略，通过传递函数的变换将真实的阻尼电阻移到控制器内[3]。这种方法具有简明的物理意义，国内也有学者对该方法进行了研究[4]。V. Blasko提出基于超前—滞后模块（Lead-Lag）的滤波电容电压反馈的有源阻尼方法[5]，该方法外加传感器采集滤波电容电压，增加系统成本；M. Malinowski提出一种滤波电容电压观测方法[6-7]，但是其算法中涉及微分运算，难以实际应用。

本文首先采用LCL滤波器三相电压型PWM整流器电流控制策略进行分析，随后对基于超前—滞后模块（Lead-Lag）的滤波电容电压反馈的有源阻尼方法进行分析，分析表明其本质是将滤波电容电压的高频分量引入控制环节。在此基础上，提出一种无传感器有源阻尼控制策略，将电网谐波电压引入控制环节，并采用零阶保持的方法对系统进行离散化，在z域分析了系统的稳定性，仿真结果验证了所提出的有源阻尼控制策略的有效性。

2 LCL滤波器的三相电压型PWM整流器电流控制策略

三相电压型PWM整流器采用LCL滤波器时主电路拓扑结构如图1所示。

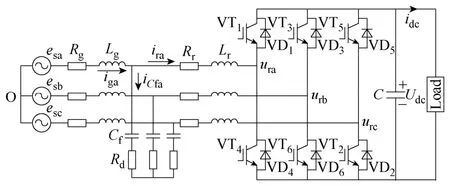
图1 基于LCL滤波器的三相电压型整流器主电路图Fig.1 Power circuit of three-phase voltage source PWM rectifier based on LCL-filter

图中 VT1～VT6为 IGBT，Lg为网侧电感，Lr为整流器侧电感，Cf为滤波电容，Rd是为了避免LCL滤波器在其谐振点出现零阻抗而设置的阻尼电阻，Rg和Rr为电感等效电阻。C为直流侧支撑电容，Udc表示直流侧电压，esx表示各相电网网压，urx表示整流器交流侧输出相电压，irx为整流器侧相电流，igx为网侧相电流，iCfx为电容支路相电流（x=a，b，c），电流参考方向如图1所示。

分析LCL滤波器的三相电压型PWM整流器数学模型时，滤波器的Lg、Cf部分只对高频分量作用，在低频（工频 50Hz）时，LCL滤波器可以建模为LT（LT=Lg+Lr），忽略滤波电容Cf的作用，因此，在以电网电压定向的同步旋转坐标系下，其数学模型为

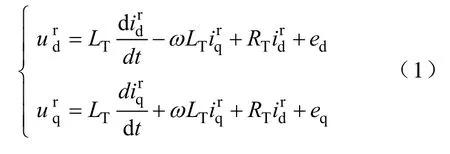
式中，LT=Lr+Lg；RT=Rr+Rg。

根据式（1），控制框图如图2所示，通过前馈解耦的方法抵消由于旋转变换引入的交叉耦合项的影响，当参数准确时，采用PI调节器即可获取理想电流动态调节特性。

图2 LCL滤波器的三相PWM整流器电流控制框图Fig.2 Current control scheme of three phase voltage PWM rectifier with LCL filter

3 LCL滤波器的谐振抑制方法

3.1 LCL滤波器传递函数模型

LCL滤波器的单相等效电路模型如图3a所示，图3b所示为其传递函数模型。

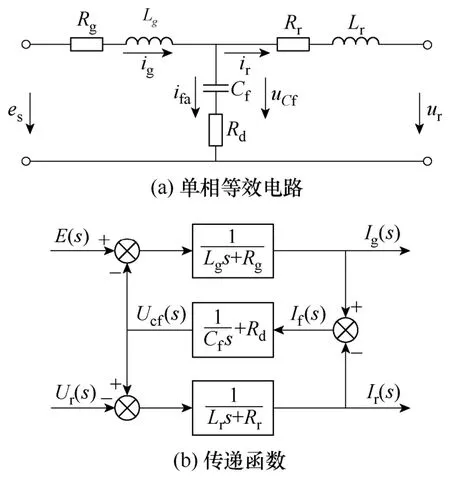
图3 LCL单相等效电路及传递函数Fig.3 Single-phase equivalent model and transfer function of LCL filter

以 Ir（s）、Ig（s）、UrCf（s）为状态变量，E（s）和Ur（s）为输入变量的系统状态方程如下

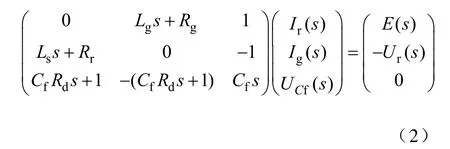
忽略Rg、Rr、Rd，由式（2）可得系统传递函数

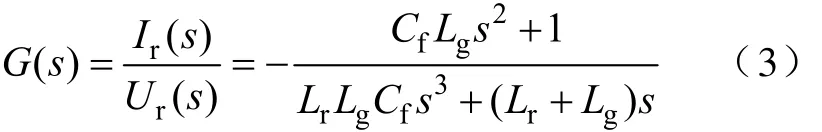
根据式（3）得到其谐振频率

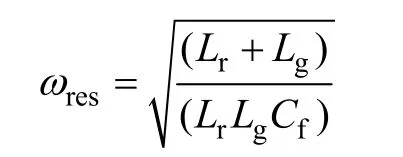
结合图2和图3状况，在离散域，系统控制框图如图4所示，图中电流调节器采用PI调节器，其参数选取采用“工程最优”方法进行选取，即

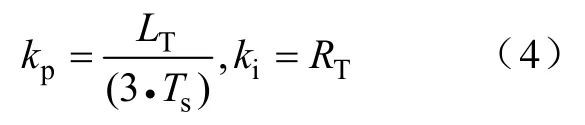
可以通过Tustin方法得到其离散化模型D（z）。对于系统传递函数模型 G（s），采用 PWM 控制方式时，通常有以下两种方式对其离散化：①将PWM环节 GPWM（s）等效为一个滞后时间常数为 TPWM的纯滞后环节，对其整体离散化；②采用零阶保持器的方法，如式（5）所示，将PWM更新引入的延迟等效为一拍滞后。本文采用第二种方法对其离散化。

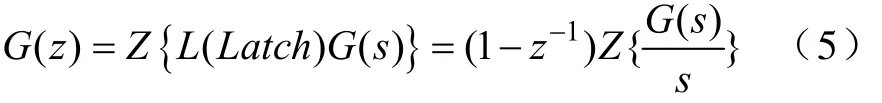
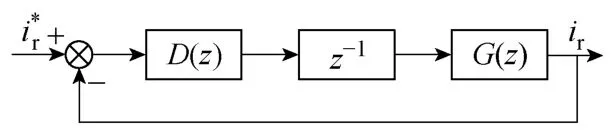
图4 离散域电流环控制框图Fig.4 Current control loop scheme in discrete domain

本文所分析的系统参数如下表所示。

表 系统主要参数Tab. The main parameters of three phase PWM rectifier

3.2 无源阻尼控制

当采用无源阻尼控制方法时，在LCL滤波器的滤波电容支路串联阻尼电阻如图1所示，那么系统传递函数为

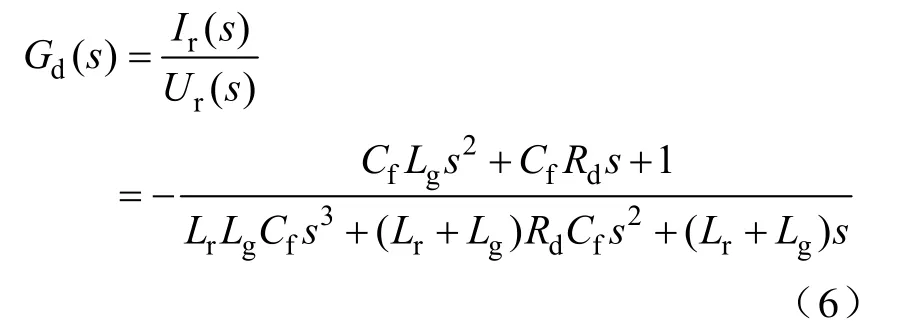
系统离散域闭环零级点分布如图5所示，可以看到随着阻尼电阻值增加，系统不稳定的极点由单位圆外移至单位圆内，系统稳定性增强。

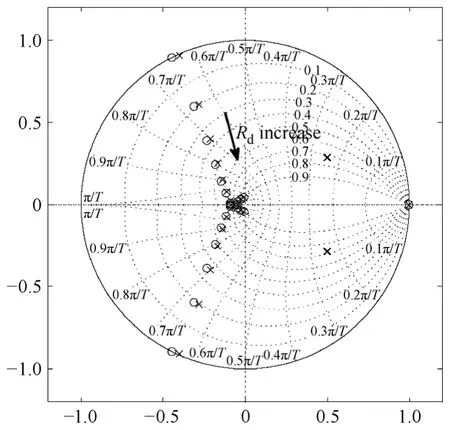
图5 采用无源阻尼控制时系统闭环零极点分布Fig.5 Close loop’s root locus for LCL filter with varying Rd

3.3 有源阻尼控制

LCL滤波器有源阻尼控制框图如图 6a所示，图中假设引入控制环节的电容电压与实际电容电压相等，忽略Rg、Rr、Rd时，控制框图可以等效为图6b所示。

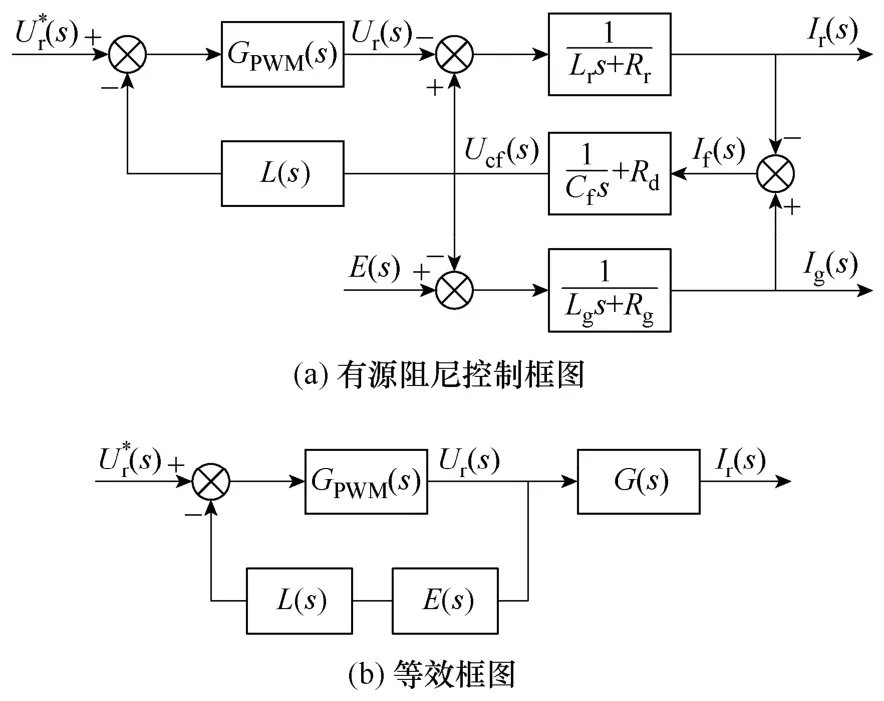
图6 LCL滤波器有源阻尼控制框图Fig.6 Active damping control diagram for LCL filter

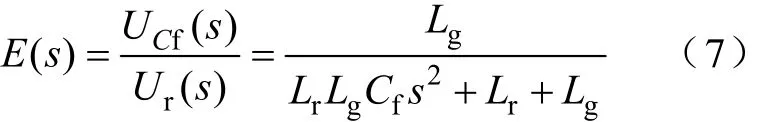
L（s）为超前—滞后（Lead-Lag）模块，其形式为

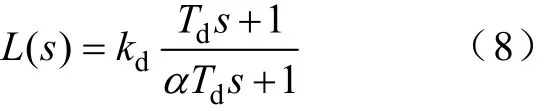
采用Tustin方法进行离散化后为

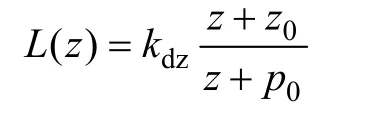
考虑电流环作用时的系统控制框图如图 7所示，图中为z-1电容电压采样引起的延时，那么有

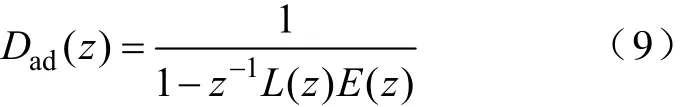
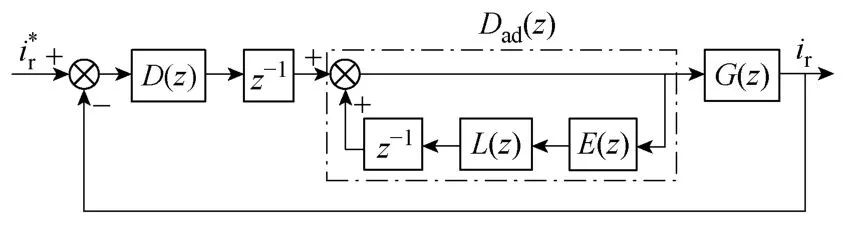
图7 考虑电流环作用时有源阻尼系统控制框图Fig.7 Current control loop with lead-lag active damping

采用有源阻尼控制方法时，系统离散域闭环传递函数为

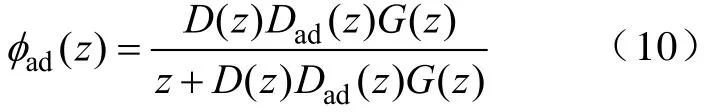
分析超前—滞后环节的 Bode图后表明，其本质上为高通滤波器，那么L（s）可以改写为

kdz变化时，系统闭环零极点分布如图8所示。图8表明，采用电容电压反馈的有源阻尼方法其本质是将滤波电容电压中的高频分量引入控制环节，在一定的kdz取值区间，系统是稳定的，系统控制框图如图9所示。图中，将滤波电容电压中的低频分量通过低通滤波器（Low Pass Filter, LPF）滤除得到其高频分量。算法的关键之处在于如何得到滤波电容上的电压，可以增加电容电压传感器方法获取，但是会增加系统成本。文献[8-9]提出了一种滤波电容电压 UCf观测方法，该方法通过对变流器输出电流进行微分获取电容电压的高频分量，缺点在于在实时数字控制系统中微分算法难以实现，并且会引入高频噪声，引起系统不稳定。

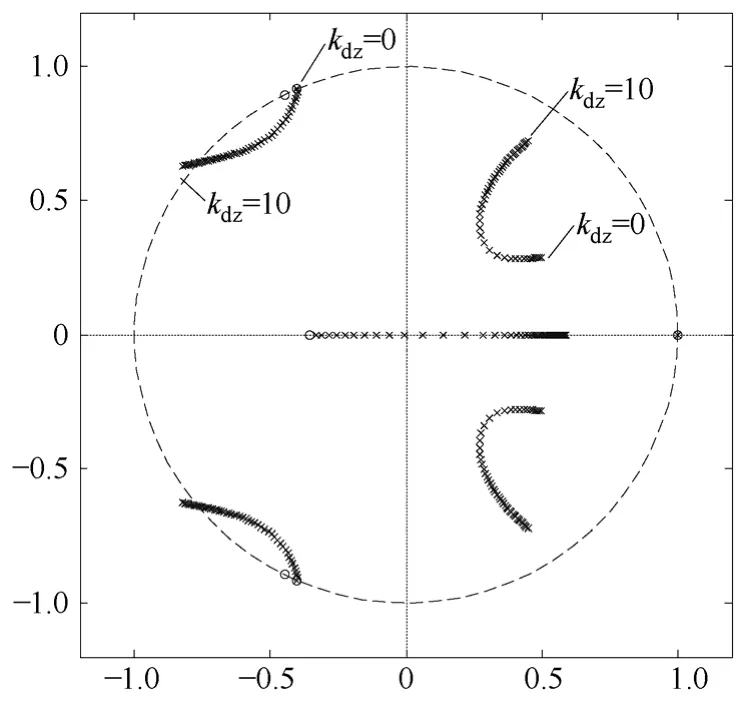
图8 kdz变化时系统闭环零极点分布Fig.8 Closed loop root locus with varying gain kdz

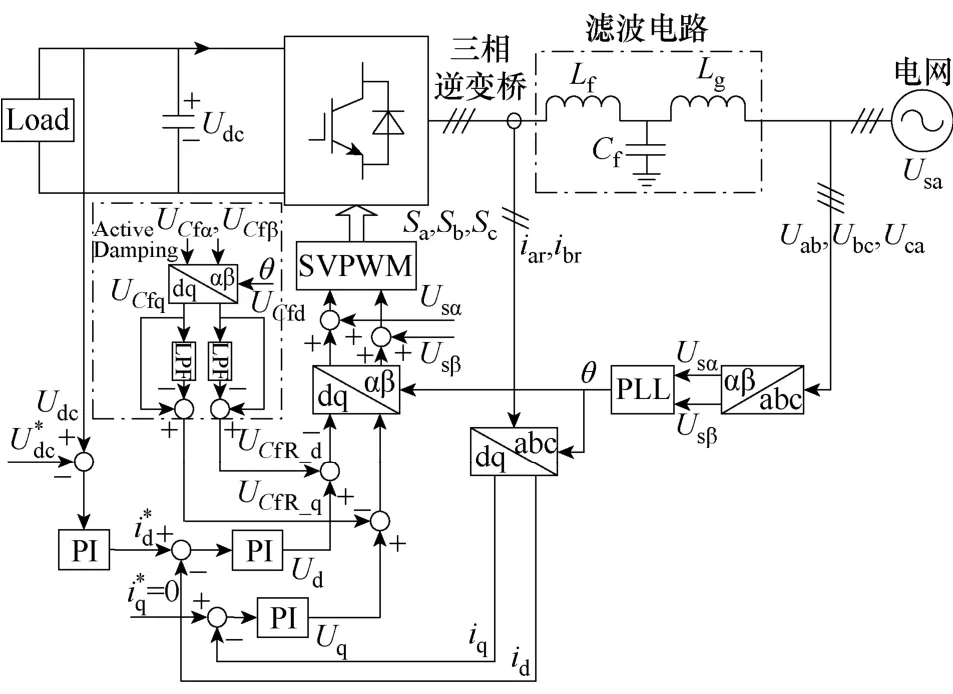
图9 采用AD控制方法时系统控制框图Fig.9 Control sheme of VOC with AD

LCL滤波器发生谐振时，忽略Rg、Rr，系统单相谐波等效电路如图10所示。

图10 系统谐振时单相谐波等效电路Fig.10 Single-phase harmonic equivalent model

图10所示中，假定电网中谐波电压为 0，Lg1为电网等效阻抗，esh为系统电网侧检测到的谐波电压，uCfh为电容谐波电压，ish为电容谐波电流，urh为逆变器输出谐波电压，那么，根据图10可以推知

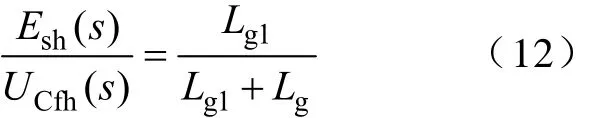
式（12）表明，电网侧检测到的谐波电压与电容谐波电压成比例关系，那么在有电网电压传感器的系统中，可以通过检测电网电压的谐波分量提取电容电压谐波分量uCfh进行有源阻尼控制。

4 仿真结果

采用 Matlab/Simulink对上述控制方法进行了仿真分析，仿真中母线电压Udc=800V，其他参数设置如表所示。

4.1 无源阻尼控制

图11所示为采用无源阻尼控制时仿真波形，设置阻尼电阻Rd=0.05Ω，图中分别为电网电压、电流及变流器输出电流波形，网侧电流与变流器侧电流THD值分别为1.61%、7.99%，LCL滤波器滤波效果显著。

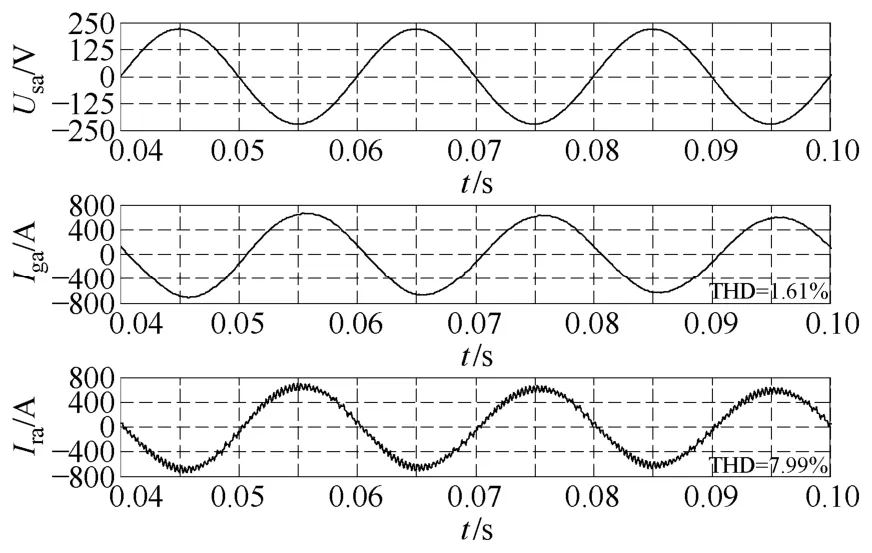
图11 采用无源阻尼控制时仿真波形图Fig.11 Simulation results of passive damping method

4.2 有源阻尼控制

图12所示为采用文中所提出的有源阻尼控制方法时的仿真波形，仿真中设置比例系数kdz=1，0.1s时启动有源阻尼控制，可以看到该方法对LCL滤波器的谐振很好地进行了抑制。图13所示为采用有源阻尼控制时，分别采样电网电压和电容电压得到的d轴前馈电压波形，可以看到，两者呈比例关系，与式（12）结论相符。

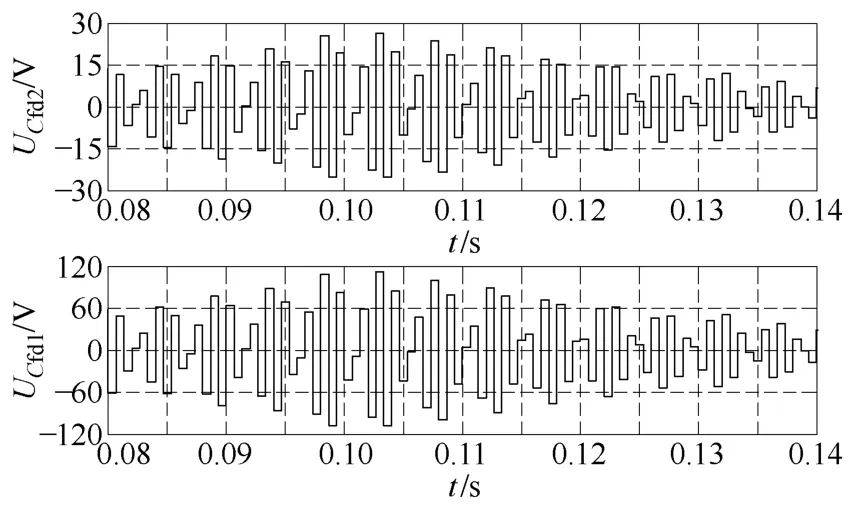
图13 两种电压采用方法获取的滤波电容d轴前馈电压Fig.13 Comparison of filter capacitor d axis voltage

5 结论

本文对 LCL滤波器谐振抑制方法进行了分析和研究，结论如下：

（1）采用阻尼电阻的无源方法可以简单、有效地抑制LCL滤波器谐振，但是会增加系统损耗。

（2）提出一种无传感器有源阻尼控制策略，将电网谐波电压引入控制环节，并考虑采样保持、PWM 更新引入的延时，控制算法简单，参数易于选取，仿真结果表明了所提方法的正确性。

[1]Komurcugil H, Kukrer O. A novel current-control method for three-phase PWM AC-DC voltage-source convertors[J]. IEEE Transactions on Industrial Electronics,1999, 46(3): 544-553.

[2]Karrari M, Rosehart W. Comprehensive control strategy for a variable speed cage machine wind generation unit[J]. IEEE Transactions on Energy Conversion,2005, 20(2): 415-423.

[3]Pekik Argo Dahono. A control method for DC-DC converter that Has an LCL output filter based on new virtual capacitor and resistor concepts[C]. Proceedings of the Annual IEEE Power Electronics Specialists Conference, 2004.

[4]张宪平, 李亚西, 林资旭, 等. LCL滤波的电压型PWM 整流器的有源阻尼抑制[J]. 电气传动, 2007,37(11).Zhang Xianping, Li Yaxi, Lin Zixu, et al. Active damping control of voltage source PWM rectifier with LCL filter[J]. Electric Drive, 2007, 37(11).

[5]Blasko V, Kaura, V. A novel control to actively damp resonance in input LC filter of a three phase voltage source converter[C]. IEEE Applied Power Electrionic Conference, 1996(2): 545-551.

[6]Hansen S, Malinowski M, Blaabjerg F. Sensorless control strategies for PWM rectifier[C]. Proceedings of the IEEE Applied Power Electrionic Conference,2000, 832-838.

[7]Malinowski M, Bernet S. A simple voltage source sensorless active damping scheme for three-phase PWM converters with a LCL filter[J]. IEEE Transactions on Industrial Electronics, 2008, 55(4):1876-1880.