基于振型差值曲率与神经网络的海洋平台结构损伤识别研究

于 菲， 刁延松， 佟显能， 张启亮

（1.青岛理工大学 土木工程学院 ，山东青岛 266033；2.山东同圆设计集团青岛分公司，山东青岛 266000）

结构损伤能够降低结构的刚度、增大结构的阻尼、改变结构的动态参数结［1］，因此可以利用结构损伤前后动力特性参数的变化进行结构损伤识别。如何利用结构动力参数的变化判断结构的健康状况是当前国际上的一个研究热点。

目前，比较成熟的损伤识别方法有［2，3］：① 损伤指标法，主要指标有：坐标模态确认准则、改进的坐标模态确认准则、模态应变能指标、振型曲率指标、模态柔度指标以及模态刚度指标等；② 模型修正法；③ 灵敏度分析法；④ 反分析法；⑤ 神经网络法，与传统的模式识别方法相比，它具有容错性、鲁棒性、自组织性、自适应性、便于实施监测和过滤噪声的能力。因此，神经网络在损伤检测领域得到了广泛的应用。

但对于大型复杂结构，单独使用以上方法，存在许多问题［4］：① 复杂结构的构件数目众多，输入数据量大，如果直接利用神经网络测试，可能会造成输入数据爆炸，网络规模过大以致难以收敛；② 复杂结构的自由度数较大，而实际所能测得的数据要少很多，测试数据的不完备可能导致以上各种方法的失效；③ 指标法对于简单结构有比较理想的效果，但对复杂结构，只能指出损伤的大概区域。

针对上述问题，本文提出了一种两步识别法。第一步，利用振型差值曲率得到损伤的大致区域；第二步，在第一步所得到的区域内，利用BP神经网络确定损伤构件的准确位置。该方法的优点是：第一步，仅需要少量低阶模态分量，无需考虑高阶模态分量；进行第二步识别时，由于缩小了识别范围，从而减少了网络输入数据的数量，减小了网络规模，提高了计算效率，因此，该方法可以用于大型复杂结构的损伤识别。四层海洋平台数值模拟和实验结果验证了该方法的有效性。

1 基本原理

第一步：利用振型差值曲率确定损伤区域

结构损伤必将导致结构刚度发生变化，刚度的降低致使结构损伤前后振型发生变化。但振型的变化对损伤并不是很敏感。曲率能够反映结构中性面的变形，即公式：

式中，v″（x）、M（x）、E和I分别为构件截面处的曲率、弯矩、弹性模量和截面惯性矩。由式（1）可以看出，结构的曲率与刚度成反比，刚度的降低势必将导致曲率发生很大的变化。因此，可以利用振型的差值计算得到振型的差值曲率，从而得到对损伤更为敏感的损伤指标。

结构损伤前后的振型差值定义为：

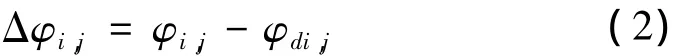
式中，φi，j与φdi，j分别为结构损伤前后第j阶振型第i测点的位移振幅。

结构振型差值曲率定义为：

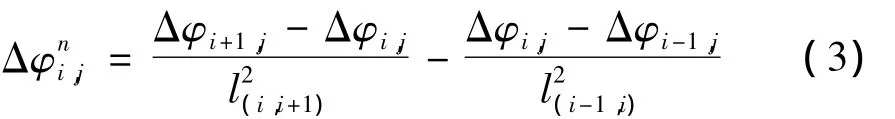
式中，l（i，i+1）为节点i与节点i+1 之间的距离，Δφi+1，j，Δφi，j，Δφi－1，j分别为第j阶振型第i+1，i，i－1 节点的振型差值。

在结构发生损伤的位置，单元两端节点的振型发生比较大的变化，通过曲率运算将此变化放大，从而得到损伤的位置。此方法对平面结构有比较好的定位效果，但对大型复杂空间结构，仅能确定大致的损伤区域，因此需要第二步精确的损伤定位。

第二步：基于BP神经网络的损伤精确定位

有关BP神经网络的基本原理参见文献［5，9］。

在第一步的基础上，得到可能损伤的区域，在此区域内做更为精确的损伤定位，这样网络的输入参数得到极大的缩减，从而减小了网络规模，提高计算效率。

对于网络的输入参数，可以有多种形式，本文取陈长征等［4］提出的损伤指标向量作为网络输入参数：

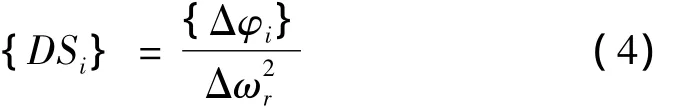
式中，{DSi}为对应于第i阶模态的损伤指标向量，Δφi为损伤前后第i阶的振型变化量，Δ为损伤前后第r阶频率变化量的平方。

为了将输入向量控制在［－1，1］之间，这里采用归一化的损伤指标：

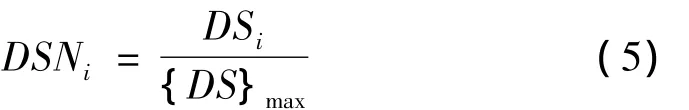
式中：{DS}max为损伤指标向量中绝对值的最大值。

此损伤指标不需要完备的模态信息，只要选择几个测点的模态分量就够了，因此该方法可以用于测试模态信息不完备的大型复杂结构的损伤识别。

2 数值仿真

本文采用一四层海洋平台数值模型（如图1所示）进行数值仿真，采用ANSYS建立了该平台的三维有限元模型。基本参数为：弹性模量为 E=2.07e+11 N/m2，密度为：7 800 kg/m3，共有32个节点，192个自由度，50个BEAM4单元，9个 SHELL63单元，4个MASS21单元（模拟甲板上设备以及建筑物），7种单元截面类型，海洋平台与基础固接。

各种损伤工况均采用降低单元弹性模量来实现，模拟的损伤工况见表1。

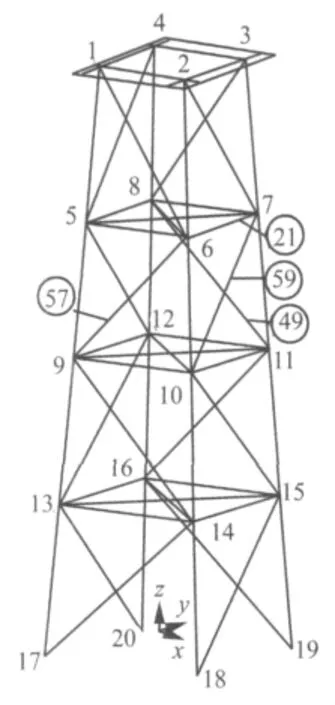
图1 海洋平台模型图Fig.1 Offshore platform

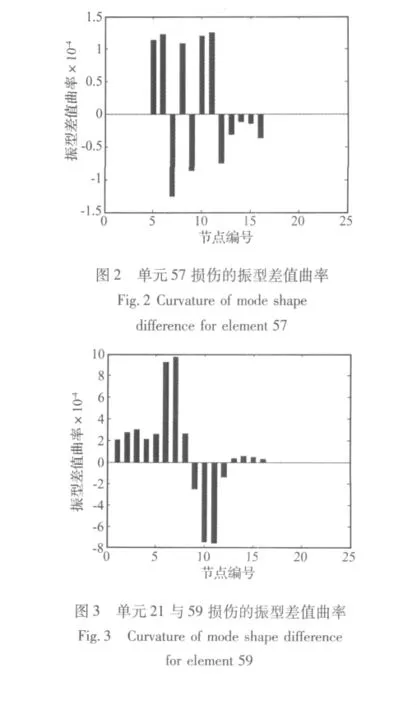
表1 损伤工况Tab.1 Damage cases

首先进行第一步损伤识别，取结构第一阶位移振型计算各节点的振型差值曲率，仅对甲板之下的塔架进行检测，所以只需计算1～20节点的振型差值曲率。对于工况1与工况2均取结构Y向第一阶位移振型来计算各节点的振型差值曲率（X与Y方向见图1）。利用MATLAB编制相应的计算程序，计算出各节点的振型差值曲率，结果如图2和图3所示，由图2与图3 可以得出损伤的大致区域，见表2。

表2 损伤的大致区域Tab.2 General damage areas

表3 工况1网络训练与检测样本Tab.3 network training and testing samples for case 1

第二步识别：在确定损伤的大致区域后，利用前三阶固有频率和 X 向第一阶模态在节点5、6、9、10、13、14处的X向水平分量计算损伤指标。损伤指标进行归一化后（由于篇幅所限，在此数据将不再列出）输入到建立好的BP网络进行训练。对于输出结果，当小于0.1时，则表示此处没有损伤，大于0.9则表示此处存在损伤。

工况1（单元57损伤80%）：结构可能损伤的单元见表2，网络训练样本见表3。此工况网络结构采用6×13×20，有关的网络训练参数为：最大训练次数取1000；训练精度为1e－5；学习率取0.05；动量因子取0.9。

表4 工况1网络测试结果Tab.4 Network test results for case 1

训练结束后，将测试样本数据输入到训练好的神经网络中，得到测试结果如表4。

由表4的测试结果可以看出，利用训练好的神经网络可以准确地识别出损伤单元为57，与假定的损伤位置一致。

工况2（单元21与单元59损伤80%）：可能损伤的单元见表2。网络训练样本与测试样本如表5。此工况网络结构采用6×9×10，训练参数为：最大训练次数取1000；训练精度为1e－5；学习率取0.05；动量因子取 0.9。

训练结束后，将测试数据输入到训练好的网络中，所得测试结果见表6。

由表6的测试结果可以看出，经过第二步的神经网络测试，可以准确识别出工况2的损伤单元为单元21与单元59，与假定的损伤位置一致。

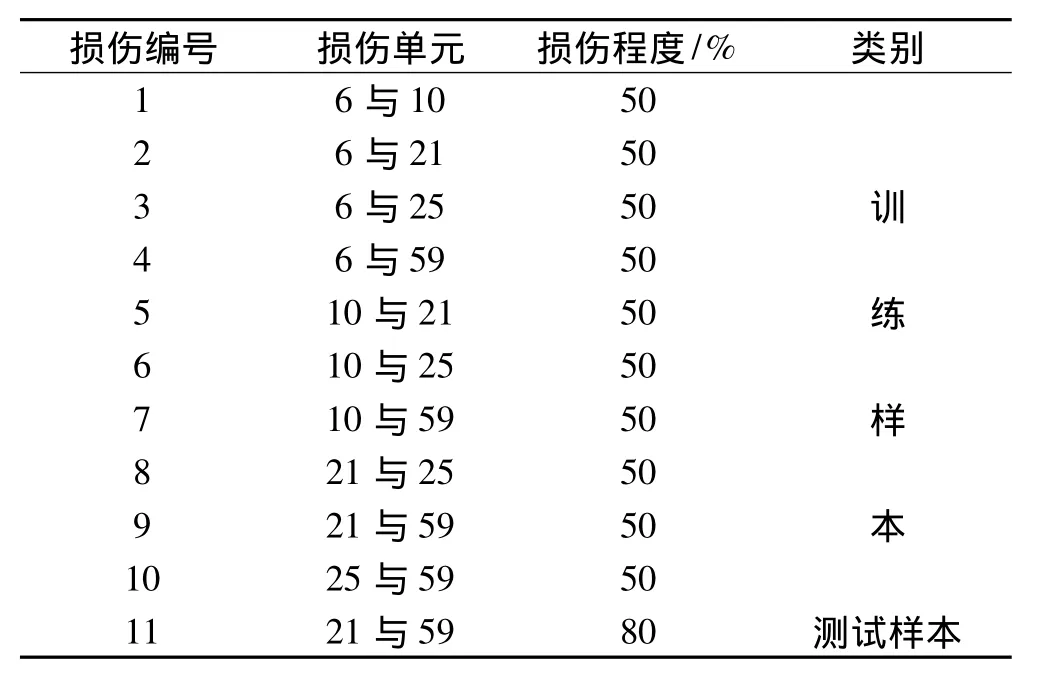
表5 工况2网络训练与测试样本Tab.5 Network training and testing samples for case 2

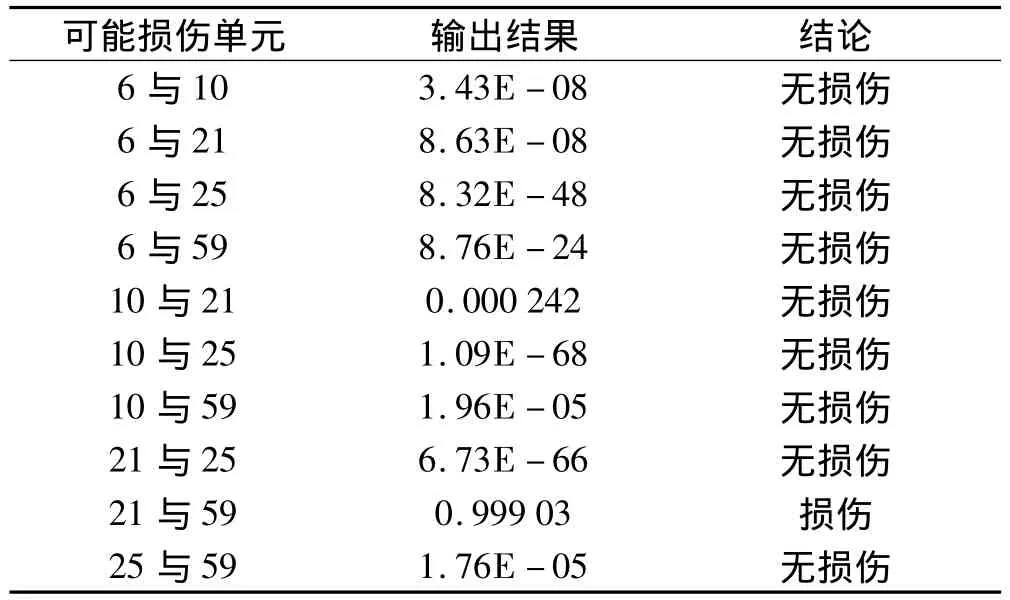
表6 工况2网络测试结果Tab.6 Network test results for case 2

3 实验验证

为了进一步验证本文提出的两步法的可行性，利用海洋平台模型支撑损伤的冲击响应实验与振动台实验数据［10］进行了验证，其中实验模型与数值模拟中的模型一致（如图3.1所示）。实验模态参数识别采用标量型ARMA法。仅采用了实验中的单损伤工况，损伤杆件均为斜撑。具体的损伤工况见表7。

第一步损伤识别：对于工况1与工况2均采用Y向第一阶振型。各节点的振型差值曲率如图4与图5所示，由图4与图5可以得出损伤的大致区域，见表8。

表7 损伤工况Tab.7 Damage cases

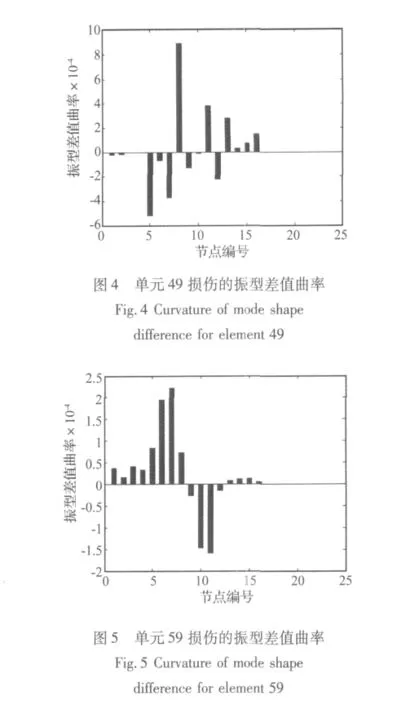
由表8可以得出，在实际实验中，振型差值曲率法可以识别出损伤的大致区域。

第二步损伤识别：在确定损伤的大致区域后，首先利用数值模拟数据来训练神经网络，网络训练好后，由实验数据计算网络测试向量，将测试向量输入到网络中进行测试，得到更为精确的识别结果。网络输入向量采用前3阶频率与X向第一阶模态在节点5、6、9、10、13、14处的X向水平分量计算得到。

表8 损伤的大致区域Tab.8 General damage areas

工况1（单元49损伤100%）：结构可能损伤的单元见表8。网络训练样本见表9。网络结构采用6×10×19，有关的训练参数为：最大训练次数取500；训练精度为1e－5；学习率取0.05；动量因子取0.9。训练结束后，将测试数据输入，得出的测试结果见表10。

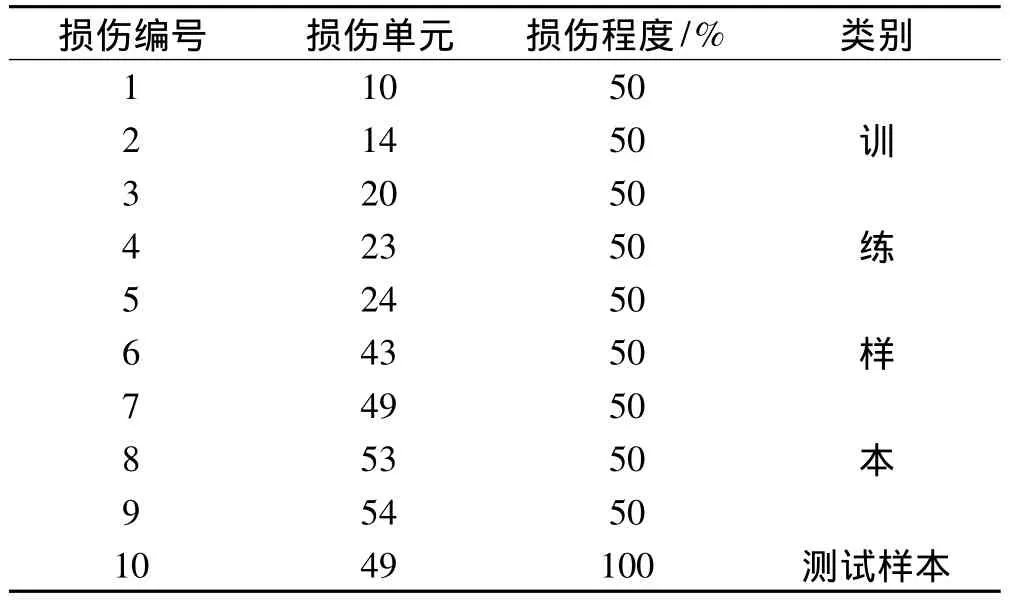
表9 工况1训练与测试样本Tab.9 network training and testing samples for case 1

表10 工况1测试结果Tab.10 Network test results for case 1

工况2（单元59损伤100%）：可能存在损伤的单元见表8。网络训练样本如表11。网络结构采用6×10×5，有关的训练参数为：最大训练次数取500；训练精度为1e－5；学习率取0.05；；动量因子取0.9。训练结束后，将测试数据输入，测试结果见表12。

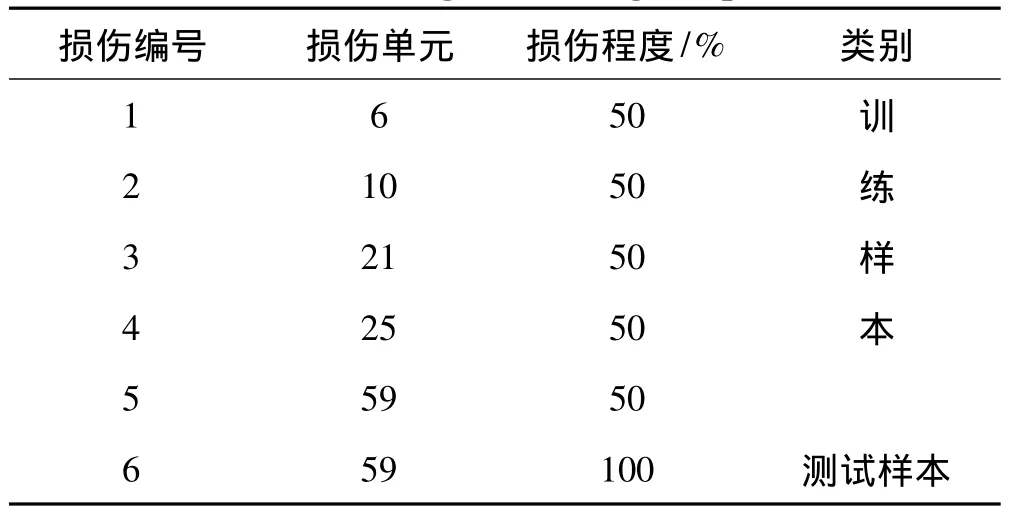
表11 工况2训练与测试样本Tab.11 network training and testing samples for case 2

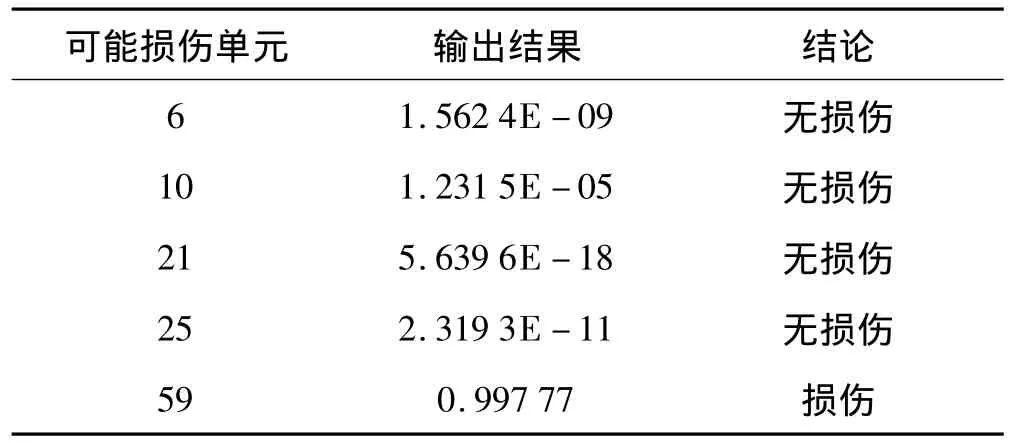
表12 工况2测试结果Tab.12 Network test results for case 2

经过两步损伤识别，可以准确识别出上述两种实验工况中损伤单元的位置，验证了本文所提出的两步法的可行性。

5 结论

本文提出了一种结构损伤识别的两步法，首先利用振型差值曲率得到大致的损伤区域，然后，利用BP神经网络在该损伤区域内进行精确的损伤定位。该方法不仅可以大大减少网络训练样本的数量，避免了网络规模过大导致的不收敛问题，而且仅需低阶模态部分测点的水平分量信息，因此，该方法可以应用于模态信息不完备的大型复杂结构的损伤识别。四层海洋平台数值仿真与实验结果验证了该两步法的可行性。

［1］Charles R F，Scott W D，David A N.Vibration based structure damage identification［J］.The Royal Society，Philosophical Transactions：Mathematical Physical and Engineering Sciences，2001，359（1778）：131 －149.

［2］瞿伟康，黄东梅.大型复杂结构的两阶段损伤诊断方法［J］.世界地震工程，2003，19（2）：72－78.

［3］郭惠勇，李正良，彭 川.结构损伤动力识别技术的研究与进展［J］.重庆建筑大学学报，2008，30（1）：140 －145.

［4］刁延松，李华军，李 军，等.一种框架结构损伤诊断两步法［J］.工业建筑，2005，35（S1）：966－969.

［5］陈长征，罗跃纲，白秉三，等.结构损伤检测与智能诊断［M］.北京：科学出版社：183－233.

［6］罗跃纲，彭永恒，闻邦椿.工程结构的集成神经网络识别研究［J］.振动与冲击，2006，25（1）：14 －17.

［7］Oh B H，Jung B S.Structural damage assessment with combined data of static and modal tests［J］.Journal of Structural Engineering，ASCE ，1998，124（8）：956－965.

［8］罗晓健，于国良.几种模态分析方法在结构无损检测中的应用［J］.中国海洋平台，2006，21（5）：44 －49.

［9］董长虹.Matlab神经网络与应用［M］.北京：国防工业出版社：1－106.

［10］刁延松.基于神经网络和小波分析的海洋平台结构损伤检测研究［D］.青岛：中国海洋大学，2006.