流体作用下正交各向异性圆锥壳的自由振动

曹雄涛，华宏星

（上海交通大学 机械系统与振动国家重点实验室，上海 200240）

圆锥壳体在很多工程应用中被广泛使用。在航空航天飞行器、潜艇中，圆锥壳体是一个常用的结构单元。Rayleigh-Ritz法被用来研究圆锥壳的自由振动［1，2］。Galerkin 法 被 用 来 研 究 圆 锥 壳 的 振 动 特性［3－7］。其圆锥壳体的模型是基于 Love-Timoshenko的薄壳理论。Shu［8］运用广义微分积分法研究了层合圆锥壳的自由振动。Liew［9］用kp－Ritz法分析了薄锥壳的自由振动，讨论了不同边界条件下的频率特性。Crenwelge和 Muster［10］研究了正交加筋圆锥壳体的振动，这是早期的加筋锥壳的研究工作。能量法和假设模态法被用来求解纵横加筋壳体的振动。一些研究人员［1，11］也用这种方法分析了正交加筋复合壳体的自由振动。这种方法的不便之处在于控制方程不能显式获得。Mecitoglu［12，13］研究了加筋各向同性锥壳的自由振动。通过平均能量法，环筋和纵骨的惯性和刚度融合到锥壳里面。一个简单的正交各向异性圆锥壳得到了。由于这种理论的局限性，这种模型仅在低频范围内是有效的。融合筋法（smeared theory）也被Goldfeld［14］用来研究螺旋筋加强锥壳的屈曲稳定性分析。Tong［15］研究了复合锥壳的自由振动，解是通过幂级数法获得的。但是其结果并不是精确的解析解，尽管有较好的精度。Caresta和Kessissoglou［16］分析了各向同性锥 － 柱组合壳的自由振动特性。锥壳通过幂级数法求解。在周向波数为1，自由－自由边界条件下，Donnell-Mushtari壳体方程产生错误的频率。传递矩阵法［17.18］被用来研究锥壳的固有频率。有限元法［19－21］被用来分析锥壳的自由振动。Sofiyev［22］研究了功能梯度（FGM）锥壳的稳定性和非线性振动。

圆锥壳体声辐射的研究工作比较少。Guo［23］利用多尺度技术研究了弹性波在流体载荷下锥壳中的传播。将流体载荷作用下的圆柱壳的控制方程通过摄动来研究锥壳的动力特性。这种研究仅仅是一种渐近分析。Caresta和Kessissoglou［24］用幂级数序列求解了流体作用下锥壳的动力响应。流体通过将圆锥分段成小锥壳，这些小锥壳被当作圆柱壳，然后确定每一小段圆柱的流体载荷。然而，对于母线方向以幂级数序列表示的位移场，他们的模型中，没有给出母线方向的波数km是如何确定的。幂级数序列似乎不适合于声辐射，因为幂级数序列不能直接同波数相关。而且对于流体载荷，km是至关重要的，这一点能从本文中看到。

在本文研究中，波传播法被用来分析流体加载下的正交各向异性圆锥壳体的自由振动。波传播法被一些研究人员用来分析圆柱壳的振动特性［25－27］。根据边界条件，母线方向的波数km是已知的。这种性质对于处理流体载荷是方便的。圆锥的流体载荷用多个小段圆柱的流体载荷来逼近。应用壳体和流体间的界面边界条件和求解圆柱坐标系下的Helmholtz方程，就分段获得了圆锥壳体的流体载荷。给出了确定流体载荷的详细过程。圆锥壳体的运动方程是基于Reissner－Naghdi薄壳理论，并且利用Galerkin法求解。研究了圆锥的自由振动和流体载荷对圆锥的影响。对于稳态振动，在本文中时间因子e－iωt略去不写。

1 圆锥壳体的运动方程

一个薄壁正交各向异性圆锥壳显示在图1中。l1和l分别是圆锥壳体小端母线方向的长度和大端母线方向的长度。u1，u2和u3是壳体中面在母线方向α1，圆周方向α2和法向方向α3的位移。曲线坐标和位移场显示在图1中。

图1 圆锥壳体曲线坐标和中面位移Fig.1 The curvilinear coordinates and displacements of middle surface for conical shell

其中，q1，q2，q3和pa分别是表面力载荷作用在α1，α2，α3方向和流体载荷。Lij是微分算子，它们是：

其中，I1是正交各向异性圆锥壳体的面密度，其值为I1=ρch。ρc和h是圆锥壳的体积密度和厚度。α是圆锥壳体的半锥角。正交各向异性圆锥壳体的材料参数Aij和Dij定义如下：

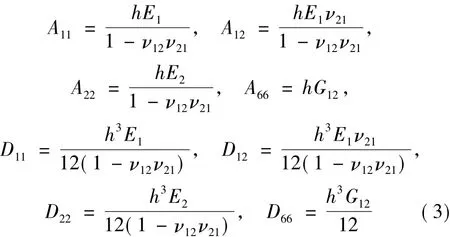
其中，E1，E2，ν12，ν21和G12是正交各向异性圆锥壳体材料的弹性常数。正交各向异性材料的Poisson比有如下关系：

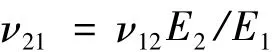
正交各向异性圆锥壳体的位移场用波传播的形式可以写为：

其中，km是母线方向波传播因子，其值由边界条件决定。通常km能选为与锥壳边界条件相似的Euler梁的波传播因子［27］。通过把方程（4）代入（1），方程（1）是解耦的对于参数α2，但对于参数α1是耦合的。通过运用Galerkin法到方程（1），加权积分的Galerkin过程能写为：

像Lam［7］那样处理：在方程（5）中的耦合项被忽略，例如：cos［km（α1－l1）］cos［kd（α1－l1）］和sin［km（α1－l1）］sin［kd（α1－l1）］，m≠d。这些耦合项的贡献非常小。

2 流体载荷和积分过程

Moon和Spencer［28］用分离变量法研究过Helmholtz方程的解，指出Helmholtz方程能在40种正交曲线坐标系下用分离变量法求解。Helmholtz方程在锥壳的正交曲线坐标系中是不能用分离变量法来处理的。因此，一个分段流体加载方法用来近似圆锥壳体的流体载荷，如图2所示。

2.1 流体载荷

流体介质中的声压满足柱坐标系下的Helmholtz方程：

面向分布式光伏虚拟集群的有源配电网多级调控//窦晓波,常莉敏,倪春花,段向梅,葛浦东,吴在军//(3):21

其中，流体域中的波数k0为ω/c，c是流体中的声速。Laplace算子为：

其中，α1，α2和α3分别是轴向、周向和径向坐标。第j个圆锥段（被近似为圆柱壳段）与流体间的边界条件为：

将方程（6），方程（8）和方程组（4）的第三个方程联立起来，运用Sommerfeld远场辐射条件，就获得了第j个圆锥段的流体载荷：

图2 圆锥壳段的划分和一个流体加载的圆柱壳Fig.2 Strips of conical shells and a strip of fluid loaded circular cylindrical shell

2.2 壳体表面压力在Galerkin法中的处理

如果圆锥壳体被划分为s段圆柱壳，锥壳的流体载荷pa由s段以方程（9）的形式表示的流体载荷组成。运用方程（9），流体载荷在方程（5）中的贡献pmnε可以写为：

式中的积分很容易获得。其中，一些耦合项像前面的处理那样被忽略。这些耦合项的贡献很小。

3 流体加载圆锥壳体的自由振动

设外力q1，q2和q3为零，将方程（4），方程（9）代入方程（5），得到：

其中，系数Cij是非常复杂的表达式，涉及到材料参数、角频率和壳体的几何参数。仅仅系数C11在附录中给出，其它系数可以用相似的方法得到。对于真空中的圆锥壳，特征方程（11）能够用线性代数的方法求解；对于流体加载的圆锥壳，用迭代法求解。

4 数值结果

在本节中，利用前面的理论，研究了各向同性和正交各向异性圆锥壳体的自由振动。对于方程（11），有三类不同的固有频率。最低的频率对应锥壳的径向运动，其它两个固有频率主要代表纵向运动或周向运动。无量纲频率定义为：

比率γ12定义为：

固有频率以ωc的形式给出，并且给出的频率对应锥壳径向振动模态。锥壳浸没在水中。水中声速为c=1 500 m/s，质量密度为ρ=1 000 kg/m3。锥壳被划分为s=20段圆柱壳来逼近锥壳的流体载荷。

4.1 模型的有效性验证

将频率参数同Lam［6］给出的结果作了比较。各向同性锥壳的参数为h/b=0.01，ν=0.3，（l－l1）sinα/b=0.25。表1给出了真空中简支锥壳的固有频率。母线方向的波数为mπ/（l－l1）。

表1 简支锥壳的频率 ωc，h/b=0.01，ν=0.3，（l－l1）sinα/b=0.25，m=1Tab.1 The nondimensional frequency ωcof a simply supported conical shell h/b=0.01，ν =0.3，（l－l1）sinα/b=0.25，m=1

可以看出当前给出的结果同Lam给出的结果符合得很好。锥壳的频率随周向波数的变化规律为：初始时逐渐减小，然后逐渐增加。

下一个例子用来比较流体载荷下很小锥角的圆锥壳和相似结构圆柱壳的固有频率。张［26］利用波传播法分析了流体载荷作用下简支圆柱壳的固有频率。圆柱壳的参数如下：长度、半径和厚度分别是20 m，1 m和0.01 m；质量密度、Poisson比和弹性模量分别为：7 850 kg/m3，0.3 和2.1 ×1011Pa。圆锥小端半径为 1 m，大端半径为1.04 m。锥壳半锥角为0.114 591 6°。l1为500 m，l为520 m。圆锥在母线方向的长度为20 m。材料参数同圆柱一样。锥壳和柱壳都浸没在水中。图3给出了流体载荷作用下的锥壳和柱壳的固有频率。对比显示小锥角锥壳与柱壳的流固耦合振动固有频率符合得很好。表明当前方法处理流体载荷是有效的。图3显示：在低周向波数时，流体中的锥壳的固有频率下降了对应于真空中锥壳的频率大约一半。

4.2 各向同性圆锥壳体的振动

对于各向同性圆锥，弹性模量E为2.1×1011Pa，泊松比ν为0.3，密度ρc为7 800 kg/m3和厚度h为0.006 m。锥壳小端半径a是0.2 m，大端半径b是0.8 m。l1和l分别是0.66 m 和2.667 m。锥角为34.916°。锥壳两端边界条件为简支－简支（SS）。

图4显示了SS边界条件下锥壳的耦合和未耦合固有频率。未耦合和耦合模态分别对应真空中的锥壳和浸没在流体中的锥壳。从图中能够看出流体和锥壳是强烈耦合的。在低周向波数时耦合频率几乎下降到未耦合频率的一半。在高周向波数时，耦合频率大约下降了四分之一。在分析流体与锥壳相互作用时，流体的影响必须要考虑。对于两端简支的锥壳，图5显示了锥壳分段数s对耦合频率收敛特性的影响。s=5与s=20的频率值是相同的，表明频率已经收敛。耦合频率收敛速度很快，s的取值比较灵活。

4.3 正交各向异性圆锥壳体的自由振动

对于正交各向异性圆锥壳，在计算中使用两个壳体模型。两个模型的材料参数是E1=E=2.1×1011Pa，E2=E1/γ12，ν12=0.3，G1=E1/［2（1+ν12）］和ρc=7 800 kg/m3。流体介质是水。两个模型中的边界条件是SS。第一个锥壳模型的几何参数像4.2节那样保持不变。第二个锥壳模型的几何参数与第一个模型相同，只是下面几个参数改变了：锥壳大端半径b为1.2 m，l1为0.4 m，l为2.4 m，锥角为60°。图6－图9显示了比率γ12对有无流体加载下锥壳固有频率的影响。通过比较图6－图7和图8－图9，可以看到流体载荷改变了锥壳的自由振动特征。在低周向波数时，流体载荷使得锥壳的频率下降了一半；在高周向波数时，锥壳的频率下降了四分之一。低周向波数时，流体载荷强烈影响着锥壳的动力特性。当比率γ12从2增加到20时，图6－图9显示ωc下降，并且周向波数的增加轻微地改变了ωc。这是因为当γ12增加时，与母线方向刚度相比，周向刚度变弱了。这种变弱的周向刚度放松了对ωc的贡献。对于大的γ12，ωc主要依赖于母线方向刚度。

图6 γ12对ωc的影响，半锥角为α=17.458°，没有流体载荷，m=1Fig.6 Effect of γ12on ωcfor conical shell with half vertex angle α =17.458°，without fluid load，m=1

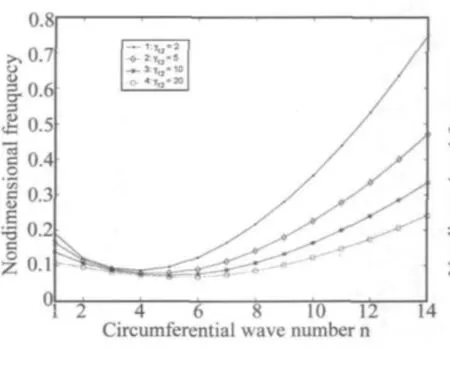
图7 γ12对ωc的影响，半锥角为 α =17.458°，有流体载荷，m=1Fig.7 Effect of γ12on ωcfor fluid loaded conical shell with half vertex angle α =17.458°，m=1

图8 γ12对ωc的影响，半锥角为α=30°，没有流体载荷，m=1Fig.8 Effect of γ12on ωcfor conical shell with half vertex angle α =30°，without fluid load，m=1

图9 γ12对 ωc的影响，半锥角为α=30°，有流体载荷，m=1Fig.9 Effect of γ12on ωcfor fluid loaded conical shell with half vertex angle α =30°，m=1

5 结论

给出一个包括流体载荷作用的圆锥壳自由振动理论模型。一个技巧而又系统的锥壳自由振动的解通过波传播法和Galerkin法得到。将圆锥壳分段用圆柱壳近似，流体载荷易于处理。波传播法适合于确定流体与锥壳的耦合效应。因为锥壳和声场都体现了波动。本文的数值结果同其他研究者的结果相符，表明了给出的模型是有效的。研究了不同边界条件下锥壳自由振动特征。分析了弹性模量比率γ12对正交各向异性圆锥壳体频率ωc的影响。γ12越大，ωc就越小。数值结果显示流体载荷强烈影响结构的动力特性。在低周向波数时，锥壳的耦合频率下降了大约一半；高周向波数时，锥壳的耦合频率下降了大约四分之一。本文的研究可以应用到潜艇艉部锥壳的声辐射上。

［1］ Talebitooti M，Ghayour M，Ziaei-Rad S，et al.Free vibrations of rotating composite conical shells with stringer and ring stiffeners［J］.Archive of Applied Mechanics，2010，8：1 －15.

［2］ Li F M，Kishimoto K，Huang W H.The calculations of natural frequencies and forced vibration responses of conical shell using the rayleigh-ritz method［J］.Mechanics Research Communications，2009，36（5）：595 －602.

［3］Hua L.Influence of boundary conditions on the free vibrations of rotating truncated circular multi-layered conical shells［J］.Composites Part B：Engineering，2000，31（4）：265 －275.

［4］Hua L.Frequency characteristics of a rotating truncated circular layered conical shell［J］.Composite Structures，2000，50（1）：59－68.

［5］ Lam K Y，Hua L.Vibration analysis of a rotating truncated circular conical shell［J］.International Journal of Solids and Structures，1997，34（17）：2183 －2197.

［6］ Lam K Y，Hua L.Influence of boundary conditions on the frequency characteristics of a rotating truncated circular conical shell［J］.Journal of Sound and Vibration，1999，223（2）：171－195.

［7］ Lam K Y，Hua L.On free vibration of a rotating truncated circular orthotropic conical shell［J］.Composites Part B：Engineering，1999，30（2）：135 －144.

［8］Shu C.Free vibration analysis of composite laminated conical shells by generalized differential quadrature［J］.Journal of Sound and Vibration，1996，194（4）：587 －604.

［9］ Liew K M，Ng T Y，Zhao X.Free vibration analysis of conical shells via the element-free kp-ritz method［J］.Journal of Sound and Vibration，2005，281：3 －5，627 －645.

［10］ Crenwelge Jr O E，Muster D.Free vibrations of ring-andstringer-stiffened conical shells［J］.Journal of Acoustical Soc America，1969，46（1，2）：176 －185.

［11］Zhao X，Liew K M，Ng T Y.Vibrations of rotating cross-ply laminated circular cylindrical shells with stringer and ring stiffeners［J］.International Journal of Solids and Structures，2001，39（2）：529－545.

［12］ Mecitoglu Z.Vibration characteristics of a stiffened conical shell［J］.Journal of Sound and Vibration，1996，197（2）：191－206.

［13］ Mecitoglu Z.Governing equations of a stiffened laminated inhomogeneous conical shell［J］.AIAA Journal，1996，34（10）：2118－2125.

［14］ Goldfeld Y.Elastic buckling and imperfection sensitivity of generally stiffened conical shells［J］.AIAA Journal，2007，45（3）：721－729.

［15］ Tong L.Free vibration of composite laminated conical shells［J］.International Journal of Mechanical Sciences，1993，35（1）：47－61.

［16］ Caresta M，Kessissoglou N J.Free vibrational characteristics of isotropic coupled cylindrical-conical shells［J］.Journal of Sound and Vibration，2010，329（6）：733 －751.

［17］ Irie T，Yamada G，Muramoto Y.Free vibration of joined conical-cylindricalshells［J］. JournalofSound and Vibration，1984，95（1）：31 －39.

［18］ Irie T，Yamada G，Tanaka K.Natural frequencies of truncated conical shells［J］.Journal of Sound and Vibration，1984，92（3）：447－453.

［19］PatelB P， GanapathiM，KamatS. Free vibration characteristics of laminated composite joined conicalcylindrical shells［J］.Journal of Sound and Vibration，2000，237（5）：920－930.

［20］ Buchanan G R，Wong F I.Frequencies and mode shapes for thick truncated hollow cones［J］.International Journal of Mechanical Sciences，2001，43（12）：2815 －2832.

［21］ El Damatty A A，Saafan M S，Sweedan A M I.Dynamic characteristics of combined conical-cylindrical shells［J］.Thin-Walled Structures，2005，43（9）：1380 －1397.

［22］ Sofiyev A H，Kuruoglu N，Halilov H M.The vibration and stability of non-homogeneous orthotropic conical shells with clamped edges subjected to uniform external pressures［J］.Applied Mathematical Modelling，2010，34：1807 －1822.

［23］ Guo Y P.Fluid-loading effects on waves on conical shells［J］.Journal of Acoustical Society of Americ，1994，97（2）：1061－1066.

［24］ Caresta M，Kessissoglou N J.Vibration of fluid loaded conical shells［J］.Journal of the Acoustical Society of America，2008，124（4）：2068－2077.

［25］ Gan L，Li X，Zhang Z.Free vibration analysis of ringstiffened cylindrical shells using wave propagation approach［J］.Journal of Sound and Vibration，2009，326：（3 － 5）：633－646.

［26］ Zhang X M.Frequency analysis of submerged cylindrical shells with the wave propagation approach［J］.International Journal of Mechanical Sciences，2002，44（7）：1259 －1273.

［27］Zhang X M，Liu G R，Lam K Y.Coupled vibration analysis of fluid-filled cylindrical shells using the wave propagation approach［J］.Applied Acoustics，2001，62（3）：229 －243.

［28］ Parry Moon D E S.Field theory handbook［M］.Berlin Springer-Verlag，1988.

附录同其它系数Cij相比，系数C11有最简单的表达式。其它系数Cij能够用相似的方法得到。

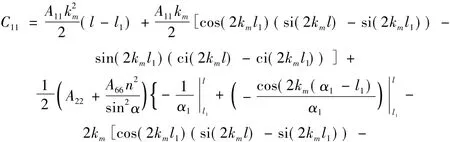
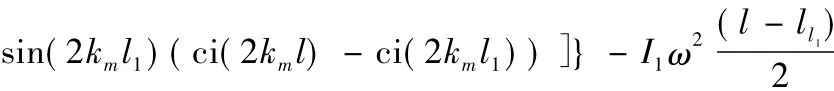
其中，sine积分函数si（x）定义为：

cosine积分函数ci（x）定义为：