模态自适应相位调制的多压电元件压电分流系统

杨智春，孙 浩

（西北工业大学 航空学院，西安 710072）

近年来，压电分流阻尼抑振技术在振动控制研究领域得到了很高的关注［1］。作为一种新颖的被动振动抑制技术，它利用压电材料的正压电效应，将结构振动的机械能转变成电能，通过分流电路中的发热电阻将电能转化为热能消耗掉，从而对机械振动系统产生抑制振动的阻尼作用，具有结构简单、鲁棒性好的优点，在振动控制领域有着广泛的应用前景。

为了提高压电分流系统的振动控制效果，不仅可以通过对单个压电元件的结构形式进行优化，例如尺寸优化［2］、形状优化或拓扑优化［3］，也可通过对多个压电元件进行布局优化来提高压电元件的能量转化效率。在这几种方法中，采用多个压电元件的布局优化是将压电分流技术推向工程应用的最现实和最佳的途径，得到了众多研究人员的关注［4－6］。但在含有多个压电元件的压电分流系统的构建中，各压电元件在结构的不同模态振动响应下的输出电压之间出现相位差，使得各压电元件极化表面的诱发电荷发生中和抵消现象，降低了压电分流系统的效率。而在压电分流阻尼系统的结构抑振应用中，用手动方法根据结构实际的模态响应进行各压电元件电极间的连接调节是不现实的，国内外的研究中对这种现象以及解决方法均没有明确的分析和讨论［7－9］。

本文从含有多个压电元件的压电分流系统的等效电压源网络组建策略出发，提出了几种典型的等效电压源网络拓扑结构，分析了压电元件在不同阶次的模态响应下的输出电压之间的相位关系，提出了具有模态自适应能力的相位调制技术和相应的电路模块设计思路。

1 多压电元件分流系统的组网策略

在压电分流系统的构建中，为达到较好的振动机械能到电介能的转化效果，往往采取较大尺寸的压电元件或者多个压电元件，但是由于较大尺寸的压电元件存在诸如制作困难、对布局空间要求高等限制，在实际应用中往往难以实现，多个压电元件的构建方案成为众多研究工作者关注的对象。而在组建分流电路网络时，对多个压电元件之间相互连接关系的处理也存在多种选择，网络拓扑结构主要有以下三种：

① 图1（a）所示的独立连接，各压电元件之间互不相连，而是各自连接有分流电路。

② 图1（b）所示的串联连接，相邻两个压电片的下极化表面和上极化表面相连，最终的整体电压源的两极分别为1#PZT的上极化表面和N#PZT的下极化表面；

③ 图1（c）所示的并联连接，各压电元件的上极化表面全部连接到一起组成整体电压源的一个电极，同样将下极化表面连接到一起组成另外一个电极，在这两个电极之间连接分流电路阻抗；

在这三种连接方式中，从能量转化效果的角度来讲，方式①是较为理想的方案，各压电元件诱发电荷互不影响，可使能量转化量最大化，其缺点在于连接的分流电路太多，需对每个分流电路的参数进行优化，构建工作量及成本随压电元件的数量成正比增加，较难实现。

图1 不同联接的压电元件Fig.1 Piezo elemento in different of kinds

方式②中各压电元件极化表面的电荷量是相同的，最终的电荷数量取决于诱发电荷数量最少的压电元件，这严重限制了全部压电元件的能量转化量。并且，任意两个压电元件之间的连接断开都将导致整个系统的失效，可靠性很低。

方式③中各压电元件并联，电荷是根据各压电元件的电压相等的原则进行分布。在能量转化效果上，方式③接近方式①，远高于方式②；在电路和参数优化的复杂性方面，方式③与方式②相同，只需要一个分流电路，远简单于方式①。综合而言，方式③可以较好地避免方式①和方式②的不足，是一种较为可行的优选方案。

2 多个压电元件输出电压间的相位关系

连接方式③的缺点在于：各压电元件的上极化表面被连接到一起，这就要求各压电元件上极化表面所携带的诱发电荷的极性相同，否则将出现不同压电元件的极化表面极性相反的电荷中和抵消的现象，使一部分电荷不能够进入分流电路而使压电分流抑振效果降低。

图2 布局优化的压电元件在四边固支薄板结构两阶模态下的变形Fig.2 The deformation of PZTs under different modes of the clamped plate

以图2所示的四边固支薄板结构的布局优化结果为例［10］，两个压电片之间采用并联连接方式，1#PZT和2#PZT的上极化表面连接到一起作为一个电极，二者的下极化表面连接到一起作为另一个电极，在两个电极之间连接分流电路进行抑振。在第1阶（1，1）模态下，1#PZT和2#PZT对称的分布于振型中的凸峰两侧，二者均产生拉伸应变，两个压电片的上极化表面或下极化表面的电荷极性相同，不会有诱发电荷中和抵消的现象。但是在图2（b）的第3阶（1，2）模态下，1#PZT位于振型中的凸峰上，产生拉伸应变，而2#PZT位于振型中的凹谷上，产生压缩应变。1#PZT和2#PZT的上极化表面产生的诱发电荷的极性是相反的，同样两者下极化表面的电荷极性也是相反的，若不改变两者之间的并联连接方式，则不可避免的出现正负电荷中和抵消，降低压电分流系统的抑振效果。在对各压电片的输出电压幅值归一化后，图2（a）和图2（b）中的压电片1#PZT、2#PZT和整体等效电压源的电压幅值和相位关系见图3，可以看到同一种连接方式在第1阶和第3阶模态下的整体电压源的幅值分别是1和0，差别很大，严重影响了压电分流系统的抑振效果。因此必须针对连接方式③进行改进，也就是对压电元件的电压进行相位调制以避免相互间电荷的中和。

图3 1#PZT、2#PZT和整体等效电压源的电压幅值和相位关系Fig.3 The amplitude and phase of 1#PZT，2#PZT and integral equivalent voltage source

3 模态自适应的相位调制方法

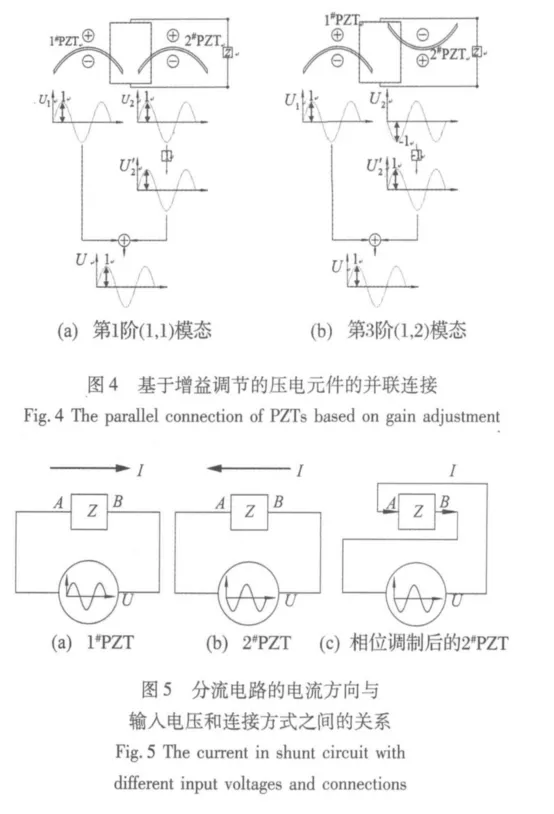
假设1#PZT的输出电压U1为主电压，2#PZT的输出电压U2为从电压，通过改变U2的相位来实现与U1的相位同步输出，以保证在结构各阶模态响应下，各压电元件的输出电压在接入到分流电路时均处于同相状态。具体实现方式是，在2#PZT接入并联的网络前，对U2进行增益处理，增益K的值为1或－1，绝对值均为1，即不改变U2的幅值，仅改变相位，如图4所示。

在U1和U2同相时，原信号不作处理，K=1，U'2=U2，直接接入网络；在U1和U2如图4（b）所示的反相时，K=－1，对U2进行倒相，U'2=－U2，然后再接入网络。增益的具体实施如图7所示。

图5是不同压电片的输出电压施加在分流电路的两端产生的电流，图5（a）是主电压的情况，UAB=U=U1，图5（b）是从电压的情况，UAB=－U=U2=－U1，而图7（c）中分流电路与压电元件的连接端A和B被互换，UAB=－1·UBA=－1·（－U）=U，AB之间的电压恢复到图5（a）所示的情况，相位调制的具体实现方式是改变压电元件的两个极化表面与分流电路之间的连接方式。由于各压电元件在结构各阶模态下的输出电压均为同相或反相，仅在结构相邻固有频率之间一个远离压电分流阻尼系统抑振频带的很窄频率范围内，是一种介于同相和反相之间的相位关系，所以上述方法对各阶固有频率处的稳态响应或结构瞬态响应的抑制均是有效的。

4 模态自适应相位调制器的设计思路

实际结构受到的动态激励频率往往是变化的，会覆盖结构多阶固有模态的频率，例如图2中的第1阶和第3阶模态，当激励频率在这两阶模态频率间变化时，1#PZT和2#PZT输出电压的相位关系也随之在同相和反相之间变化，因此针对各压电元件输出电压的相位调制系统，必须能够实时地根据结构振动响应的变化来改变各压电元件的输出电压之间的相位关系，其设计思路如图6所示。

在压电元件输出电压的相位调制系统的构建中，首先选择其中的一个压电元件作为主压电元件，其输出电压信号为主电压信号，其余所有压电元件的输出电压均为从电压信号；然后，针对每一个从压电元件，将其输出电压信号与主电压信号相乘；将经过相乘的信号进行整流，再与设定的阈值电压进行比较，从而发出合适的控制电压来决定是否对从电压信号进行倒相操作，这样使所有经过相位调制处理的从电压信号均达到了与主电压信号同相的状态，将这些输出电压信号与主电压信号设定为并联连接状态，统一接入分流电路网络，进行压电分流抑振。

5 模态自适应相位调制器的仿真验证

图6 模态自适应相位调制系统的工作原理Fig.8 Working principle of modal adaptation and phase shifter

在确定模态自适应相位调制器的设计思路后，本文完成了模态自适应相位调制器电路模块的详细设计，然后采用仿真软件EWB进行模态自适应相位调制器电路的仿真调试，模拟其工作特性，仿真电路见图7。

在仿真电路中，采用两个交流稳压源分别表示主、从压电元件的输出电压信号，即主电压源和从电压源，两者的幅值均设为1 V，频率为100 Hz，而相位相反，即如图3（b）所示的情况，选用阻值为1 000 Ω的负载电阻模拟分流电路的输入阻抗。

仿真中设定了3种工况：① 不采用模态自适应相位调制器，将主、从电压源手动设置为同相，并联连接负载电阻；② 不采用模态自适应相位调制器，将主、从电压源直接并联，接入负载电阻；③ 采用模态自适应相位调制器，将从电压源首先接入模态自适应相位调制器，再将模态自适应相位调制器的输出电压与主电压源并联接入负载电阻。在工况①下，负载电阻的工作电流为1 mA，等于理论值；在工况②下，两电压源反相接入负载电阻，负载电阻的工作电流值为0.438 μA，可以认为两电压源的电势相互抵消，没有电流流经负载电阻；而在工况③下，负载电阻的工作电流也为1 mA，与工况①相同，说明模态自适应相位调制器实现了对电压源理想的反相操作，使主、从电压最终同相的施加在负载阻抗上，模态自适应相位调制器的输入阻抗特性对负载阻抗的工作也没有造成任何不利影响。仿真结果表明，模态自适应相位调制器能够可靠而良好地完成相位调制操作，可以应用于多压电元件压电分流系统。模态自适应相位调制器的电路实物见图8。

图7 模态自适应相位调制器仿真电路Fig.7 Circuit of mode adaptation and phase shifter in simulation

图8 模态自适应相位调制器电路模块Fig.8 Circuit module of modal adaptation and phase shifter

6 结论

本文从含有多个压电元件的分流系统的等效电压源网络组建策略出发，总结了几种典型的等效电压源网络拓扑结构，分析了各自的优缺点，确立并联连接作为最终的等效电压源组网方式。分析了在结构不同阶次的模态响应下，含有多个压电元件的压电分流系统的各压电元件的输出电压之间的相位关系，提出相应的等效电压源相位调制思想。设计了能够自动跟踪结构振动响应的模态阶次的相位调制电路，带有这种相位调制电路的压电分流系统，能够避免各压电元件极化表面不同极性的诱发电荷产生中和抵消而降低压电分流系统抑振效果的问题。利用EWB仿真软件进行了模态自适应相位调制器电路模块的仿真。仿真结果表明，模态自适应相位调制器可以准确的实现多个压电元件的输出电压之间的相位处理，使这些信号全部处于同相状态再输入到分流电路中。模态自适应相位调制器良好工作效果使压电分流阻尼抑振系统在抑振应用中不必考虑各压电元件输出电压之间相位关系，简化了多压电元件压电分流阻尼抑振系统的构建。

［1］Hagood N W，Von Flotow A.Damping of structural vibration with piezoelectric materials and passive electric networks［J］.Journal of Sound and Vibration，1991，146（2）：243－268.

［2］ Wu D，Yang Z C，Sun H，et al.Vibration control effectiveness of piezoelectric shunt damping system［C］.The Fourth International Conference on Smart Materials for Engineering＆Biomedical Application/The Third International Conference on Smart Materials＆Structures in Aerospace Engineering（4thSMEBA ＆ 3rdSMSAE），Nanjing：Nanjing University of Aeronautics ＆ Astronautics，2008，75 －81.

［3］Sun H，Yang Z，Li K，et al.Vibration suppression of hard disk driver actuator arm using piezoelectric shunt damping with topology optimized PZT Transducer［J］.Smart Materials and Structures，2008，18（6）：1 －13.

［4］ Hollkamp J J，Gordon R W.An experimental comparison of piezoelectric and constrained layer damping［J］.Smart Materials and Structures，1996，5：715 －722.

［5］Quek S T，Wang S Y，Ang K K.Vibration control of composite plate via optimal placement of piezoelectric patches［J］.Journal of Intelligent Material Systems and Structures，2003，14：229－245.

［6］ Suresh V Venna，Lin Y J.Optimal placement piezoelectric transducers for passive vibration control of geometrically nonlinear structures［J］.Proceedings of ASME International Mechanical Engineering Congress ＆ Exposition，Anaheim：ASME，2004，1 －7.

［7］Wu S Y.Multiple PZT transducers implemented with multiple mode piezoelectric shunting for passive vibration damping［J］.Proceedings of SPIE，Newport Beach，S mart Structures and Materials，1999，3672，112 －122.

［8］Kim S J，Yun C Y，Paek B J.Optimal design of a piezoelectric passive damper for vibrating plates［J］.T.Tupper Hyde，Proceedings of SPIE，Smart Structures and Materials，2000，3989，512 －519.

［9］ Petit L，Lefeuvre E，Richard C，et al，A broadband semi passive piezoelectric technique for structural damping［J］.Kon-Well Wang，Proceedings of SPIE，Bellingham：Smart Structures and Materials，2004，5386，414 －425.

［10］ Sun H，Yang Z C，Li K X，et al.Experimental study on placement optimization of transducers of piezoelectric shunt damping system for plate vibration［C］.Spencer B F，Tomizuka M，Yun C B，et al.World forum on smart materials and smart structures technology （SMSST’ 07），Taylor＆Francis，2007，492.