挡块对斜拉桥横向抗震体系的影响

徐略勤，李建中

（同济大学 土木工程防灾国家重点实验室，上海 200092）

自1955年第一座现代斜拉桥在瑞典建成以后，斜拉桥的理论研究和工程实践得以飞速发展［1］。由于其外形美观、造价合理、施工方便以及型式多样，斜拉桥在200 m～1 000 m的跨度范围内倍蒙垂青，其抗震性能也相应地得到越来越多的关注和研究。国内对斜拉桥纵向和横向抗震体系的研究开展的非常广泛，但大部分集中在纵向飘浮体系的合理约束装置及其参数的选取［2，3］；以及边跨横向约束形式的影响分析上［4，5］。相比于纵向的抗震问题，斜拉桥横向的抗震体系显然更为复杂。通常在斜拉桥的横向约束体系中，主梁与索塔间设置抗风支座，而主梁与边墩间常设置限位支座或适当的限位装置。这种相对刚性的连接往往会引起结构的横向地震响应过大，导致边墩及其基础成为全桥结构的抗震薄弱环节。此外对于采用横向限位挡块的斜拉桥，主梁与挡块间的碰撞问题不容忽视。地震引起结构物的碰撞容易导致严重的破坏性后果，而目前对斜拉桥碰撞问题的研究相比梁桥要少得多，而且考虑的基本上是主桥与引桥在过渡墩处的碰撞现象［6］。因此地震作用下限位挡块对斜拉桥横向抗震体系的影响是桥梁设计人员感兴趣的未知因素，本文结合一工程实例采用非线性动力时程分析方法对限位挡块的影响进行具体的探讨，依据减隔震原理提出若干降低桥梁结构地震响应的办法并加以比较研究，在此基础上建议最合理的横向抗震体系。

1 动力分析模型

1.1 桥例简况

本文采用宁波大榭第二大桥（图1）作为工程背景进行相关的分析。该工程主桥结构为双塔单索面钢箱梁斜拉桥，跨径布置为（50+158+392+158+50）m，全桥总长808 m。桥塔为“帆”型混合塔，锚固区为钢结构，中下塔柱为混凝土结构，索塔总高138.291 m，其中桥面以上部分高100.162 m。主梁采用单箱三室钢箱截面，标准段顶板宽29.5 m，底板宽17.5 m。每边跨处分别设一锚墩和边墩，基础均采用高桩承台基础。结构体系为：索塔与主梁横向设置限位支座，纵向自由但每个塔梁连接处设有2个粘滞阻尼器；主梁与锚墩之间横向设有限位支座，纵向可自由活动；边墩处设置双向活动支座。主桥支座均为防海洋腐蚀环境的球形钢支座，锚墩和边墩的盖梁两侧均设置抗震挡块以限制梁体位移。

图1 大榭第二大桥总体布置图（单位：mm）Fig.1 Elevation view of the Daxie Bridge（unit：mm）

1.2 结构有限元模型

采用三维有限元模型进行结构的地震响应分析，主梁、索塔、墩均用梁单元模拟，并考虑恒载轴力对单元几何刚度的影响；拉索采用空间桁架单元模拟，同时考虑恒载作用下的几何刚度变化，并根据Ernst提出的等效弹性模量法［7］来考虑垂度效应；桩基础在冲刷线以上用梁单元模拟，在冲刷线以下采用集中土弹簧加以模拟。在场地可能遭受的罕遇地震下，斜拉桥会表现出高度的非线性行为，如支座的屈服、梁体与侧向限位挡块间的碰撞、阻尼器的耗能等。为了合理描述斜拉桥的地震响应特征，必须在有限元分析模型中对上述非线性行为进行有效的模拟。

图2所示的力－变形关系用以描述活动球型钢支座，其中Fy为支座的屈服强度，取其摩擦强度，摩擦系数取2%；dy为支座的屈服变形，此文取1 mm；k0为支座的初始刚度，k0=Fy/dy；kr为屈后刚度，文中取kr=1/10 000k0。

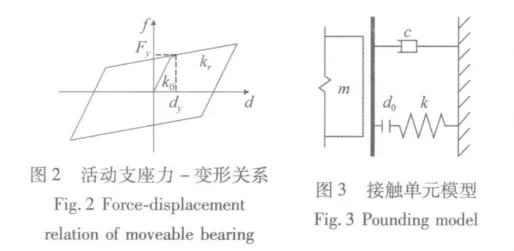
采用接触单元（图3）对主梁在强震作用下与挡块之间的碰撞效应进行模拟［8，9］。接触单元的非线性力－位移关系可表示为：

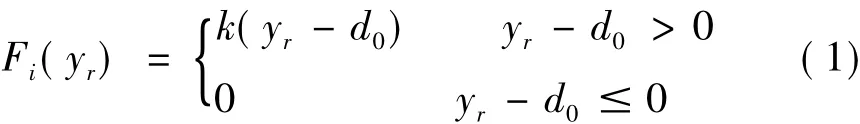
式中，d0为接触单元的初始间隙；yr为主梁与墩顶间的相对位移；k为接触刚度，假设本桥采用尺寸长×宽×高为400 cm×30 cm×50 cm的钢筋混凝土挡块，可取其弯曲刚度并考虑剪切变形的影响为k=7.5×106kN/m。

液压粘滞油阻尼器由活塞、油缸和节流孔组成，这类装置利用活塞前后压力差使油流过节流孔产生阻尼力。一般可采用精确的Maxwell阻尼计算模型进行模拟，在该模型中，阻尼力与相对变形的速度关系为：

其中，k为弹簧刚度；dk为阻尼器的变形量；c为阻尼系数，本文中如未特别说明均取c=3 000；d为阻尼器变形速度；exp为阻尼指数，取exp=0.3。

1.3 地震动输入

本文主要分析挡块对斜拉桥横向抗震体系的影响，因而仅考虑100年超越概率为3%的6条桥址场地的人工地震加速度时程（其峰值加速度均为177 cm/s）作为地震的横向输入，地震反应分析结果取6组反应的平均值。图4（a）为6条人工波对应的反应谱，（b）为其中一条典型的人工加速度时程曲线TH－1。

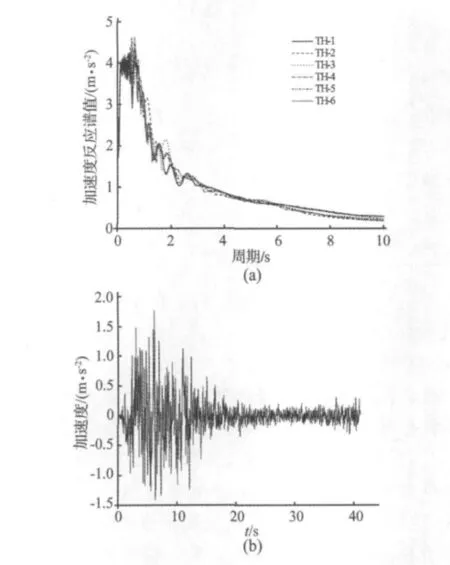
图4 地震动输入Fig.4 Ground motion input

2 结构响应分析

2.1 忽略挡块影响的地震响应分析

在当前的桥梁结构设计过程中，挡块通常被当作一种构造措施或是安全储备，在静力和动力分析中往往不予考虑。因此本文首先在忽略挡块作用的情况下，采用非线性时程分析法对大榭大桥初始的横向约束体系（主梁在横向与索塔、锚墩处设固定球型钢支座，而与边墩处则设活动球型钢支座）进行了数值模拟，其计算结果见表1。

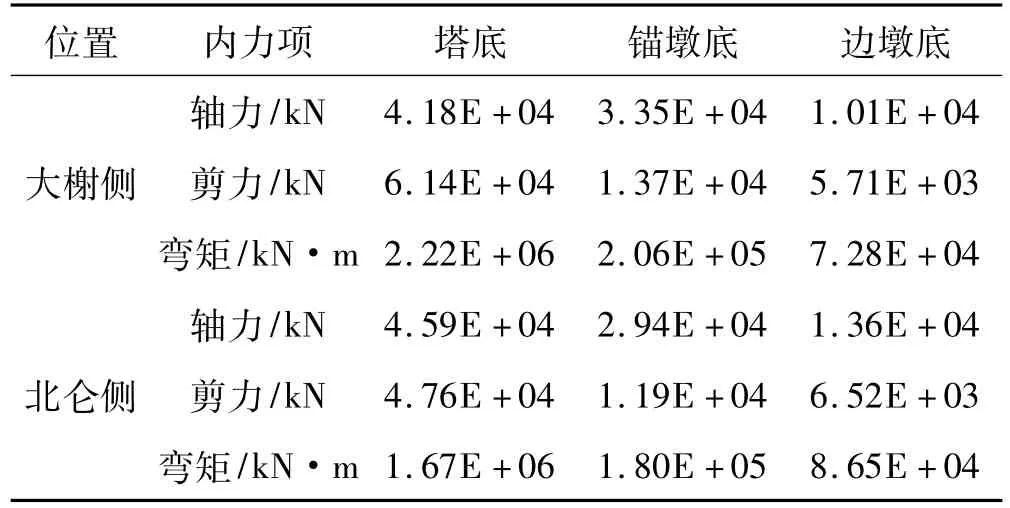
表1 关键构件最大内力响应（忽略挡块作用）Tab.1 Maximum internal forces of critical components without considering retainer influences

在不考虑挡块作用的前提下，两侧锚墩处的固定支座横向剪力需求分别达到了17 201 kN和16 986 kN，所有活动支座的横向变形均超过100 mm，最大达到119.6 mm，这无疑增添了支座的设计难度，不仅仅是经济上的代价，而且过大的侧向位移通常是不允许的。

2.2 考虑挡块影响的地震响应分析

根据前面的结果可知，不设置挡块或者分析时不考虑挡块的作用会导致支座的剪力和位移需求过大。就本桥而言，固定球形钢支座的抗剪强度约为10%的竖向承载力，即7 000 kN，而活动球形钢支座的横向位移能力仅为50 mm，因而支座在强震下难免发生破坏。为了探究挡块对斜拉桥横向抗震体系的影响，本文分别就以下三种情况进行讨论：

工况一：根据工程中常用的简化方法，忽略挡块自身的特性和碰撞效应，仅考虑挡块对梁体的侧向限位功能，采用主梁在横向与索塔、锚墩和边墩均为固结的体系来近似考虑挡块对主梁的约束作用；

工况二：考虑挡块发挥限位作用，强震下固定支座被剪断，但活动支座完好。采用图3所示的接触单元模拟挡块与主梁间的相互作用，但忽略碰撞效应，即取初始间隙为d0=0；

工况三：考虑主梁与挡块间的碰撞效应，并取初始间隙d0=5 cm，同时考虑强震下固定和活动支座破坏以后，主梁在支座剪断面上所受的摩擦力，其摩擦系数取 0.5［10］。

表2的结果为三个分析工况下索塔、锚墩和边墩的内力与表1各个对应项的比。

两索塔由于桩基础局部冲刷高度的不同导致横向刚度略有差异，北仑侧索塔偏柔，因此从受力上看大榭侧控制索塔的抗震设计。根据表2的结果可以发现，考虑挡块的作用以后，较柔的北仑侧索塔，结构响应变化不大，但横向刚度相对较大的大榭侧索塔地震反应则可能会明显下降（工况三）。从表2可知，边墩的地震需求在三个工况下均有一定幅度的增加，但由于其需求在数值上比锚墩小很多（表1），因此并不控制设计。实际上对斜拉桥而言，控制全桥横向抗震设计的一般是锚墩［6］，而本桥例中锚墩（尤其是大榭侧的锚墩）的地震需求在工况三下均得以大幅下降。

在考虑了梁体与挡块间的碰撞效应以后，大榭和北仑两侧索塔的塔底弯矩分别为1.768×106kN·m和1.673×106kN·m，数值非常接近。与不考虑挡块作用的体系（表1）相比，塔底控制弯矩（最大设计值）下降了20.3%，锚墩墩底控制弯矩（最大设计值）下降33.5%。当然，锚墩墩底地震响应的下降不仅仅因为挡块的作用，也有因固定支座剪断而导致的梁体横向惯性力在锚墩和边墩之间相对更均匀的分配引起。实际上，梁体在强震下的侧向位移由于两索塔横向刚度不同而不对称，碰撞现象的出现恰使梁体的不对称侧移得到一定程度的限制和重分配，从而使两塔受力更趋均匀，而且控制索塔设计的大榭侧，索塔内力大幅下降，节约了建设成本。

表2 关键构件最大内力响应比Tab.2 Ratios of maximum internal forces of critical components

图5表示的是在时程波TH－1激励下，锚墩和边墩上的挡块所受到的梁体侧向撞击力时程，图中正负值分别代表一个墩上两侧挡块方向相反的撞击力（下图同）。可以看到梁体与挡块间的碰撞现象在相当长的时间范围内均有发生，如边墩处的碰撞现象从地震发生约2 s后开始一直持续到18 s左右，最大撞击力达到13 909 kN；而锚墩处梁体与挡块间的碰撞次数没有边墩那么频繁，但最大撞击力却达到了16 848 kN。

图5 撞击力时程Fig.5 Time history of pounding forces

图6显示的是在工况二和工况三下，北仑侧锚墩和边墩处挡块的剪力TH－1时程图。由图可见，在主梁与挡块的间隙为0（工况二）的情况下，梁体的侧向惯性力大部分被锚墩处的挡块所吸收，边墩处的挡块作用相对较弱；而在梁体和挡块间设置一定的间隙以后（工况三），锚墩和边墩处的挡块受力则相对接近，说明此时边墩处的挡块更加有效地分担了主梁的惯性力，这对减小控制桥梁横向抗震设计的锚墩的受力非常有利，表2的数据结果也证明了这一结论。

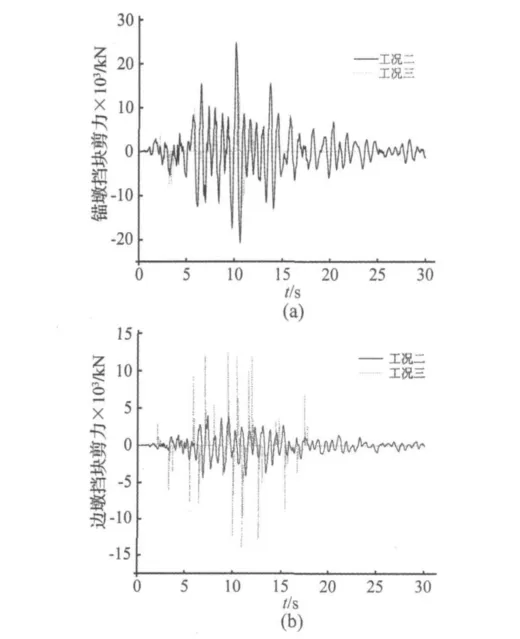
图6 挡块剪力时程Fig.6 Time history of shear forces of retainers

2.3 挡块失效的位移响应分析

从前面的分析可知，要保持挡块的有效性，挡块需要有足够的抗剪能力（超过10 000 kN），这对于尺寸有限的挡块来说有时很难实现。假如挡块无法承受主梁的侧向撞击而发生破坏，此时桥梁的横向约束体系完全失效，因此有必要对挡块破坏后结构的侧向位移进行评估。

图7 关键节点位移时程Fig.7 Displacement time history of critical nodes

由图7可见，挡块的完全失效会引起梁体和索塔塔顶很大的侧向位移，如北仑侧的塔顶最大位移达到111 cm，梁端最大侧移量达到64 cm。这些位移会导致地震后结构空间形态上的很大残余变形，且在强震作用下，尤其是持时较长的地震动，梁体的这种大幅度的频繁的横向摆动所导致的拉索疲劳以及结构的整体稳定性问题是不可预知的隐患。

3 抗震对策探讨

按照前文的分析，无论横向约束体系如何变化，索塔的地震响应变化幅值不大，而且对于斜拉桥的横向抗震设计而言，锚墩往往是抗震薄弱环节［6］。设计中采用挡块限位措施对强地震作用下锚墩和边墩的受力具备有益的影响，尤其是在摩擦和碰撞效应的共同作用下。当然如何最有效地利用碰撞效应，如在梁体与限位挡块间加设高阻尼橡胶缓冲器［9］以降低碰撞力；挡块与梁体间合理的预留间隙等有待进一步的研究。从本文的分析结果来看，若采用钢筋混凝土挡块来实现约束梁体的目的有设计和实践上的困难（剪力需求过大，挡块尺寸有限），而一旦挡块失去限位功能，从图6可以看到梁体将发生很大的侧向变形，因此采用钢挡块或其它材料和形式的挡块来增强其抗剪强度是有效的抗震对策之一。此外，还可以通过阻尼器来实现斜拉桥横向抗震体系的优化问题。由于索塔纵向已布置液压粘滞阻尼器，为了避免其构造过于复杂，本文分别对边墩、锚墩单独设置和边墩、锚墩共同设置粘滞阻尼器三种情形进行分析。

表3 关键构件最大内力响应（设置阻尼器）Tab.3 Maximum internal forces of critical components with dampers being used

表4 关键构件最大位移响应Tab.4 Maximum displacement of critical components

由表3可见，在边墩处设置横向粘滞阻尼器可能有效地降低索塔和锚墩的地震响应；在锚墩处设置阻尼器对锚墩自身的受力非常有利，但对其余构件影响不大；在边墩和锚墩处均设置阻尼器，可以改善锚墩的地震反应，对索塔和边墩的受力也有一定程度的有利影响。但从表4的位移结果可以发现，欲使大榭主桥结构的支座在强震中免于破坏唯有在边墩和锚墩处都设置阻尼常数为5 000以上的大吨位液压粘滞阻尼器。显然，墩顶的狭小范围对设置大吨位阻尼器会造成设计和施工上的困难，而且从经济角度出发，设置具备足够强度的挡块限位装置也是更明智的选择。

4 结论

本文结合宁波大榭第二大桥，采用非线性时程分析法探讨了限位挡块对斜拉桥横向抗震体系的影响，主要结论如下：

（1）斜拉桥横向抗震分析中忽略挡块的作用会导致控制横向抗震设计的锚墩的响应被高估，而且容易导致固定支座的抗剪强度和活动支座位移能力的不足。

（2）考虑挡块的作用并在主梁与挡块之间设置一定的间隙可以有效地改善锚墩的地震响应，大幅降低设计成本；且碰撞效应不仅可以限制梁体侧向位移还能使结构由于刚度不对称所导致的受力不均现象得以缓解。

（3）强震下挡块的剪坏会引起梁体和索塔过大的侧向位移从而使结构在震后产生很大的残余变形，甚至由此导致结构稳定和拉索疲劳等问题。

（4）改善斜拉桥横向抗震体系可以通过在边墩和锚墩处设置阻尼器来实现，但可能会付出经济上的代价以及造成设计上的困难，而提高挡块的强度使其免于剪断对改善结构地震响应和减低设计造价而言是相对更好的选择。

［1］ Virlogeux M.Recent evolution of cable-stayed bridges［J］.Engineering Structures，1999，21：737 －755.

［2］叶爱君，范立础.附加阻尼器对超大跨度斜拉桥的减震效果［J］.同济大学学报（自然科学版），2006，34（7）：859－863.

［3］彭 伟，彭天波，李建中.多塔斜拉桥纵向约束体系研究［J］.同济大学学报（自然科学版），2009，37（8）：1003－1009.

［4］叶爱君，范立础.超大跨度斜拉桥的横向约束体系［J］.中国公路学报，2007，20（2）：63 －67.

［5］杨玉民，袁万城，范立础.大跨斜拉桥横向地震反应及其分形特征［J］.同济大学学报，2001，29（1）：15－19.

［6］王彬彬.大跨度斜拉桥和引桥的地震动耦联性分析研究［D］.上海：同济大学桥梁工程系，2007.

［7］范立础.桥梁抗震［M］.上海：同济大学出版社，1997.

［8］ Maleki S.Effect of side retainers on seismic response of bridges with elastomeric bearings［J］.Journal of Bridge Engineering，2004，9（1）：95 －100.

［9］ Jankowski R，Wilde K，Fujino Z.Reduction of pounding effects in elevated bridges during earthquakes［J］.Earthquake Engineering and Structural Dynamics，2000，29：195－212.

［10］ Kim S H，Mha H S，Lee S W.Effects of bearing damage upon seismic behaviors ofa multi-span girderbridge［J］.Engineering Structures，2006，28：1071 －1080.