高斯迷向凸体

王 雷， 何斌吾

(上海大学理学院，上海200444)

若在n维欧氏空间Rn中，体积(Lebesgue测度)为1、质心在原点的凸体K，对任意转轴都有相同的惯量矩，即对任意的单位向量θ，存在常数LK＞0，使得

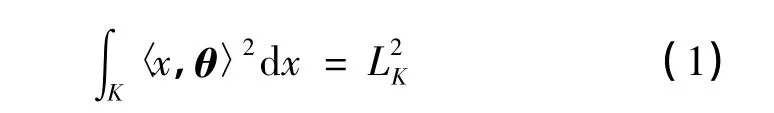
成立，则称凸体K处于迷向位置，常数LK称为凸体K在Lebesgue意义下的迷向常数［1］.近年来，许多学者对迷向凸体做了大量的研究工作［2-9］.一个很自然的问题是：若把式(1)左端积分换为高斯测度，情况又会怎么样呢?基于此，本工作给出高斯测度下迷向凸体的定义，并讨论其迷向条件的等价性以及球体和方体的迷向常数随维数变化的规律.

Rn中凸体K的标准高斯测度定义为

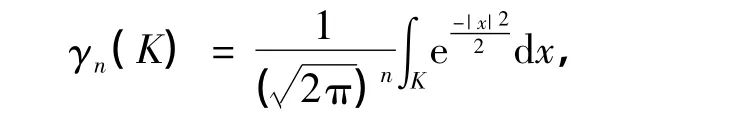
定义1 设K是Rn中的一个体积(Lebesgue测度)为1、质心在原点的凸体，令

如果K1满足

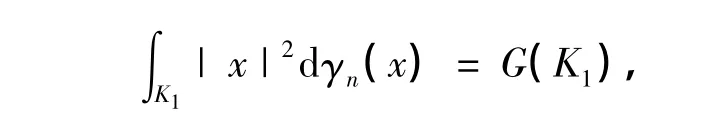
则称凸体K1为高斯迷向体.再令

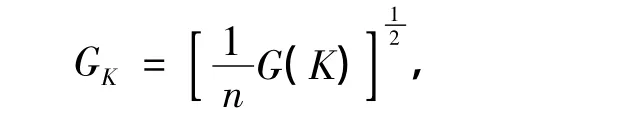
常数GK称为凸体K的高斯迷向常数.

本工作首先利用正定算子具有正方根的事实，证明高斯迷向体的存在性和正交不变性;其次，利用与Lebesgue等价性类似的方法证明高斯迷向体迷向条件的等价性;最后，计算超球体和超立方体的高斯迷向常数，并揭示高斯迷向常数与Lebesgue迷向常数不一样的性质.

1 高斯迷向体的存在性与正交不变性

定理1 设K是Rn中的一个体积(Lebesgue测度)为1、质心在原点的凸体，则存在T∈SL(n)，使得T(K)是高斯迷向的，并且这种高斯迷向体在正交变换下是不变的，即若K1是K的高斯迷向体，则K2是K1经正交变换T∈O(n)所得凸体，K2也是K的高斯迷向体.

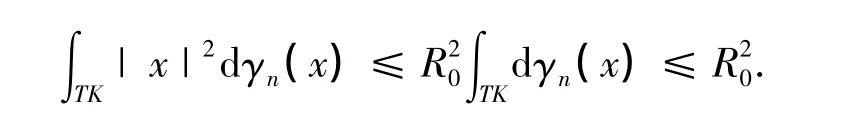
式(2)中的上确界是对T∈SL(n)取的，又因SL(n)是保体积变换的集合，它在矩阵范数下为一个紧集，从而此积分的上确界是可以达到的，因此，存在T0，满足

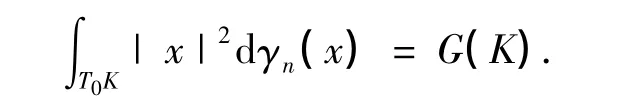
下面证明高斯迷向体的正交不变性.设K1是K的高斯迷向体，K2是K1经正交变换所得的凸体，即K2=TK1，T∈O(n)，可推理如下：

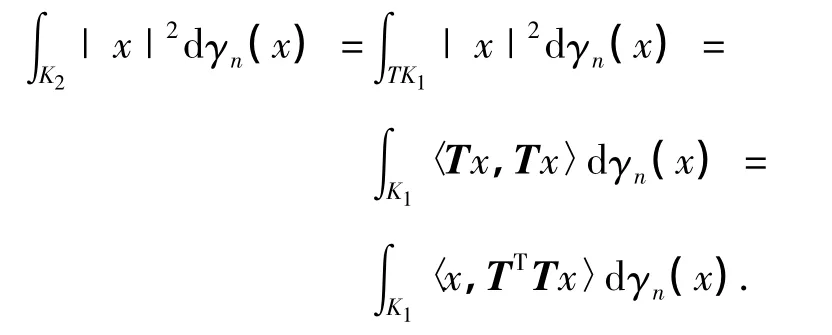
又因T为正交变换，所以，TTT=I(单位矩阵)，因此，正交变换条件下高斯迷向凸体具有正交不变性.定理得证.

2 高斯迷向条件的等价性

传统意义的Lebesgue迷向条件具有等价性.定义高斯迷向凸体后，一个很显然的问题是：高斯迷向条件是否存在类似Lebesgue迷向条件的等价性?依据上述猜测，下面给出高斯迷向条件的等价性证明.

定理2 Rn中体积(Lebesgue测度)为1、质心在原点的高斯迷向凸体K满足下列条件，对于任意θ∈Sn-1，有

高斯迷向凸体K满足的条件式(3)等价于如下3个等式：

(i)对任意y∈Rn，有

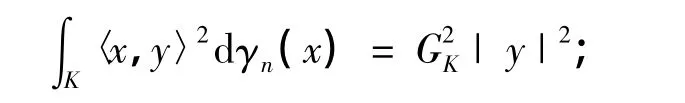
(ii)对任意i，j=1，2，…，n，有

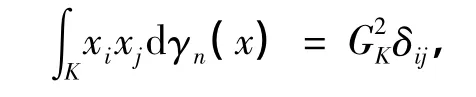
式中，x1，x2，…，xn是x对应于某组标准正交基的坐标，δij是Kronecker符号;

(iii)对任意T∈L(Rn)，有

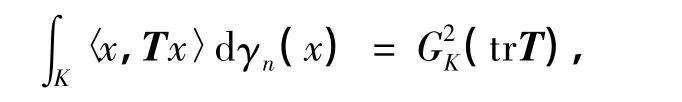
式中，trT是线性变换T的迹.

证明 首先论证(i)和式(3)的等价性.对任意y∈Rn，y≠0，令y=|y|θy，显然有

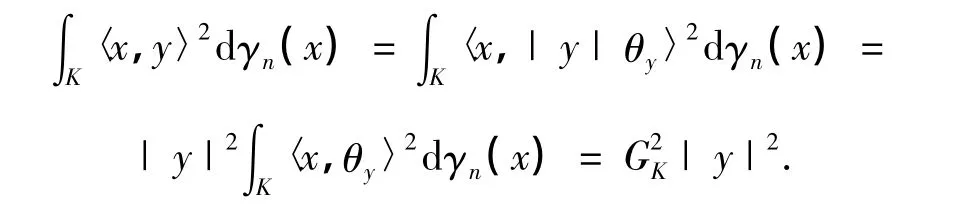
因为|y|2≠0，所以，∫K〈x，θy〉2dγn(x)=考虑到y是任意的，必要性(i)得证.充分性的证明相对简单，故略去.

其次，论证(i)和(ii)的等价性.不妨先证明高斯迷向凸体所满足式(3)和(ii)等价.

设e1，e2，…，en为Rn中的一组标准正交基，δij是Kronecker符号.取θ=ei(i=1，2，…，n)，则

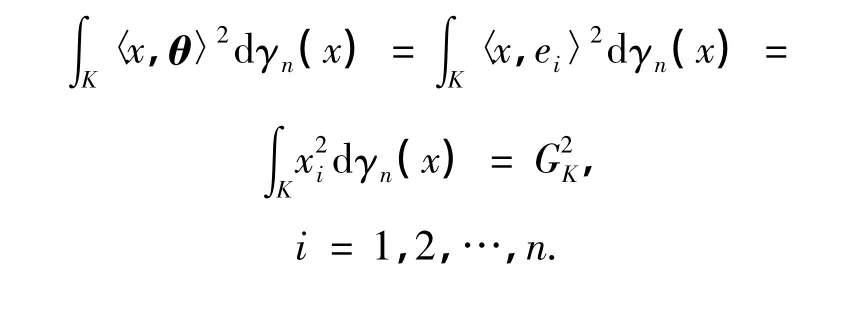
对任意i，j=1，2，…，n，i≠j，λμ≠0，且λ2+μ2=1，取θ=λei+μej，代入上式得

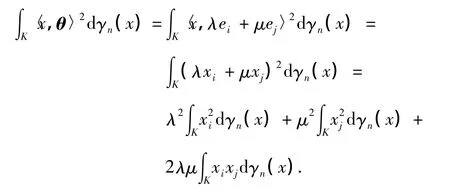
结合(i)，则有∫Kxixjdγn(x)=0，i≠j，i，j=1，2，…，n.比较等式两边，充分性得证.

对任意的θ∈Sn-1，令θ=λ1e1+…+λnen++…+=1，则有

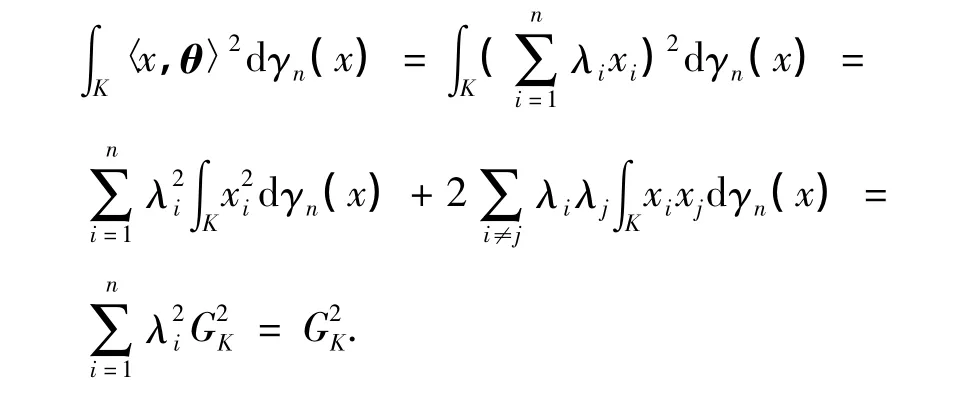
必要性得证.

证得式(3)和(ii)等价，依据等价条件具有传递性，证得(i)和(ii)具有等价性.

最后，论证(ii)和(iii)的等价性.

设T∈L(Rn)，其对应标准正交基e1，e2，…，en的矩阵为 T=(tij)n×n，从而 Tx的矩阵为 T(x1，x2，…，xn)T，因此，

由式(2)可得

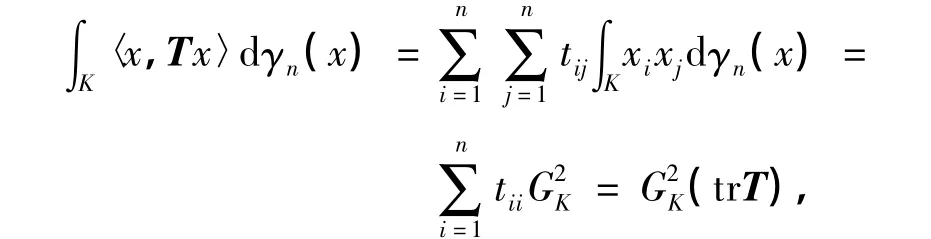
充分性得证.

同样，对于T∈L(Rn)，存在等式

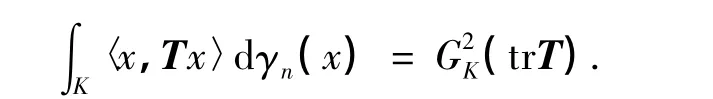
取Ti∈L(Rn)，使Ti在基e1，e2，…，en的矩阵为Eii，其中Eij表示i行j列上的元素为1、其余的元素为0的n阶方阵.

易知，Tix=xiei，trTi=1，i=1，2，…，n，

取Tij∈L(Rn)，使Tij在基e1，e2，…，en的矩阵为Eij+ Eji，i≠j(i，j=1，2，…，n)，其中Eij的表示同上.

对于 x=x1e1+… +xnen，有 Tijx=xiej+xjei，trTij=0，i≠j，

因此，∫Kxixjdγn(x)=0，必要性得证.

综上，定理2得证.

3 两类凸体的高斯迷向常数

根据高斯迷向凸体的迷向常数的定义，对n维空间中的球体和方体的高斯迷向常数进行计算.先计算球体的高斯迷向常数，

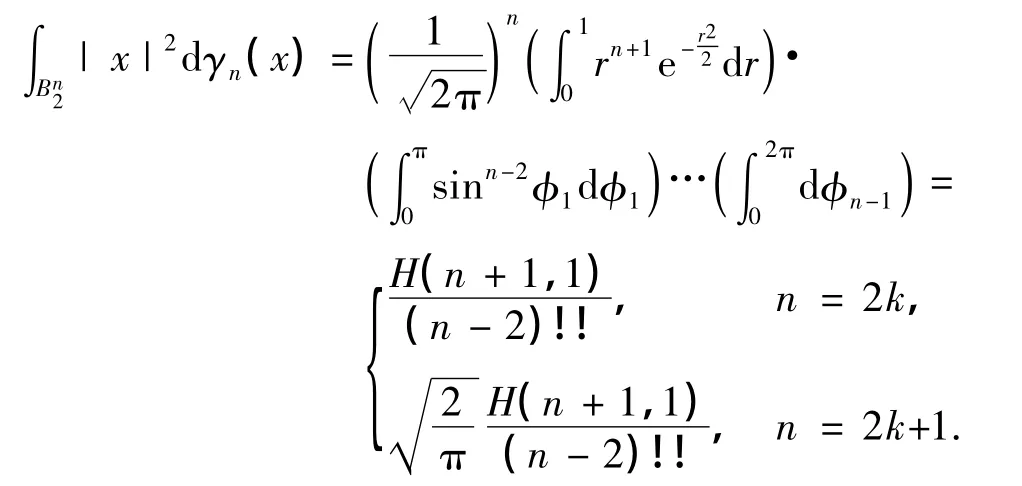
考虑到|rn|=1，而且

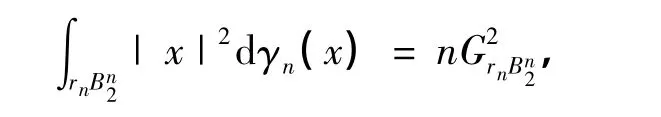
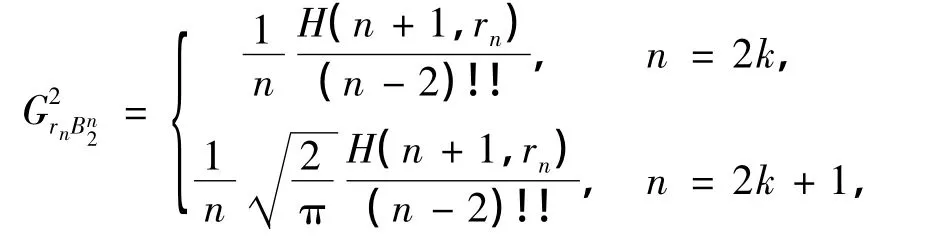
式中

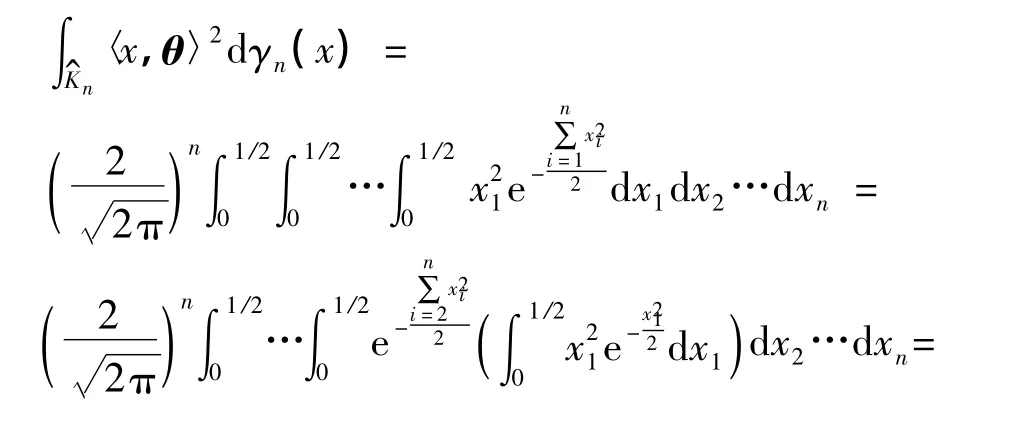
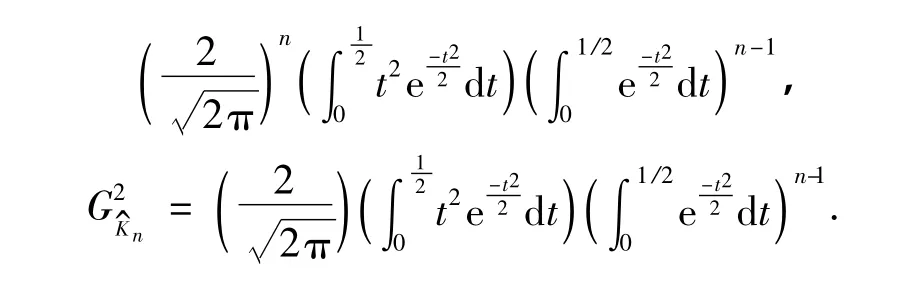
下面对单位体积的球体和方体的高斯迷向常数进行数值比较：

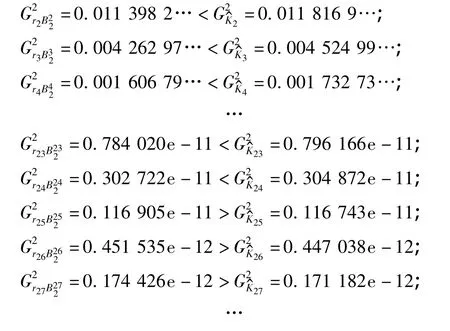
通过数值分析发现，在n≥25时，单位球体的迷向常数大于单位方体的迷向常数，这与Lebesgue测度下的情况恰恰相反.

［1］ MILMANV D，PAJORA.Isotropic position and inertia ellipsoilds and zonoids of the unit ball of a nomed ndimensionalspace［C］∥ Geometric Aspects of Functional Analysis(1987—1988)，Lecture Notes in Math 1376.Berlin：Springer，1989：64-104.

［2］ LUTWAKE，YANGD，ZHANGG Y.A new ellipsoid associated with convex bodies［J］.Duke Math J，2000，104(3)：375-390.

［3］ GIANNOPOULOSA.Notes on isotropic convex bodies［D］. Warsaw： Institute ofMathematics， Polish Academy of Sciences，2003：10-15.

［4］ SCHMUCKENSCHLAGERM.Volume of intersection and sections of the unit ball of［J］.Proc Amer Math Soc，1998，126：1527-1530.

［5］ GAOP.A note on the volume of section of［J］.Math Anal Appl，2007，326：632-640.

［6］ ALZERH.Inequalities for the volume of the unit ball in Rn［J］.Math Anal Appl，2000，136：353-363.

［7］ 何斌吾，冷岗松.迷向体与Bourgain问题［J］.中国科学：A辑，2005，35：450-462.

［8］ 吴力荣，何斌吾.几类特殊几何体的迷向常数［J］.上海大学学报：自然科学版，2007，13(1)：41-46.

［9］ 陈巧云，何斌吾.凸体迷向条件的等价性［J］.上海大学学报：自然科学版，2006，12(5)：481-483.