一类参数边界条件的奇异Stu rm－Liouville问题的自伴性

刘常凯，张茂柱

(泰山学院数学与系统科学学院，山东泰安 271021)

1 引言

边界条件中含有特征参数的Sturm－Liouville问题许多作者做了大量的研究(如参考文献［1－5］等)，这些文章主要讨论正则情形.对于奇异情形时两边界条件均含参数的Sturm－Liouville问题有较少的研究.本文考虑奇异Sturm－Liouville问题

参数边界条件为

2 主要结果

构造新的Hilbert空间H=L2(a，b)⊕C2，∀F，G∈H，F=(f(x)，f1，f2)T，G=(g(x)，g1，g2)T，定义H上的内积为

构造算子A为

引理1［6］

引理2［6］

定理1 算子A的定义域D(A)在H中稠.

证明:设F=(f(x)，f1，f2)T∈H，且F⊥D(A)，下证F=0.假设U=(u(x)，u1，u2)T，u(x)∈C0∞(a， b)，则U∈D(A)，并且F⊥U，即，因此f(x)在L2(a，b)中正交于C0∞(a，b)，故f(x)在区间(a，b)内几乎处处为0.假设V=(v(x)，v1，0)T∈D(A)，则.由于v1可以任意选取，故f1=0.同时f2=0.

定理2 算子A为H中的对称算子.

证明:对∀F，G∈H有

又因为u，v是实的，且［u，v］(a)=1.由引理1得

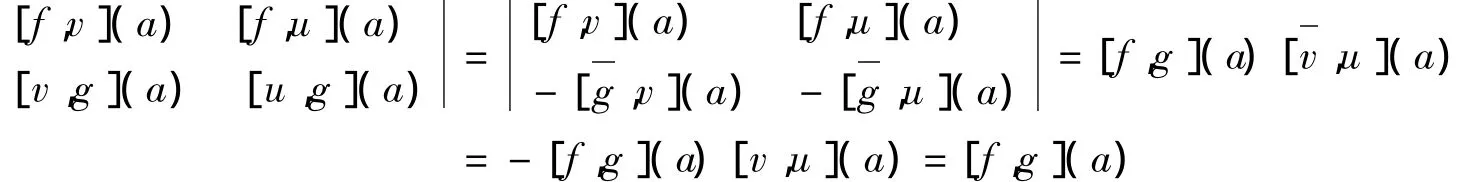
同理，［f，u］(b)［v，g］(b)－［f，v］(b)［u，g］(b)=－［f，g］(b).所以，(AF，G)－(F，AG)=0.

定理3 算子A为H中的自伴算子，并且算子A的特征值即为问题(1.1)－(1.3)的特征值.

证明:只需证明若对任何的F=(f(x)，f1，f2)T∈D(A)有(AF，G)=(F，W)成立，则

G∈D(A)且AG=W，其中G=(g(x)，g1，g2)T，W=(w(x)，w1，w2)T∈H，即

(1)g，g'∈ACloc(a，b)，lg∈L2(a，b)，lg=w;

(2)g1=a1［g，u］(a)，g2=a2［g，u］(b);

(3)－b1［g，u］(a)+［g，v］(a)=w1，－b2［g，u］(b)+［g，v］(b)=w2.

事实上，对任意的f(x)∈C∞0(a，b)，F=(f(x)，0，0)T∈D(A)，由(AF，G)=(F，W)得到由标准的Sturm－Liouville理论(1)成立.下证(2)、(3)成立.由(AF，G)=(F，W)可得

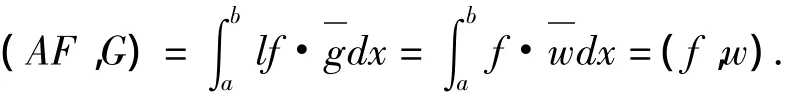
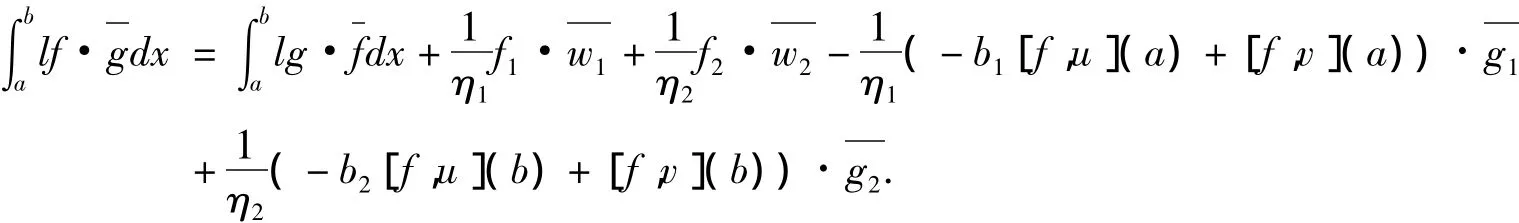
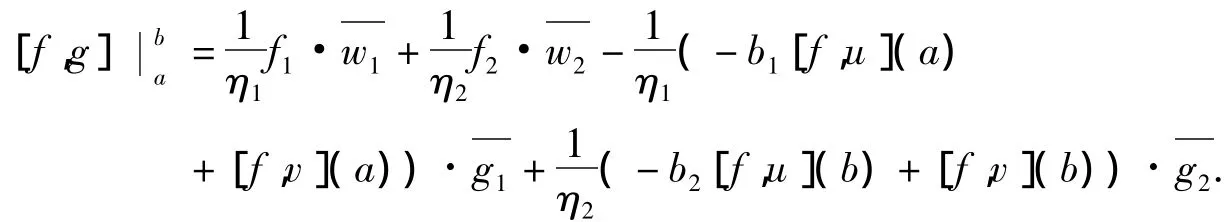
由引理2，存在f使得［f，u］(a)=0，［f，v］(a)=1，［f，u］(b)=［f，v］(b)=0.

由引理1结合上式可得g1=a1［g，u］(a).同理也存在f使得

［f，u］(a)=1，［f，v］(a)=0，［f，u］(b)=［f，v］(b)=0.

由引理1结合g1=a1［g，u］(a)可得－b1［g，u］(a)+［g，v］(a)=w1.同理可证(2)(3)的其余部分成立.

［1］Johann Walter.Regular eigenvalue problemswith eigenvalue parameter in the boundary conditions［J］.Math.Z.，1973，(133):301－312.

［2］C.T.Fulton.Two－piont boundary value problems with eigenvalue parameter contained in the boundary conditions［J］.Proc.Roy.Soc.Edinburgh，1977，(77A):293－308.

［3］P.A.Binding，P.J.Browne，K.Seddighi.Sturm－Liouville problems with eigenparameter dependent boundary conditions［J］.Proc.Edinburgh.Math.Soc.，1993，37(2):57－72.

［4］P.A.Binding，P.J.Browne，B.A.Watson.Equivalence of inverse Sturm－Liouville problems with boundary conditions rationally dependent on the eigenparameter［J］.J.Math.Anal.Appl.，2004，(291):246－261.

［5］Jussi Behrndt，Carsten Trunk.Sturm－Liouville operatorswith indefinite weight functions and eigenvalue depending boundary conditions［J］.J.Differential Equations，2006，(222):297–324.

［6］A.Zettl.Sturm–Liouville Theory［J］.American Mathematical Society，Mathematical Surveys and Monographs，2005，(121).