“数字信号处理”中分段卷积的教学探讨

栗学丽,刘 琚

(山东大学信息科学与工程学院,山东济南 250100）

“数字信号处理”中分段卷积的教学探讨

栗学丽,刘 琚

(山东大学信息科学与工程学院,山东济南 250100）

本文对“数字信号处理”课程中难以理解的分段卷积进行解析,并对使用中常见问题进行解答。重叠相加法和重叠保留法是分段卷积的两种易混淆方法,通过举例法、质疑法和实践法等多种教学方法对它们进行分析比较,说明它们的用法,加深概念的理解,以达到学以致用的目的。

数字信号处理;分段卷积;重叠相加法;重叠保留法

分段卷积是“数字信号处理”课程中重要的应用和难点之一,它采用两种方法实现,即重叠相加法和重叠保留法。教科书中一般都给出这两种方法的原理和公式,或给出图示解释[1]。但是,我们发现,多数学生对这两种方法不能很好地理解,也不会实际运用。本文利用Matlab GUI制作出交互式动画课件辅助教学,把抽象的概念形象化。

1 重叠相加法和重叠保留法

对于很长序列和短序列的卷积,可采用重叠相加法和重叠保留法进行快速分段实现。设单位冲激响应h(n)的点数为M,输入信号x(n)为很长的序列。

重叠相加法是将长序列x(n)分解为若干段,每段xi(n)长度为L(L和M为同一数量级)。将xi(n)和h(n)补零到N点(N≥L+M-1),用圆周卷积得到每段线性卷积的值。由于整个卷积值等于各分段卷积值之和,所以将相邻两段输出序列的重叠区(M-1点)相加就得到正确值。

重叠保留法也是将长序列 x(n)分解为若干段xi(n),但每相邻段重叠M-1点(对第一段采取前面补M-1个零值),使得每段长度为N点,做N点的x i(n)和h(n)圆周卷积。由于每段圆周卷积结果的前M-1点不等于线性卷积值,故将每段输出结果的前M-1点去掉,剩下的点连结起来就是正确值[1]。

具体的证明公式见参考文献[1],这里不再赘述。现就用举例法、质疑法和实践法说明它们的用法。

2 举例法

解法2:重叠相加法

已知 M=3,令L=5,将 x(n)分段,得

与直接卷积法结果比较,会发现y1尾部和y2头部的M-1=2点值不对,而将y1尾部和y2头部值重叠M-1点值相加,得到y(n)={1 2 2 2 2 2 2 2 2 2-9-10}。此值与直接法比较,两者相等,说明此法正确。

解法3:重叠保留法

由重叠相加法可知,分段卷积结果每段前M-1点值不等于线性卷积值,所以要去除。同时,为了保证各段卷积滤波结果的连续性,每段输入需要重叠M-1点,即为重叠保留法。

已知M=3,将x(n)重叠M-1=2点分段,每段长度为5,得x1(n)={0 0 1 2 3},x2(n)={2 3 4 5 6},x3(n)={5 6 7 8 9},x4(n)={8 9 10 0 0}。

将每段与h(n)做N=5的圆周卷积,得

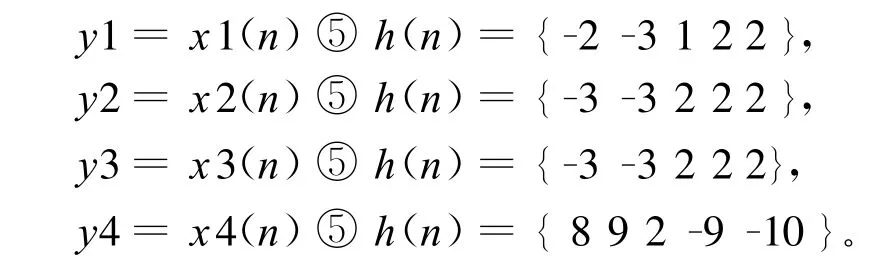
由于每段圆周卷积结果的前M-1点不等于线性卷积值,故每段输出去掉前M-1点,将剩下值连接起来,得到y(n)={1 2 2 2 2 2 2 2 2 2-9-10}。可见与直接法的结果相同。

已知x(n)=(n+1),0≤n≤9,h(n)={1,0,-1},分别用直接法、重叠相加法和重叠保留法求解 x(n)＊h(n)。

解法1:直接法

通过卷积公式可知

通过这一个简单的例题,用三种方法求解,比较它们的使用方法,使学生对这三种方法有了直观的理解。

3 质疑法

质疑法是对理论的进一步深化,教师提出问题,启发学生思考,加深概念的理解。

疑问1:既然重叠保留法前M-1点不正确而要去除,能否分段时重叠处直接补零,运算是否会简单?

现在我们就如此分段:

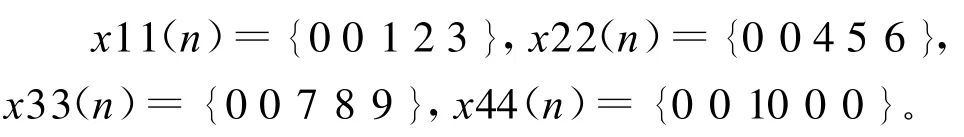
下面的求解过程同上,得到结果为{1 2 2 4 5 2 7 8 2 10 0-10},可见与 x(n)＊h(n)值不相等。那为什么必须要保留前段的M-1个数据,而不能直接补上M-1个零值呢?启发学生考虑因果系统的性质。如果因果系统的单位冲激响应h(n)是长度为M的序列,则当前的输出不仅取决于当前的输入,而且还取决于以前的M-1个输入。这样,在计算n时刻的卷积值时,就不仅与n时刻的输入样值有关,而且还与n时刻以前的M-1个样值有关。所以,必需将前段输入序列的后M-1个点保留在本段序列之前,即每段输入要重叠M-1点,方可将前段对本段的影响考虑进去,这样才不会造成输出信号的遗漏,得出正确值。

疑问2:如果不是进行N点的圆周卷积,而是将每段后面补零到2的整数幂,便于通过 N 2点的FFT实现。这样,每段得到N2个点值,是不是仅需要每段去掉前M-1个点就可正确相连呢?

上题令N2=8,利用FFT进行圆周卷积,得:

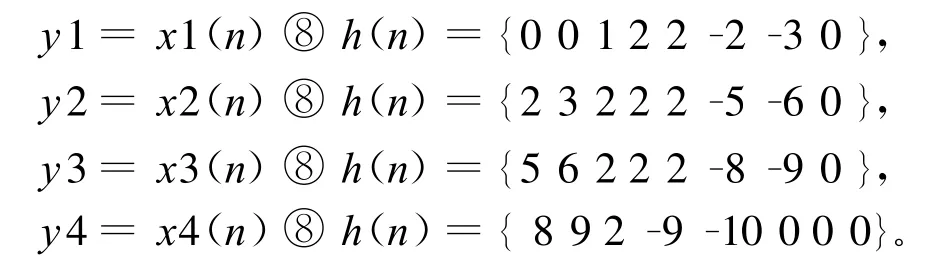
可见,正确的结果应是每段去掉前M-1个点,以及后N2-N个点,即将中间的第M点到第N点作为正确结果连接起来。所以严格的说,重叠保留法是将每段输出结果第M点到第N点连接起来得到正确值。

疑问3:此处重叠相加法与语音信号处理中讲解的重叠相加法OLA(OverLap-Add method)[3]进行语音合成是不是同一个概念?

语音信号是长时信号,它表现出短时平稳性,所以一般是采用重叠加窗分帧,也就是分段时有重叠,每段信号乘上Hamming窗或Hanning窗,然后分析得到每帧的特征参量,对特征参量进行分析、编码、合成、识别等处理。若需要得到处理后的语音,合成时对每帧信号重叠区进行相加,即重叠相加法实现,有时也翻译为叠接相加法。

由此可见,语音信号处理中讲解的重叠相加法(分段时重叠)与我们数字信号处理讲解的重叠相加法(分段时不重叠)是不同的概念,名称相同,物理概念不同。数字信号处理讲解的重叠相加法是实现分段卷积,语音信号处理中讲解的重叠相加法是为了合成时去除加窗的影响。学生一旦理解了物理概念,就不会混淆了,才能正确运用。

4 实践法

我们利用Matlab GUI设计了一个分段卷积的交互式动态演示系统,图1和图2分别给出了实现重叠相加法和重叠保留法的一个动态演示界面。

我们以图1为例来解释该系统的用法。该系统具有交互功能,通过更改界面左侧的输入信号、单位冲激响应和分段的长度,便可观察到相应的图形变化。界面的中部给出所选方法的图示。界面的右侧给出五个子图形,从上到下分别对应着输入信号、单位冲激响应、输入信号的每一子段、相应的中间输出值及最终的输出结果的波形。图中还给出了动态显示分段卷积过程的中间输出值。我们可以选择输入信号为实际的语音信号,单位冲激响应选择低通滤波器,通过选择不同的实现方法,以实时可变的动态图形展示给学生。我们可以看到这三种方法实现过程不同,所用时间不同,但是滤波的结果一致的,确实得到的是低频信号。使学生对滤波的概念有更清楚的认识。

可见通过操作交互式动态演示系统,既能直观验证原理方法的正确性,又可加深学生对所学知识的理解。此外,我们还给出最新的分段卷积的研究成果链接,学生可以自主学习,或编程实现课堂上讲授的相关知识内容,从而提高学生的分析问题能力和实际动手能力。

5 结语

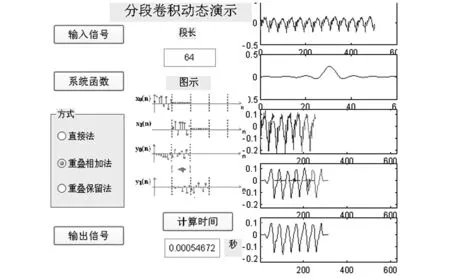
图1 重叠相加法实现过程图解

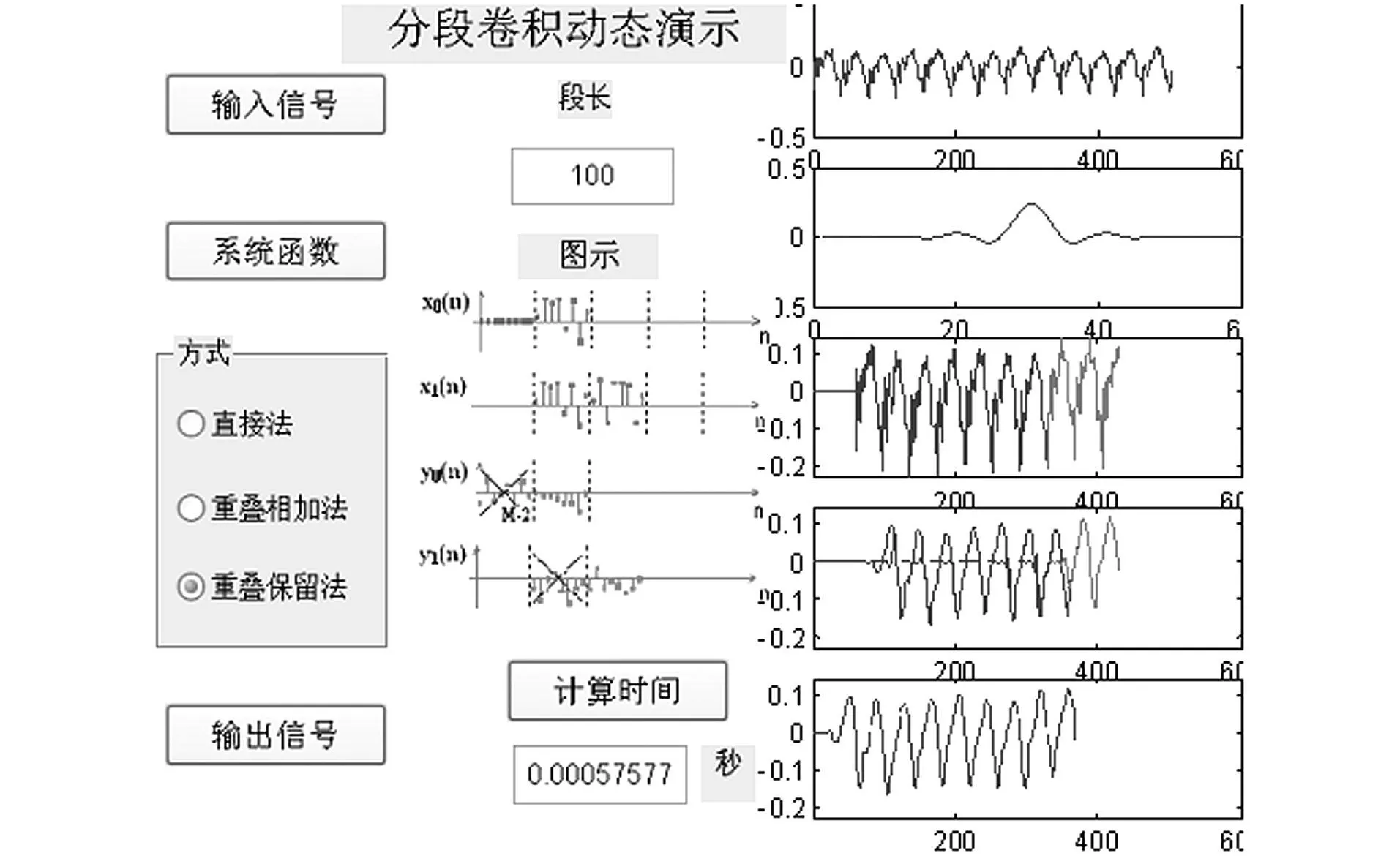
图2 重叠保留法实现过程图解

如何帮助学生理解与掌握“数字信号处理”课程中的基本概念、基本原理、基本分析方法以及如何提高其综合应用所学知识解决实际问题的能力,是本课程教学中所要解决的关键问题[5]。

本文通过举例法和质疑法实例讲解分段卷积中重叠相加法和重叠保留法的用法,加上采用Matlab实践应用,来帮助学生理解和应用。举例法有利于得到直观认识,质疑法有利于激励创新精神,实践法有利于倡导活学活用。这三种方法虽并非新方法,但是我们将它们有机的结合,在讲述分段卷积的概念和用法上对教科书给予很好的补充,取得了较好的教学效果。

[1] 程佩青.数字信号处理教程[M].北京:清华大学出版社,2007

[2] V inay K.Ingle,etc.Digital Signal Processing U sing Matlab(影印本)[M].北京:科学出版社,2003

[3] Thomas F.Quatieri.Discrete-Time Speech Signal Processing:Principlesand Practice[M].New Jersey:Prentice HallPTR,2002

[4] 姚秀芳,崔松菲.基于MA TLAB GUIDE的程序设计[J].合肥:电脑知识与技术,2009,5(27):7767-7768

[5] 栗学丽,刘琚.讨论“数字信号处理”教学中易混淆的问题[J].南京:电气电子教学学报,2009,31(4):39-41

Teaching Methods and Analysis of Block Convolution in Digital Signal Processing

LIXue-li,LIU Ju

(Schoolo f In formation Science and Engineering,Shandong Univ.,Jinan 250100,China)

Block convolution is one of the difficulties in the course of Digital Signal Processing.In this paper,the concep t of b lock convolution is analyzed and some frequently asked questions are interp reted.Through several teachingmethods,i.e.the examp ling method,the questioning method and the practicing method,the con fusab lemeans of the overlap-add method and the overlap-savemethod for the block convolution are analyzed com paratively and explained their usage.It is help ful for the students to understand and app ly.

digital signal p rocessing;b lock convo lution;overlap-add method;overlap-savem ethod

TN911.72;G642

A

1008-0686(2011)02-0102-03

2010-07-01;

2010-12-23 基金项目:山东大学2009年教学改革项目(山大教字〔2010〕13号)

栗学丽(1972-),女,博士,副教授,主要从事数字信号处理方面的教学和科研,E-mail:lixueli@sdu.edu.cn

刘 琚(1965-),男,博士,教授,主要从事数字信号处理和通信方面的教学和科研。