《数字信号处理》中存在的难点问题解析
王海鹏 丛瑜 王萌
摘要:《数字信号处理》这门课程中,概念多,公式复杂,许多难点问题成为了学生学习过程中的绊脚石,如线性卷积、周期卷积和圆周卷积的概念,三种傅里叶变换的概念及相互之间的关系等。本文在具备大量教学经验基础上,针对难点问题进行解析,让学生能够理清思路,拨开云雾,以此激发学生的积极性。
关键词:数字信号处理; 卷积; 傅里叶变换
中图分类号:G434文献标志码:A文章编号:2095-9214(2016)12-0083-02
数字信号处理[1]作为信息处理、电子工程等专业的专业基础课程,有很强的理论性和实践性,对于学生从事电子类的工作和继续深造电子信息类专业,都有不可低估的基石作用。但是由于这门课程公式繁杂、理论性强、很抽象,所以学生在学习过程中显得有些力不从心。为了能够解决学生在学习中普遍遇到的一些难点问题,本文做了详细的解析。
一、线性卷积、周期卷积和圆周卷积
卷积[2]是数学运算中的一种重要运算,也是信号处理中的一个重要理论。在线性系统中,如果输入信号是x(n),系统的冲激响应是h(n),则输出信号为x(n)和h(n)的卷积。卷积描述了信号通过系统后的变换,反映了线性时不变系统中输入和输出的关系,但是在数字信号处理中出现了三种卷积,线性卷积、周期卷积和圆周卷积,这三种卷积往往使学生感到很迷惑,容易混淆。
线性卷积:y(n)=x(n)h(n),x(n)的长度为N1,h(n)的长度为N2;
周期卷积:(n)=(n)(n),(n)和(n) 的周期为N ;
圆周卷积:y(n)=x(n)h(n),x(n) 和 h(n)的长度均为N,不足者补零。
首先三种卷积针对的对象不同,线性卷积针对的序列x(n)和h(n)是任意的两个序列,而周期卷积针对的是两个周期序列和,而且周期同样都为N。圆周卷积针对的对象是有限长序列(n) 和(n),而且圆周卷积和周期卷积没有本质的区别,它和周期卷积的过程是一样的,只不过结果只取了主值区间而已。其次三种卷积后的序列的长度有所不同。假设输入序列x(n) 的长度为 N1,h(n)的长度为N2,则线性卷积后序列的长度L为N1+N2-1。周期卷积后的序列依然是一个周期序列,而且周期跟输入序列的周期一样都为N。圆周卷积后序列的长度也为N,注意这里的N是周期序列的周期,N可能大于L,也可能小于L。当N≥L时,线性卷积和圆周卷积的结果是一样的,当N≤L时,N点的圆周卷积是线性卷积的结果以N点为周期的周期延拓序列的主值序列。如果学生能够从这两个方面对三种卷积进行比较的进行学习,将会使得对问题的理解更容易些。
二、离散时间傅里叶变换(DTFT)、离散傅里叶级数(DFS)和离散傅里叶变换(DFT)
在教学过程中,需要对学生强调的是,本门课程的重点是离散傅里叶变换。DTFT和DFS实际上是学习DFT之前的预备知识,DFT才是数字信号处理的核心知识。所以在学习过程中,一定要遵循既要相互区别又要相互联系的学习方法,才能真正地理解所学知识点[3]。
傅里叶变换是法国数学家和物理学家傅里叶在1807年发表了一篇论文,提出任何连续周期信号的都可以由一组适当的正弦曲线组合而成,从而开辟了分析信号的另一个领域——频域。傅里叶变换显然是时域和频域的对应关系,在理解DTFT、DFS和DFT时,显然要弄清楚这三种变换在时域和频域的相同点与不同点。
首先在时域上,离散时间傅里叶变换(DTFT)的研究对象是任意一个序列,例如正弦序列,离散傅里叶级数(DFS)研究的对象是周期序列,如复指数序列ejωn,而离散傅里叶变换(DFT)的研究对象是有限长的序列,如矩形序列RN(n)。
其次在频域上,离散时间傅里叶变换的频谱是连续且周期的函数,周期为2π。傅里叶技术的频谱是离散且周期的函数,周期为N。离散傅里叶变换的频谱是离散且非周期的,长度为N。
在区别DFS和DFT的时候,一定要记住,DFS和DFT没有本质的区别,DFT只不过是时域和频域均取了一个周期的值而已。在DTFT和DFT的区别中,DFT是DTFT进行离散化后的取值。
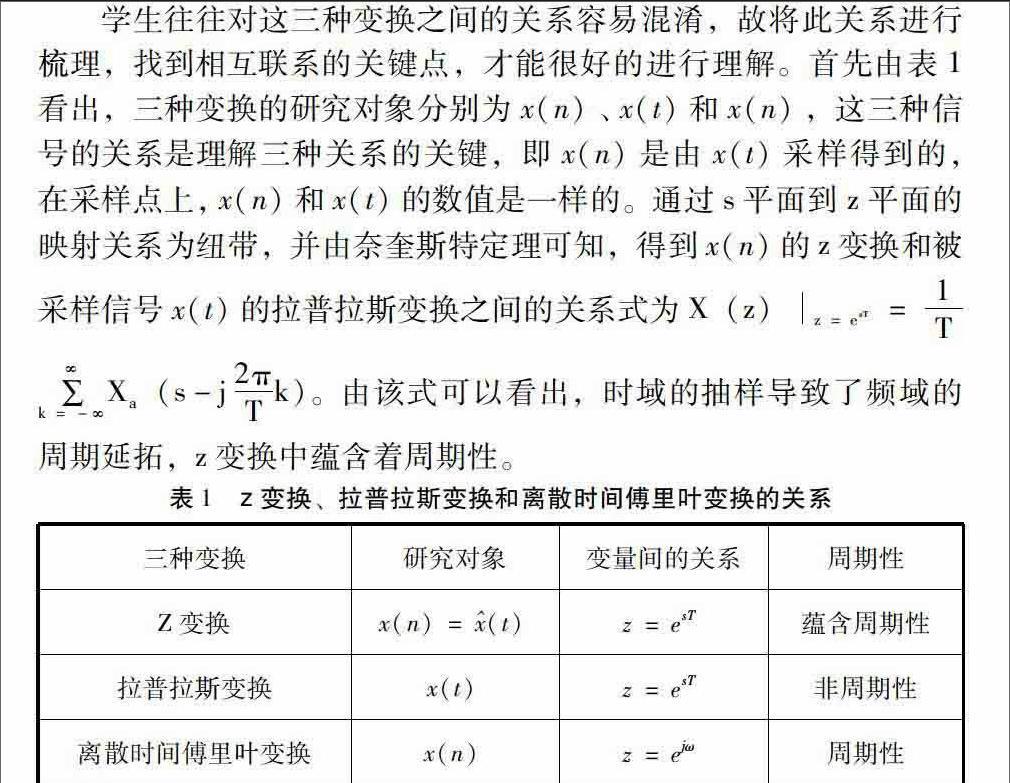
三、z变换、拉普拉斯变换和离散时间傅里叶变换
z变换在离散时间系统中的作用如同拉普拉斯变换在连续时间系统中的作用一样,它把描述离散系统的差分方程转化为简单的代数方程,使得求解大大的简化。由于数字信号是又连续时间信号采样得到的,故数字信号的z变换与被采样的连续信号的拉普拉斯变换有密切关系。
学生往往对这三种变换之间的关系容易混淆,故将此关系进行梳理,找到相互联系的关键点,才能很好的进行理解。首先由表1看出,三种变换的研究对象分别为x(n)、x(t)和x(n),这三种信号的关系是理解三种关系的关键,即x(n) 是由x(t)采样得到的,在采样点上,x(n)和x(t)的数值是一样的。通过s平面到z平面的映射关系为纽带,并由奈奎斯特定理可知,得到x(n)的z变换和被采样信号x(t)的拉普拉斯变换之间的关系式为X(z)z = esT = 1T∑∞k = -∞Xa (s-j2πTk)。由该式可以看出,时域的抽样导致了频域的周期延拓,z变换中蕴含着周期性。
由表1第二列的关系式 z=ejω可以看出,序列在单位圆上的z变换,就是序列的离散时间傅里叶变换。
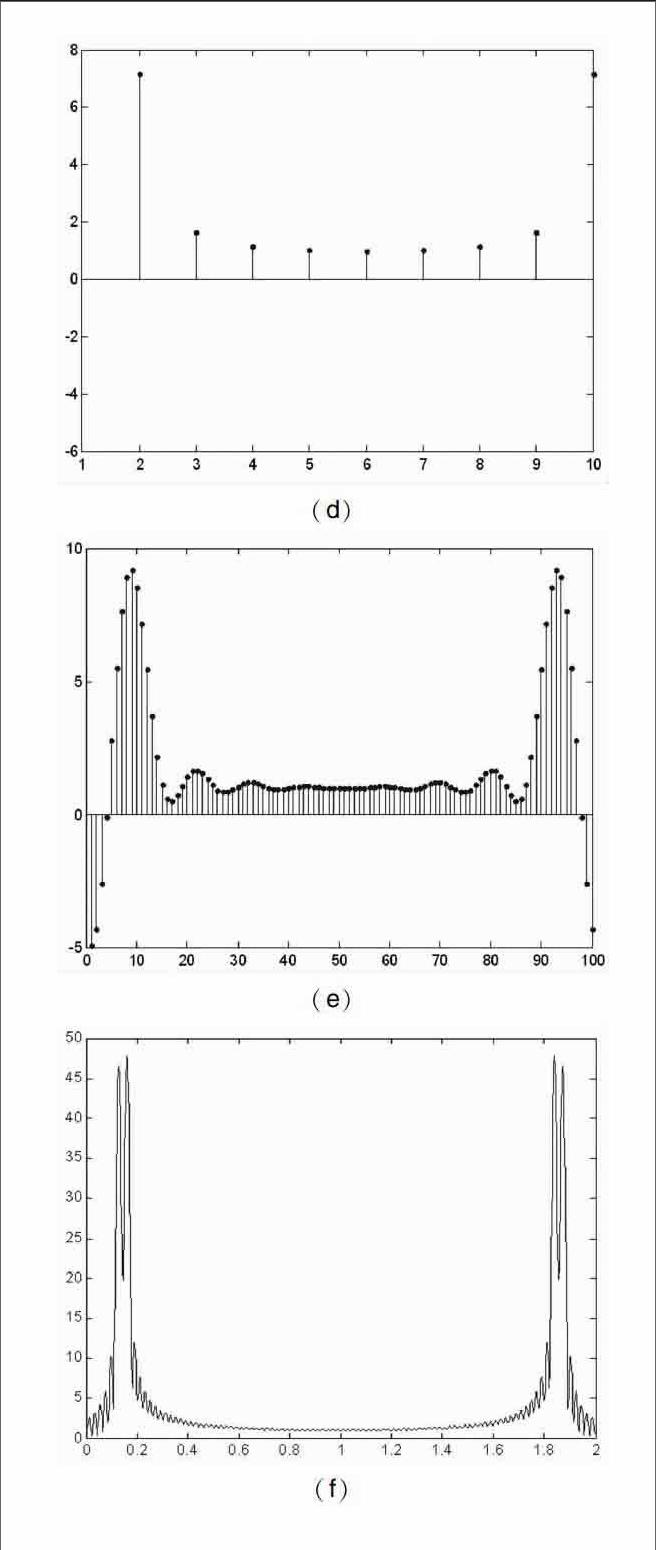
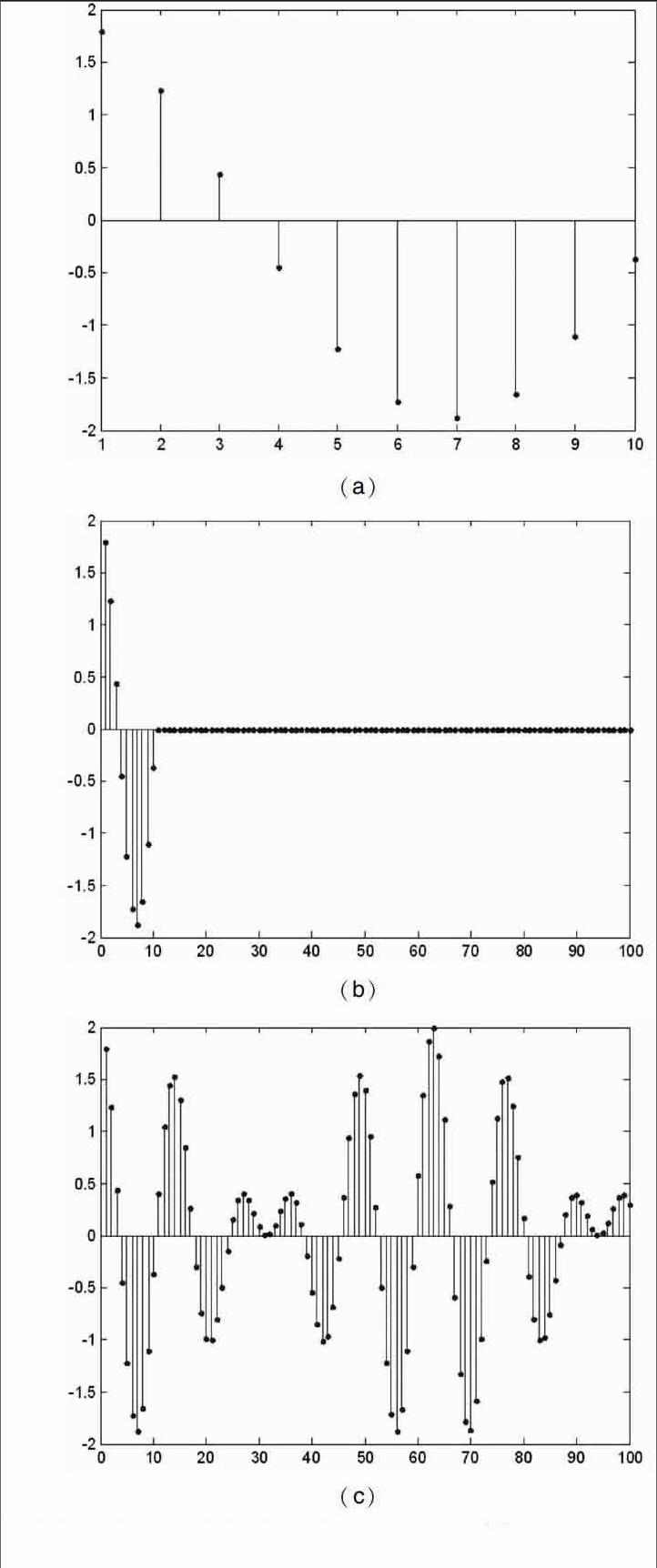
四、高密度谱和高分辨谱[4]
在分析数字信号的频谱时,我们往往很关心信号的频率分辨力,对于信号x(n),n1≤n≤n2,信号的长度为T0,如果想提高信号的频率分辨力,必须增加信号的有效长度,使得信号的长度 TT0,如果通过在信号x(n)后补零来增加信号的长度,是不会增加频率分辨力的。这个问题给历届学生带来过困惑,很多学生会认为,补零后增加了信号的长度,也就提高了信号的频率分辨力,这其实是错误的。补零后只会使得信号的谱线更加平滑,即得到高密度谱,而不会增加信号的任何信息,从而不会提高频率分辨力。
图(d)和(e)只显示了一个峰值,(e)较(d)更平滑,即补零使得谱线显得更加平滑,消除了栅栏效应,但是无法分辨出更多的谱线。(f)中则出现了两条谱线,即能够将信号中的两个频率成分分辨出来,从而说明增加信号的有效长度,能够提高信号的频率分辨力。
结束语
本文所述四个问题,均为上课过程中学生所普遍遇到的难点问题,这些问题如同前进大道上的沟沟坎坎,容易让学生陷进去出不来,如果能够将这些问题迎刃而解,在学习数字信号处理这门课的过程中,思路将更加清晰明了,不仅能够加深学生对知识的理解,提高学生解决问题的能力,而且能激发学生对学习的积极性和创造力。
(作者单位:海军航空工程学院信息融合研究所)
参考文献:
[1]程佩青.数字信号处理教程(第四版).清华大学出版社,2013.08.
[2]于家诚.数字信号处理课程教学中需要解决的几大关系.合肥师范学院学报,2009.05,第27卷第3期
[3]耶晓东.数字信号处理课程兴趣教学法初探.高教论坛,2011.01第一期.
[4]栗学丽,刘琚.数字信号处理_教学中易混淆的问题讨论.电气电子教学学报,2009.08,第31卷第4期