密勒定理及其应用

田社平,陈洪亮

(上海交通大学电子信息学院,上海 200240）

密勒定理及其应用

田社平,陈洪亮

(上海交通大学电子信息学院,上海 200240）

密勒定理在电路分析和设计中具有较广泛的应用。本文结合当前电路教学实践,就密勒定理表述、证明及其应用作进一步的讨论。通过举例说明了密勒定理的应用,给出了密勒定理的教学建议。作为电路规律的一种总结,利用密勒定理分析电路时具有事半功倍的作用,可加深学生对电路本质的理解。本文的讨论可供从事电路教学的教师参考。

密勒定理;电路教学;电路分析

0 引言

电路定理是电路规律的总结。利用电路定理可简化对电路的分析,起到事半功倍的作用。因此,电路定理是电路教学中的重要教学内容。在所有的电路教材中,都有常用电路定理的介绍,如叠加定理、戴维宁定理等,但也有一些电路定理在电路后续课程如“模拟电子技术”课程中常常用到,而在“电路理论”或“电路分析”课程中并未加以介绍。密勒定理就是其中之一。笔者在教学中发现,在电子电路类课程中往往直接利用密勒定理对电路进行分析或设计[1],而没有对其进行表述或证明,而且应用密勒定理分析电路也有欠严密之处。这样就出现了“电路理论”或“电路分析”课程中密勒定理不是教学内容,而在电路后续课程中又必须用到密勒定理的情况。

本文根据笔者的教学实践,就密勒定理及其应用作进一步的讨论,以供大家参考。

1 密勒定理的表述及其证明

密勒定理由M.Miller于1920年在研究真空电子三极管输入阻抗时提出的,也称为密勒效应,在电路教材具有多种表述形式[1-4]。其较为严谨的表述形式为如图1(a)所示任一具有n个节点的电路。设节点1和节点2的电压分别为u n1和u n2,如已知un2/un1=A,则图1(b)电路与图1(a)电路等效,其中R1=R/(1-A),R2=R/(1-1/A)。

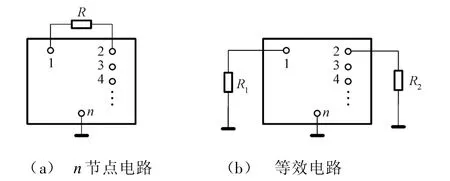
图1 密勒定理

文献[5]给出了密勒定理的一种证明,本文将给出另外一种证明。将如图1(a)所示电路等效为图2所示电路,且使其中节点电压u n(n+1)=0,则有

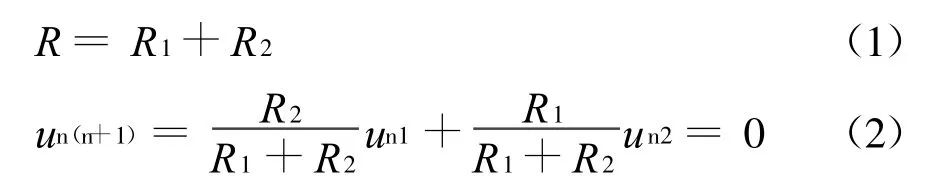
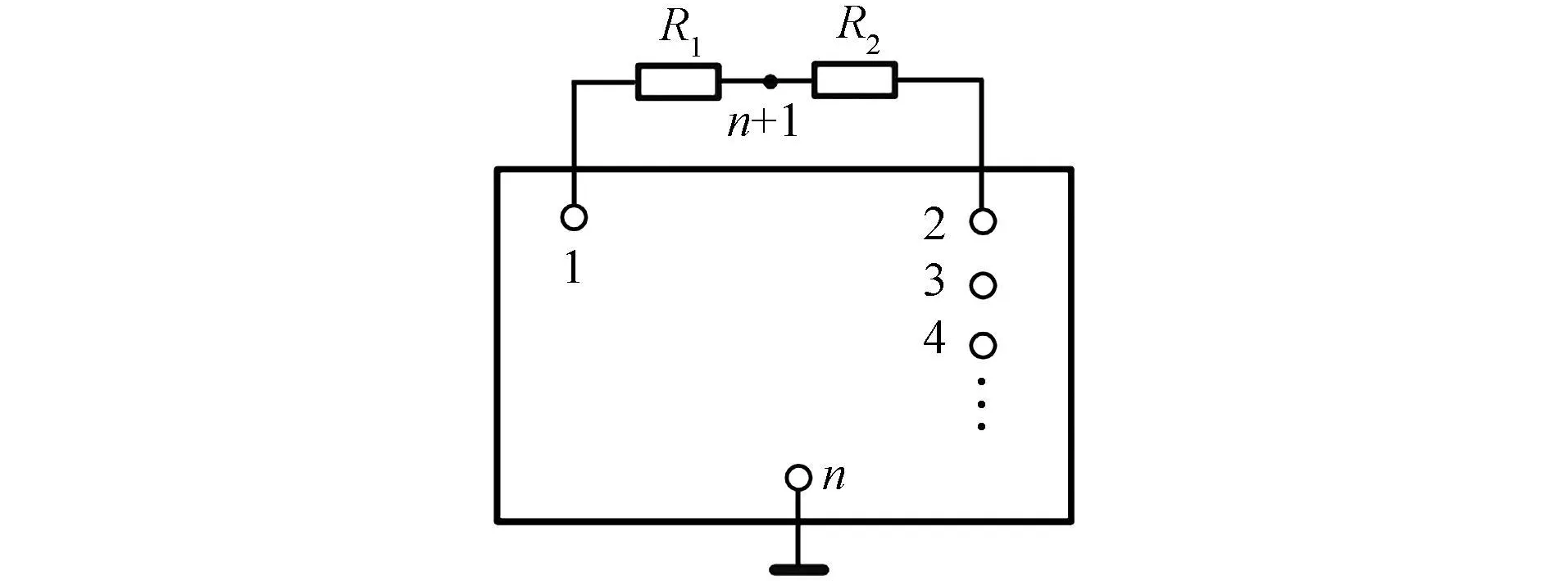
图2 密勒定理的证明

而图2所示电路与图1(b)所示电路等效,由此定理得证。

从密勒定理的表述中可以看出,对于具有支路连接的两个节点,如知道该两节点的电压,则利用密勒定理可消除两节点的支路连接关系,从而使得电路的分析过程得到简化。如果将图1(a)中的节点1看作输入节点,节点2看作输出节点,则利用密勒定理可简化输入、输出电阻的计算。

和其他电路定理类似,密勒定理在相量域或拉普拉斯变换域中都有相应的表现形式。

2 密勒定理的应用

密勒定理在电路分析中具有广泛的应用,下面通过例子加以说明。

[例1]如图3(a)所示电路,试求电压u。

图3 例1电路与等效电路

解本例可采用T-Π等效变换法或节点法或回路法求解,这里采用密勒定理求解。取电压源的负极为参考节点,由密勒定理,u n1=1V,u n2=u,A=u,从而可得到图3(b)所示等效电路,由KCL可得

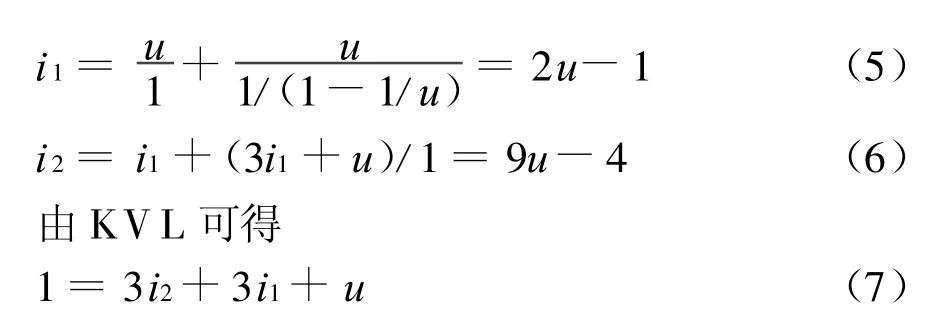
将式(5)、式(6)代入式(7),可解得u=8V/17,与采用其他方法得到的结果相同。

由例1可见,即使节点电压未知,也可采用密勒定理对电路进行分析。

[例2]试求图4(a)所示电路的电压比 H=u o/u S,设运算放大器的开环增益为 A,输入电阻为无穷大,输出电阻为零[6]。

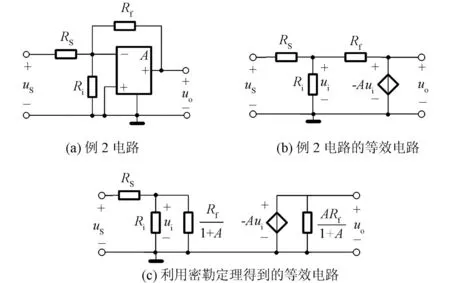
图4 例2电路与等效电路

解首先画出图4(a)所示电路的等效电路如图4(b)所示,再由密勒定理可得图4(c)所示等效电路。由图4(c)可得

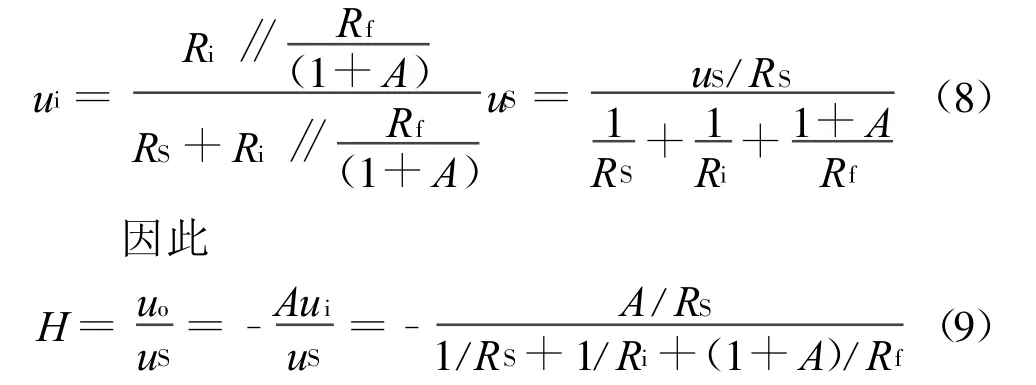
用其他方法分析例2电路都不如采用密勒定理来得简洁。

[例3]图5(a)所示为一电容倍增电路。试求输入端口的等效电路。

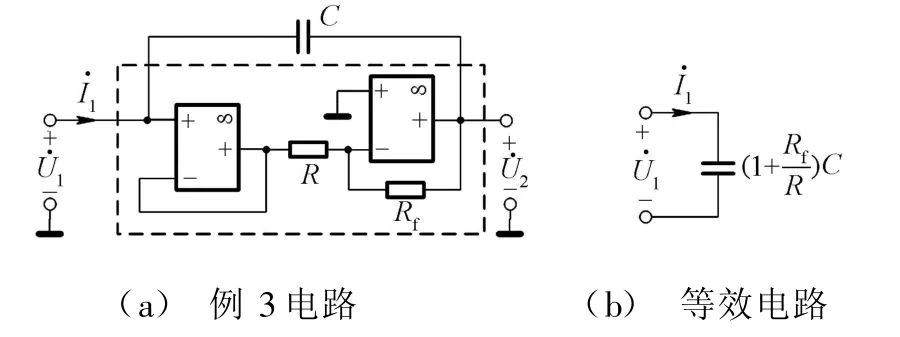
图5 例3电路与等效电路

解由图5(a)电路可知,电容两端的电压相量之比为A=﹒U2/﹒U1=1×(-Rf/R)=-Rf/R。再由密勒定理可知,电容支路等效于在输入端跨接一个(1+R f/R)C的电容,在输出端跨接(1+R f/R)C的电容。利用理想运算放大器的“虚断”特性,可得出输入端的等效电路如图5(b)所示。

3 结语

密勒定理在电路分析和设计中具有较广泛的应用,鉴于该定理在当前电路教学中的实际和笔者结合教学实践认为,可在电路教学中适当介绍密勒定理及其应用。其理由在于:①密勒定理的内容十分简洁,在理解上十分方便,作为电路教学内容不会占用过多学时;②存在相当多的电路问题可借助密勒定理来加以分析,其应用范围较为广泛;③作为电路规律的一种总结,利用密勒定理分析电路时具有事半功倍的作用,可加深学生对电路本质的理解,同时也可提高学生学习电路课程的兴趣。

本文通过举例说明了密勒定理在电路分析中的应用。其实,密勒定理在电路分析中还有更广泛的应用,如在理想微分电路、电容补偿、电阻补偿和滤波器电路等方面,由于篇幅所限,不再赘述。笔者相信,随着对密勒定理的进一步深入研究,肯定会挖掘出密勒定理在电路中的更有意义的价值。

[1] John M.M iller.Dependenceof the input impedan ce of a threeelectrode vacuum tube upon the load in the platecircuit.Scientific Papers of the Bu reau of Standards.1920,15(351):367-385

[2] 童诗白,华成英.模拟电子技术基础[M].北京:高等教育出版社.2001

[3] 李瀚荪.简明电路分析基础[M].北京:高等教育出版社.2002

[4] 李刚,林凌.电路学习与分析实例解析[M].北京:电子工业出版社.2008

[5] 李瀚荪,吴锡龙.简明电路分析基础教学指导书[M].北京:高等教育出版社.2003

[6] 陈洪亮,张峰,田社平.电路基础[M].北京:高等教育出版社.2007

Miller Theorem and Its Application

TIAN She-ping,CHEN Hong-liang

(Schoolo f E lectrica l and E lectronic Eng.,Shanghai Jiao Tong Univ.,Shangha i 200240,China)

Miller theorem has extensive app lication on circuit analysis and design.In consideration of present circuit teaching,the descrip tion and proo f of M iller theorem are discussed and app lication examp les about M iller theorem are introduced.Teaching suggestions are also given.M iller theorem has summ arized the circuits'law and can be app lied to analyzed circuits effectively.It is helpful for deepening students'understanding of circuits,enhancing ability of research and interests of learning.The discussion is helpfu l for the teaching of circuit.

miller theorem;circuit teaching;circuit analysis

TM 13

A

1008-0686(2011)02-0029-03

2010-09-04;

2010-11-30

田社平(1967-),男,博士,副教授,主要从事电路理论和动态检测技术的教学和科研工作,E-mail:sptian@sjtu.edu.cn